数学思维美的特征分析与教学思考

王福忠

（福州第四中学，福建 福州 350009）

所谓数学美感，主要是指因领悟到某种数学对象的内在实质而产生的愉悦感、满足感等。相应地，能使人产生这种美感的数学对象就称其具有数学美。［1］数学外在的形式能给人美感，如简单、对称、和谐、奇异，这些都是数学外在形式美的存在。数学思维的过程也能给人愉悦和满足感，这种数学思维活动给人的美就是思维之美，是一种数学的内在美。数学工作者通过数学思维活动，应用思维策略和已有数学理论，解决数学问题，得到新的数学理论，用数学语言表达思维结果，这是一个发现和创造的过程。数学的美好体验是伴随思维活动过程而产生的。

一、引发美感的数学思维活动的特点

在数学思维活动有时能给人带来美感，有时则不能给人带来美感。数学思维活动中思维美感产生往往是以对思维过程的认知为基础，在思维活动中或对思维过程的反思中产生。所以，能引发美感的数学思维活动具有一定的特点。

1.创造性

数学审美是一个实践的过程，数学家能深刻地感受到数学美，不仅是因为自然宇宙存在着美，更重要的是因为数学家创造心理中存在着灵感、顿悟、自由的心境和深邃的思想。［2］数学思维美体现了数学家的思想创造，它突破常规，或者突破原有思想，产生了认识和解决问题的新思想。如高斯计算“1+2+...+100”的和，按照常规的想法，是按从左到右的运算法则，两个数相加，加99次得到结果。而高斯突破常规，找到其中的规律，很快得到计算结果。这种突破常规的思维自然会给人美感体验。

2.发散性

发散思维是创造思维的主要成分，其主要特点表现在求异、奇特、想象丰富和不寻常规。徐利治先生给出这样一个公式：创造力=知识+发散思维能力。［3］发散思维意味着多角度联想，多方向尝试，多维度思考，发散思维能够揭示数学内部的奇妙联系，从而给人美感。如正弦定理的推导过程，可以用三角形法、辅助圆法、向量法等不同方法进行推导，三种方法体现了构建边角关系的三种不同路径。第一种方法通过作垂线转化为直角三角形，利用边相等构造等量关系；第二种方法，利用辅助圆构造直角三角形，通过直径相等构造等量关系；第三种方法通过向量和的三角形运算法则与向量数量积运算构造了一个等量关系。在思维发散中，学习者能体验到多彩多姿的创造思维的火花，产生愉悦感和满足感。

3.逻辑性

数学是一个有序的统一的整体，数学思维活动是按照某种逻辑进行的有序活动。著名数学家庞加莱曾就一个解答、一个证明之所以优美的原因简单地概括为一句话，那就是井然有序、统一协调。［4］合乎逻辑的有序的思维能给人美感。合乎认识逻辑的符号应用能给人美感，如用i表示虚数单位。解决数列求和问题本质在于分析项的结构，以实现和式的化简为目标，在这个思维统领下，所有的求和问题都纳入一个统一的整体。解决数列求和问题能给人美感，源于一般思考方法引导下思维具有的逻辑性。数学思想方法的应用能给人带来美感，因为数学思想方法强化了问题分析的逻辑性。

二、关于教学中引导学生感受数学思维美的问题思考

1.让学生经历发现与创造过程

心理学家告诉我们:在人的心理深处，都有一种根深蒂固的需求，那就是希望自己有朝一日成为一个发现者或探索者。［5］教师要努力创设和选择有利于思维创造性发挥的问题，引导学生独立思考，互相交流，留给学生足够的时间和思考的空间，让学生自己发现规律，寻找到解决问题的方法，享受发现和创造的喜悦，从中体验创造之美。如，在已知椭圆与直线相交弦的中点坐标求直线的斜率问题中，常规的思考是设直线方程，联立直线与椭圆的方程，利用中点坐标建立关于斜率的方程求斜率。这种常规的思维不能给学生带来解决问题的喜悦感。在学生完成这个常规的解答后，教师可以引导学生，还有什么解法？进一步引导学生提出问题，斜率与中点有怎样的关系？留出足够时间让学生自己去发现，当学生发现利用点代入椭圆方程，两方程相减，进而得到中点与斜率的内在关系时，喜悦感油然而生。

2.培养学生发散思维的习惯

在解题教学中，选择方法多样的数学问题，让学生能够有多种选择，引导学生经历从多个角度去分析问题，通过解题后的比较取得问题的最优解答的过程。引导学生解答问题时不满足于得到数学问题的答案，要在解题后的反思中进一步认识问题的结构，做好解题后的分析，在思维的发散点尝试新的解题思路。在发散思考中，让学生经历从解题念头产生，到付诸实施，到解决问题，丰富思维经验，增强思维的韧性，树立克服困难的自信，进而获得思维美的体验。

例：函数f(x)=aex-1-1-exln(x-1)存在零点x0，且x0＞ 1，则a的取值范围是（ ）。

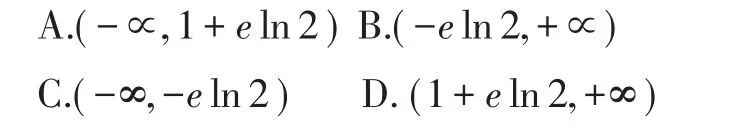
分析：零点可以看成函数图象与轴的交点的横坐标，也可以看成两个函数图象的交点的横坐标。

解 法 1：由 aex-1-1-exln(x+1)=0，得 aex-1=exln(x+1)+1，

结合图象得a＞eln2+1.

解法 2：由aex-1-1-exln(x+1)=0，得 ln(x+1)结合图象得a＞eln2+1学生在分析问题时比较自然会考虑参变分离，通过研究函数性质与图象得到结果。教师应引导学生进一步探究，得到解法2。教师还可以利用几何作图软件作出的图象和h(x)=ln(x+1)的图象，让学生观察到一个图象是定的，另一个图象是动的，从而体会构造函数的方法。

3.帮助学生理解思维逻辑

数学内部是一个有序的结构，数学思维的过程必然遵循一定的逻辑关系与推理方法。帮助学生理解数学发现、问题解决的逻辑，有助于学生顺利建构知识，习得解决问题的方法，提高解决问题的能力，从而获得正向的情感体验，形成积极的价值判断。

教学中加入必要的历史知识能帮助学生理解知识形成的内在逻辑。虚数单位为什么用字母表示，如果不向学生解释，当然学生也能记住并使用。但是，如果从让学生体验数学美，更好理解数学出发进行教学，就必须要简单介绍相关历史背景。我们知道，人们认为虚数是想象出来的数，在英语里翻译为Imaginary，取这个英语单词的首字母，就有了用来表示虚数单位。这样的教学就让学生理解了符号表示的内在思维逻辑，稍加反思，思维美油然而生。

数学思维的结果在表达上常常不能反映思考的全过程，也不能反映思考的先后顺序。比如，函数问题中参数的讨论，对参数的分类，在结果表达中，虽然是先写参数的不同取值，然后再讨论在不同取值下的结果，但是思维过程刚好是反的。在教学中，要注意还原思考过程的本来面目，揭示结果的来龙去脉，促进学生的理解。