钢管混凝土格构式新型风力发电机塔架风振响应

2018-08-30文昊天高春彦

噪声与振动控制 2018年4期

李斌，文昊天，高春彦

（内蒙古科技大学土木工程学院土木工程系，内蒙古包头 014010）

风力发电单机容量的不断增大使得应用于大型风电机组的传统塔架结构安全性越来越低[1]，风电事故时有发生。当风力发电机塔筒超过一定高度后，其结构的力学性能下降非常明显，主要表现在：塔顶在水平荷载作用下变形过大，塔身与上部风机产生共振，塔身容易发生疲劳破坏[2]。塔架是风力发电机组的主要承载结构，不但要承受机舱重量、风轮作用力以及风对塔架的弯、剪、扭等静力作用，还要承受振动作用力[3]。而且钢制高耸结构对局部缺陷十分敏感，其临界承载力只能达到理论值的1/5～1/3，很容易发生失稳破坏[4]。塔架是为风力发电机组正常工作服务的结构，其发展水平应与风力发电机组的发展相协调。为了满足现代风力发电机的工作需求，必须要保证塔架在风荷载作用下的安全。

根据各国风机受损的历史统计数据，塔架是风机受损部件中遭受破坏比率较大的部件之一，占到19%[5]。从功能性角度来看，塔架是风电机组中重要的支撑结构，为风力发电机提供必要的工作高度；从荷载角度来看，塔架的重量占到风机总重的1/2左右；从经济性角度来看，塔架的成本大约为整个风机制造总成本的15%左右，而且塔架倒塌必定造成风力发电机的损伤[6]。因此，钢管混凝土格构式风力发电机塔架在风荷载作用下动力响应的研究对于提高塔架的设计水准、保证风机的运行安全和整机性能都有重要意义。

1 风速时程模拟

对本文所采用的钢管混凝土格构式风力发电机塔架不同高度处的13个计算点进行风速时程模拟，计算点位置选取如图1所示。

图1 塔架横截面与计算点位置示意图

其中13号节点为风轮中心位置。选取我国规范所采用的Davenport脉动水平风速谱以及Shiotami的简化空间相关性系数表达式。为了得到较为准确的脉动风速时程曲线，采用谐波合成法对塔架工作地区的脉动风进行风速时程模拟；为了得到更准确的平均风速，以对数律求解平均风速廓线。具体模拟参数如表1所示。

表1 风速时程模拟参数

借助MATLAB软件编写程序，最终生成各计算点的风速时程曲线。

2 风力发电机塔架有限元模型建立

本文所采用的2 MW风力发电机塔架高度为60 m，风机转子中心高度为61.5 m。塔架分12层，层高有4 m、5 m和6 m三种。应用ABAQUS软件建立钢管混凝土格构式风力发电机塔架有限元模型，钢管模型采用壳单元，混凝土模型采用实体单元。将钢管与混凝土的接触定义为刚体约束，忽略钢管与混凝土在受力过程中的局部滑移。将所有焊接节点设置为绑定约束，另外忽略风力发电机塔架的基础与地基土之间复杂的相互作用，将之视为刚性连接。为了提高网格质量，对装配件整体布种，对不同单元分别指派网格控制属性。在分析步中设置频率分析步，提取塔架的各阶频率和振型，用于后续风振响应计算。

图2 风力发电机塔架有限元模型

3 风力发电机塔架风致响应分析

由模拟得到的各个计算点风速时程曲线求解对应的风荷载时程曲线，利用ABAQUS有限元软件将风荷载以节点力的形式作用于塔架模型对应的计算点，分析得到钢管混凝土格构式风力发电机塔架各计算点的位移、速度和加速度响应曲线。

3.1 塔架风轮中心位置处的风振响应

提取风轮中心位置处的位移、速度和加速度响应时程曲线分别如图3、图4、图5所示。

图3 13号节点位移响应时程曲线

图4 13号节点速度响应时程曲线

图5 13号节点加速度响应时程曲线

从图3可以看出，塔架风轮中心位置处的顺风向位移在0.07 m～0.23 m之间，位移响应峰值为0.23 m，平衡位置与初始位置的水平距离约为0.17 m，在模拟的时段内13号节点位置处的位移响应表现出很强的随机性。

由图4可知13号节点的速度响应在±0.06 m/s之间，大部分时间处于±0.02 m/s之间，速度峰值响应为0.06 m/s。

由图5可知，风轮中心位置处加速度峰值响应为0.11 m/s2，同样也表现出极强的随机性和波动性。

3.2 塔架整体风振响应

从表2可以看出随着高度的增加，结构的位移响应均值、位移响应极值以及加速度响应均方差都在增加。

位移响应极值与位移响应均值的差距逐渐增大，脉动风对结构位移响应的作用是随高度不断增加的。在61.5 m高度处脉动风位移响应分量已接近总风响应的30%。

图6、图7所示分别为钢管混凝土格构式风力发电机塔架各节点位移的响应均值和加速度响应的均方差随塔架高度变化的关系。

从图中可以看出位移响应均值和加速度响应均方差随高度的增加逐渐变大，且变化速度越来越快。这主要是因为随着高度的增加结构的横截面面积减小、刚度下降而荷载反而增大所引起的。

图6 塔架位移响应均值

图7 塔架加速度响应均方差

为了研究不同风速工况下钢管混凝土格构式风力发电机塔架的风振响应，在不改变其他参数的条件条件下，分别取vˉ10=10 m/s、20 m/s、25 m/s、30 m/s对塔架的8号节点和13号节点进行风振响应计算。

图8中就风力发电机塔架8号节点和13号节点在不同风速工况下的加速度响应均方差进行了比较。从图中可以看出节点的风振响应随着基本风速的增加单调增加。节点加速度响应均方差在10 m/s～20 m/s的风速范围内增长较为缓慢，在20 m/s～25 m/s的风速范围内增速明显增大，之后又有所下降。相比之下，高度越高，风振响应对风速的变化越敏感。

图8 不同风速工况下节点加速度响应均方差

不同结构形式的阻尼比取值不同，阻尼比会影响动力时程计算的结果。为了分析不同阻尼比对塔架风振响应的影响，取基本风速其他参数保持不变，分别取阻尼比ζ=0.02、0.035、0.05，计算塔架8号节点与13号节点的加速度响应时程。

由图9可以看出，节点的风振响应随着阻尼比的增大而减小。在钢管中灌入混凝土可以提高结构的阻尼比，在一定程度上达到减振的目的。

图9 不同阻尼比时节点加速度响应均方差

4 塔架顺风向风振系数

4.1 塔架结构分段

本文研究的钢管混凝土格构式风力发电机塔架为高耸结构，为保证准确性，对风振系数的分析和计算必须分段进行。

如图10所示，将钢管混凝土格构式风力发电机塔架沿高度方向分为6段。

各塔段结构参数如表2所示，其中迎风面宽度为各塔段二分之一高度处的迎风面宽度。

4.2 不同方法中的风振系数计算

计算所选参数见表3至表7。

图10 塔架分段图

4.3 结果分析

将上一节中按照四种不同方法计算得到的风振系数进行比较，见图11。

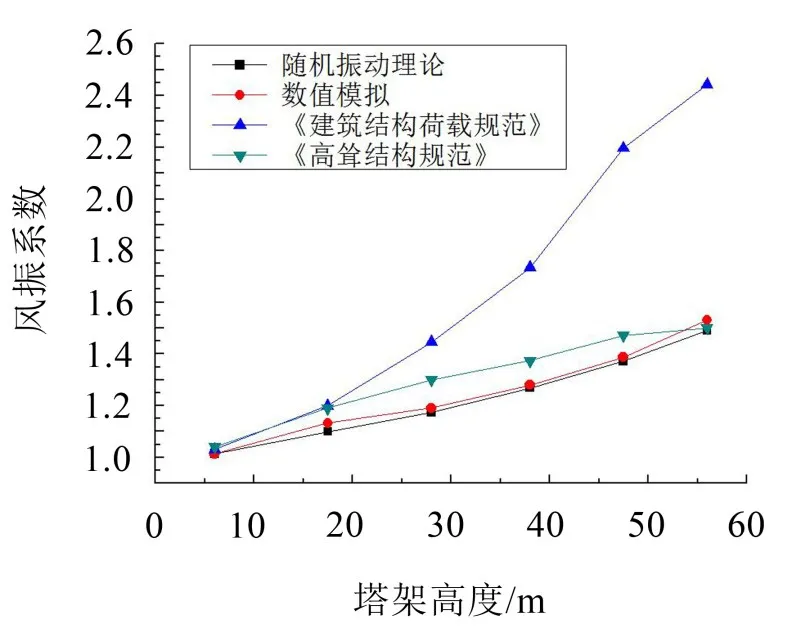
图11 不同方法计算所得的风振系数对比

从图中可以看出，基于随机振动理论按Davenport谱和按时程分析结果所得到的风振系数基本吻合。在按随机振动理论计算塔架响应时只取了第1阶振型，这表明基于随机振动理论计算钢管混凝土格构式风力发电机塔架风振系数只取第1阶振型进行计算是可行的。因为只取了起控制作用的第1阶振型，随机振动理论的计算值较数值模拟结果略微偏低。

表3 钢管混凝土格构式风力发电机塔架各塔段结构参数

表4 基于Davenport风谱计算所得的风电塔架风振系数

表5 基于《建筑结构荷载规范》（GB50009-2012）计算所得的风电塔架风振系数

表6 基于《高耸结构设计规范》（GB50135-2006）计算所得的风电塔架风振系数

表7 基于数值分析结果计算所得的风振系数

按照《高耸结构设计规范》（GB50135-2006）计算所得的风振系数与数值模拟的结果相比较，在50 m以下尚可，超过50 m以后出现了偏低的情况，这对结构的安全性是不利的。现行《高耸结构设计规范》（GB50135-2006）计算参数少，计算便利，但参数的物理意义不够明确，且针对不同结构形式的参数选用描述模糊、不够全面，在确定系数时往往需要自行插值计算，受主观影响较大。

按照《建筑结构荷载规范》（GB50009-2012）计算所得的风振系数与数值模拟的结果吻合度最差。新版《建筑结构荷载规范》（GB50009-2012）关于风振系数计算的参数设置较为详细，每个参数的物理意义清晰，但对于钢管混凝土格构式风力发电机塔架这种结构形式来说计算结果过于保守，并不十分适用。