一道美国数学奥林匹克题的另证
2018-08-30湖南师范大学数学与统计学院410081
中学数学研究(江西) 2018年8期
湖南师范大学数学与统计学院 (410081) 张 卫 吴 乐
原题ΔABC具有下面性质:存在一个内部的点P使得∠PAB=10°,∠PBA=20°,∠PCA=30°,∠PAC=40°.证明:ΔABC是等腰三角形.
此题来源于第25届USAMO,文[1]给出了此题的几何解法.原解法是通过构造一系列辅助线来完成的,这种解法对考生的解题技巧以及思维能力有很高的要求,一般的学生很难想到此方法.本人结合题目的特点,利用三角函数的知识,给出了此题一个很自然的解法.
下面给出此题的三角函数证明方法.
证明:记∠PBC=α,∠PCB=β,PA=a′,PB=b′,PC=c′.

另一方面,在ΔABC中,又有
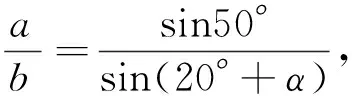
故由②和③可得sin(20°+α)sin40°sin100°=sinαsin110°sin50°.④
反复利用积化和差公式以及余角公式,可最终将④式化为sinαsin10°+cosαsin80°+sinαsin50°-cosαsin40°=sinαcos60°-cosαsin60°+sinαsin70°+cosαsin20°⑤
整理得sinα(sin10°+sin50°)+cosα(sin80°-sin40°)=sinαsin70°+cosαsin20°+sin(α-60°).⑥
再注意到上式中角与角之间的关系,可在①式中取θ1、θ2为适当的值得到如下关系式
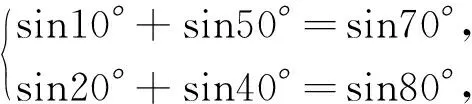
代入⑥,进一步化简成sin(α-60°)=0.
由于α∈(0,180°),所以α=60°,β=180°-∠BPC-α=20°,继而有∠C=50°=∠A,BA=BC,得证.
评注:上述解法充分考虑了题目的特点,利用三角函数中积化和差等知识,推出三角形中存在两内角相等,比原解法更容易上手.
