两类导数证明题型方法探究
2018-08-30江苏省常熟外国语学校215500剑江苏省常熟市中学215500吴旭红
江苏省常熟外国语学校 (215500) 丁 剑江苏省常熟市中学 (215500) 吴旭红
在导函数复习和测试的过程中,有两类导数证明题学生在处理上有一定的困难,本文针对这两种题型,进行剖析,归纳出解题的一般方法,供同行和学生参考学习.
题型一用已知函数单调性证明
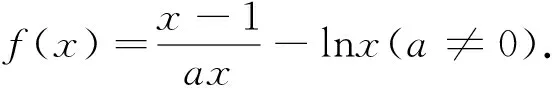
(1)求函数f(x)的单调区间;
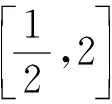


例2 2017-2018学年第一学期高三期中调研23(2017.11)
(1)若不等式(x+1)ln(x+1)≥ax对任意x∈[0,+∞)恒成立,求实数a的取值范围;

解析:(1)易求得a≤1.


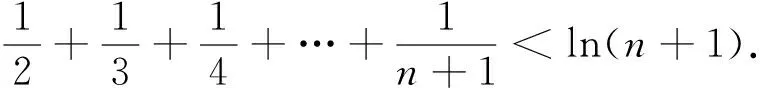
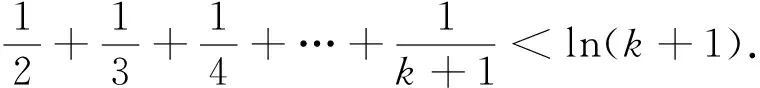

例3 已知函数f(x)=ex,g(x)=lnx+1(x≥1).
(1)求函数h(x)=f(x-1)-g(x)(x≥1)的最小值;
(2)已知1≤y

(2)由(1)可知,当x≥1时,h(x)=ex-1-lnx-1≥0,∵1≤y ∵1≤y 剖析:此类证明基本使用前一问的条件,赋值,满足范围即有单调性,则可以用上一问结论.例1若没有第二问铺垫,直接证第三问,可能加深难度.例2测试时利用第一问结论进行论证的不多,少部分同学按法1用裂项完成,极少数移项构造数列根据单调性证明.例3两次利用前面的结论,结合了不等式的递推性质证得. 题型二与两个零点相关不等式型的证明 例4 (不含字母指数型)过点P(-1,0)作曲线f(x)=ex的切线l. (1)求切线l的方程;(x-y+1=0) 设f(x)=(x+1)ex,则f(x1)=f(x2).f′(x)=(x+2)ex,当x<-2时,f′(x)<0,当x>-2时,f′(x)>0; ∴f(x)在(-∞,-2]上单调递减,在[-2,+∞)单调递增. ∵x1≠x2,不妨设x1<-2,x2>-2. 设g(x)=f(x)-f(-4-x),则g′(x)=f′(x)+f′(-4-x)=(x+2)ex(1-e-2(2+x)),当x>-2时,g′(x)>0,g(x)在(-2,+∞)单调递增,∴g(x)>g(-2)=0,即当x>-2时,f(x)>f(-4-x).∵x2>-2,∴f(x2)>f(-4-x2),则f(x1)>f(-4-x2).∵x1<-2,x2>-2,∴-4-x2<-2,且f(x)在(-∞,-2)单调递减,∴x1<-4-x2,即x1+x2<-4. 例5 (含字母指数型)已知函数f(x)=(x-k-1)ex(e为自然对数的底数,e≈2.71828,k∈R). (1)当x>0时,求f(x)的单调区间和极值; (2)①若对于任意x∈[1,2],都有f(x)<4x成立,求k的取值范围; ②若x1≠x2,且f(x1)=f(x2),证明:x1+x2<2k. 解:(1)(2)①略. ②由已知f(x1)=f(x2)(x1≠x2),结合(1)可知k>0,f(x)在(-∞,k)上单调递减,在(k,+∞)上单调递增,又f(k+1)=0,∴x 例6 (不含字母对数型).常熟市2018届高三阶段性抽测二(2017.12) ∵x1>x2,∴x1∈(1,+∞),x2∈(0,1), ∴2-x2∈(1,+∞). ∵x2∈(0,1),∴f(2-x2) ∴x1+x2>2. 例7 (含字母对数型1)苏州市2017届高三调研测试(2017.01) 已知函数f(x)=(lnx-k-1)x(k∈R). (1)当x>1时,求f(x)的单调区间和极值;(当k≤0时增区间是(1,+∞),无单调递减区间,无极值;当k>0时,减区间(1,ek),增区间(ek,+∞),极小值f(ek)=-ek,无极大值.) (3)若x1≠x2,且f(x1)=f(x2),证明:x1x2 解析:(3)(法1)因为f(x1)=f(x2),由(1)知,函数f(x)在区间(0,ek)上单调递减,在区间(ek,+∞)上单调递增,且f(ek+1)=0. (法2)要证x1x2 例8 (含字母对数型2)已知函数f(x)=x-alnx(x∈R+),a为实数,若f(x)有两个零点x1,x2且x1 解析:(1)、(2)略.(3)(法1)f(x1)=x1-alnx1=0①,f(x2)=x2-alnx2=0②,①+②,得x1+x2=alnx1+alnx2=alnx1x2. 要证x1·x2>e2,只要证x1+x2>2a,即证x2>2a-x1. 由(1)f(x)在(0,a)上单调递减,在(a,+∞)上单调递增.又x1 ∴x2·x1>e2. ∴x2·x1>e2. 例8的法1通过分析法书写,取对数后转换成和式,构造差式函数(不妨称之为极值点构造法)处理,法2更为明晰,用已知零点所得等式,加减后处理,消去a,然后类似例7的法2换元证得,这里需要一定的转化技巧.教学时可通过范例,让学生深谙其解法,并灵活运用之. 结语:本文两类导数证明题属于难度较大的题,需要了解其本质:题型一用原函数单调性,赋值处理;题型二分为两类解法,极值点构造法和换元求导法.
(一)和型



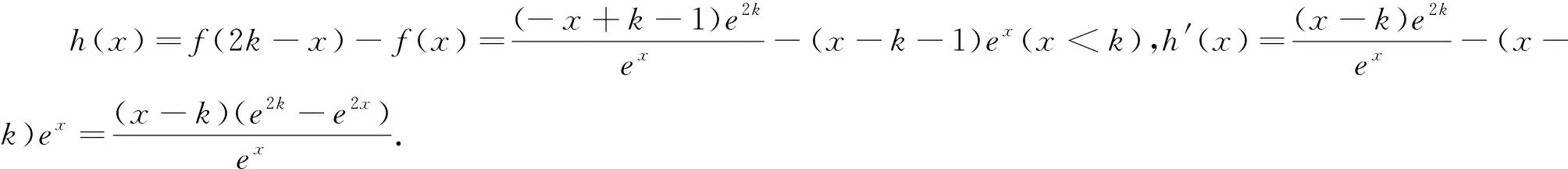
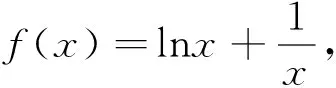
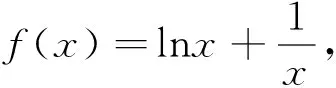

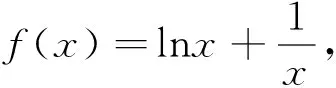


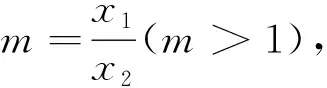




(二)积型