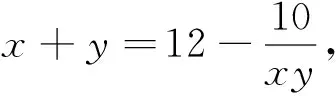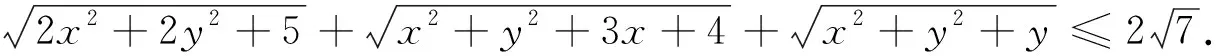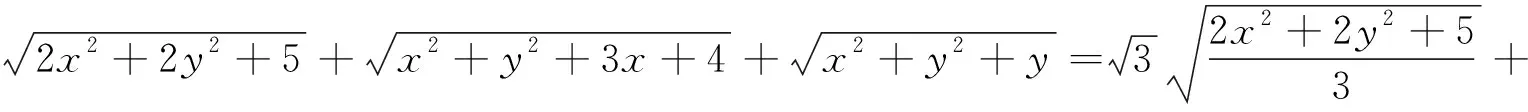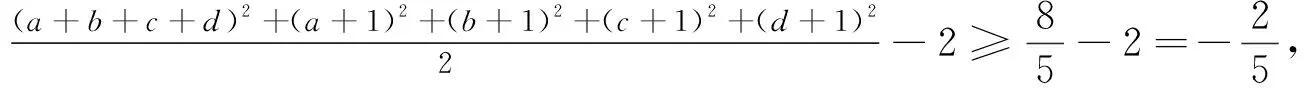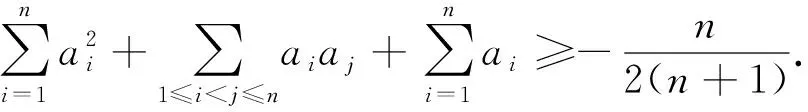若干2018年国内外数学奥林匹克不等式题的精彩证明

南昌大学附属中学 (330047) 陈一君

例1 (2018年哈萨克斯坦数学奥林匹克)已知a,b,c,d∈(0,1)，求证：(ab-cd)(ac+bd)(ad-bc)+min{a,b,c,d}<1.

证明：不妨设x=min{a,b,c,d}，则(ab-cd)(ac+bd)(ad-bc)+min{a,b,c,d}=(bd(a2+c2)-ac(b2+d2))(ac+bd)+x≤bd(a-c)2(ac+bd)+x≤(a-c)2(ac+bd)+x≤(1-x)2(ac+bd)+x≤(1-x)2(1+x)+x=1-(1-x)x2<1.

注1：减元是解答此题的核心.

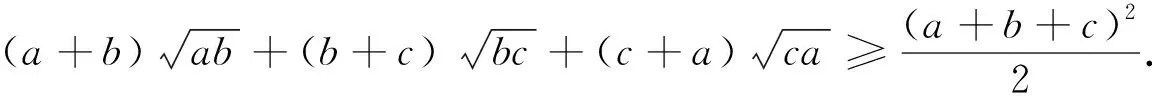
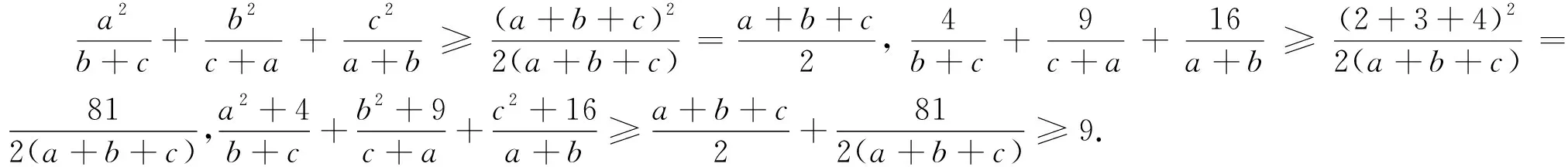
注3：例2、例3中都是严格不等式.同样可证：

例4 (2018年罗马尼亚数学奥林匹克)已知1

(xy-1)(xy-10)2≥0，综上，原不等式成立.

注4：去对数、减元等等，都是我们解题教学中的口头禅.

例7 (2018年上海高中数学竞赛)设a,b,c,d是实数，求a2+b2+c2+d2+ab+ac+ad+bc+bd+cd+a+b+c+d的最小值.

解：由柯西不等式，可得[(a+b+c+d)2+(a+1)2+(b+1)2+(c+1)2+(d+1)2](1+1+1+1+1)≥(a+b+c+d-a-b-c-d-4)2=16，a2+b2+c2+d2+ab+ac+ad+bc+bd+cd+a+b+c+d=

注7：考虑问题的一般情形，笔者得到(证明从略)：