高精密机床进给系统模型降阶技术*
2018-08-29华青松张洪信程联军赵清海毛新凯
宣 贺,华青松,张洪信,程联军,赵清海,毛新凯
(青岛大学 a.机电工程学院;b.动力集成及储能系统工程技术中心,山东 青岛 266071)
0 引言
机床工业是我国加工制造业的根本。机床工作时振动可产生较大的误差,机床的模型降阶可以减小振动,提高机床的生产效率。
高精密机床的结构复杂度越高,分析时的时间和费用增加的越快。这就需要对高精密机床的结构进行降阶,进几年,动力缩减技术被广泛应用到模型的降阶研究和相关领域,在振动分析中具有特别重大的意义[1-2]。
动力减缩技术模型降阶主要包括两类:①整体降阶法,包括动力缩聚,模态法、Lanozos等法。②局部降阶法,包括动态子结构法或模态综合法[3-4]。控制理论中的降阶方法主要有:平衡降阶法(Balanced Reduction)、代价分析法(Cost Analysis)、最优投影法(Optimal Projection),但是这些方法对于降低维数过高的机床模型的阶数有一定的困难。因此,本文应用动态子结构法,即对于复杂结构的动力学模型,首先对物理空间模型降阶,然后与物理模型和平衡降阶法联系起来,得到的降阶模型不仅阶数低,而且所得状态空间方程具有可观性和可控性,这样就能保证控制器的设计与分析。
1 动态子结构降阶法
动态子结构降阶技术把主自由度分为自由度和副自由度,利用主、副自由度之间的动力缩聚矩阵把原系统的刚度矩阵,阻尼矩阵和质量矩阵投影到一个只有主自由度的物理空间中[5]。从数学角度上看,动态子结构降阶法是一种物理变换,降阶后的模型仍在物理空间。
如图1所示,为了对机床实时进给位置进行建模,需要在进给部件柔性体1和2之间实时定义联接单元,并删除前一时间点已建立的联接单元,以获得该位置的多体耦合模型。柔性体之间联接单元的生成和删除通过编程实现,最重要的是快速搜寻所需的联接单元节点。常用联接单元是弹簧——阻尼单元[6-7]。采用这种单元联接两个自由子结构时,要求1、2自由子结构上节点的位置、序号一一对应,这给有限元网格划分提出了很高的要求;如果接合面上节点单元比较多,并且是非等距分布,则无法通过节点生成联接单元[8]。同时,如果接合面上节点数目很大,则寻找联接单元节点的所需时间会很长,导致系统耦合建模时间过长,不能满足高效建模的要求。

图1 采用弹簧-阻尼链接单元联接的柔性体系统
本文将研究高效的节点搜寻域floor方法。将进给路线长度进行一维等距离划分,长度为最近两个节点之间的距离[9-10]。将等距的域按顺序生成一个向量,每个向量元素包含该域中的所有单元节点。实时域中序号为m的元素表达方式为:
(1)
xact表示进给装置(自由子结构2)在y方向上的实时位置,l为导轨(自由子结构)长度。建立实时位置xact的弹簧——阻尼联接单元时,直接选取该时间点离MASTER节点最近的对应域中的节点作为单元节点[11]。通过定义节点搜寻域的方法,避免了花很长时间找联接单元节点的问题,从而确保快速建模的要求。根据实际模型中机床结合部的实际情况,也可将节点搜寻域定义为二维、或者三维的向量,在公式(1) 中添加yact和zact即可。搜寻节点的算法等同于一维算法。
系统的结构动力学方程可用如下方程表示:

(2)
式中,M、C和K分别为机床进给系统的质量矩阵,阻尼矩阵和刚度矩阵,它们均以n×n阶对称矩阵,X为位移向量,F为结构受到的外作用力向量。把该结构的总自由度n分为主自由度m和副自由度两部分,则式(2)可用分块的形式表示为:
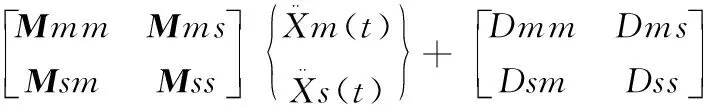
(3)
假定结构主、副自由度之间的关联矩阵为R,即:

(4)
关联矩阵R可由下式来解,
R=Kss-1[(Msm+MssR)MR-1KR-Ksm]
(5)
关联矩阵R包含了降阶模型的参数,而这些参数与关联矩阵R有关,因此常用迭代法求解,当引入迭代法后,经过(i)次迭代后降阶系统动力方程为:
(6)
其中,
MR(i)=Mmm+(R(i))TMsm+
MmsR(i)+(R(i))TMssR(i)
(7)
DR(i)=Dmm+(R(i))TDsm+
DmsR(i)+(R(i))TDssR(i)
(8)
KR(i)=Kmm+(R(i))TKsm+
KmsR(i)+(R(i))TKssR(i)
(9)
FR(i)(t)=Fm(t)+(R(i))TFs(t)
(10)
R的初始值R(0)=-Kss-1Ksm。
主自由度的选择和主自由度的多少对动态子结构降阶法尤为重要,因为它们直接影响到降阶方法的精度和适用范围[12-14]。一般而言,从定性的角度出发,应该遵循以下规则,①所选择的主自由度应该是质量阵中最大元素所对应的自由度,或是在所选的振动幅值中,幅值变化最大的自由度。②对简单结构而言,主自由度应选择线位移,而不是转角位移。③对复杂结构而言,应该是惯性和柔度均较大的区域。④从定量的角度出发,Matta和Shah直接选择m个对角元素的最小比值ri=kii/Mii所对应的自由度为主自由度。⑤对于主自由度的选择和多少,应该根据问题实际情况而定。
2 高精密机床进给系统降阶分析
在进行一般动力学仿真分析时,一些螺栓连接往往用固定副约束,但进行振动分析尤其想考虑振动通过螺栓连接进行传递时需要使用弹性连接描述部件间的运动关系。这时使用Adams/Vibration提供了两种阻尼器的连接方式,一种是FD阻尼器,另一种是FD 3D阻尼器,其中FD阻尼器只阻碍两个构件间在一个自由度上的相对运动,而FD 3D阻尼器可以同时阻碍两个构件在多个自由度上的相对运动。

图2 进给系统多体系统动力学模型
在ADAMS中对Adams/Vibration模块进行加载,然后进行如下操作。
输入通道:在进给系统模型中,主要考虑工作台上的零件在切削力的作用下所导致的进给系统的振动,所以在工作台的x方向上添加激励力。力的大小为600N,相位为0o、方向沿x轴的激励力。
输出通道:丝杠的振动是影响加工精度的一个至关重要的因素,所以输出通道选择丝杠上的中间点,以便更加细致入微的观察,故对丝杆的中间点定义的输出通道为z方向[15]。
3 降阶仿真分析
对进给系统进行振动分析,运行ADAMS/Vibration模块,点击Test,然后点击Vibration Analysis,在ADAMS中将丝杠的柔性体转换为刚性体,得到刚性体全模型丝杠上中点的幅频特性和相频特性[16]。然后在全模型的基础上添加FD 3D阻尼器,设置C1=0.006,K1=1.25,对其进行模型仿真,进入后处理模块,得到降阶模型丝杠中点的幅频特性和相频特性。图3是原始模型与降阶模型的幅频特性曲线,图4是原始模型与降阶模型的相频特性曲线。

图3 原始模型与降阶模型的幅频特性曲线

图4 原始模型与降阶模型的相频特性曲线
从图3和图4可以看出,在模型仿真运行中,降阶模型能够很好的逼近刚柔原始模型。平衡降阶模型基本上重现了原始模型的动态特性,既说明了柔性体的仿真准确性,又说明本文中动态子结构降阶法能够准确、可靠地实现主动约束层阻尼结构的动力学模型降阶[17]。在状态空间对原始模型进行子结构降阶。不仅能够降低模型阶数,而且所得状态空间方程可观且可控,这在振动主动控制中具有特别重要的意义。
对于二阶线性系统(a,b,c,d),定义可控矩阵,可观矩阵如下:
根据以上公式可以得出,平衡降阶模型可控矩阵及可观矩阵的秩为16。当系统可控时,可控矩阵gc满秩;当系统可观时,可观矩阵go满秩[18],降阶模型即可控又可观,由于两次降阶后模型阶数很低,使得实时振动变主动控制成为可能。
在ADAMS仿真模型中,以丝杠的中点为研究对象,进行仿真分析,再转换为刚性体,进行仿真[19]。得到模型降阶前后的脉冲响应,如图6所示。表1反映的是降阶前后仿真计算时间对比。
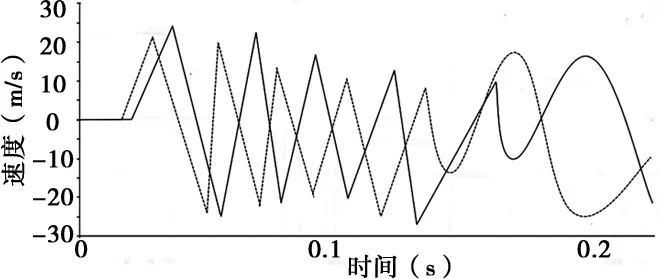
图5 丝杠中心速度时间历程

图6 模型降阶前后的脉冲响应

方法求解时间t/s效率比原始模型1201降阶模型85.81.39
通过图5、图6和表1可以看出,降阶模型和原始模型的计算结果吻合极好,从仿真计算时间上来看,模型降阶后的计算时间更短,降阶后模型的精确度更高,说明本文提出的降阶模型比全模型具有更高的计算效率和仿真精确效率。
4 结论
(1)提出在动态仿真软件ADAMS通过添加FD 3D阻尼器对机床进给系统模型进行降阶。
(2)通过动态子结构降阶法和ADAMS动态仿真分析,降阶后的幅频特性和脉冲响应极好地吻合,说明此降阶方法的准确性。
(3)降阶后机床进给系统模型的仿真精确效率更高。
(4)高精密机床进给系统降阶后的仿真计算时间更短,效率提高了39%。
