基于FTA-AHP的数控磨床主轴系统可靠性分析*

罗 静，陈一凡，张根保

(1.重庆理工大学 a.机械工程学院；b.汽车零部件先进制造技术教育部重点实验室，重庆 400054；2.重庆大学 机械工程学院，重庆 400044)

0 引言

主轴系统作为数控磨床加工的关键子系统，一旦出现故障，势必会影响磨削性能的稳定性，并且增加加工成本和维修时间，其中主轴系统可靠性一直是待解决的关键问题之一[1-2]。关于主轴系统可靠性研究方面国内外学者做了大量研究与分析，如谷东伟[3]采用故障总时间法对主轴现场试验数据进行预处理，从而建立了可靠性评估模型，最终准确得到了主轴系统可靠性评价指标。张义民[4]分析了主轴系统的动态特性，当主轴转速一定时，采用BP神经网络计算出主轴系统的可靠性及各随机参数的可靠性灵敏度。李兆军[5]利用有限元方法推导出单失效概率和联合失效概率计算公式，在此基础上，建立了主轴系统非线性振动可靠性模型及可靠性分析方法，最后使用Monte Carlo方法验证了其可行性。王广勇[6]采用FMECA分析对主轴系统进行故障分析，通过致命度分析确定了易出现故障的零部件，并提出改进措施。

目前国内针对主轴系统主要侧重于有限元分析研究[7-9]，对主轴系统可靠性分析与研究并不全面及深入，因此本文根据国内某企业收集到的主轴系统故障维修数据，建立电主轴失效故障树，确定了影响主轴系统失效的故障模式和原因，并结合层次分析法(AHP)建立了失效递阶模型，找出影响主轴系统的关键故障因素，并提出可靠性改善措施来提高其可靠性。

1 FTA分析

故障树分析就是把每个故障根源用逻辑关系串联起来，形成一棵倒立的树状分析图，以最不希望发生的故障作为顶事件出发，进而自上而下、逐层扩展至各个故障原因，然后再以各个故障原因作为顶事件，反复循环，直至不能再往下探明为止[10]。建树中用到的逻辑符号如表1所示。

表1 建树中涉及事件和逻辑符号

1.1 电主轴故障树分析

电主轴作为主轴系统的重要组成部分，其运行的稳定性直接关系被加工零件质量的好坏，因此在故障树中以电主轴失效作为顶事件，主要以发出异响、工作精度超差、报警、旋转异常四大典型故障模式对其展开故障树分析。分析结果如图1所示。

图1 电主轴故障树分析

上述故障树中对应的事件及具体内容如表2所示。

表2 电主轴故障树对应事件表

从表2可以发现，造成电主轴失效的故障模式总共有9个，分别是发出异响、工作精度超差、报警、旋转异常、运动部件抖动、温升过高、过流、无法转动及转位、移位无动作，它们之间属于逻辑或关系，只要任一事件的发生，都会直接导致顶事件发生。通过这些相应的中间事件又可以逐层往下寻找相应的中间事件和故障根源，最终把导致顶事件发生的所有故障根源挖掘出来。

2 基于FTA-AHP电主轴可靠性分析

FTA-AHP的主要思想是：将故障树分析的复杂结构层次模型简化，并引入测度理论对评价目标进行判断和比较，采用萨迪相对重要度对其量化，逐层次得到同一层次因素相对上一层次因素的判断矩阵，进而计算出权重值，最后对各个评价目标综合权重排序[11]。

通过前面的故障树分析确定了影响电主轴故障的各影响因素，单从故障发生率是不能够合理、准确的抉择哪些属于关键故障因素，因此将故障树(FTA)与层次分析法(AHP)结合使用来解决此问题，从定性转化为定量来进行多目标决策评价，该方法综合考虑权重的影响，能够快速对模糊问题进行客观评价。其基本步骤如下。

2.1 层次结构模型建立

由于故障树中的层次级数较多，并且不同故障模式下有可能对应相同的故障原因，因此层次结构较为复杂，不宜展开层次分析，为此结合可靠性分析方法，适当对故障树化简成能够使用层次分析，这里将Mi求得的最小割集作为相对应的最底层故障因素。采用Fussell下行法求得每一级的最小割集分别为：

M1最小割集为：{X1}，{X2}，{X7}；

M2最小割集为：{X2}，{X3}，{X7}；

M3最小割集为：{X4}，{X5}，{X8}，{X9}，{X10}，{X11}，{X12}，{X13}，{X14}；

M4最小割集为：{X2}，{X6}，{X11}，{X15}，{X16}，{X17}，{X18}；

综上所述，建立了电主轴系统失效的故障递阶模型，如图2所示。

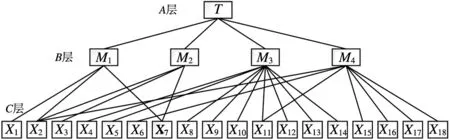
图2 电主轴失效的层次模型

2.2 故障原因发生概率权值求取

2.2.1构建判断矩阵

建立故障递阶模型后，通过分析每一层次的诸多因素相对于上一层次中的某一因素的相对重要性，对因素之间进行两两比较来构造判断矩阵以求得权重值，为了能够合理量化各因素的重要程度，因此引入萨迪标度作为比较的标度值[12]，如表3所示。

表3 萨迪相对重要度

经过深入机床企业调查，分析机床用户维修记录数据可以得到电主轴的失效模式和失效原因，再根据技术人员对故障因素的综合判断，便建立电主轴失效的故障模式概率权重的判断矩阵。采用MATLAB软件编写M1～M4因素相对于顶层T的判断矩阵程序，便计算出W=(ω1，ω2，ω3，ω4)的权重值，如表4所示。

表4 B层相对于A层判断矩阵B

表5是C层的故障因素发生概率判断矩阵C4。同理可求得M1，M2，M3的影响因素的权重判断矩阵C1，C2，C3(由于篇幅限制，此处不在累赘)。

表5 C层相对于B层判断矩阵C4

2.2.2 层次单排序一致性检验

层次单排序指的是同一层次的诸多因素相对于上一层次中某一因素的重要性排序。通常在构造因素判断矩阵时，虽然能够实现避免其它因素的干扰和客观反映一对因子影响力的差异，但是在多个因素的比较结果时，往往会出现非一致性现象，因此进行一致性检验是有必要的，其一致性计算公式如式(1)～ 式(3)所示。

(1)

(2)

(3)

式中，A为判断矩阵；n为判断矩阵的阶数；λmax为判断矩阵的最大特征值；R.I.为正反矩阵1000次的平均随机一致性指标，如表6所示。

表6 平均一致性指标R.I.取值

通常情况下，只要当C.R.<0.1或λmax=n，C.I.=0时，就表明该判断矩阵满足一致性要求，反之，则必须重新对该判断矩阵进行重新调整或修正，直至一致性指标满足要求为止。各判断矩阵一致性检验计算结果如表7所示。

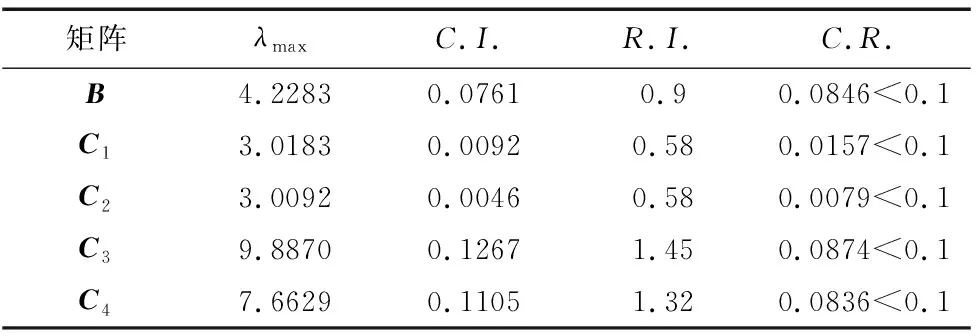
表7 最大特征根及一致性检验结果

通过一致性检验结果表明：各判断矩阵的C.R.i(i=1，2，3，4)值均小于0.1，这就说明在进行因素两两比较时的取值是合理的。

2.2.3 故障因素层次总排序

通过构造最底层的判断矩阵C1，C2，C3，C4，分别得到各故障因素的权重值，但是在整个系统可靠性分析中，故障因素单排序是不能够完全体现出相对于最顶层的故障权重排序，因此需要进一步对递阶层次模型进行故障因素层次总排序，逐层次计算出最底层故障因素相对于顶层事件的重要度权值总排序，方能进入下一步可靠性分析。各底层因素的总排序权重计算公式如式(4)所示。

(4)

各因素的权重计算结果如表8所示。

表8 各因素概率权重总排序

2.2.4 层次总排序一致性检验

虽然上述单层次排序满足一致性要求，但是在层次总排序一致性检验时，各层次的非一致性有可能累积起来，从而导致最终分析结果不能满足一致性要求，因此必须对层次总排序进行一致性检验[13]。检验表达式如公式(5)所示：

(5)

式中，C.I.j为Cj的一致性指标；

R.I.j为与Cj的平均随机一致性指标；

由公式(4)计算得：

C.R.=0.0338<0.1

计算结果显示：各权重的层次总排序是合理的、有效的，根据层次总排序结果可得到哪些故障因素对主轴系统造成影响较大，有针对性提出合理的可靠性改善措施来提高主轴系统可靠性。

3 关键故障因素可靠性改善措施

可靠性改善措施是兼顾经济与性能两方面，针对机床本身不足处加以纠正，目前国内的数控机床可靠性低，因此提出以下几点措施：

(1)装配完整机后，通过以往故障数据计算出早期故障时间拐点t1，作为整机在出厂前进行早期故障实验时间的一个参考依据，充分暴露出机床潜在故障，然后交与用户手上。

(2)对于外购件采购应该形成一套体系化的采购标准，对外购件质量严格把关。

(3)可靠性管理的系统化手段。在产品的设计、工艺、装配、质检等环节建立可靠性保证措施。

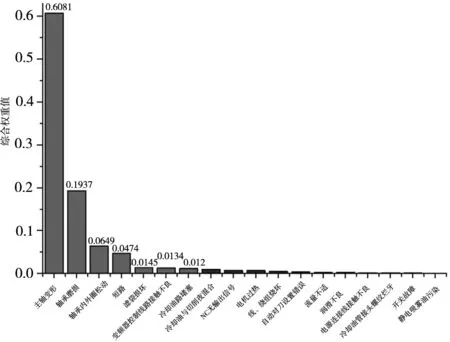
图3 故障因素综合权重排序柱状图

如图3所示，前7位故障因素对电主轴影响比较大，这7个底事件对应的单元为设计中的薄弱环节，因此将其作为影响主轴系统的关键故障因素，为了提高电主轴可靠性，这里有针对性的提出可靠性改善措施来降低关键故障因素的发生率，详细的可靠性改善措施见表9。

表9 关键故障因素可靠性改善措施

续表

4 总结

本文通过对主轴系统的FTA分析得到影响主轴系统失效的故障因素，考虑了各故障因素综合影响的基础上，结合层次分析方法(AHP)确定了造成主轴系统失效的前7位关键故障因素，最后提出可靠性改善措施来降低关键故障因素的故障发生率。在实际应用中，通过计算得到各故障因素的概率权值大小，可以在今后的检修中制定合理的诊断流程，克服在故障树中的徒劳故障搜索，很大程度上提高了故障诊断效率，大大缩短故障诊断时间，最终对提升主轴系统及整机的可靠性有着重要作用。