基于弹道逃逸和小推力捕获的地月转移轨道设计

彭坤，黄震，杨宏，张柏楠

中国空间技术研究院 载人航天总体部，北京 100094

随着美俄联合开展“深空之门”地月空间设施方案设计，开发地月空间已成为世界各航天机构的共识，同时往返地月空间也有助于获取月球以远载人深空探测所需的技术和经验[1-2]。而地月轨道转移方式及其转移轨道设计是开发地月空间的基础。目前已实施的月球探测工程主要有两种地月轨道转移方式：双脉冲地月轨道转移和全小推力地月轨道转移。美国的阿波罗载人登月工程[3]和中国的嫦娥月球探测工程[4]都采用了前者，即在近地轨道施加脉冲进入地月转移轨道以实现弹道逃逸，在近月点施加脉冲进入环月轨道以实现弹道捕获。其优点是轨道转移时间短，仅为3～5天，但由于采用化学推进方式，比冲低，推进剂消耗大。欧空局的SMAT-1卫星则采用全小推力变轨方式实施地球逃逸和月球捕获[5]。其优点是小推力发动机比冲高，节省推进剂，但由于推力小，飞行时间长约两百天，同时在地球逃逸过程中需要反复穿越范艾伦辐射带(高度范围为内带1 500～5 000 km，外带13 000～20 000 km)，对航天器的电子设备是严峻考验。为此，本文提出一种弹道逃逸和小推力捕获相结合的地月轨道转移方式，先利用运载火箭在近地轨道上脉冲加速将航天器送入地月转移轨道；进入地月空间后航天器利用自身的高比冲小推力发动机择机开机进行月球捕获，以取代近月点的脉冲制动，从而减少航天器燃料消耗。

基于弹道逃逸和小推力捕获的地月转移轨道设计主要涉及脉冲地月转移轨道设计、小推力地月转移轨道设计以及两段轨道拼接点选取等问题。脉冲地月转移轨道不同于单中心引力体脉冲变轨轨道，其非线性强，一般先在低保真模型中计算初值，再在高保真模型中修正初值以得到精确值。目前常用的低保真动力学模型有双二体模型[6]、三体模型[7,8]，以及伪状态模型[9,10]。也有学者直接在高保真模型中采用分层搜索流程[11,12]或基于高精度初值估计及改进修正方法[13]直接求解脉冲地月转移轨道。小推力转移轨道设计方法分为三类：间接法、直接法和混合法。Ranieri和Ocampo[14]基于间接法思想，用曲线拟合技术估计地球逃逸段和月球捕获段的伴随变量初值，并将月心伴随变量转换到地心系进行求解。Lee和Bang[15]则基于间接法理论采用最优螺旋曲线初值估计方法进行伴随变量初值估计并通过多层搜索逐步确定地月转移轨道。Betts和Erb[5]采用直接法将地月转移轨道离散化，再利用序列二次规划算法进行求解。由于地月小推力转移轨道飞行时间长，为保证轨道精度，离散化的状态变量和控制变量多达20万个，对于一般计算机而言属于海量计算。Pierson和Kluever[16]、Gao[17]等采用混合法思想，将地心段和月心段的伴随变量初值作为优化变量，采用非线性规划算法进行优化求解。徐明和徐世杰[18]则基于地月系统L1点Halo轨道构造了小推力地月转移自由飞行段，并设计合适控制律完成地球加速段和月球减速段轨道设计。对于基于弹道逃逸和小推力捕获的地月转移轨道，逃逸段和捕获段轨道的拼接也是其设计难点，若小推力发动机开机过早会过多消耗推进剂；若小推力发动机开机过晚则有可能不足以抵消脉冲地月转移轨道的对月速度，从而导致航天器月球捕获失败而逃离月球。目前还未有针对基于弹道逃逸和小推力捕获的地月转移轨道的综合设计方法研究。

考虑地月转移轨道主要受地球和月球引力影响[19]，本文在三体模型下建立地月转移轨道的动力学模型。对于弹道逃逸段，建立二维地心旋转系模型，采用地心旋转系对准角和地月转移加速速度增量作为控制变量，给出其初值估计的解析式，应用序列二次规划算法求解出满足目标约束的脉冲地月转移轨道。对于小推力捕获段，建立二维月心旋转系模型，进行逆向轨道仿真以提高轨道设计收敛性；以近月点伴随变量为优化变量，以月心距为基准进行逃逸段和捕获段轨道拼接以及目标约束设置；采用能量匹配观点预估转移时间，同时应用最优螺旋曲线伴随变量解析式预估初值范围；最后利用引导型人工免疫算法(Guiding Artificial Immune Algorithm，GAIA)对小推力月球捕获轨道进行优化求解，从而得到整条基于弹道逃逸和小推力捕获的地月转移轨道。

1 系统模型

基于弹道逃逸和小推力捕获的地月转移轨道飞行过程为：航天器在近地圆轨道(Low Earth Oribt，LEO)上运行，在A点施加切向脉冲Δv1，进入脉冲逃逸地月转移轨道(Ballistic Escape Trajectory, BET)，并在BET上无动力飞行；设到达B点时航天器小推力发动机开机进行减速制动，进入小推力月球捕获轨道(Low-Thrust Capture Trajectory, LTCT)，直至航天器到达近月点C进入目标环月轨道(CircumLunar Orbit，CLO)，其飞行轨迹示意图如图1所示。

忽略影响较小的摄动力，在圆型限制性三体模型下建立地心惯性系下航天器的动力学方程，如式(1)所示。其中月球绕地球以ω做匀速圆周运动，航天器只受到地球和月球引力作用。

(1)

式中：μE和μM分别为地球和月球的引力常数；Re为航天器相对地心的位置矢量，其标量长度为Re；Rm为航天器相对月心的位置矢量，其标量长度为Rm；RME为月球相对地心的位置矢量，其标量长度为RME。

设航天器在A点出发时刻为t0=0，以t0时刻地月连线为X轴，由地心指向月心，Z轴为月球轨道角动量方向，建立地心旋转系。将式(1)从地心惯性系转换到地心旋转系中，并进行极坐标变换x=rcosθ，y=rsinθ可得

图1 基于弹道逃逸和小推力捕获的 地月转移轨道轨迹Fig.1 Trans-lunar trajectory based on ballistic escape and low-thrust capture

(2)

对于小推力月球捕获轨道段，可建立月心旋转系下航天器极坐标运动方程，并加入小推力发动机摄动加速度，如式(3)所示。此时，地球作为次天体，其月心旋转系坐标为(-d,0)。

(3)

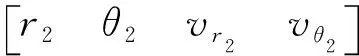
图2 二维地月极坐标系统Fig.2 Two-dimensional Earth-Moon polar coordinate system

2 弹道逃逸地月转移轨道设计

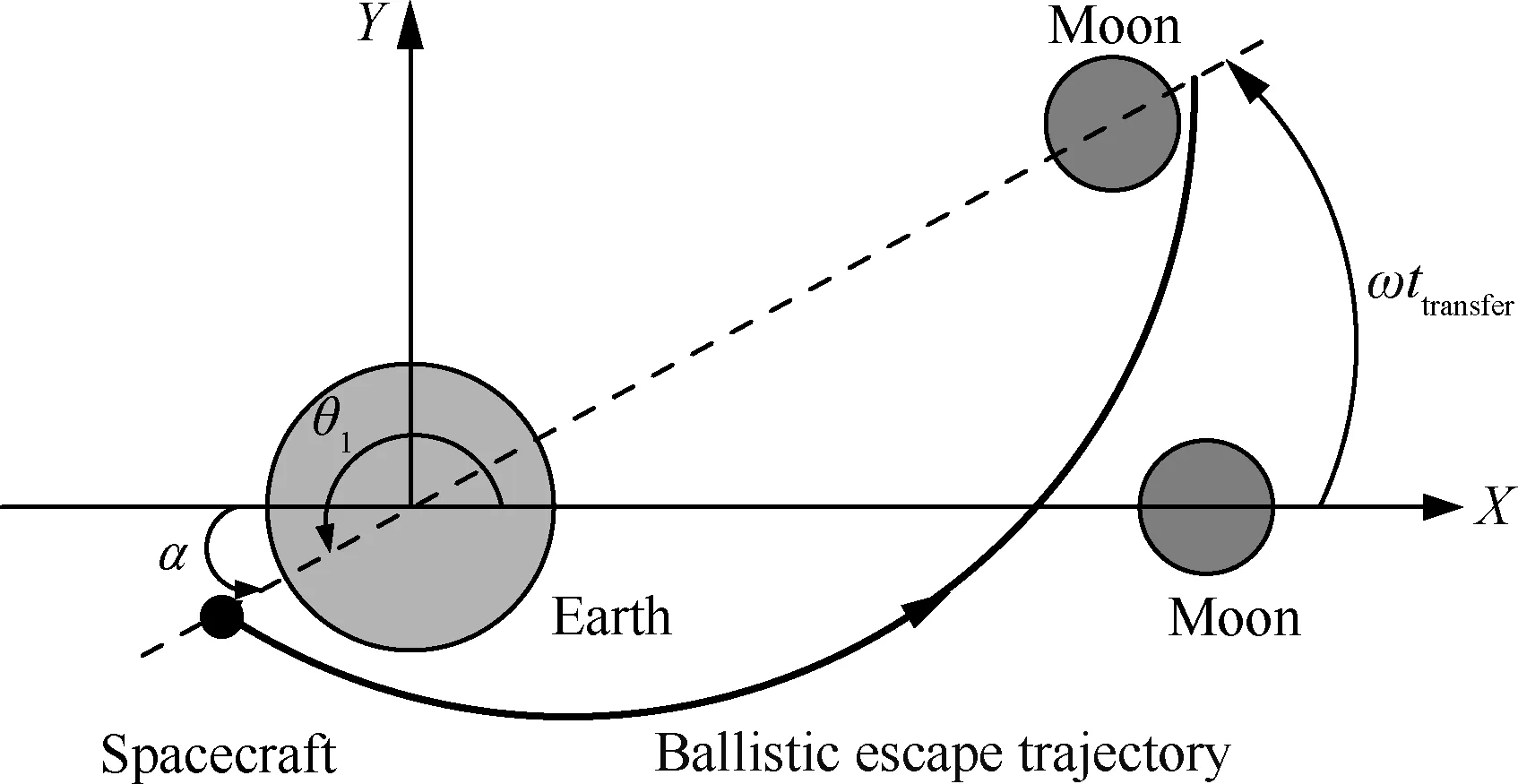
图3 地心旋转系下弹道逃逸轨道与 地月的几何关系Fig.3 Geometrical relationship between BET, Earth and Moon in geocentric rotating frame

(4)

为减少搜索过程中的轨道仿真时间，设置月心旋转系航迹角γ2的余弦值Γγ2满足式(5)的时刻tf为轨道积分终止条件，以保证航天器终端时刻处于近月点。

(5)

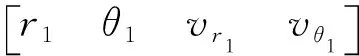
(6)

为满足近月距和转移时间约束，设置目标约束条件为

(7)

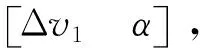
为增加轨道搜索的收敛性，需提供精确的设计变量初值。双脉冲地月转移轨道大部分轨道段主要受地球引力影响，本文将其近似为二体模型下的霍曼转移轨道，此时月球可看作一个普通航天器，忽略其引力影响。通过霍曼转移公式可给出计算Δv1的解析式；同时由霍曼转移轨道拱线应对准目标航天器交会位置可知，α等于转移时间ttransfer内月球公转转过的角度(如图3所示)。根据以上分析可给出设计变量初值估计解析式：

(8)

根据设计变量的初值估计值，本文采用常用的序列二次规划算法SNOPT[20]进行迭代求解。以下给出he=200 km，hm=2 500 km，ttransfer=5 d的地心顺行月心逆行的弹道逃逸地月转移轨道设计结果，如表1和图4所示。从表1可看出，对于5天地月转移轨道，初值估计值非常接近精确值；同时本文设计方法搜索速度快，迭代时间不到4 s，迭代4次就收敛到精确地月转移轨道。图4给出了地心旋转系下弹道逃逸地月转移轨道的轨迹。从图4可看出，该轨道大部分轨道段位于月球影响球外，主要受地球引力影响，验证了设计变量初值估计二体模型假设的合理性。

表1 弹道逃逸地月转移轨道搜索结果

图4 地心旋转系下弹道逃逸地月转移 轨道轨迹Fig.4 Ballistic escape trans-lunar trajectory in geocentric rotating frame

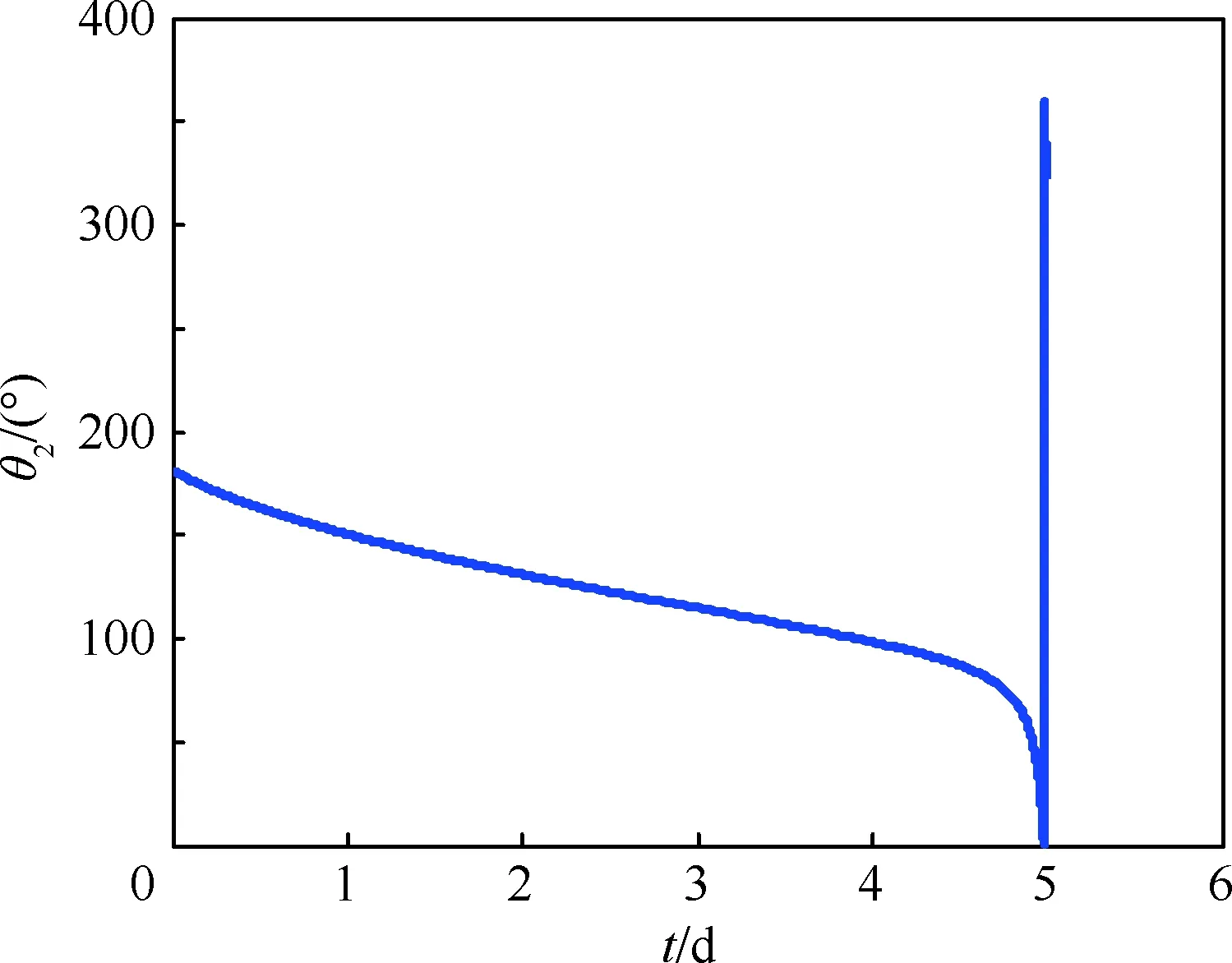
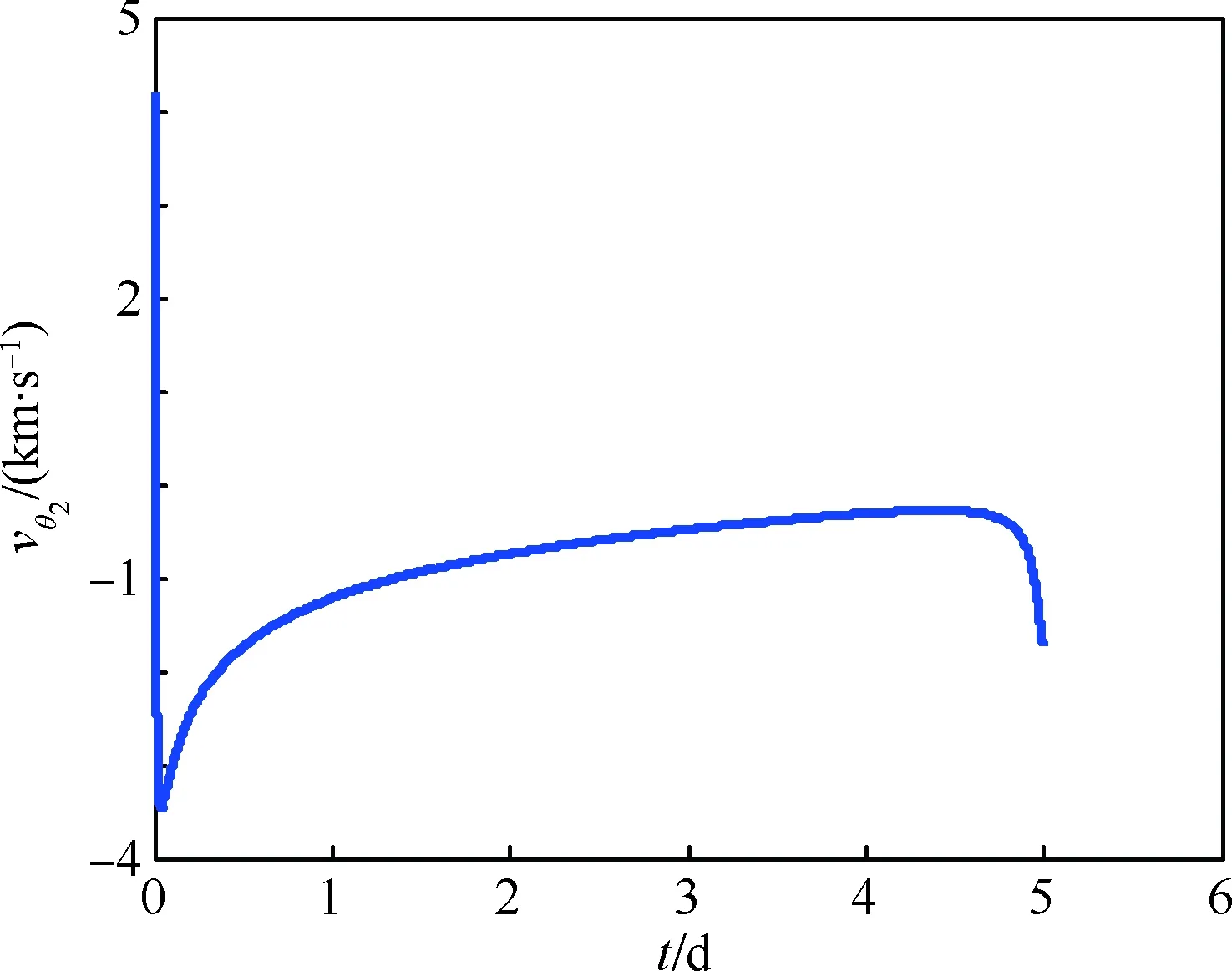
图5 月心旋转系下弹道逃逸地月转移轨道状态变量Fig.5 State variables of ballistic escape trans-lunar trajectory in selenocentric rotating frame

3 小推力月球捕获轨道设计

不同于脉冲转移轨道，小推力转移轨道是一条渐变螺旋轨道，需要设计转移过程中每一时刻的推力矢量。对于小推力月球捕获这类多圈轨道，转移时间长且月心距变化范围大。若采用间接法，由于多圈轨道的传递性，进一步增大了伴随变量初值的敏感性，初值猜测困难[17]。若采用直接法将轨道进行离散，为保证轨道设计精度，涉及海量设计变量搜索，计算过程复杂[5]。因此，本文基于混合法思想，采用GAIA[21]对伴随变量进行搜索求解。同时，小推力月球捕获轨道起始点B处于地月之间引力敏感区域(如图1所示)，动力学非线性强，而终端点C处于月球引力场中，轨道特性稳定。若直接从B点轨道顺推设计小推力轨道，初值敏感性进一步加强。为增加轨道搜索的收敛性，本文采用轨道逆推的方法设计小推力月球捕获轨道，以终端点C为轨道仿真起始点，而将起始点B作为轨道仿真终端点。

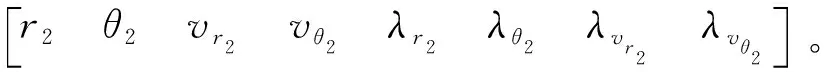
(9)

根据极大值原理，小推力最优控制角为

(10)

设C点时刻为tC=0，考虑目标环月轨道为逆行轨道，则轨道逆推的小推力月球捕获轨道初始条件为

(11)

式中：由于近月点C的极角θ2(0)自由，相应的伴随变量λθ2(0)=0。

(12)

一般拼接点的月心距较大，较小的θ2误差可导致较大的位置误差，因此θ2误差无法真实表征位置误差。这里将θ2约束转换为相对距离误差，则终端约束可进一步变为

(13)

小推力月球捕获轨道要求燃料消耗最小，同时考虑终端约束，将其作为罚函数引入评价函数。由于GAIA搜索极大值，故将评价函数设为如下形式，作为GAIA的亲和度值[21]。

{r2(-tLT)·

σ2|vr2(-tLT)-fvr2(r2(-tLT))|-

σ3|vθ2(-tLT)-fvθ2(r2(-tLT))|

(14)

式中：σ1、σ2和σ3为罚函数系数，采用模拟退火算法自动调整系数取值，σi=max{1,10/β(k/kmax-1)},i=1,2,3；k和kmax分别为当前寻优代数和最大寻优代数。

(15)

根据文献[15]的研究结论，τ可设为-0.012，κ为伴随变量等比例缩放系数。本文中κ的取值原则是保证3个伴随变量初值均大于1，使得3个伴随变量初值的搜索间隔足够大，从而使GAIA能进行充分的全局搜索。对于小推力捕获轨道的近月点C无角度要求，故θ2(0)∈[0°,360°]。

图6 弹道逃逸地月转移轨道月心能量Fig.6 Energy of ballistic escape trans-lunar trajectory in selenocentric frame

模型下小推力捕获轨道的能量和极径变化曲线，直至与弹道逃逸轨道的能量和极径完全匹配，此时的转移时间tLTguess可作为初值。

4 仿真算例及分析

设LEO为he=200 km的顺行轨道，CLO为hm=2 500 km的逆行轨道。设航天器到达近月点质量为m(0)=1 000 kg。考虑发动机推质比为4×10-3m/s2[15]，小推力发动机参数设为T=4 N。参考文献[17]，比冲取为w=3 500×9.8 m/s。弹道逃逸轨道选择ttransfer=5 d的脉冲地月转移轨道，其搜索结果见表1和图4。

取κ=50 000，根据初值估计公式可计算出λr2guess=12.55 723，λvr2guess=600，λvθ2guess=50 000。考虑一定搜索区域和各伴随变量的敏感性，设置伴随变量初值的搜索范围为λr2(0)∈[0.6λr2guess,1.4λr2guess]，λvr2(0)∈[-10λvr2guess,10λvr2guess]，λvθ2(0)=[1.2λvθ2guess,0.8λvθ2guess]。采用切向推力模式计算出脉冲逃逸轨道和小推力捕获轨道的能量-月心距曲线及其匹配点，如图7所示。匹配结果为tLTguess=4.425 d，此时r2=121 832.801 km，ε2=0.277 km2/s2。设左右偏差1.5 d，则小推力捕获轨道转移时间搜索范围为tLT∈[3,6] d。近月点C处极角搜索范围为θ2(0)∈[0°,360°] 。

根据以上搜索范围采用GAIA进行寻优搜索，种群个数为N=100，最大寻优代数为kmax=60，搜索到的弹道逃逸和小推力捕获的地月转移轨道结果如表2和图8～图10所示。由表2可知，小推力捕获轨道终端位置速度误差非常小，满足与弹道逃逸轨道的拼接点终端约束。小推力捕获轨道燃料消耗为39.670 kg，转移时间为3.940 d。

由图8可知，根据初值预估的搜索范围，GAIA在第10代就收敛到最优值附近，搜索速度快。图9绘制了小推力捕获轨道的轨迹，由图可知航天器经过约4圈轨道进入环月轨道。图10给出了小推力发动机的控制角变化曲线，由图可知越靠近月球，控制角振荡幅值越小，近似于切向制动。

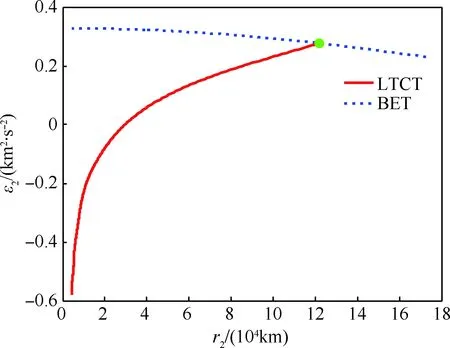
图7 弹道逃逸轨道和小推力捕获轨道的月心能量Fig.7 Energies of ballistic escape trajectory and low- thrust capture trajectory in selenocentric frame

表2 小推力月球捕获轨道搜索结果Table 2 Search results of low-thrust capture trajectory

图8 最大亲和度随迭代代数变化曲线Fig.8 Maximum affinity value of every generation

图9 月心旋转系下小推力捕获轨道轨迹Fig.9 Low-thrust capture trajectory in selenocentric rotating frame

图10 小推力捕获轨道的控制角Fig.10 Steering angle of low-thrust capture trajectory

图11绘制了整条弹道逃逸和小推力捕获地月转移轨道在地心旋转系和地心惯性系下的轨迹，其中虚线轨迹为不进行小推力捕获而沿着原脉冲逃逸轨道自由飞行的虚拟弹道捕获轨道(Virtual Ballistic Capture Trajectory，VBCT)。航天器在弹道逃逸轨道上飞行3.617 d后，小推力发动机开机进入小推力捕获轨道；在小推力捕获轨道上飞行3.940 d后到达目标环月轨道。其中，航天器在弹道逃逸轨道上飞行约1.2 h后地心高度超过20 000 km，即穿过范艾伦辐射带。

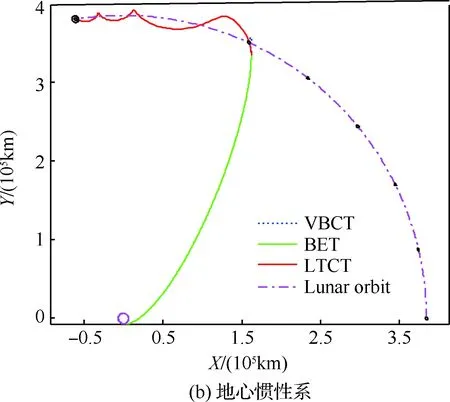
图11 基于弹道逃逸和小推力捕获的 整条地月转移轨道Fig.11 Whole trans-lunar trajectory based on ballistic escape and low-thrust capture

图12给出了整条地月转移轨道月心旋转系下的状态变量变化曲线，并与虚拟弹道捕获轨道进行对比。其中，两者的终端月心距和月心径向速度相同，而极角和月心横向速度不同。两者月心距相同说明均满足目标环月轨道高度约束，月心径向速度相同且为0说明了终端点均为近月点。极角不同说明两者的目标环月轨道入轨点不同，月心横向速度不同是因为虚拟弹道捕获轨道还未实施制动机动。若采用脉冲制动，需要速度增量647.507 m/s，设化学推进发动机比冲为310×9.8 m/s，则燃料消耗为199.568 kg，是小推力捕获轨道燃料消耗的5倍，说明了采用小推力捕获可大大节省燃料消耗。同时，采用小推力捕获方式总飞行时间为7.557 d，仅比5 d双脉冲地月转移轨道多2.557 d。因此，相对于全小推力地月转移轨道200 d左右的转移时间，以及双脉冲地月转移轨道3～5 d的转移时间，基于弹道逃逸和小推力捕获的地月转移轨道的转移时间适中。

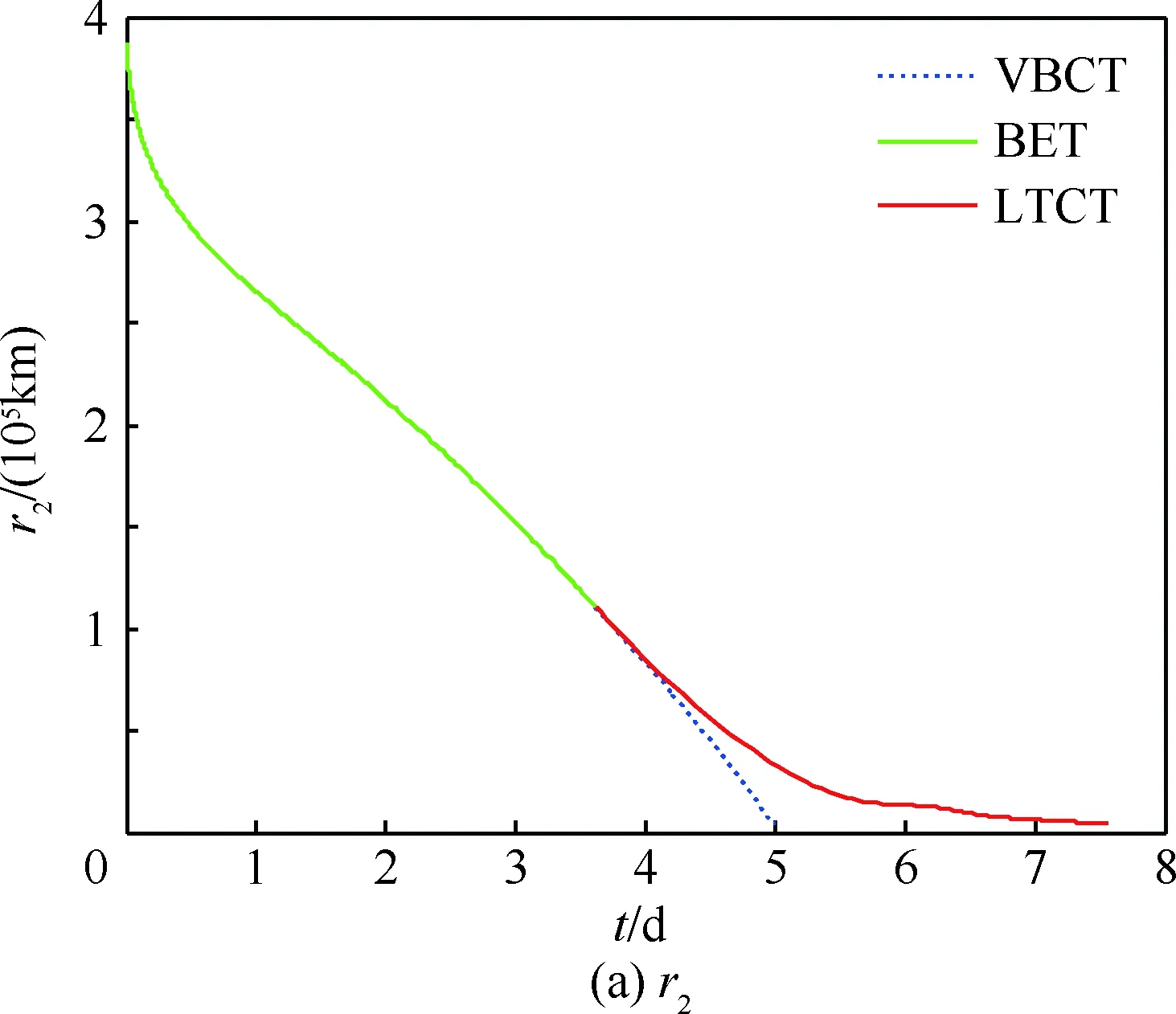
图12 月心旋转系下整条地月转移轨道状态变量Fig.12 State variables of whole trans-lunar trajectory in selenocentric rotating frame

5 结 论

1)对于运载火箭发射进入地月转移轨道的电推进月球探测器以及月球轨道空间站任务，提出了一种基于弹道逃逸和小推力捕获的新型地月轨道转移方式，并建立了二维极坐标系统模型。

2)将对准角和速度增量作为弹道逃逸轨道的设计变量，提出了初值预估解析式，仿真结果表明初值估计接近真实值，求解模型易于收敛。

3)利用月心距解决了小推力捕获轨道和弹道逃逸轨道的拼接问题。采用能量匹配和最优螺旋轨道伴随变量关系猜测初值范围，并以轨道逆推方式提高收敛性，实现了最优小推力捕获轨道的快速搜索。

4)与双脉冲地月转移轨道相比，基于弹道逃逸和小推力捕获的地月转移轨道近月制动燃料消耗约减少了80%，提高了航天器有效载荷比重或使航天器保留更多推进剂以延长其环月飞行寿命，同时其飞行时间仅增加几天时间。

5)与全小推力地月转移轨道相比，基于弹道逃逸和小推力捕获的地月转移轨道飞行时间降低了一个数量级，同时其利用弹道逃逸轨道不到2小时即可快速穿越地球辐射带。