基于一阶PPF的垂尾振动分数阶控制

牛文超，李斌，高振宇，王巍

西北工业大学 航空学院，西安 710072

现代高性能战机在进行高机动大迎角飞行时，飞机垂尾时常受到不稳定分离涡或者发动机等外激励的影响，垂尾结构会出现严重的振动疲劳问题。为此，从20世纪90年代，美国NASA等机构已对垂尾的振动抑制问题进行研究，文献[1]总结了20世纪90年代垂尾振动抑制的被动与主动控制形式，并指出基于压电材料抑制垂尾振动的发展方向。随后，Nitzsche等对比了加速度响应与动态应变响应作为反馈信号的垂尾抖振抑制性能，指出动态应变信号为反馈信号的性能更优[2]。Sheta等通过数值计算分析了采用压电片控制全尺寸F/A-18垂尾在最大抖振状态下的响应[3]，并采用2个单输入单输出控制器同时控制垂尾前2阶模态，但对一扭模态的控制效果不佳[4]。Browning等通过地面试验和飞行试验研究了F-16飞机腹鳍的压电抖振控制问题，验证了正位置反馈(PPF)和线性二次型高斯(LQG)控制对于抖振抑制的有效性[5]。针对不同飞行状态(迎角、风速)下控制系统的鲁棒性，Chen等分别采用H∞[6]和μ[7]综合控制对垂尾的抖振控制进行研究。国内，陈仁文等采用压电作动器设计了垂尾减振系统[8]，王巍等根据主模态控制思想设计了垂尾抖振主动控制系统[9]。冷劲松等验证了宏纤维压电复合材料(MFC)作动器对于垂尾抑制的有效性[10]，杨智春等采用压电载荷等效方法对MFC压电作动器建模，提出一种基于输出可控性的压电作动器优化准则，以提高压电作动器在垂尾抖振抑制的性能[11]。综合上述文献可以看出，对于构建的飞机垂尾振动主动控制系统：一是要具有良好的鲁棒性，能够适应附加气动阻尼或气动刚度效应带来的结构动力学特性的时变性；另一方面要求控制系统在传感和驱动方面简洁实用，易于实现。PPF控制器是一种典型的针对目标模态实施主动控制的方法[12]，结构简洁，易于实现，因此已广泛用于基于压电驱动的航空航天等柔性结构的振动抑制中[13-14]。PPF控制器的基本原理是在传感/驱动共位配置的基础上，在反馈回路中增加一个相位补偿环节，使得驱动器实时输出一个与原始振动反向的响应以抵消原结构的不利振动[13]。经典PPF控制器按补偿器微分方程的阶次可分为一阶PPF与二阶PPF形式。二阶PPF控制器对于目标模态频率过于敏感，当系统发生模态频率偏移时，易出现控制溢出问题。针对上述问题，Rew等基于频率在线估计方法，提出一种用于摄动系统的自适应PPF控制器，提高了PPF控制器的鲁棒性[15]，但在有些工况下频率在线估计的波动性和误差较大，严重影响了控制器的性能。Baz等结合独立模态空间方法，将PPF控制器简化为一阶补偿器的形式[16-18]，改善了控制器在高于目标模态频率频段内的相位补偿效果，使得控制器对高阶模态的振动响应具有良好的抑制性能[16]。不过经典的一阶PPF控制器依然对结构固有频率的变化较为敏感，尤其当结构的目标模态频率向低频方向摄动时，控制器鲁棒性较差。

高性能战机的垂尾发生抖振时，受附加气动刚度等因素的影响，其主振动成分的频率具有典型的时变特性，传统的振动主动控制器往往不能满足实际要求。新兴的分数阶控制器具有可调参数多、控制器设计灵活、鲁棒性强等特点[19]，可以改变传统整数阶控制器在整个目标频段内的频域特性，为问题的解决提供了新的方向。本文针对飞机垂尾振动主动控制的需要，基于分数阶微积分理论与一阶PPF控制器构造分数阶(FOPPF1) 控制器。该控制器相比二阶PPF控制器仅增加了一个设计参数，但控制器设计的灵活性明显提高。该控制器通过调节一阶PPF控制器的频域特性，改善控制器对于摄动系统的振动抑制性能。综合考虑随机响应的频域特性与整体波动强弱，给出了该控制器参数的优化调节方法。并以一个粘有MFC压电片的垂尾试验模型为例，利用粒子群算法设计出相应的FOPPF1控制器，并通过仿真与试验分析验证该控制器的优异性能。

1 一阶PPF控制器

传统一阶PPF控制系统的原理框图如图1所示，其中G1(s)为外激励Fp与传感器响应d的传递函数，G2(s)为控制电压u与传感器响应y的传递函数，在反馈回路中添加一个一阶补偿器K(s)，即一阶PPF控制器的传递函数，y为作动器引起的振动响应信号，与结构无控时的响应d叠加相消后达到振动抑制的效果，e为结构参考点测得的残差振动响应。一阶PPF控制器与PPF控制器的原理基本相同，通过引入一个高阻尼的补偿器提高控制系统的阻尼，达到振动抑制的目的。

根据文献[20]，对于任意一个多自由度系统，设被控目标模态的运动方程与对应的一阶PPF控制器分别为

(1)

(2)

(3)

为保证控制器对结构目标模态具有良好的控制效果，需令ωf=ωc。

一阶PPF控制器的不足之处表现在：ωf一旦设定，当被控结构由于参数摄动，出现目标模态的响应频率偏移时，控制系统易不稳定，作动器输出的响应y与原结构开环响应d之间的相位差可能不在90°～270°之间，引起控制反效；若将ωf设为远小于结构的固有频率，虽然可以满足相位补偿的需要，但是控制器传递函数在目标频段的幅频特性又被破坏，导致控制输出过小，不能满足实际要求，且带来低频段的溢出问题。

图1 一阶PPF控制系统的结构框图Fig.1 Block diagram of the first-order PPF control system

2 基于一阶PPF的分数阶控制器

若能利用分数阶来改善传统一阶PPF控制器的幅频与相频特性，既保证控制器在目标频段内的相频曲线尽量水平，又能维持良好的幅值传递特性，则可以降低控制器对结构固有频率时变的敏感性，提高传统一阶PPF控制器的鲁棒性。

目前常见的分数阶微积分的定义形式有：Grünwald-Letnikov (GL)定义、Riemann-Liouville (RL)定义与Caputo定义。Caputo定义更适合分数阶微积分初值问题的求解，并且其Laplace变换形式更为简洁[21]，因此本文采用Caputo的定义形式。

基于一阶PPF构造FOPPF1控制器的基本思路为：在传统一阶PPF控制器微分方程的基础上，将整数阶微积分扩展为在一定范围内变化的分数阶微积分，新增2个可调参数Δ1和Δ2，提高一阶PPF控制器的设计空间，改善控制器性能。

FOPPF1控制器的动力学方程为

(4)

(5)

其中：t0和t为运算上下限；α为阶次；Re(α)为α的实部。则FOPPF1控制器的Laplace变换形式为

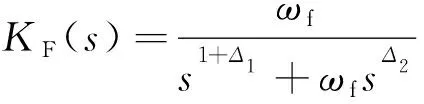
(6)

由式(6)可知，传统一阶PPF控制器只是FOPPF1控制器的一种特殊形式，FOPPF1控制器包含无数个设计点，而一阶PPF控制器只有一个设计点(1, 0)。

为使2个分数阶参数在仿真中相互独立，方便控制器设计，将式(6)变换为

(7)

令a=-Δ1,b=Δ2-Δ1，则式(7)可写为

(8)

根据经验，该传递函数化简后，各项幂指数的最大调节范围为[-0.6,0.6]。式(8)对应的FOPPF1控制器的仿真框图如图2所示。其中In(t)与Out(t)分别为控制器的输入与输出，ωf=ωc。

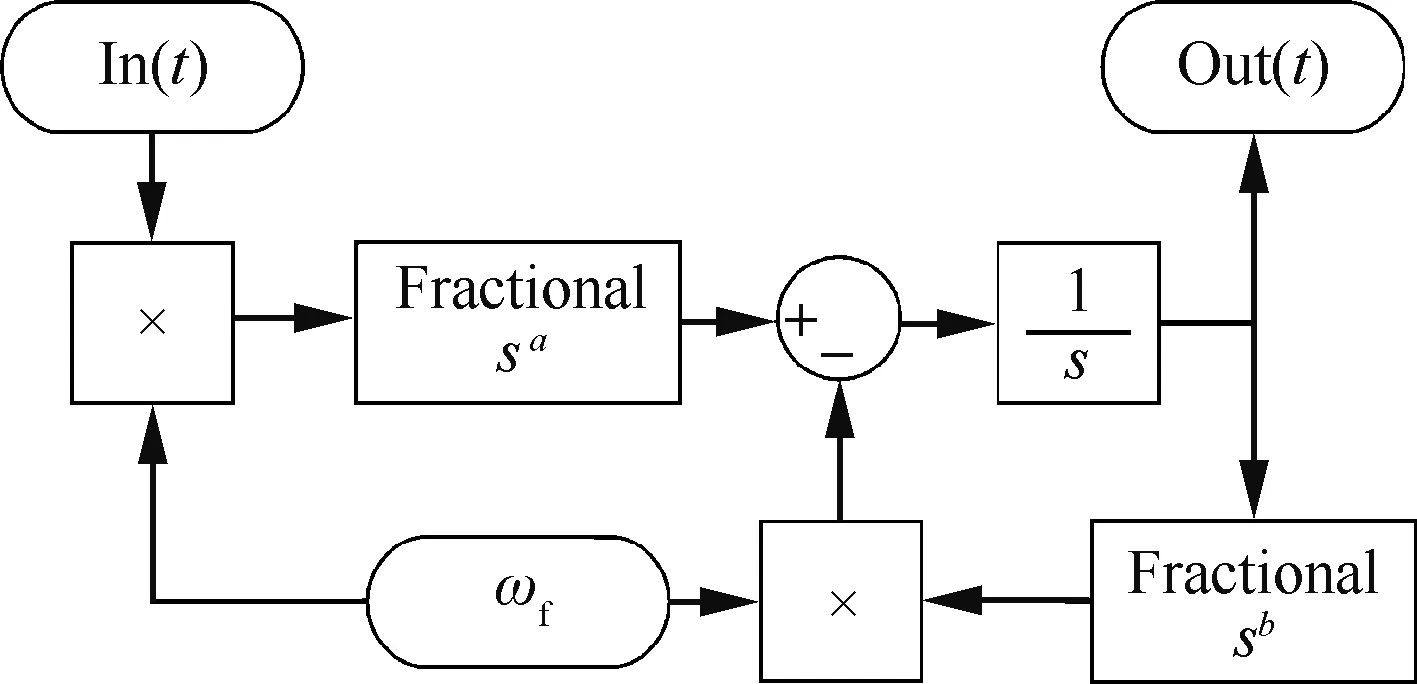
图2 FOPPF1控制器框图Fig.2 Block diagram of FOPPF1 controller

3 FOPPF1控制器的优化设计

考虑到垂尾结构振动一般具有窄带随机的特性，因此本文采用随机激励为设计输入。控制器的设计目标是寻找一组最优的控制器参数能够将被控结构的主振动成分及总体振动幅值抑制到最低水平。

对于任意一组给定的控制器参数，假设已获得系统精确的结构动力学标称模型。根据被控结构的实际工作情况，定义一段典型的时域随机激励作为系统的输入，采用如图3所示的MATLAB仿真框架，则可以计算得到开环系统与闭环系统的时域随机响应yo与yc，并同时计算yo与yc对应的功率谱密度(PSD)与均方根值(RMS)。

图3 MATLAB仿真框图Fig.3 Block diagram of MATLAB simulation

定义闭环系统随机响应PSD谱峰值的降低比为

(9)

式中：Po为开环系统随机响应PSD谱的峰值；Pc为闭环系统随机响应PSD谱的峰值。

定义闭环系统随机响应RMS值的降低比为

(10)

式中：Ro为开环系统随机响应的RMS值；Rc为闭环系统随机响应的RMS值。

设FOPPF1控制器的设计变量为x=(a,b)，控制器参数的优化目标为被控结构在给定激励作用下闭环系统的PSD谱峰值降低比和RMS值降低比的加权和最大，则目标函数h可定义为

(11)

相比其他传统优化算法，粒子群算法具有原理简单、收敛速度快等特点，已广泛用于分数阶控制器设计，并得到了理想的优化结果[16]，因此本文采用粒子群算法进行式(11)所描述的优化问题的求解。

4 垂尾模型的FOPPF1控制器设计

4.1 试验模型

本文以如图4所示的根部固支垂尾模型为对象进行研究，该垂尾为真实垂尾1∶2的缩比模型，其质量约为17.3 kg，具体尺寸如图4所示。被控目标模态选为垂尾一阶弯曲模态，其标称状态下的固有频率为13.5 Hz，模态阻尼比为0.012 2，激励力的涵盖频段为[5, 20] Hz。在垂尾根部的两侧面各对称贴6片MFC压电片，施加主动控制力，课题组前期采用拓扑优化选取MFC驱动效率最高的区域，并采用文献[11]中方法确定压电片的布局。MFC压电片通过高压功率放大器(HVA 1500/50-4, Smart Material Corp.)驱动。在地面振动控制试验中，采用电磁激振器(JZK-10, Sinocera)在垂尾根部施加激励以模拟垂尾受到的气动载荷。使用半实物实时仿真系统Quanser进行振动主动控制试验。以垂尾根部应变响应为反馈信号，应变信号通过动态应变仪(DH3840, 东华)进行采集，数据分析采用Vibrunner (m+p International)。

为了检验本文所设计的控制器对结构固有频率发生摄动时的适应性，本文设计了2种垂尾摄动试验模型的构建方案。在地面振动控制试验中，增加垂尾结构固有频率的试验系统往往过于复杂，为简化试验方案，本文均采用在垂尾端部附加质量的方式减小结构的固有频率，2种方案为：① 固定质量块方案，通过调整固定质量块的数量，阶梯式改变垂尾结构的质量，以模拟垂尾固有频率在飞行中的突然摄动问题；② 沙斗配置方案，在振动过程中实时往沙斗中增加铁砂实现垂尾模型质量的缓变调节，从而模拟垂尾固有频率在飞行中的缓变摄动问题。2种摄动试验模型的配置如图5所示。

图4 试验模型与试验系统Fig.4 Experimental model and system

图5 摄动模型构建方案Fig.5 Construction scheme of perturbation model

4.2 系统辨识与控制器参数设计

首先对处于标称状态的垂尾模型进行系统辨识，获得标称垂尾结构的动力学模型，用于控制器设计与仿真分析。辨识模型的输入为高压功率放大器的输入电压，设定为幅值2 V的2～22 Hz正弦扫频信号，扫频时间为30 s，采样频率为1 024 Hz。辨识模型的输出为垂尾根部应变响应。利用MATLAB系统辨识工具箱可辨识建立垂尾的标称动力学模型，并得到其传递函数，记为G0(s)。试验模型与辨识模型的Bode图如图6所示，二者频域特性基本贴合，辨识模型的精度可满足实际要求。

图6 试验模型与辨识模型的Bode图Fig.6 Bode diagrams of experiment model and identification model

通过激励源输入一个带宽为[5, 20] Hz的随机激励，激励信号PSD谱峰值为0.001，仿真时间为20 s，时间步长为0.001 s，分数阶微积分算子采用改进Oustaloup方法进行逼近计算。采用第3节的目标函数与仿真框图，通过粒子群算法进行优化，得到FOPPF1控制器的最优参数为：a=0.291 2，b=-0.524 9。

4.3 FOPPF1控制器的频域特性

为了分析4.2节基于垂尾标称状态所设计的FOPPF1控制器对摄动模型的适用性。本文通过辨识方法同理建立如图5所示的固定质量块摄动方案的动力学模型，其中单个质量块的质量为0.96 kg，共2个质量块，固有频率的摄动量为-22.2%。应用数值分析方法对比分析FOPPF1控制器与经典一阶PPF控制器对标称模型和摄动模型的控制性能差异。

图7给出了相同增益下2种控制器在目标频段的Bode图，从相频图中可以看出，在目标频段[5, 20] Hz内，FOPPF1与一阶PPF控制器的最大相角变化量分别为17.8°和35.6°，FOPPF1控制器相频曲线的变化量相比一阶PPF减小了50%，且在10～20 Hz频段的相角几乎保持恒定。相角变化小，意味着控制器在目标频段内可以提供相对稳定的相位补偿，只要被控结构固有频率的摄动量不超过其相位稳定补偿区，控制器将不会发生控制效率显著下降或控制溢出。从幅频图中可以看出，FOPPF1的幅值明显高于一阶PPF控制器，因此相同增益下，分数阶控制器的输出也会更大。以上分析表明，FOPPF1控制器的鲁棒性和控制效果相较一阶PPF均有显著增强。

为验证FOPPF1控制器对于摄动系统的鲁棒性，图8分析了FOPPF1与一阶PPF控制器在被控结构模型给予一定摄动时，闭环控制系统的极点分布变化，采用本节辨识的固有频率摄动量为-22.2%的摄动模型，控制器的增益与后文试验相同，分别为0.016和0.09。为了更清楚观察闭环系统的极点随摄动量的变化，图中没有画出那些远离虚轴的具有稳定特性的极点。从极点分布图中可以看出，当被控结构模型引入当前的固有频率摄动量后，FOPPF1控制系统靠近虚轴的极点位置基本不变且都继续位于虚轴的左半平面，因此控制系统继续维持稳定状态；而当被控结构模型引入相同的固有频率摄动量后，传统一阶PPF控制系统靠近虚轴的极点位置发生了显著改变，原本在标称状态下位于虚轴左半平面的极点移动到了虚轴的右半平面，说明摄动模型下一阶PPF控制系统已经发散。闭环系统的极点变化再一次表明，本文提出的FOPPF1控制器对于结构固有频率的摄动不敏感，其鲁棒性明显高于一阶PPF控制器。

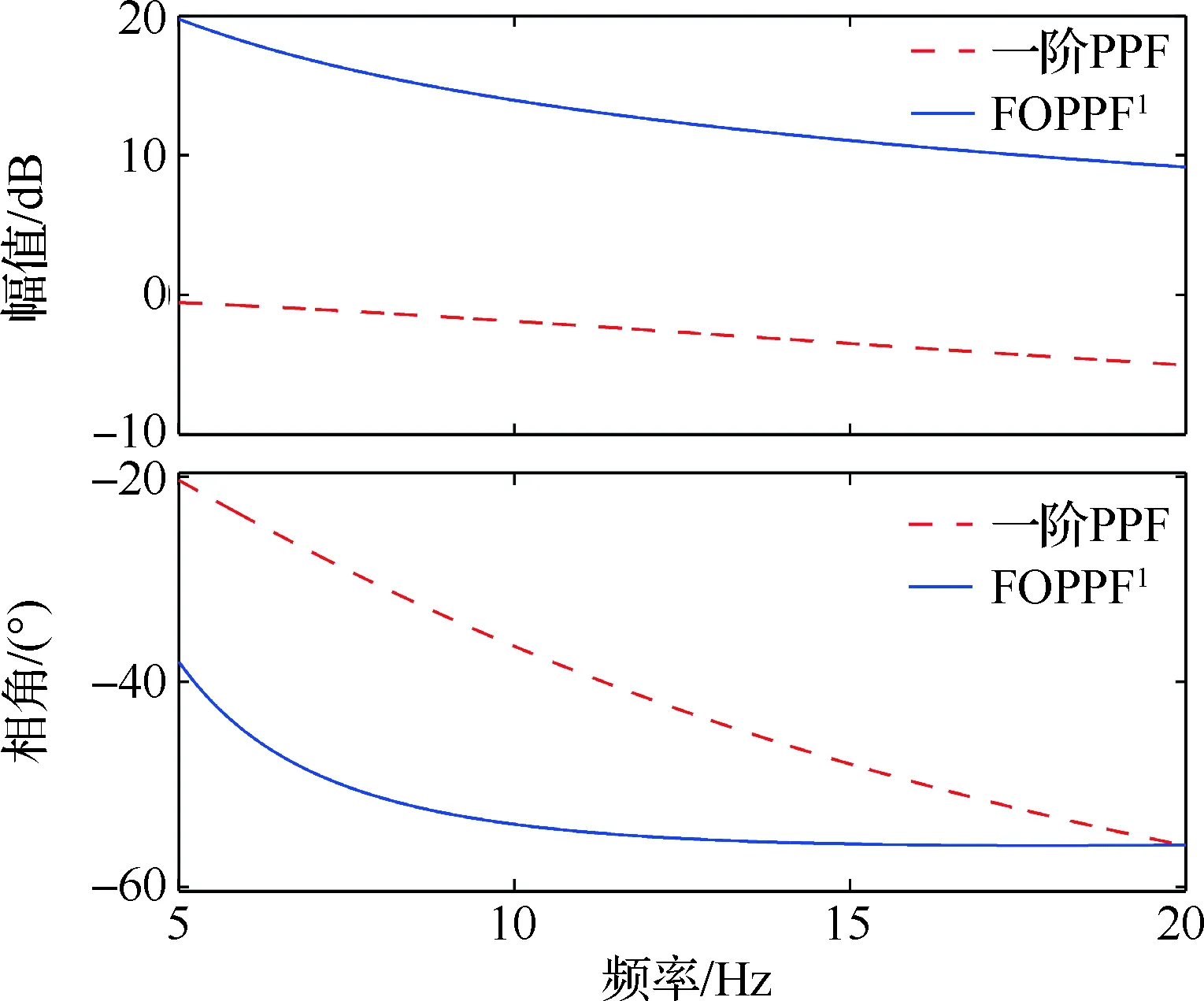
图7 2种控制器的Bode图Fig.7 Bode diagrams of two controllers

图8 控制系统的极点分布Fig.8 Pole distribution of control systems

5 试验验证与讨论

本节将通过垂尾的振动主动控制试验，验证FOPPF1控制器的有效性，并与一阶PPF控制器进行对比，控制器参数与4.2节相同，振动主动控制试验系统如图4所示。由于被控目标模态是垂尾一阶弯曲模态，因此在反馈回路增加了一个[5，20] Hz的4阶带通滤波器，滤除结构响应中的高阶成分。验证试验包括：自由振动响应控制试验和随机响应控制试验2种形式。

5.1 自由振动响应控制试验

自由振动响应控制试验的目的为观测主动控制器带来的等效阻尼效应。以处于标称状态的垂尾结构为试验对象，在垂尾根部施加与标称垂尾结构一阶弯曲固有频率13.5 Hz一致的定频正弦激励力，使得垂尾处于稳态振动状态。然后瞬间关闭激振器，并同时开启主动控制器，测得结构的自由振动响应，如图9所示，并采用对数减幅率方法计算结构的等效阻尼比，试验结果如表1所示。从图表中可以看出，FOPPF1控制器的衰减持续时间最短，该控制器可实现的等效阻尼比相比一阶PPF控制器增加了50.1%。

图9 自由振动响应Fig.9 Free vibration response

表1 结构阻尼率与稳定时间Table 1 Structural damping ratio and settling time

参数阻尼率稳定时间/s开环状态0.012 25.61FOPPF10.070 70.67一阶PPF0.047 11.08

5.2 随机响应控制试验

为了验证典型的窄带随机激励下，主动控制器对于标称模型与摄动模型的控制效果与鲁棒性，本节分别以处于标称状态与摄动状态的垂尾结构为试验对象，在垂尾根部施加频带为[5, 20] Hz的随机激励，测试2种控制器对于随机振动的抑制性能。

5.2.1 阶梯摄动结构的随机响应控制试验

试验对象为采用固定质量块调节方案的阶梯摄动试验模型，所加单个质量块的质量为0.4 kg，共增加2个质量块，垂尾模型摄动后的固有频率为12.0 Hz，固有频率的摄动量Δωc为-11.1%。所谓阶梯摄动方案为：开始试验前，质量块已经调整到位，属于一种离线摄动形式。为保护压电片和高压功率放大器的安全，文本选取外激励载荷的原则为：在试验过程中，MFC的最大输入电压小于200 V。若试验中压电片的最大输入电压小于限压保护器阀值，则控制器的控制效果基本不受外激励大小的影响。

图10给出了标称试验模型和阶梯摄动试验模型分别采取开环、一阶PPF和FOPPF1控制时，垂尾根部应变响应的PSD谱。表2给出了相应的PSD谱峰值降低量(与开环情况对比)和RMS值降幅比(与开环情况对比)及控制器输出电压的RMS值(表征控制能耗)。

图10 随机响应的PSD谱Fig.10 PSD spectra of random response

对标称垂尾模型(Δωc=0%)，由测试结果的对比分析可知，FOPPF1和一阶PPF控制器在结构共振峰区域均获得较好的控制效果，达到抑制主模态振动成分的目标，且相比而言，FOPPF1比一阶PPF的控制效果更优。对标称垂尾模型，施加主动控制后，结构响应的RMS值与无控状态相比均降低了约60%，两者控制效果相当，FOPPF1仅比一阶PPF多降低了1.5%。但FOPPF1控制系统可达到的PSD谱峰值衰减量较一阶PPF控制系统提高了3.8 dB。若用“结构响应RMS值每降低1%所需控制电压的RMS值”来度量控制能耗率，则可发现，FOPPF1控制系统响应的RMS值每降低1%所需电压的RMS值为0.824 V，而一阶PPF控制器为0.904 V，该FOPPF1控制器所需能量的能耗率比一阶PPF控制器低约9%。

对阶梯摄动垂尾模型(Δωc=-11.1%)，一阶PPF控制器的控制效果显著降低，RMS的降低比仅有25.5%，而FOPPF1控制系统翼根应变响应RMS值的降低比可达58.4%，与标称模型时的控制效果相当，且此时FOPPF1控制器获得的PSD谱峰值衰减量较一阶PPF控制器多了8.3 dB，控制能量的能耗率约只有一阶PPF控制器的28%。

为了进一步寻找FOPPF1控制器的稳定边界，本文还进一步增大附加质量快的质量，加大一阶弯曲固有频率的摄动量。试验结果表明，当垂尾模型的固有频率降低为11.5 Hz时(Δωc=-14.8%)时，FOPPF1控制器可获得的RMS值降低比仍为45.7%，而一阶PPF控制器已经发散。

以上试验结果表明，对于阶梯摄动模型，FOPPF1控制器不仅显著提高了其鲁棒性，且控制效果和能耗率也比一阶PPF控制器明显提高。

表2 随机响应试验结果Table 2 Experimental results of random response

5.2.2 在线摄动结构的随机响应控制试验

飞行器垂尾结构发生振动时，其固有频率摄动往往在一定范围内具有在线时变特性。为进一步说明FOPPF1控制器对于在线摄动结构的有效性，本节分别进行了垂尾固有频率在线缓变与在线突变2种试验。在线缓变试验过程中，通过在垂尾梢部的2个容器中增加铁砂来实时改变垂尾的固有频率，即沙斗配置方案，单个容器装满铁砂时的总质量为0.4 kg。在线突变试验过程中，通过突然在垂尾顶端在线吸附2个质量块引起垂尾固有频率突变，单个质量块的质量也为0.4 kg。因此最大摄动状态下固有频率的摄动量Δωc=-11.1%。

保持随机激励输入与5.2.1节相同，在2种在线摄动模型下，FOPPF1控制器在开环与闭环状态下测得的垂尾根部应变响应的PSD谱如图11所示。FOPPF1控制器对在线缓变摄动模型可获得的RMS值的降低比为53.5%，对在线突变摄动模型为59.4%，对应的PSD谱的峰值衰减量分别为10.38 dB与14.73 dB。试验结果表明，FOPPF1控制器具有良好鲁棒性，对结构固有频率的在线变化同样不敏感。

图11 在线摄动结构的随机响应PSD谱Fig.11 PSD spectra of random response of perturbation structure online

6 结 论

1) 基于分数阶微积分理论，在一阶PPF控制器的基础上，引入2个分数阶项，提出一种FOPPF1控制器。并构造了控制器参数优化设计的目标函数，采用粒子群优化算法可得到有效的控制器参数。

2) 相比一阶PPF控制器，FOPPF1控制器在目标频段内的相频曲线变化平缓，可实现有效的相位补偿，且闭环极点对参数摄动不敏感，使得控制器具有良好的鲁棒性。

3) 以一个一端固支且粘有MFC压电作动器的垂尾为例，设计了相应的FOPPF1控制器，通过振动主动控制试验验证了FOPPF1控制器的优异性能。试验结果表明，FOPPF1控制器的控制效果与鲁棒性均明显提高，不同摄动模型下随机响应的RMS值降低比达到58.4%，对参数在线摄动结构也有显著的控制效果，并且该控制器的能耗率低，具有良好的应用前景。