缝式机匣处理及其轴向偏转角对跨声速轴流压气机稳定性的改善

2018-08-29张皓光谭锋安康楚武利吴艳辉

航空学报 2018年8期

张皓光，谭锋，*，安康，楚武利，2，吴艳辉，2

1. 西北工业大学动力与能源学院，西安 710072 2. 先进航空发动机协同创新中心，北京 100083

压气机的稳定性是航空发动机必须面临的问题，当压气机运行在不稳定工况时(失速和喘振)，不仅会降低性能参数，而且会产生强烈振动，甚至会导致叶片断裂。因此，提高压气机的稳定裕度是设计高性能压气机的关键技术。现阶段，多数压气机的失速起始于叶顶，可以采用端壁处理技术提高压气机的稳定裕度。相比于叶顶喷气和端壁造型，机匣处理的扩稳能力更好。

机匣处理最早由Koch和Smith通过试验“意外地”发现[1]。早期机匣处理的结构类型有孔式和蜂窝式[2-4]，随着试验条件的成熟和计算机技术的发展，机匣处理已经演变出来多种结构类型，例如槽式[5-6]、缝式[5-6]以及自循环式[7-10]等。槽式机匣处理在降低1%左右压气机效率的基础上能够获得10%以下的稳定裕度改进量[5-6]。相比于槽式机匣处理，缝式机匣处理的扩稳效果显著，能够获得20%以上的稳定裕度改进量，但是压气机效率的损失较大[5-6]。与槽式和缝式机匣处理相比，自循环式机匣处理的扩稳能力较小，仅仅能够获得5%以下的稳定裕度改进量，但是可以提高1%左右的压气机效率[7-10]。

缝式机匣处理的扩稳效果显著，国内外学者投入大量的时间和精力来探索和澄清缝式机匣处理的结构类型和扩稳机理，主要集中在轴向缝、轴向倾斜缝以及叶片角向缝等方面，特别是轴向倾斜缝。Osborn[5]和Moore[6]等开展了缝式机匣处理的试验研究。结果表明，轴向缝在降低6%左右峰值效率的基础上获得15.8%的稳定裕度改进量，轴向倾斜缝在降低7%左右峰值效率的基础上获得20%的稳定裕度改进量，而叶片角向缝降低了近失速边界的总压比，其扩稳效果较差，但是基本不影响效率。Takata和Tsukuda[11]的试验研究表明，机匣处理扩稳效果的好坏与压气机效率的损失成反比，扩稳效果越好对应的效率损失越大，反之亦然。刘志伟等[12-13]的试验结果与Osborn[5]和Moore[6]等的存在差异。结果表明，轴向倾斜缝的扩稳效果最好、叶片角向缝次之、轴向缝最差。轴向倾斜缝前伸在保持扩稳效果基本不变的基础上能够显著降低效率损失，而轴向倾斜缝后移是以牺牲扩稳效果为代价减少效率损失。

Wilke和Kau[14-15]开展缝式机匣处理的数值模拟研究。结果表明，轴向倾斜缝前伸在进一步提高压气机稳定裕度的基础上降低了效率损失。轴向倾斜缝及其前伸通过减弱泄漏流的卷起和消除泄漏涡的破碎，降低泄漏涡涡核的总压损失，从而提高压气机的稳定裕度。周小勇[16]通过数值模拟开展轴向倾斜缝及其轴向叠合量的研究。不同轴向叠合量的轴向倾斜缝均提高了压气机的稳定裕度，但是均降低了压气机的峰值效率。80%轴向叠合量的轴向倾斜缝的扩稳效果最好，而50%轴向叠合量的轴向倾斜缝的效率损失最小。除了轴向位置，缝式机匣处理的缝长、缝深、缝宽以及缝数等对其扩稳效果和效率损失的影响同样不可忽视。马宁[17]以端区流动损失为目标函数，开展轴向倾斜缝结构参数优化的数值模拟研究。随着缝数的增加、缝深的降低以及缝宽的增大，压气机的设计点效率呈现下降的趋势，并且叶顶损失系数越大，设计点效率降低得越多。随着缝数的增加和缝宽的增大，缝内回流的流量提高，叶顶上游损失增加、下游损失减少，而随着缝深的降低，缝内回流的流量降低，射流速度的方向靠近叶顶通道上游，叶顶损失沿着轴向升高。

截至目前，缝式机匣处理的走向大致可以分为平行压气机旋转轴的方向和沿着叶片安装角的方向这两种。试想如果将缝式机匣处理的走向沿着叶片安装角的相反方向安置，其对压气机稳定性的影响会是怎样的，不同轴向偏转角的缝之间的扩稳能力和扩稳机理有什么区别。鉴于此，本文以NASA Rotor 67为研究对象，采用非定常数值模拟方法，一共设计了3种不同轴向偏转角的缝，开展缝式机匣处理及其轴向偏转角对跨声速轴流压气机稳定性改善的研究。本文拟达成以下两个研究目的：① 反叶片角向缝的扩稳机理；② 缝轴向偏转角的变化对其扩稳能力和扩稳机理的影响。

1 研究对象和数值模拟方法

1.1 研究对象

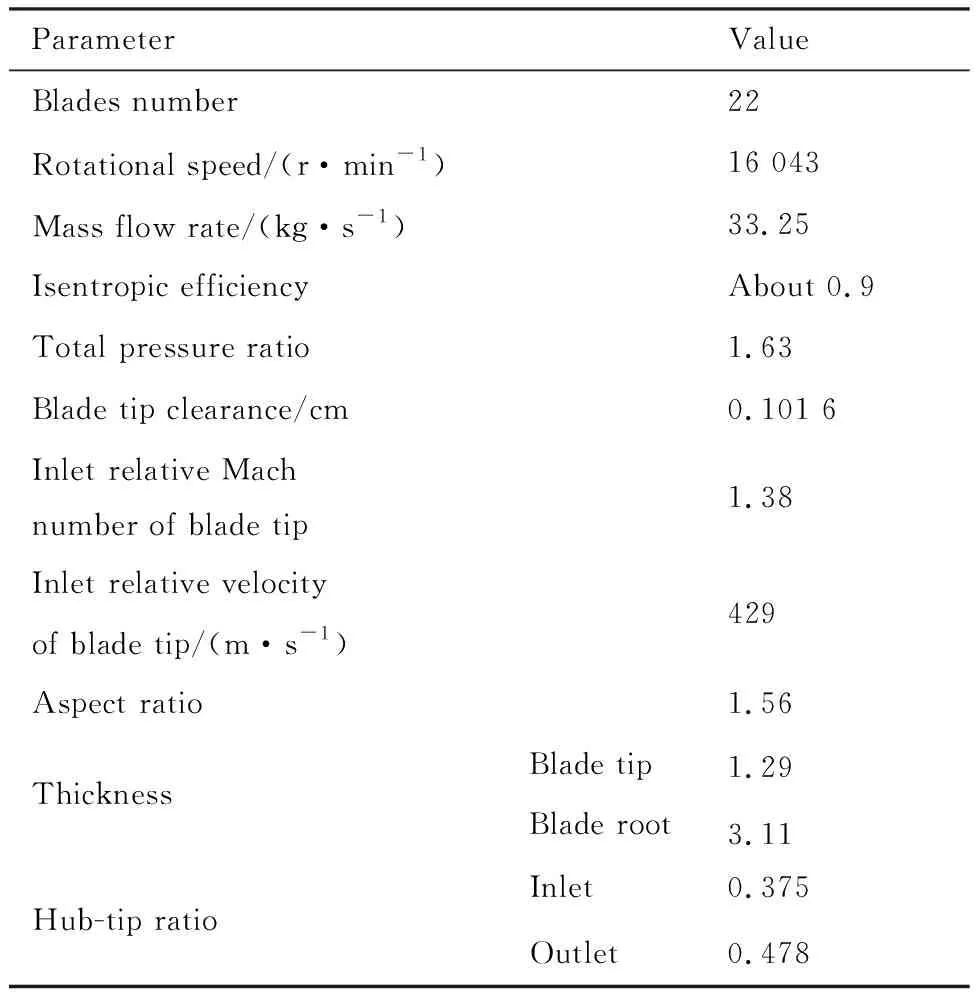
NASA Rotor 67是NASA为了研究展弦比对压气机性能的影响而设计的低展弦比跨声速进口级之一，NASA曾经对NASA Rotor 67的内部流场进行详细的测量，其最终结果于1989年9月发表在NASA的技术报告[18]中。图1为NASA Rotor 67的试验测量位置和数值模拟区域，图中A和R分别表示轴向和径向。表1和表2分别为NASA Rotor 67的基本设计参数和叶顶基元叶型参数。

为了揭示反叶片角向缝对跨声速轴流压气机稳定性的影响，并且澄清缝轴向偏转角的变化对其扩稳能力和扩稳机理的影响，本文一共设计了3种不同轴向偏转角的缝来进行机匣处理，即反叶片角向缝机匣处理(Reversed Blade Angle Slot Casing Treatment, RBASCT)、轴向缝机匣处理(Axial Slot Casing Treatment, ASCT)以及叶片角向缝机匣处理(Blade Angle Slot Casing Treatment, BASCT)，如图2所示。根据以往的研究经验和文献[14-15]可知，缝式机匣处理对叶顶通道气流进行抽吸和射流作用的动力是通过感受叶顶通道和叶顶吸/压力面的压差。为了使得3种缝均能够最大程度地感受这两个压差，以此获得最佳的扩稳效果，3种缝的轴向恰好覆盖叶顶前缘和尾缘、周向恰好横跨一个叶顶栅距(t)，3种缝的具体参数参见表3。缝长(L)的轴向投影(La)均为叶顶轴向弦长(ba)，缝宽(W)与缝片宽(w)之比均为1/1，缝宽(W)与叶型最大厚度(cmax)之比均为2.130 2/1，即开缝面积与处理面积之比(Open Area Ratio, OAR)均为50%，缝深(D)均为10%的叶顶弦长(b)，缝数(N)均为132，径向倾斜角(γ)均为0°，轴向偏转角(α)分别为负叶顶安装角-βy(反叶片角向缝，图2(a))、0°(轴向缝，图2(b))以及正叶顶轴向安装角+βy(叶片角向缝，图2(c))。需要说明的是，定义缝的走向沿着叶顶安装角的方向时缝的轴向偏转角为正。

图1 NASA Rotor 67试验测量位置和数值模拟区域Fig.1 Experimental measurement position and numerical simulation region of NASA Rotor 67

表1 NASA Rotor 67基本设计参数

Table 1 Basic design parameters of NASA Rotor 67

ParameterValueBlades number22Rotational speed/(r·min-1)16 043Mass flow rate/(kg·s-1)33.25Isentropic efficiencyAbout 0.9Total pressure ratio1.63Blade tip clearance/cm0.101 6Inlet relative Mach number of blade tip1.38Inlet relative velocity of blade tip/(m·s-1)429Aspect ratio1.56ThicknessBlade tipBlade root1.293.11Hub-tip ratioInletOutlet0.3750.478

表2 NASA Rotor 67叶顶基元叶型参数

图2 不同轴向偏转角缝的几何结构视图Fig.2 Geometric structure view of slots with different axial deflection angles

表3 不同轴向偏转角缝的几何结构参数

Table 3 Geometric structure parameters of slots withdeflection axial deflection angles

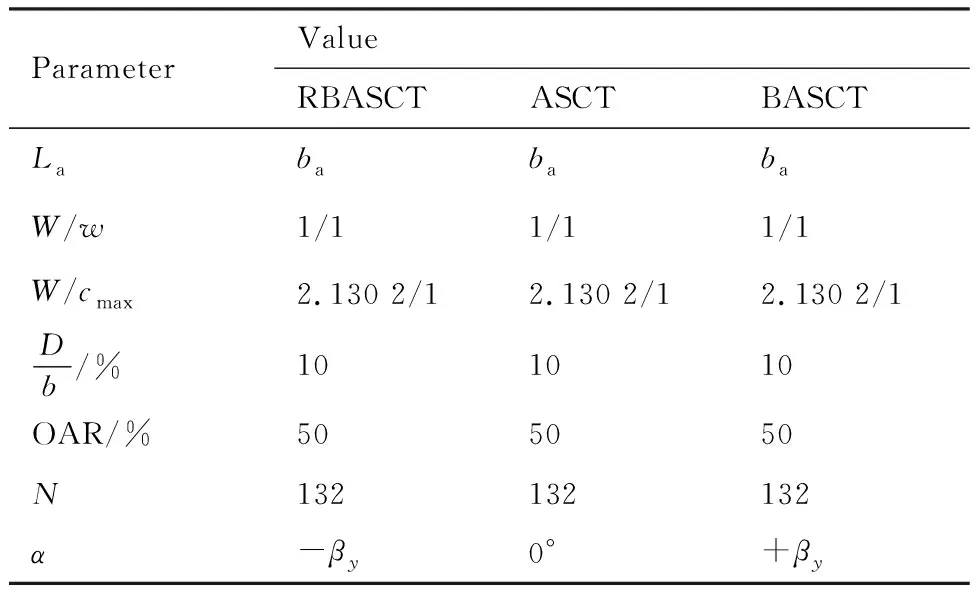
ParameterValueRBASCTASCTBASCTLabababaW/w1/11/11/1W/cmax2.130 2/12.130 2/12.130 2/1Db/%101010OAR/%505050N132132132α-βy0°+βy

1.2 数值模拟方法

本文利用NUMECA/FINE Turbo的EURANUS求解器对全三维雷诺时均Navier-Stokes方程在相对坐标系上进行求解。空间离散采用Jameson有限体积中心差分格式，并且选用适当的湍流模型。定常计算时选择显式四阶Runge-Kutta时间推进方法，并且采用多重网格法、当地时间步长以及隐式残差光顺等方法来加快收敛速度。非定常计算时利用隐式双时间步方法，并且压气机转过一个叶片通道的物理时间步设置为30、每2步保存一次，每个物理时间步下的虚拟时间步设置为20。为了减少计算时间，以相应的定常计算结果或者前一工况的非定常计算结果作为该工况非定常计算的初场。本文采用Spalart-Allmaras(S-A)、Spalart-Allmaras(Extend Wall Function)(S-A(EWF))、k-ε(EWF)以及Shear Stress Transport(EWF)(SST(EWF))4种湍流模型。

边界条件给定如下：进口边界条件根据试验给定绝对总温、绝对总压和绝对气流角(轴向进气)；出口边界条件给定出口的平均静压；叶片通道两侧定义周期性边界条件；机匣、轮毂以及叶片表面等固壁采用绝热无滑移边界条件。计算时上游段和缝式机匣处理设置为静止域，叶片通道、进口段、出口段以及下游段设置为转动域(如图3所示)。定常计算时转/静交界面的数据采用混合平面法处理；非定常计算时转/静交界面的数据采用Domain Scaling方法(两侧计算域面积相等)处理。

通过逐渐增加出口的平均静压获得压气机的总性能特性曲线，并且失速之前的最后一个工况对应着近失速工况，此时压气机出口的平均静压达到最大，计算中失速的定义与文献[19-21]中的一致：随着迭代步数的增加，压气机的流量、总压比以及等熵效率等性能参数不断减小直至收敛。

本文采用多块网格分区技术，叶片通道设置为HOH型网格拓扑。为了保证叶片前缘和尾缘附近的网格正交性，叶片采用O型网格拓扑。叶顶间隙采用蝶型网格拓扑(O型网格嵌套H型网格)并且保持叶顶间隙的几何形状不变。进口和出口延伸段均分解为两个网格块并且均采用H型网格拓扑，在叶片前缘和尾缘附近设置网格控制线，以保证叶片周围网格的密度和质量。3种缝均采用H型网格拓扑，其节点分布均为73×41×17(A×R×C，C为周向)。叶顶间隙和3种缝各自与一层很薄的滑移块进行非匹配连接，两层滑移块之间设为转/静交界面。图3为Grid 1的三维视图，其具体配置参见表4。

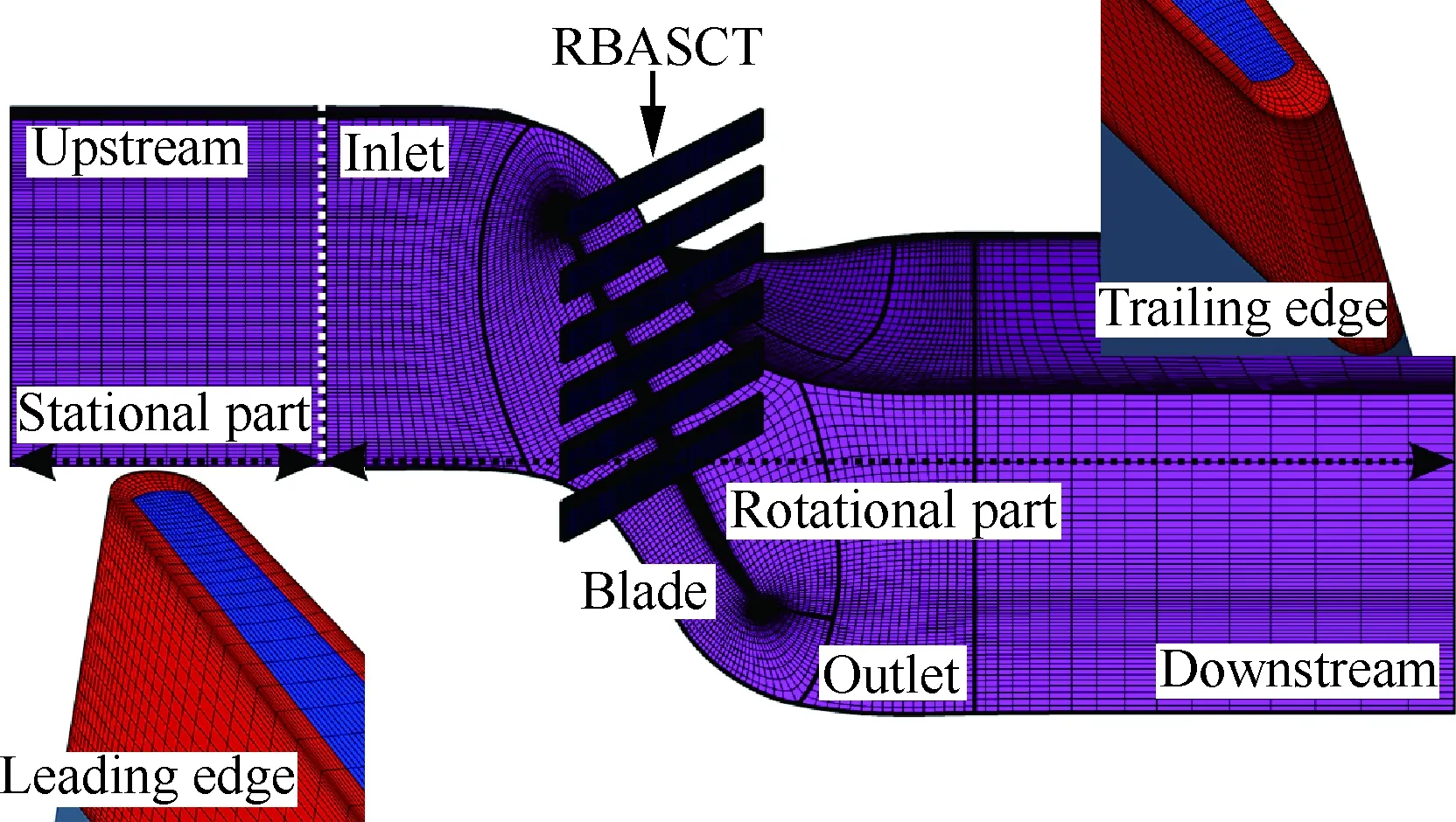
图3 Grid 1的三维视图Fig.3 Three-dimensional view of Grid 1

表4 网格的配置Table 4 Configuration of grids

GridBlade passage (O topology)Blade tip clearance (butterfly topology)Upstream/inletDownstream/outletCRACRACRACRA125105277933265173317757105179310517225121277949265174917757121179312117341105277933265173317757105179310517

本文设置Grid 1、Grid 2以及Grid 3这3套网格，单通道的总数分别约为180万、210万以及240万，3套网格的最小正交性均大于34°，最大长宽比均小于2 002，最大增长率均小于2.71。在3套网格中，Grid 1的总数和节点分布是参考文献[19]和根据数值模拟经验确定的，而Grid 2和Grid 3是在Grid 1的基础上沿着不同的方向增加节点数，目的在于验证Grid 1的合理性、即是否达到网格无关性的要求。分析表4可知，与Grid 1相比，Grid 2在周向和轴向的网格节点数保持不变，在径向增加16个网格节点，而Grid 3在径向和轴向的网格节点数保持不变，在周向增加16个网格节点。需要说明的是，在3套网格中，保证所有固壁附近的无量纲化网格高度y+均小于10。

1.3 试验校核

表5为采用不同网格和湍流模型时压气机计算(Cal)和试验(Test)得到的堵塞工况流量mb(时均值(Time AVerage, TAV))。分析表5可知，采用不同网格和湍流模型预测的结果均偏低、与试验值的相对误差(Relative Error, RE)均在-1%左右，表明采用不同网格和湍流模型均能较好地预测压气机的堵塞边界。

澄清实壁机匣时压气机的失稳机理是本文工作的一个重点，而预测缝式机匣处理对压气机稳定裕度的影响是本文工作的另一个重点，那么准确地预测压气机的近失速边界就显得尤为重要。

根据文献[18]，压气机近失速工况流量的试验值约为0.921 9(用堵塞工况流量进行无量纲化处理，下同)。表6为不同网格和湍流模型下压气机计算和试验的近失速工况流量ms(时均值)。分析表6可知，对于不同的网格，Grid 1、Grid 2以及Grid 3预测的结果分别约为0.923 7、0.924 1以及0.923 8，这与文献[18]的试验值符合良好。对于不同的湍流模型，S-A和S-A(EWF)预测的结果分别约为0.923 7和0.921 9，这与文献[18]的试验值符合良好，但是k-ε(EWF)和SST(EWF)预测的结果分别约为0.906 3和0.928 3，这与文献[18]中试验值的相对误差分别约为-1.692% 和0.694%，超过了文献[18]给定的误差范围，这就表明k-ε(EWF)和SST(EWF)不能准确地预测压气机的失速边界。

表5 不同网格和湍流模型下压气机堵塞工况的流量(时均值)

图4为近峰值效率点(Near Peak Efficiency，NPE)和近失速点(Near Stall，NS)下，采用不同网格和湍流模型时压气机计算和试验得到的测量站2处等熵效率沿叶高的分布(周向平均，时均值)。分析图4可知，在NPE和NS时，采用不同网格和湍流模型预测的结果在分布和量值上均与试验值吻合良好，均准确地反映了效率沿叶高的分布规律，并且不同网格和湍流模型之间预测的结果均相差很小。而NS时，采用不同网格和湍流模型预测的结果在量值上与试验值存在些许误差，集中在80%左右的叶高范围，具体表现在预测的效率高估了试验值，其最大绝对误差约为0.05。

综上所述，Grid 1已经达到网格无关性的要求，而k-ε(EWF)和SST(EWF)不能准确地预测压气机的近失速边界，相比于S-A，由于S-A(EWF)需要额外求解标准壁面方程，所需的计算时间和计算资源较多，因此，综合考虑计算效率和计算精度，本文采用Grid 1和S-A。为了进一步验证采用Grid1和S-A的准确性，也为了定性地衡量采用Grid 1和S-A捕捉压气机内部流场和激波的能力，图5给出了近峰值效率工况和近失速工况下，90%叶高处S1流面相对马赫数等值线的分布(时均值)，图中红色带箭头虚线指向相对马赫数等于1的等值线(近似表示激波)。分析图5可知，不同工况下，采用Grid 1和S-A预测的计算结果与试验数据吻合较好，不仅准确地捕捉了90%叶高处S1流面的流场，而且准确地捕捉了叶片通道的激波以及激波前后的相对马赫数数值。

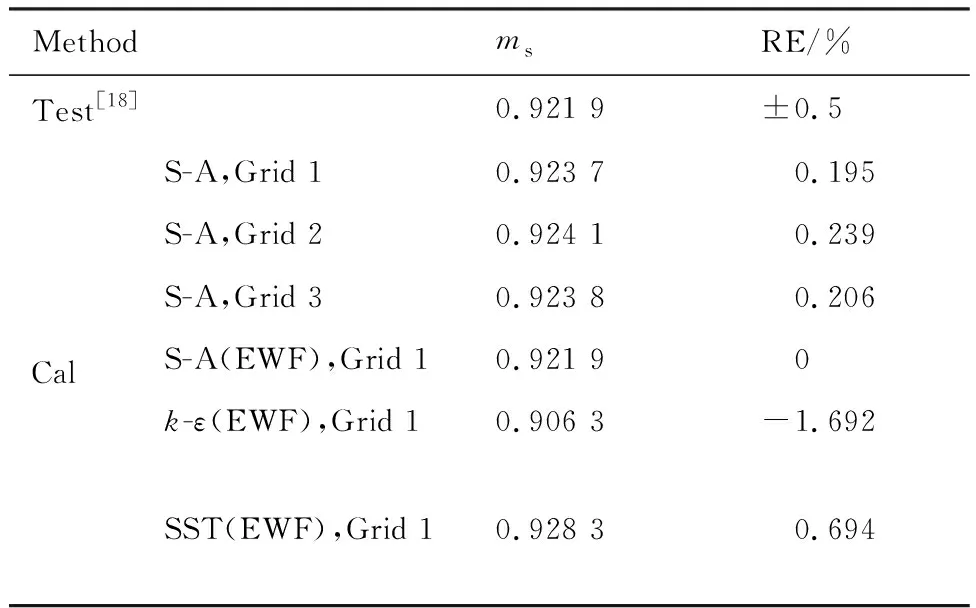
表6 不同网格和湍流模型下压气机的

图4 不同网格和湍流模型下压气机测量站2处等熵效率沿叶高分布(周向平均，时均值)Fig.4 Distribution of isentropic efficiency along blade span at Station 2 of compressor for different grids and turbulence models (circumferentially averaged, TAV)

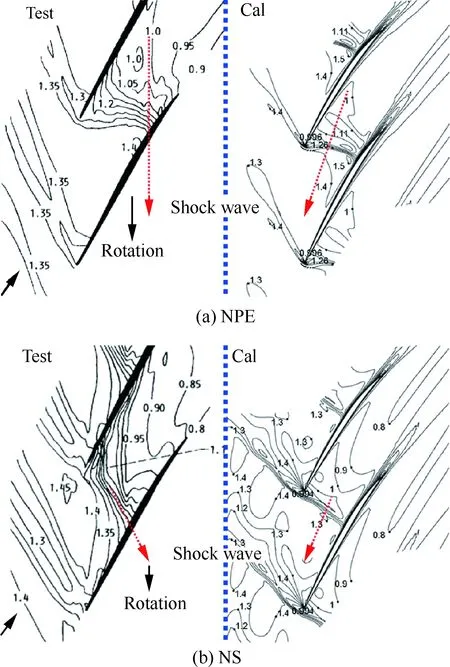
图5 90%叶高处S1流面相对马赫数等值线分布(时均值)Fig.5 Contours of relative Mach number on S1 stream surface at 90% blade span (TAV)

图6为实壁机匣时压气机计算和试验得到的总性能特性曲线(时均值)。图中SW(Solid Wall)表示实壁机匣。分析图6可知，在实壁机匣的全局流量范围内，计算的总压比和效率在分布上均与试验值符合良好，但是在量值上均存在些许差别，具体表现计算的总压比和效率均低估了试验值，其中计算的峰值效率与试验值的相对误差约为-3.11%。根据研究经验[20]，由于计算时引入绝热无滑移的边界条件，这将放大计算与试验之间的差异，并且网格和湍流模型的误差以及转/静交界面之间数据传递的误差等均会影响计算的准确性和精确度。为了消除上述顾虑，也为了进一步验证本文所采用的数值模拟方法的相对准确性，图6对比了南希[21]关于压气机的计算结果，对比分析可知，南希[21]的计算精度较高，相比之下，本文计算的近失速工况流量以及中小流量工况时的效率比南希[21]的更加接近试验值，这就验证了本文所采用的数值模拟方法的相对准确性。

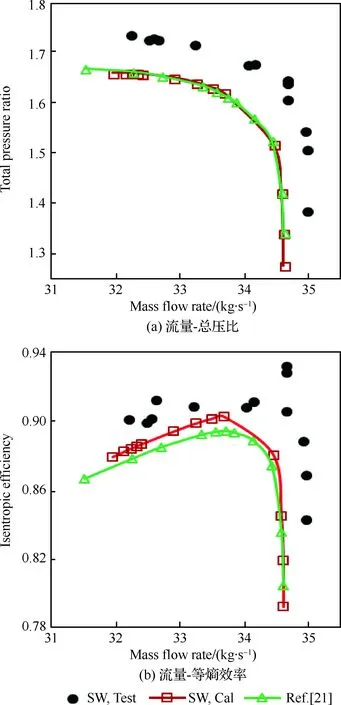
图6 实壁机匣时压气机的总性能特性曲线(时均值)Fig.6 Curves of total performance of compressor with solid wall casing (TAV)

2 结果与分析

2.1 总性能分析

图7为不同机匣时压气机的总性能特性曲线(时均值)。分析图7可知，与实壁机匣相比，加反叶片角向缝之后，反叶片角向缝在大中流量工况下降低了压气机的总压比和效率，在小流量工况下提高了压气机的总压比。随着缝的轴向偏转角由负向正变化，缝在全局流量工况下对压气机的总压比和效率的影响均很小。

图7 不同机匣时压气机的总性能特性曲线(时均值)Fig.7 Curves of total performance of compressor with different casings (TAV)

引进稳定裕度改进量(Stability Margin Improvement，SMI)指标和峰值效率改进量(Peak Efficiency Improvement，PEI)指标[22-23]，SMI和PEI分别用来衡量机匣处理对压气机稳定裕度和峰值效率的影响，其具体表达式分别为

(1)

(2)

式中：π*为总压比；m为流量；η*为等熵效率。下标“CT”代表机匣处理，“SW”代表实体壁机匣，“s”代表近失速边界点；“m”代表近峰值效率点。

表7为不同机匣时压气机的SMI和PEI(时均值)。分析表7可知，不同轴向偏转角的缝均提高了压气机的稳定裕度，但是均降低了压气机的峰值效率。反叶片角向缝获得的SMI和PEI分别约为24.22%和-1.19%。随着缝的轴向偏转角由负向正变化，缝的扩稳能力逐渐变弱，缝带来的峰值效率损失亦逐渐减少。

表7 不同机匣时压气机的SMI和PEI(时均值)

2.2 实壁机匣的失稳机理和反叶片角向缝的扩稳机理

下面对比分析实壁机匣和反叶片角向缝时压气机处于相同流量工况的内部流场，其中压气机处于实壁机匣时的近失速工况。

图8为98.5%叶高处S1流面静压等值线、相对速度矢量以及叶顶间隙泄漏流的分布(时均值)。图中红色实线为相对马赫数等于1的等值线、近似表示激波的位置和形状，红色带箭头实线为气流的方向，黑色带箭头虚线表示泄漏涡，泄漏流的速度大小为相对速度Wxyz与叶顶进口相对速度W1之比。分析图8可知，①实壁机匣时，泄漏流向相邻叶片压力面前缘扩散并且形成低速区，低速区的气流以近似垂直于相邻叶片压力面前缘的方向流向叶片通道下游，由泄漏流卷起形成的泄漏涡明显偏离吸力面，激波被推出叶片通道，近似与前缘对齐。结合Vo[24]和Wilke[25]等的研究可知，此时压气机的失速类型为叶顶堵塞形式的突尖型失速。②加反叶片角向缝之后，泄漏流及其卷起的泄漏涡均偏向吸力面，偏转角度约为5.82°，泄漏流集中地围绕在泄漏涡涡核的周围，叶片通道不存在低速区。吸力面后半段的泄漏流出现中断，吸力面前半段的泄漏流速度明显提高，这是反叶片角向缝对泄漏流进行抽吸和射流作用的结果。

为了进一步描述反叶片角向缝对叶顶通道气流的抽吸和射流作用。图9给出了不同时刻叶顶间隙泄漏流和反叶片角向缝开口面静压系数Csp及其中间截面相对速度矢量的分布。图中蓝色虚线方框标记鞍点，τ和T分别表示时刻和压气机转过一个栅距所需要的时间。图中选取5个典型时刻的计算结果进行分析并且不同时刻的时间间隔一致。Csp的定义为

图8 98.5%叶高处S1流面静压等值线、相对速度矢量以及叶顶间隙泄漏流的分布(时均值)Fig.8 Distribution of static pressure isolines, relative velocity vector and blade tip clearance leakage flow on S1 stream surface at 98.5% blade span (TAV)

(3)

式中：psp为静压；pref为参考静压，取标准大气压力；ρ为密度。

分析图9可知，在叶片通道和叶顶吸/压力面压差的作用下，不同时刻、反叶片角向缝中间截面的气流整体呈现顺时针循环流动，在后端进行抽吸作用、而在前端进行射流作用，或者在压力面侧进行抽吸作用、而在吸力面侧进行射流作用，其右上角的气流却呈现逆时针循环流动。

分析图9还可知，① 反叶片角向缝同时跨过两个叶顶时(T/15→4T/15)，由于缝同时利用两个叶顶吸/压力面的压差，中间截面的气流流动较为复杂，沿着后端向前端方向，抽吸和射流作用交替分布。气流在其右上角的逆时针循环流动在T/15时刻形成回流区，而在4T/15时刻没有形成回流区。② 反叶片角向缝仅仅跨过单个叶顶时(7T/15→10T/15→13T/15)，由于缝仅仅利用单个叶顶吸/压力面的压差，中间截面的气流流动较为简单，在后端进行抽吸作用、而在前端进行射流作用，其分界点逐渐向叶顶移动。而7T/15时，由于中间截面的下端中部存在回流区，此时的分界点位于回流中心。气流在其右上角的逆时针循环流动均形成回流区，并且在回流区的右下角均出现类似鞍点的流动现象。结合图8(b)的分析可知，缝的抽吸作用抽走了吸力面后半段的泄漏流，缝的射流作用激励了吸力面前半段的泄漏流，这两者的共同作用消除了叶顶通道内部由泄漏流及其泄漏涡扩散导致的堵塞。

图9 叶顶间隙泄漏流和反叶片角向缝开口面静压系数及其中间截面相对速度矢量的分布Fig.9 Distribution of blade tip clearance leakage flow, static pressure coefficient on open face and relative velocity vector at mid-section for RBASCT

2.3 缝轴向偏转角的影响

下面对比分析不同轴向偏转角的缝时压气机处于相同流量工况的内部流场，其中压气机处于实壁机匣时的近失速工况。

图10为4T/15时刻叶顶间隙泄漏流和缝开口面静压系数Csp及其中间截面相对速度矢量的分布。分析图9(b)和图10可知，随着缝的轴向偏转角由负向正变化，由于缝从同时跨越两个叶顶逐渐变成仅仅跨越单个叶顶，即从同时利用两个叶顶吸/压力面的压差逐渐变成仅仅利用单个叶顶吸/压力面的压差，中间截面气流流动的复杂程度逐渐减弱，在后端进行抽吸作用、而在前端进行射流作用，其分界点逐渐向叶顶移动。而轴向缝时，由于中间截面的下端中部存在回流区，此时的分界点位于回流中心。

图11为叶顶间隙泄漏流的流动特性和基元载荷沿叶高的分布(时均值)。图11(a)和图11(b)分别为叶顶间隙泄漏流的速度大小和相对总压系数Crtp沿叶顶轴向弦长的分布，由于不同轴向偏转角缝的作用范围集中在叶顶区域，图11(c)仅仅给出55%～100%叶高范围的基元载荷(L)。图11(a) 中黑色虚线矩形方框表示不同轴向偏转角缝的轴向覆盖范围。Crtp和L的定义分别为

图10 叶顶间隙泄漏流和缝开口面静压系数及其中间截面相对速度矢量的分布(τ=4T/15)Fig.10 Distribution of blade tip clearance leakage flow, static pressure coefficient on open face of slots and relative velocity vector at mid-section (τ=4T/15)

(4)

图11 叶顶间隙泄漏流的流动特性和基元载荷沿叶高的分布(时均值)Fig.11 Characteristics of blade tip clearance leakage flow and distribution of element load along blade span (TAV)

式中：prtp为相对总压。

(5)

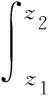
式中：pps为压力面静压；pss为吸力面静压；rps为压力面半径；rss为吸力面半径；z为轴向坐标；z1和z2分别为叶顶前缘和尾缘的轴向位置。

分析图11可知，根据Wilke和Kau[14]的研究，实壁机匣时，随着压气机向近失速边界节流：在整个叶顶轴向弦长范围之内，泄漏流的速度大小和相对总压均逐渐降低；在较高叶顶范围之内，叶片通道的逆压梯度逐渐增强，即叶片的基元载荷逐渐减加；这就导致泄漏流的总压损失逐渐增加以及叶片的做功能力逐渐增强。加反叶片角向缝之后，泄漏流的速度大小和相对总压沿着整个叶顶轴向弦长均明显提高，叶片的基元载荷也明显增加。结合图8～图9的分析可知，反叶片角向缝的抽吸和射流作用提高了泄漏流的驱动力，减少了泄漏流的总压损失，增强了叶片的作功能力。

随着缝的轴向偏转角由负向正变化，泄漏流的速度和相对总压在叶顶轴向弦长的前半段逐渐降低、在叶顶轴向弦长的后半段逐渐提高，叶片的基元载荷在55%～80%的叶高范围增加、在80%～100% 的叶高范围减少，并且在85%～100%的叶高范围低于实壁机匣。造成上述变化的原因在于：随着缝的轴向偏转角由负向正变化，缝从同时跨越两个叶顶逐渐变成仅仅跨越单个叶顶。在叶顶轴向弦长的前半段，缝能够利用的叶顶载荷逐渐减少、即泄漏流的驱动力逐渐减弱，这就导致泄漏流的速度大小和相对总压逐渐降低；在叶顶轴向弦长的后半段，缝能够利用的叶片流道压差逐渐增强，这就导致泄漏流的速度大小和相对总压逐渐提高；而在较高叶顶范围，缝能够利用的叶顶载荷减少，这就导致叶片的基元载荷逐渐减少。

为了进一步定量地说明不同轴向偏转角的缝对叶顶通道气流的抽吸和射流作用。图12为不同轴向偏转角的缝开口面抽吸量mB、射流量mI和机匣处理效率随着时间的变化情况。抽吸量和射流量均用压气机近失速工况的流量进行无量纲化处理。本文将通过不同轴向偏转角的缝开口面的气流分为两部分，其中Wr>0(Wr为相对速度径向分量)的部分气流(即从叶顶通道进入缝的气流)定义为缝的抽吸气流，而Wr<0的部分气流(即从缝进入叶顶通道的气流)定义为缝的射流气流。而缝抽吸和射流的流量通过对缝的开口面(S)进行积分获得，即：

图12 缝开口面气流流动特性Fig.12 Characteristics of airflow on open surface for slots

(6)

式中：下标“B”和“I”分别代表抽吸与射流作用。

根据王维[26]的研究，定义机匣处理的效率E为其开口面射流量与抽吸量的比值，即E=mI/mB，机匣处理的效率可以间接反映机匣处理的扩稳能力及其对压气机效率的影响。

分析图12可以发现，在抽吸量方面，反叶片角向缝的最大，轴向缝和叶片角向缝的次之并且二者基本相等。在射流量方面，反叶片角向缝和叶片角向缝的最大并且二者基本相等，轴向缝的次之。在机匣处理效率方面，叶片角向缝的最大，反叶片角向缝的次之，轴向缝的最小。

结合图9和图10的分析可知，不同时刻、不同轴向偏转角的缝内均存在不同范围回流区(如图9(c)～图9(e)中反叶片角向缝右上角的逆时针回流区以及图10(a)中轴向缝下端中部的回流区)，缝的后端对叶顶通道气流的抽吸作用将叶顶通道的部分气流抽入缝内，理想情况下，这部分气流将通过缝的射流作用全部从缝的前端射入叶顶通道，但是由于缝内存在的各种回流消耗了一部分抽吸气流，这就导致射流气流小于抽吸气流。这就是说图12(c)中机匣处理效率的物理内涵就是衡量机匣处理对抽吸气流的实际转换率。总的来说，机匣处理的内部流动符合质量和流量守恒，即抽吸量=射流量+缝内回流量，这就可以解释在一个叶片通道通过周期之内，不同轴向偏转角缝的效率均低于100%的原因是，缝内回流消耗了一部分抽吸气流。

总的来说，通过感受叶片通道和叶顶吸/压力面的压差，反叶片角向缝通过对泄漏流进行抽吸和射流作用，一方面消除了泄漏流及其泄漏涡扩散带来的负面影响，另一方面激励了泄漏流，提高了泄漏流的速度，降低了泄漏流的总压损失，增强了叶片的做功能力。根据文献[22-23]的研究可知，缝的抽吸和射流作用会与叶顶通道的主流产生掺混损失，缝内的回流也会产生回流损失，这两者的共同作用会降低压气机的效率。

根据不同轴向偏转角的缝与叶顶的相对位置(参见图2)可知，随着缝的轴向偏转角由负向正变化，其开口面逐渐向叶顶安装角的方向偏转。一方面，这将减弱缝感受叶顶吸/压力面压差的能力，进而降低其对叶顶通道气流的抽吸量和射流量，从而减弱其扩稳能力。另一方面，这将减小其由于抽吸和射流作用带来的掺混损失，并且缝内的回流损失也将减小，从而减少压气机的效率损失。

结合本文以及王维[26]的研究可知，针对某些压气机，运用机匣处理效率可以衡量机匣处理的扩稳能力，但是对于本文的研究对象，机匣处理效率越高对应的机匣处理扩稳能力不一定越强，这就说明不同压气机的叶顶载荷不一样，极有可能造成机匣处理效率的变化与机匣处理扩稳能力的变化不一致。加机匣处理之后，压气机叶顶流场的三维效应更加明显，各种流动的相互作用更加复杂，对于不同的压气机，很难依靠某个公式同时衡量机匣处理的扩稳能力及其对压气机效率的影响。但是结合相关文献[5-6, 12-13]的研究可知，机匣处理的扩稳能力及其对压气机效率的影响是其抽吸量和射流量共同作用的结果，机匣处理的抽吸量和射流量越大、其扩稳能力越大，但是带来的掺混损失和回流损失也越大、即压气机的效率损失越大，反之亦然。根据图12的分析可知，反叶片角向缝的抽吸量和射流量最大、轴向缝和叶片角向缝的次之，这就可以验证表7有关不同轴向偏转角的缝对压气机SMI和PEI的影响，同时也符合Takata和Tsukuda[11]的研究结果。