浅谈转化思想在小学数学“图形与几何”中的运用
2018-08-28朱小花
朱小花
摘 要:转化思想主要表现为数学知识的某一种形式向另一种形式的转变。教材中渗透转化思想的教学内容主要集中在平面图形与立体图形的转化;三角形内角和和多边形内角和公式的推导;正方形、平行四边形、梯形、三角形、圆面积公式的推导;立体图形表面积、侧面积和体积公式的推导等,文章主要从以上方面进行阐述。
关键词:转化思想;小学数学;“图形与几何”;运用
中图分类号:G623.5 文献标识码:A
一、平面图形与立体图形的转化
新课程标准把平面图形与立体图形的转化作为图形认识的一个重要内容,这有利于初步培养学生的空间观念。第一学段的要求是辨认从正面、侧面、上面观察到的简单物体的形状。第二学段要求能辨认从不同方位看到的物体的形状和相对位置通过观察、操作,认识长方体、正方体、圆柱和圆锥。教材中观察物体这一内容就是将立体图形转化为平面图形的集中体现,从二年级到六年级的各册教材中均有涉及,从具体到抽象,采用逐步渗透、深化、螺旋上升的方式依次呈现。
二、三角形内角和和多边形内角和的推导
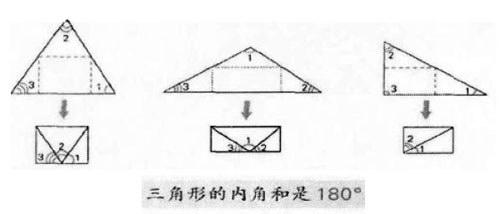
1.三角形内角和的推导
研究三角形内角和时,把三角形的内角和转化成一个平角来证明三角形的内角和是180度,初步渗透了转化思想。
2.多边形内角和公式的推导
学生在学习探索多边形的内角和的时候,已学习了三角形内角和定理、三角形相关知识,在前面特殊四边形性质的探索过程中,也体会了转化思想在解题中的应用,具备了进一步学习的基础。随着几何知识学习的逐步深入,学生掌握了一定的解决几何问题的方法,多边形内角和定理的探索,需要学生结合图形发现规律。推导多边形内角和公式的方法是将多边形分割为多个三角形,将多边形的内角和转化为我们所熟知的三角形内角和来解决。可以归纳总结出n边形内角和为(n-2)×180°。
三、正方形、平行四边形、梯形、三角形、圆面积公式的推导
正方形的面积:把正方形看作长和宽相等的长方形。
平行四边形的面积:通过割补、平移转化成长方形。
梯形的面积:把两个完全相同的梯形,通过旋转、平移转化成平行四边形。这个平行四边形的底等于梯形的上底加下底,高与梯形的高相等。梯形面积是拼成的平行四边形面积的一半。
三角形的面积:把两个完全相同的三角形,通过旋转、平移转化成与它等底、等高的平行四边形。一个三角形的面积是拼成的平行四邊形面积的一半。
圆的面积:把一个圆平均分成若干份后,拼成一个近似的长方形。长方形的长相当于圆周长的一半,宽相当于圆的半径。
四、立体图形表面积、侧面积和体积公式的推导
(1)长方体的表面积:将立体图形想象成平面图形进行计算,将计算长方体的表面积转化成计算长方体六个面的面积之和。
(2)圆柱的侧面积:将圆柱沿着高展开,展开后的形状是长方形,这样就将计算圆柱的侧面积转化为计算长方形的面积。
(3)圆柱的体积:圆可以转化成长方形计算面积,圆柱可以转化成长方体计算体积。把圆柱的底面积平均分成若干份,切开后拼成了一个近似的长方体。这样计算圆柱的体积就转化为了计算长方体的体积。
五、结语
“转化思想”是数学思想方法的一种重要方法,它可以帮助我们将数学问题化繁为简,化难为易,化未知为已知,贯穿小学数学教材,“图形与几何”教学宜采用直观的方法渗透转化思想。教师应从低年级开始逐渐渗入,为学生“转化思想”的形成打好基础,而教师的教学中同样需要“转化思想”,不仅在对学生的教法上要运用“转化思想”,求变求新,还应对自身教学的态度运用“转化思想”,明确教学的首要目标。
参考文献:
[1]徐国莲.谈数学思想方法在教学中的渗透[J].保山师专学报,2006(5).
[2]赵红星,王汉超.转化思想在解题中的应用[J].中学数与学,2001(10).
