基于电池交换的电动汽车充电设施规划方法研究
2018-08-28顾腾飞张勇
顾腾飞,张勇
(苏州大学轨道交通学院,江苏 苏州 215131)
电动汽车续航里程短、充电时耗长、充电设施不普及等因素限制了其推广应用。电动汽车充电方式主要有两类,一类是整车充电;另一类是电池交换,即在换电站将电能耗尽的电池取下,换上满电电池。后者补能迅速,是潜力较大的充电方式。
电池交换方式的补能基础设施研究主要有两类,一是换电站布设研究;二是换电站内充电桩及电池配置的研究。在第一类研究中,Mak等[1]建立了成本最低和实现投资收益目标概率最大两个选址模型,后者能更快地给出选址方案,但没讨论电池容量的选择问题。为此,Nie等[2]以社会总成本最小为目标建立模型研究电池容量和充电功率的选择,但该研究未考虑电池交换需求是路径选择的结果。而Yang等[3]用整数规划模型来研究换电站站点设置和车流路径选择问题,并进行经济和环境影响分析。此外,钱斌等[4]利用近邻传播聚类方法优化电池交换式电动公交的充电站址,再以建设成本最小为目标,给出充电桩、换电位和电池保有量的规划方案。该模型适用于电动公交。而面对出租车的换电需求,Wang等[5]以所有换电需求的总时间成本最小为目标建立模型,给出了换电站布设方案,并利用苏州出租车现状进行案例分析。Jamian等[6]还从减少配电网电能损失的角度研究换电站布设问题,利用分析法和人工蜂群算法分别给出了电能损失最小的方案。Kang等[7]面对用电价格波动提出电池交换式电动汽车的集中充电策略,并优化了充电地点和充电规则,在换电站布设完成后,需进一步研究站内充电桩、电池保有量等问题。因此,在第二类研究中,Adler等[8]设计了一种车辆引导模型,解决电动汽车网络导航和电池储备问题。相对于普通电动汽车,电动公交的换电需求更为频繁,因而Zou等[9]研究电动公交换电站配置优化问题,以运营成本最小为目标建立模型,优化站内充电桩及电池数量,并对北京换电站进行案例分析。Wu等[10]以日间电池保有成本最小为目标建立规划、运营两阶段模型,并以香港国际机场公交进行案例分析。
上述研究存在两个缺陷。首先,以往研究忽略了充电过程,而认为总是有电池可换。而卸下的电池在站内也有较长的充电过程,若保有电池数较少,会出现无法立刻换取满电电池的情况,因而不能将其忽略。其次,站点配置的电池数不仅与充电时间相关,还与运营商所担保的能立刻换得满电电池的概率(下文称换电成功概率)相关。针对以往研究忽略了的这两个因素,本文做了以下研究:(1)为描述充电过程,基于生灭过程理论,建立电池满电或缺电状态数学描述;(2)以充电设施建设成本最小为目标,考虑换电成功概率要求,建立换电站及保有电池数决策模型;(3)采用构造拉格朗日函数的方法,对决策模型提出求解算法。通过以上分析,利用所建的模型及其求解算法,结合算例,揭示换电成功概率、充电速率对建设成本的影响。
1 基本模型
1.1 电池交换过程及基本假设
研究道路长为S,该道路上均匀分布m个间距为l的换电站。有补能需求的电动汽车到达后,换取满电电池,耗尽的电池留在换电站充电并供后续到达的电动汽车换取。图1展示了电池交换及电池充电的过程。
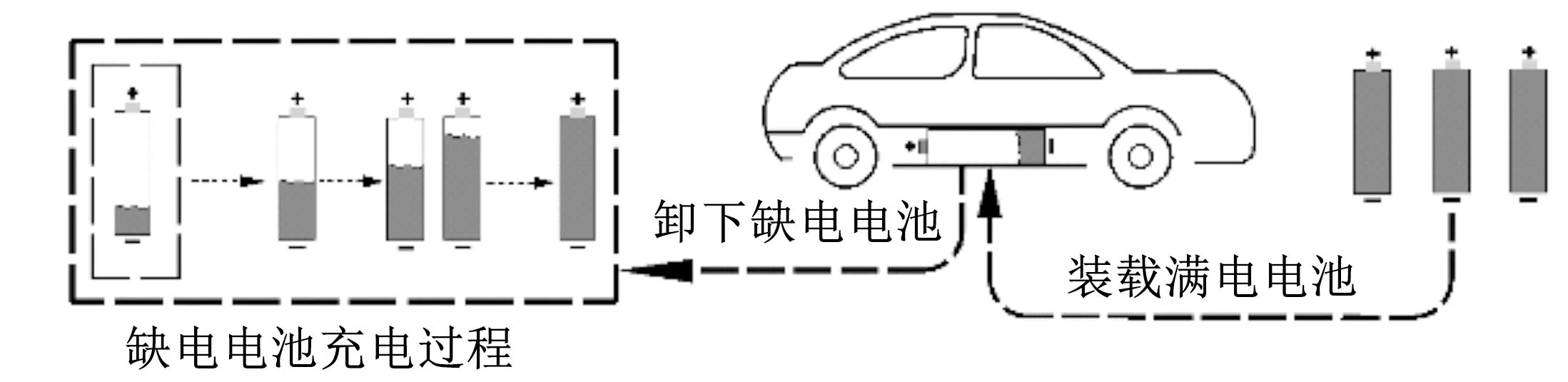
图1 电池交换示意图Fig.1 Battery-swapping of electric vehicles
为方便建模,进行如下假设:
(i)对于第i个换电站,电动汽车的到达服从参数为αi的泊松分布;
(ii)待充电池的充电时间服从参数为μ的负指数分布;
(iii)满电电池续航里程应大于相邻站点间距;
(iv)道路上设置的换电站是等间距的;
(v)电池是统一标准的,即满电电池续航里程相同;
(vi)仅考虑单方向情况,单位时间单位距离上产生的需求为β(x),β(x)是关于具体位置x的函数。
1.2 模型构建
1.2.1 需求分析

换电站个数应大于站间距个数,则:
(1)
根据假设(iii),电池续航里程大于站间距,则有:
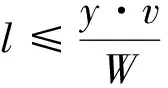
(2)
其中,y为电池的电量,v为车速,W为电池功率。
根据公式(1)、(2),易得:
(3)
根据图2,考虑从站1到站m方向的交通量对沿途换电站换电需求的影响,此时则有:
αi=λ1·(f1i+f1(i+1)+f1(i+2)+…+f1m)+λ2·(f2i+f2(i+1)+f2(i+2)+…+f2m)+…+λi。
(4)
另外,设施总服务速率应大于换电需求到达率,因此有:
。
(5)

图2 道路沿线站点布置Fig.2 Layout of stations along the road
1.2.2 交换站状态转移过程分析
由1.1假设(i)、(ii)知,电动汽车的到达服从参数为αi的泊松分布,待充电池的充电时间服从参数为μ的负指数分布。若将电车上卸下的待充电池看成系统的顾客,那么每到达一辆电动汽车,就会卸下一块电池等待充电,这个速率和电车的到达率αi是一致的,泊松流的到达间隔时间服从负指数分布,因此待充电池的“到达”时间间隔亦服从负指数分布。而待充电池随着充电的进行将会被充满,每充满一块电池就意味着一个“顾客”——待充电池的离开,这个速率与单服务台充电速率μ及此时正在充电的电池数有关。整个过程都伴随着待充电池的“到达”和“离开”,因此,根据随机过程理论,换电站的状态转移过程本质上为一个生灭过程。但值得注意的是,一辆电动汽车到达后,如果换电站此时有满电电池,那么将会换取一块电池并即刻离开;如果没有满电电池,将会在换电站处排队等待,因此用(b,v)表示电池交换站状态,b、v分别代表可用于交换的满电电池数、系统中电动汽车数。设换电站i保有的电池数量为Ni,则第i个电池交换站的电池状态转换如图3所示。

图3 电池交换站可用电池状态转换Fig.3 The state transition of full batteries in battery-swapping stations
将换电站内部电池和电车状态变化情况分成三部分来看:
第一部分是端点情况。如图4所示,当电池交换站状态为(Ni,0)时,换电站有Ni块可交换电池,没有电车在等待,此时换电站状态只能以αi的速率向(Ni-1,0)状态转化。

图4 端点状态变化情况Fig.4 The transition of endpoint states
第二部分是有可交换的满电电池的情况。此时系统内没有电动汽车等待,如图5所示。当系统状态为(b,0)时,瞬时可以向两种状态转化:(1)当前有(Ni-b)块电池正以速率μs转化为(b+1,0)状态;(2)每到达1辆电动汽车就有1块充满电的电池将被换走,即以速率αi向(b-1,0)状态转化。

图5 存在可交换电池的状态变化情况Fig.5 The state transition of situations which contain swappable batteries
第三部分是电池全部在充电的情况。此时系统内有电动汽车等待,如图6所示。当系统状态为(0,v)时,瞬时可向两种状态转化:(1)当前有Ni块电池正以速率μs向满电电池转化,每充满一块电池就有一辆电动汽车成功换电离开,即系统以Ni·μs的速率向(0,v-1)状态转化。(2)每到达1辆电动汽车就意味着增加一辆排队等待的电动汽车,即系统以αi的速率向(0,v+1)状态转化。

图6 存在电车等待换电情况下的状态变化Fig.6 The state transition of situations which contain waiting vehicles
由此可见,换电站状态转移概率与到达率αi、充电速率μ、换电站总的保有电池数Ni和此时电池交换站状态(b,v)有关。综上所述,在稳态的情况下,可得下列表示各种状态间相互转移的差分方程:
(6)
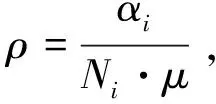
。
(7)
(8)
(9)
令p0表示无满电电池可以更换的概率,则:
。
(10)
当电动汽车到达换电站时,并不意味着立刻就能换到电池。令η为电动汽车能立刻换得满电电池的最小概率(下文简称换电成功概率),则换不到电池的概率不应大于1-η。即在电池交换站处无可交换电池的概率应满足式(11)。
(11)
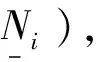
1.2.3 换电站及其保有电池规划
针对电池容量可变情形,建立换电站及其配置电池的优化模型。电池容量决定其采购成本,假设电池价格与容量是线性关系,即:K(y)=a+b·y。其中,a为电池基价,b为单位电池容量价格。假设每个换电站建设成本为c,则建设总成本C为:

(12)
其中,决策变量包括电池容量y、配置电池数Ni以及换电站数m。以建设总成本最低为目标,根据约束条件(3)、(4)、(5)和(11),得下述优化模型:
(13)
st.
(14)
2 求解算法
本文采用构造拉格朗日函数的方法,寻求规划问题的K-T点,运用K-T条件和约束条件建立方程组,并讨论乘子的取值以确定最优性条件。针对模型(13)、(14),构造拉格朗日函数如下:
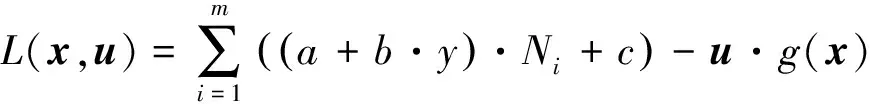
(15)
其中:
x为决策变量,u为拉格朗日乘子,g(x)是约束条件函数组成的向量。对x求偏导∂L(x,u)/∂x,并根据K-T条件和约束得下列方程组:
(16)
式中,ni表示换电站i应保有的最少电池数量。由式(16)得:
(17)
求解式(17)中的ni是本算法的关键,为此可利用公式(11)结合具体参数进行求解。
3 算例分析
3.1 算例设置
设道路长度S为800 km,v=60 km ·h-1,W=15 kW,c=300万元,电池价格与容量的关系为:K(y)=3 500·y+ 10 000。单位时间内每公里路段产生的需求量β(x)=0.2次/(km·h);换电站充电速率μ=2块·h-1。
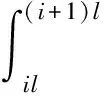
。
(18)
3.2 充电设施建设成本分析
3.2.1 不同建站情况设计要求
该模型是以换电站及其配置的电池数为决策变量的整数规划问题,这类问题难以解决。幸运的是,道路上换电站数量是有限的。因此,可通过枚举并比较不同建站数对应的目标函数(13)的值来求解。
在给定参数下,可算得换电系统设计要求,如表1所示。据表1知,建站数较少时,站间距、基本吸引量较大,因此需要配置的电池容量也较大,电池组价格相应较高;反之,站间距、基本吸引量及相应的电池容量、价格则较小。因此,有必要寻求最优的换电站数量及配置的电池数组合,确保满足换电成功概率约束下的建设成本最小化。

表1 建不同数量换电站的设计要求Table 1 Design requirements for the construction of different number of battery-swapping stations
由式(17)得各种建站情况下各站点总需求率:
(α1,α2,α3)=(54,90,90);
(α1,…,α4)=(40,70,80,70);
(α1,…,α5)=(32,57.6,70.4,70.4,57.6);
(α1,…,α6)=(27,49.5,63,67.5,63,49.5);
(α1,…,α7)=(23,42.7,55.9,62.4,62.4,55.9,42.7);
(α1,…,α8)=(20,37.5,50,57.5,60,57.5,50,37.5);
(α1,…,α9)=(18,34,46,54,58,58,54,46,34)。
3.2.2 保有电池数对换电成功概率影响
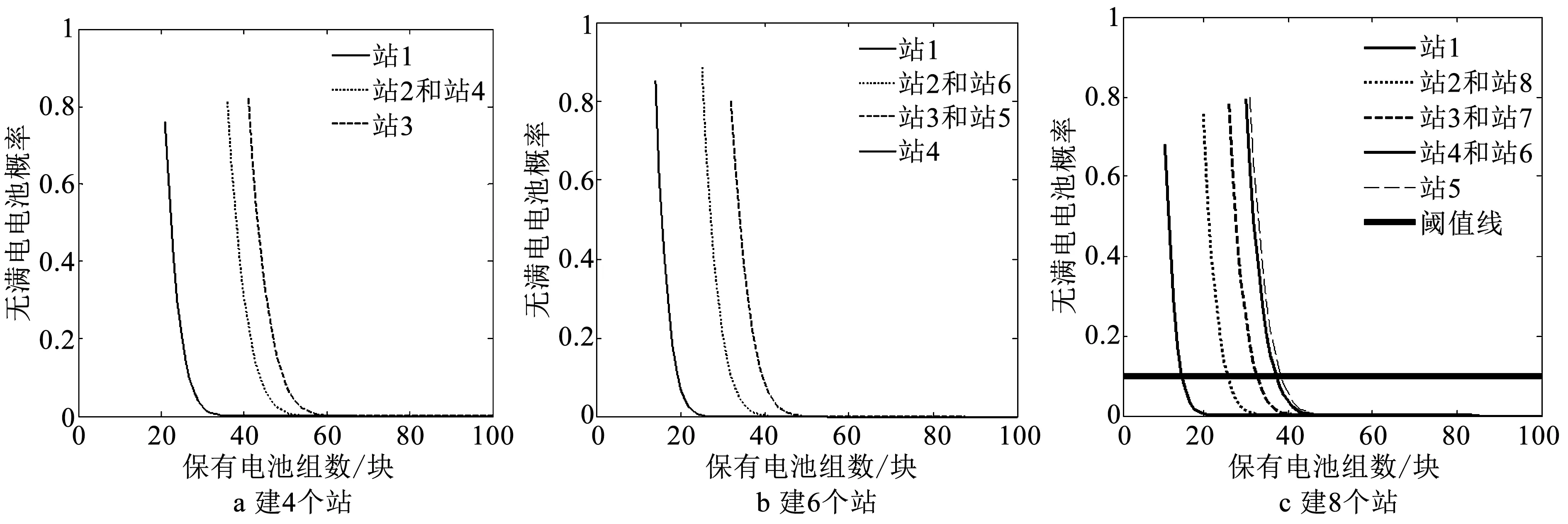
图7 无满电电池概率与站点保有电池数关系图Fig.7 Relationship between the number of batteries and the probability of no swappable batteries
电动汽车用户最为关心的是到达站点后能否立刻换到电池,其概率很大程度上取决于换电站保有电池数。据式(11)可算得电动汽车到达后无满电电池可换的概率。图7a~c展示了不同建站数情况下(仅展示部分建站情况),各站保有电池数与无满电电池概率之间的关系。从图中可以看出,换电站无满电电池概率关于Ni是单调递减的,即换电站配置电池越多,换电成功概率越大。运营商需将不能立刻换得满电电池的概率控制在一个较小值(称阈值)内。以图7c中建8个站为例,阈值线与无满电电池概率曲线的交点,即为该站所需保有的最少电池数,阈值为0.1时,站1至少应保有16块电池。
3.2.3 换电成功概率对建设成本的影响
换电站所设定的换电成功概率影响其配置的电池数,进而影响总建设成本。通过计算可得换电成功概率对整个系统保有的最少电池总数、综合建设成本的影响,如图8、9所示。据图8、9知:(i)同样建站数下,要求的换电成功概率越高,规划的最少电池数越多,总建设成本越大;反之,只需保有较少的电池数,但可能产生排队,因而违背了换电站高效的原则。(ii)换电成功概率η=0.9时,仅从电池数上看(如图8所示),建3个站似乎是最优的,但图9显示建4个站总建设成本反而更低。原因是电池单价不同,影响了电池组保有成本进而影响总建设成本。因此,在规划充电站及其配置电池数时,不能仅依据换电站及电池数量,还需考虑站点建设成本及电池容量-价格关系。
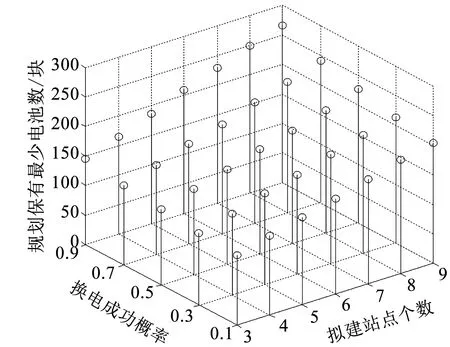
图8 换电成功概率对规划保有的最少电池数的影响Fig.8 Impact of the probability of getting swappable batteries successfully on the lowest number of batteries each station should hold
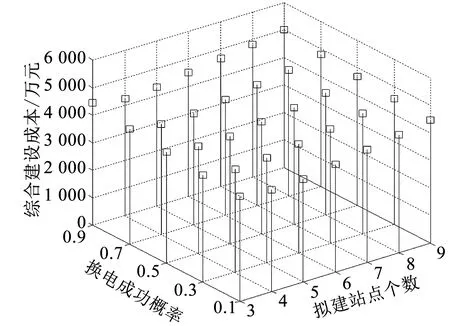
图9 换电成功概率对综合建设成本影响Fig.9 Impact of the probability of getting swappable batteries successfully on the total cost of the recharging system
各站配置的电池数还受电池交换需求影响,建站数较少时,各站需求较高,为满足换电成功概率,所需电池数就较多。以η=0.9为例,在建3个站时,站点2、3需要最少的电池数为55;而建9个站时,需求最大的站点(站5、6)仅需配置37块电池。总体成本受电池组保有成本及站点建设固定成本的影响。表2是η=0.9时的充电设施建设成本。据表2知,建站数越多,站点建设固定成本就越大;而电池采购成本随建站数增加而减少。因此,当c≫K(y)时,总成本会随着站点数减少而减少;而随着站点数不断减少,电池容量增加,K(y)也增加,反而需要增加站点数以减少电池组保有成本,进而减少总成本。因此,规划时需要考虑这两种成本。
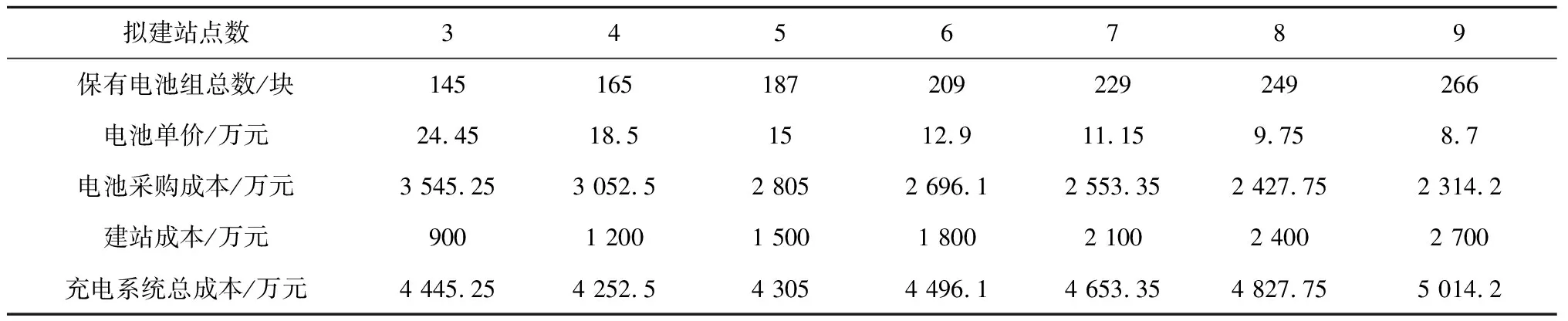
表2 充电设施建设成本Table 2 Construction cost of recharging infrastructure
3.3 充电技术进步的影响
充电技术的进步能缩短充电时间,对换电站系统规划产生重要影响。在η=0.9的情况下,假设μ=1.5、2、2.5 块·h-1三种充电速率。图10为不同充电速率下,各种建站情况的综合成本及保有的总电池数。据图10知,充电速率越高,保有电池数越少,总成本越低。以建4个站为例,μ=1.5、2.5 块·h-1时,系统保有的电池数分别为214、138,总成本分别为5 159万元、3 753万元。
换电成功概率对规划过程至关重要,以建4个站为例分析充电速率对换电成功概率的影响。图11、12分别为不同充电速率下,第3个站点的电池数与无满电电池概率关系及各个站点最少保有电池数。据图11知,同样电池数下,充电速率越高,无满电电池概率越小,即要满足相同的换电成功概率,充电速率越高,各站需保有的电池数就越少。由图12知,在三种充电速率下,站点3应保有的最少电池数分别为48、37、31。
综上所述,充电速率的提高可增加换电成功概率,大大降低保有的最少电池数及建设成本,对电动汽车发展意义重大。

图10 充电技术进步对换电站系统规划的影响Fig.10 The impact of the advance of recharging technology on the battery-swapping station system planning
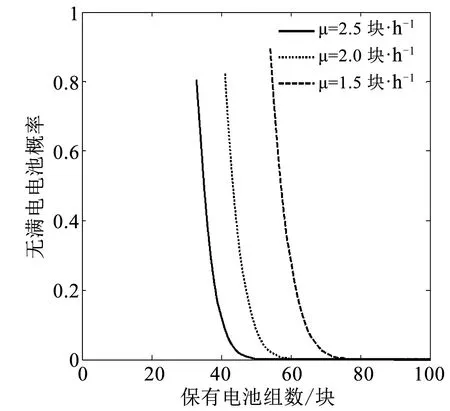
图11 不同充电速率下无满电电池概率与电池数关系Fig.11 Relationship between the number of batteries and the probability of no full batteries under different recharging rate

图12 各站规划保有的最少电池组数Fig.12 The lowest number of batteries that each station must hold
3.4 实例验证
3.1~3.3中的算例是在理想化的交通走廊上的换电站规划,现以现实中京沪高速江苏段为例,验证本文所建模型的实用性。电动汽车电池的特性、价格与电池容量的关系、充电速率等假设与3.1中算例设置中保持一致。根据京沪高速江苏段的具体线路情况、江苏经济发展状况及人民生活水平,对电动汽车的到达率进行分段假设以适应实际情况。京沪高速江苏段全长480.15 km,为方便计算这里取480 km。现研究苏北至苏南侧换电站系统规划。将线路分为三个部分:苏南(160 km)、苏中(140 km)、苏北(180 km)。三个区域的平均需求密度分别取0.3、0.2、0.1次/(km·h),电动汽车往来比例保持不变。仍依据3.1~3.3的算例分析思路,这里不再详细表述,直接给出必要计算结果。各种建站数下的各站点到达率分别为:
(α1,α2)=(30,79);
(α1,…,α3)=(16,35.33,63.33);
(α1,…,α4)=(12,21,35.5,50.5);
(α1,…,α5)=(9.60,18.48,31.44,41.44,41.84 );
(α1,…,α6)=(8,14.67,24.67,31,39.33,35.67 )。
这里仍设η=0.9,根据本文模型,换电站及其保有配置优化结果如图13所示。其中,保有电池成本曲线上标注的数字为该种建站方式下各站保有电池数。在该例中,建设3个站点的系统总成本最低,对应图13中空心圈所标注的位置,各站配备的电池数分别为13、18、41块,总建设成本是2 130万元。
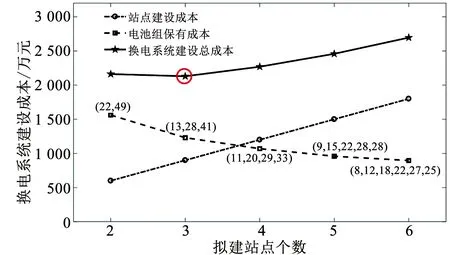
图13 换电系统优化结果Fig.13 The optimal Results of Battery-swapping System
现实中,京沪高速单向平均每50 km设置一处快充站,江苏段有11处快充站,均位于服务区内。若考虑使用换电模式,据本文算例结果建议:苏北至苏南侧的换电站可以利用淮安、泰州、苏州的服务区,建三座换电站,可与快充站合建以减少初期站点建设成本。三处配备的电池数分别为13、28、41块,该结果与现实中江苏的人口及经济发展水平相吻合,苏北地区经济发展相对落后,将来电车普及速度必定不及苏中、苏南地区。实例说明,本文模型对现实中交通走廊的充电基础设施规划有一定的指导意义,具有一定的实用价值。
4 结论
(1)本文考虑了换电站处电池充电及交换的随机运作过程,因此在确定换电站及其电池数量时不仅能够考虑换电需求,还能分析换电成功概率、充电技术进步的影响。
(2)所建模型能综合考虑建站成本和电池采购成本,在满足换电成功概率的约束下,实现建设成本最小的换电站及电池配置。该模型可用于电池交换式电动汽车充电设施规划问题。
(3)依托本文模型,可从以下方面进行拓展:(i) 本文未深入分析充电设施对使用者行为的影响,包括出行行为分析、换装电池的广义费用等,可以此为切入点拓展本文模型,建立多目标规划模型提高对实际需求的适应性。同时,出行行为中的路径选择问题与道路交通网络密切相关,可依托本模型进一步研究交通网络上的换电站及电池规划问题。(ii)要实现服务商成本回收及可持续运营,需要进一步考虑电池交换的有偿使用问题。(iii)未来有必要同时考虑整车充电及电池交换这两种方式对充电站规划的影响。(iv)现实中的补能需求会随时间变化,这对于研究换电站电池调度管理具有重要意义。
