基于有效振动长度的多支撑斜拉索索力识别

危媛丞，李 周，郑荧光

（1.深圳市龙华区大浪街道建设工程事务中心，广东 深圳 518109；2.中建钢构有限公司，广东 深圳 518048；3.湖南大学 土木工程学院，湖南 长沙 410012）

0 引 言

在工程实践中，一般采用千斤顶、压力传感器和埋入式光纤传感器来评估斜拉索的张力，但这些永久设备通常存在成本高昂、制造复杂、耐久性差等缺点［1－3］。基于振动频率法的索力测试技术是目前最为常用的索力测试方法［4－9］，该方法通常采用拾振器测量拉索的自振频率，然后通过预先确定的频率－索力关系式或数值模拟来估计张力。

但在实际工程中，斜拉索由于套筒内橡胶阻尼器的影响，属于多支撑的拉索［11］。对于多支撑拉索，有研究者提出了基于有限元法的索力识别方法［12－16］，但该方法需要建立有限元模型，工程应用不方便。为了更有效地解决多支承斜拉索的索力识别问题，本文提出一种基于振型比与模态频率相结合的索力优化方法。

1 拉索系统与简化

典型斜拉构造如图1所示。斜拉索通常包含3个部分：中间的自由长度部分、两端锚固区、前两部分之间的2个过渡区。锚固区与过渡区通常称为索锚固装置。一般在锚固装置前端设置柔性橡胶约束以减小锚具端部的弯曲应力，缓和疲劳问题。但锚固装置复杂，其细部设计各不相同，在对拉索进行受力分析时，其边界条件很难简化，由于锚固装置对拉索振动的影响仅限于锚固端附近的有限范围，对中间自由长度部分的影响十分有限，因此，本文将多支承的斜拉索等效为具有轴向拉力的简支梁，此简支梁的计算长度为拉索的有效振动长度。

图1 典型斜拉索构造

对于一个受轴向拉力T的简支梁模型，该索力与频率的关系如下。

式中：L为梁的长度；m为拉索线密度；EI为拉索抗弯刚度；fn为第n阶模态的固有频率。

2 等效长度的计算方法

2.1 模态振型比的计算

根据振型叠加原理，梁在任意时刻的振动形状表达式为

式中：qk（t）为第k阶模态位移与时间的函数；φk（xi）为第k阶模态在xi位置的振形幅值。

式（2）在频域内可以写成

式中：Y（xi，ω）、Qk（ω）分别为y（xi，t）和qk（t）的傅里叶转换。

由于拉索系统具有频率易分离和低阻尼的特点，由模态的正交性可得

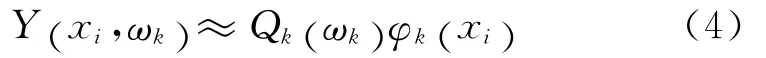
为了确定拉索振型，需要进行多点同步测量，在本次研究中采用FFT识别振动频率，用SSI识别拉索模型的振型。

假设y（x1，t），y（x2，t），…，y（xn，t）是在同一斜拉索的n个不同位置同时测量的n个信号，并且只考虑具有主要贡献的m阶模态。由傅里叶变换可以得到第k阶模态的振型向量

式中：φk（xj）为在xj位置和代表第m 个主要模型的模型顺序的k1，k2，…，km中的与第k个模型相应的振形值，φk（xj）＝φjk。其中，任何一个Y（x1，t），Y（x2，t），…，Y（xn，t）均可以作为式（2）中的公分母Y（xi，t）。通常可以选择振型的峰值作为公分母，从而将模态振型归一化。

2.2 优化目标函数的建立

在本文的研究对象中，由于拉索边界条件的复杂性，正弦函数的坐标原点不再位于梁模型的左端。为了克服描述测量位置的困难，对于对称边界条件，可以将原点定义为两端橡胶约束之间的中点。在这种坐标系下，偶数振型保持正弦函数，但奇数的振形变为余弦函数，两者都在－L／2≤L／2范围之内。换言之，在－L／2≤x≤L／2范围内的理想振型矢量

式中：αk为第k个模型的振幅系数，参数cosin（·）通过式（7）确定。

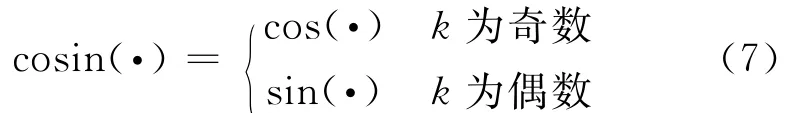
在本文中采用优化的方法来确定拉索的有效振动长度，优化的目标函数定义如下。

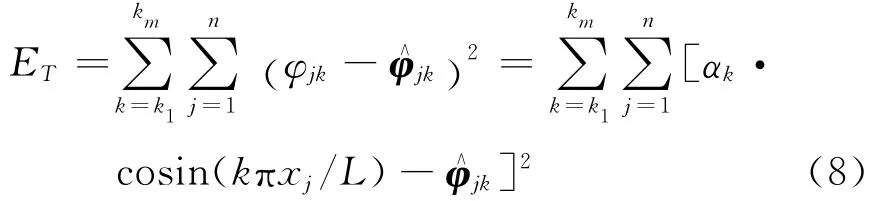
式中有m＋1个未知系数，包括了m个不同的振幅系数αk和L。这是一个非线性优化问题，本文采用MATLAB的优化工具箱进行求解。

2.3 抗弯刚度和索力的识别

得到最优的有效振动长度后，每个振型频率都是张力T和弯曲刚度EI（E为弹性模量，I为截面惯性矩）的简单线性函数，即

随后，根据实测得到的多阶频率，利用最小二乘法可以方便地从辨识出的振动频率中求解出T和EI的最优值。

3 数值验证

以东平水道特大桥为原型进行数值研究。东平水道特大桥为大型斜拉桥，跨径组成为（35＋260＋51.5＋66＋62.5）m，主桥长475.0m。钢主梁采用分离式流线形扁平钢箱梁，混凝土主梁采用分离式预应力混凝土箱形梁。斜拉索采用热挤聚乙烯高强钢丝拉索，采用扇形布置，钢梁侧索距为9.0m，混凝土梁侧索距为6.0m。桥梁布置如图2所示。

图2 东平水道特大桥桥梁布置

本文采用ANSYS软件构建最长索P26和最短索P01的有限元模型，拉索参数如表1所示。考虑减振橡胶的影响，其力学简化模型如图3所示，在2个橡胶位置附近的2个相邻节点上附加一对线性弹簧来模拟橡胶在横向和竖向的弹性约束，对于不同的模型，其弹簧刚度是变化的。为了测试的方便，在实际工程中一般将拾振器布置于拉索接近于桥面的位置。本研究在拉索上布置了5个传感器，选取3阶频率进行分析，对于斜拉索P01和P26，选取的频率阶次分别为1、2、3阶和4、5、8阶。限于篇幅，这里仅列出部分结果，图4为弹簧刚度为1×106N·m－1时P01拉索的1、2阶模态振型，其中，竖向虚线表示减振橡胶位置。由图4可知，多支承拉索的模态振型可以由5个实测得到的模态振型比结合模态振型的正余弦函数得到；橡胶减振片只对其附近区域的振型向量有所影响，在实际工程测试时，可以将拾振器布置远离橡胶片，即以得到较好的实测结果。

表1 拉索计算参数

图3 多支撑拉索有限元模型

根据5个点测试得到的3阶频率和模态即可采用本文方法进行拉索有效振动长度的识别。拉索P01和P26的实测结果分别如表2、3所示。

由表2、3可知：当减振橡胶的弹簧刚度不大于104N·m－1时，可忽略橡胶支撑的影响，拉索的有效振动长度近似于拉索总长减去拉索锚固的长度。当减振橡胶的弹簧刚度不小于108N·m－1时，橡胶可等效成固支竖向支撑，拉索的有效振动长度近似等于拉索两橡胶减振片之间的距离。当减振橡胶的弹簧刚度为104～108N·m－1时，橡胶为弹性支撑，拉索的有效振动长度与弹簧刚度的关系密切。随着弹簧刚度的增加，拉索的有效振动长度逐渐减小。

表2 拉索P01有效振动长度计算结果

图4 拉索P01模态振型对比

表3 拉索P26有效振动长度计算结果

有了拉索的有效振动长度后，即可以将有效振动长度带入公式（8），构建线性方程组，采用最小二乘法识别出拉索的索力和抗弯刚度。表4、5分别为拉索索力和抗弯刚度的识别结果。可以看出：无论是长索P26还是短索P01，拉索的索力识别精度均很高，误差不超过3%，相对而言，长索的精度更高，不超过1%。对拉索抗弯刚度的识别效果不佳，当弹簧刚度为105～106N·m－1时，拉索抗弯刚度的识别误差达到30%以上，这主要是由拉索频率对拉索的抗弯刚度不敏感造成的。当弹簧刚度小于104N·m－1或大于108N·m－1时，拉索的抗弯刚度识别效果相对较好，不超过10%。

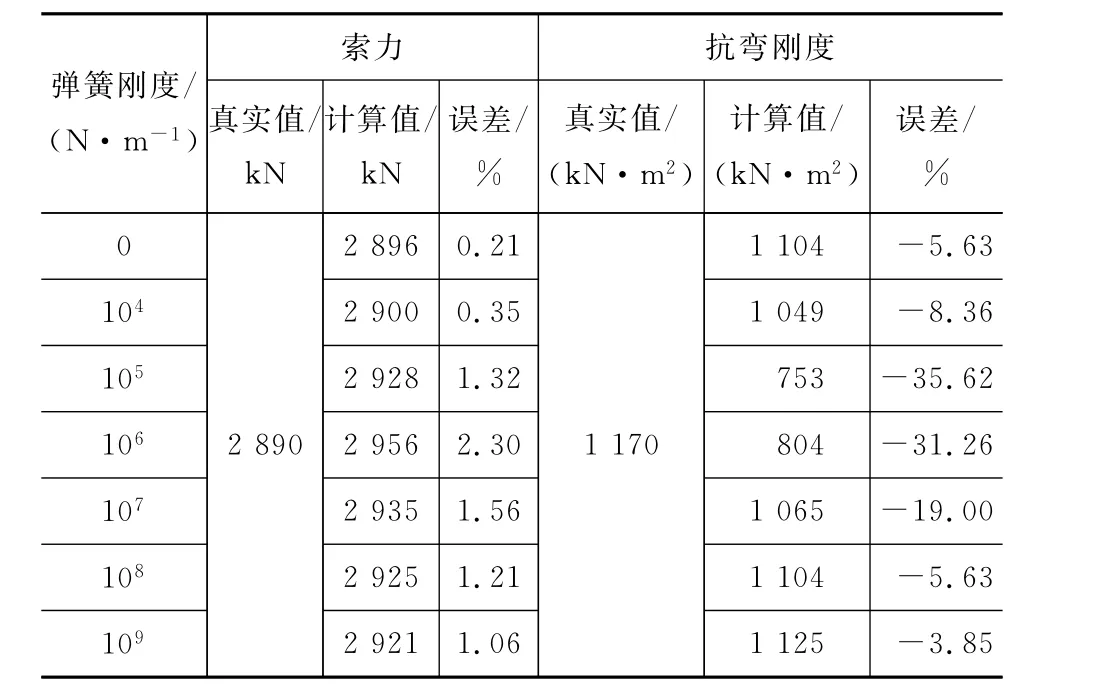
表4 拉索P01的索力和抗弯刚度识别结果

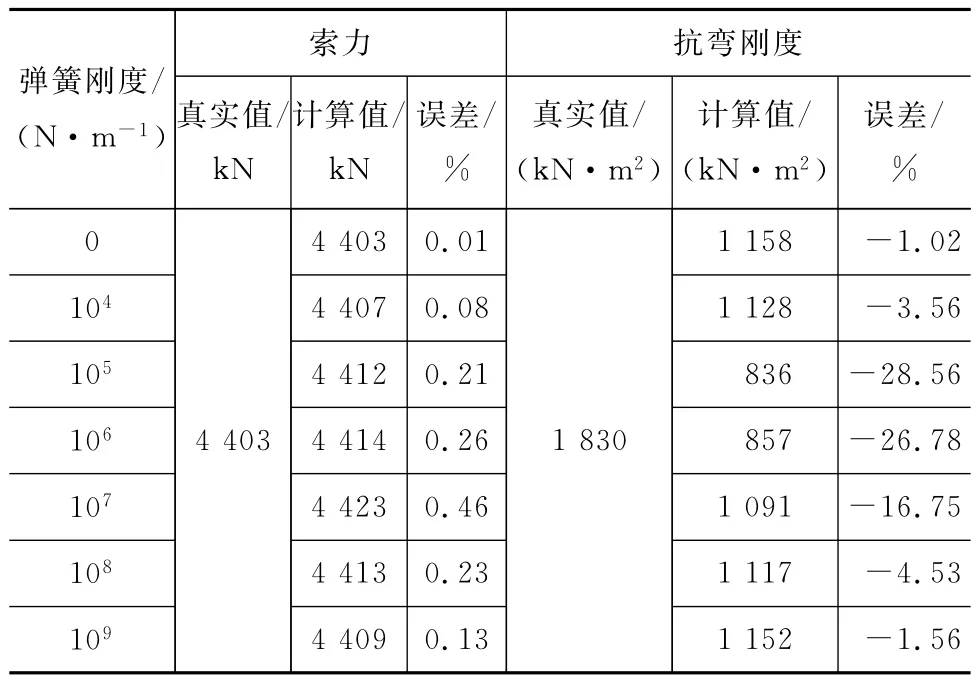
表5 拉索P26的索力和抗弯刚度识别结果

4 工程应用

在东平大桥实际工程中，对其索力进行计算，并与油压表的实测结果进行对比。实测采集的拉索振动信号及FFT分析如图5、6所示，试验得到的拉索索力如表6所示。由表6可知，本文方法的计算值与实测值基本吻合，表明本文方法具有一定的准确度。

表6 索力计算结果对比

5 结 语

本文基于模态振型比与模态频率相结合的概念，提出了一种准确测定斜拉索索力的新方法。该方法通过引入有效振动长度的概念，将复杂边界条件的斜拉索等效为简支欧拉梁，从而采用既有轴拉梁的索力计算公式进行计算。数值计算结果表明，本文提出的斜拉索有效振动长度的计算方法正确可靠。继而根据有效振动长度，由轴拉梁的索力计算公式对拉索的抗弯刚度和索力进行了识别。识别结果表明，本文方法对拉索索力的识别精度很高，短索误差不超过3%，长索误差不超过1%，而抗弯刚度的识别则在一定范围内具有较大误差，这主要是由拉索频率对拉索的抗弯刚度不敏感造成的。最后通过实桥算例，验证了本文方法的正确性。

图5 实测加速度信号

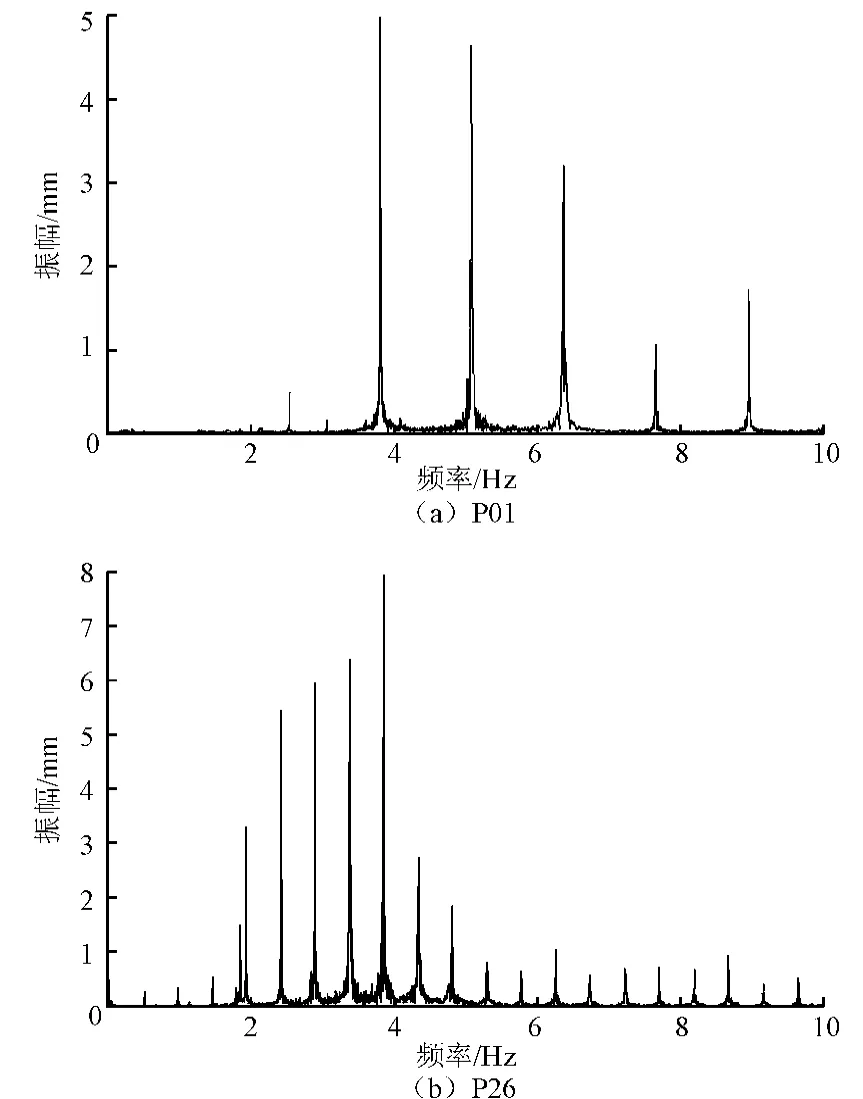
图6 FFT变换后的频谱