侧向局部爆炸荷载下钢质方管的损伤破坏及影响因素研究

余 洋， 纪 冲， 周 游， 龙 源， 谢兴博

(1. 陆军工程大学 野战工程学院， 南京 210007； 2. 西北核技术研究所， 西安 710024)

随着世界范围内恐怖爆炸事件及工业爆炸事故的频繁发生，工程结构抗爆性能的研究日益得到国内外专家学者的关注。金属柱壳(管)具有刚度大、质量轻、易于加工和优异的吸能特性等，广泛应用于化工能源、建筑结构、航空航天等军事或民用领域，其在服役期间可能遭受来自外界爆炸与冲击作用的风险。方管作为柱壳结构的重要形式之一，其在受到爆炸冲击载荷作用时，将产生大塑性变形或发生局部、整体的断裂破坏而导致结构失去原有功能。因此，研究方管结构在爆炸冲击载荷下的动力响应特征，对预测结构的变形特征、提高结构的抗爆能力具有重要的工程应用价值。

目前关于冲击荷载作用下柱壳结构的动力响应研究大多集中在圆柱壳对象[1-5]，而针对方管结构的研究相对较少。Wegener等[6]对简支薄壁方管在片状炸药爆炸荷载作用下的永久变形进行预测分析；Bambach[7]对铝合金方管受到爆炸冲击荷载作用下的局部和整体变形进行试验研究，并根据试验结果得到了计算变形的经验公式；Jama等[8]对三种不同尺寸的方管在线性均布爆炸荷载作用下的动力响应进行了理论和试验研究，并推导了方管整体变形和局部变形过程中的吸能公式。然而针对不同壁厚方管在不同爆源条件局部爆炸载荷作用下破坏效应的研究则极少涉及。

在前述工作的基础上，本文进行三种壁厚Q235钢质方管经受不同强度侧向爆炸荷载的冲击实验，获得方管结构的变形破坏特征及变形参数；利用LS-DYNA动力有限元程序及Lagrangian-Eulerian流固耦合算法，对方管结构在侧向局部爆炸荷载作用的变形过程及破坏形态进行数值计算。通过数值模拟和实验结果的比较分析，获得影响结构变形形态的关键因素及其影响规律，以期为方管结构的抗爆性能分析和变形失效模式预测提供参考依据。

1 实验研究

1.1 实验设置

实验试件为Q235钢质方管，壁厚δ分别为3.0 mm，3.5 mm，4.0 mm，轴向长度L为100 cm，横截面尺寸为100 mm×100 mm。爆炸冲击实验现场布设如图1所示。实验以装药密度为1.61 g/ cm3的裸装圆柱形压装160 g TNT (Trinitrotoluene)药柱(Ф48 mm×54 mm)作为爆炸源，采用电雷管对装药上端面中心进行起爆。实验前平整地面，安装固定好钢支架及钢支座，装药固定于PVC (Polyvinyl Chloride)管上，悬挂于薄壁方管上方并固定在钢支架上，薄壁方管搭接在钢支座上，且确保装药的轴线垂直于方管的迎爆面。

图1 实验设置示意图

实验主要通过调整装药比例距离Z以及方管结构宽厚比W，以获得不同初始条件下方管结构的变形形态及变形参数值，Z与W定义如式(1)和式(2)所示。

(1)

式中：R为装药下表面至管壁迎爆面的距离；h/2为装药中心至装药下表面距离；C为炸药质量。

(2)

式中：B为方管截面宽度；δ为方管壁厚。

实验后方管结构各变形参数如图2所示。其中：r1为方管结构凹陷变形区径向宽度；r2为方管结构凹陷变形区轴向长度；d为方管结构迎爆面中心点挠度。

(a) 俯视图(b) 侧视图

图2 变形参数说明

Fig.2 Sketches of deformation paramenters

1.2 实验结果分析

爆炸载荷作用下方管结构的冲击变形参数及宏观形态如表1和表2所示。由实验结果和数据可以看出，在本实验条件下, 比例距离以及方管结构宽厚比的改变对薄壁方管凹陷变形相关参数d，r1，r2影响较大。

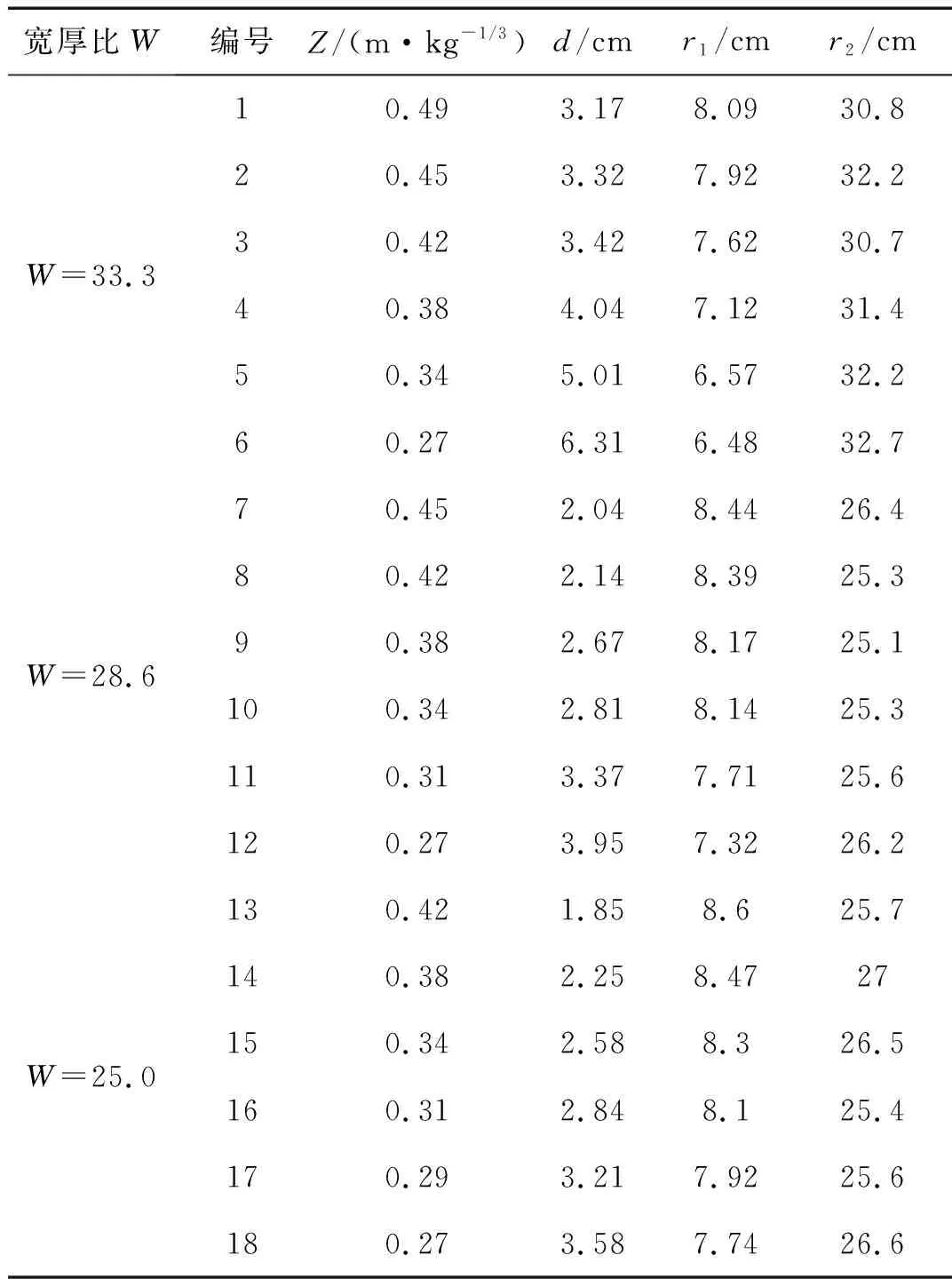
表1 薄壁方管受爆炸荷载的冲击变形参数

1.2.1 装药比例距离对方管结构破坏及动态响应的影响

为研究比例距离Z对方管结构破坏及动态响应的影响特性，以宽厚比W=33.3方管为例进行分析。图3为实验测得迎爆面轴向中心线各点最大挠度随装药距离变化曲线图。

从图3可以看出，在迎爆面轴向中心点处挠度最大，沿着轴向中心线向方管两侧挠度变化逐渐减小；且在不同的装药比例距离下方管结构挠度差异在轴向中心点处最大，沿着轴向中心线向方管两侧挠度差异逐渐减小。同时可以看出方管结构中心线上的挠度变化，在离轴向中心点约175 mm处趋于稳定不再减小，且不同比例距离下方管结构挠度的变化差异也趋于一较小稳定值。

图3 不同装药比例距离下薄壁方管轴向各点最大挠度变化曲线

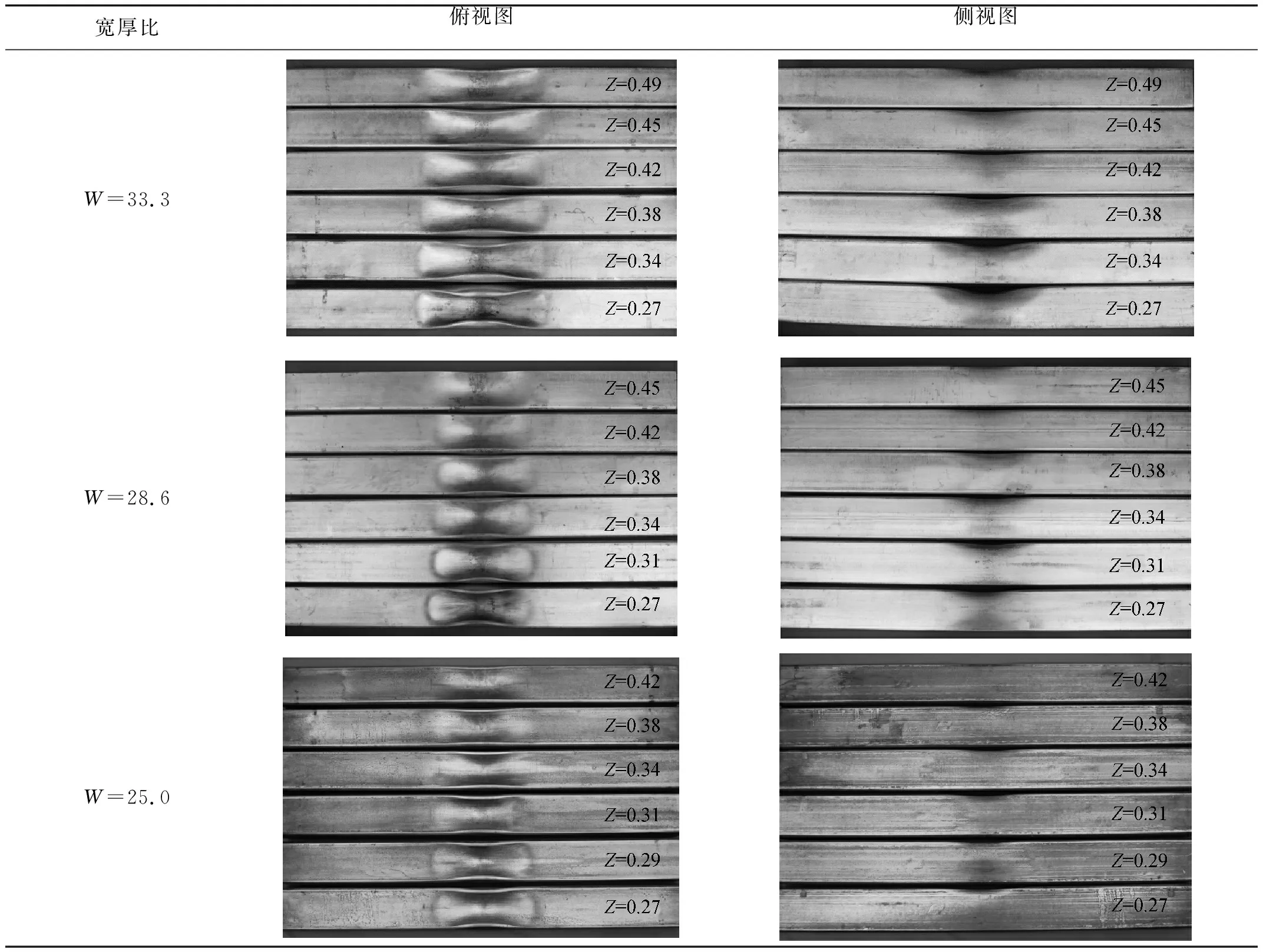
宽厚比俯视图侧视图W=33.3W=28.6W=25.0

为定量研究装药比例距离Z对方管迎爆面中心点挠度d的影响规律，引入中心点最大挠度随比例距离变化的增益系数a。其中，增益系数a定义为

(3)

式中：比例距离Z1分别为0.49，0.45，0.42，0.38，0.34 m/kg1/3，对应比例距离Z2分别为0.45，0.42，0.38，0.34，0.27 m/kg1/3；d1为比例距离分别为0.49，0.45，0.42，0.38，0.34 m/kg1/3时中心点最大挠度，对应的d2是比例距离分别为0.45，0.42，0.38，0.34，0.27 m/kg1/3时中心点最大挠度。按照本文的定义及表1中的实验数据，装药比例距离在0.27～0.49 m/kg1/3具体计算结果对比情况如图4所示。

如图4所示，在比例距离W由0.49减小至0.42时，中心点处挠度的增长速率较稳定(比例距离从0.49减小至0.45和0.42时，a分别为3.75和3.33)；而在比例距离由0.42减小至0.27时，中心点挠度的增长速率加剧(比例距离从0.42减小至0.38，0.34和0.27时，a分别为15.5，24.25和18.57)。可见比例距离越小，爆炸载荷对方管结构的损伤越大，且挠度变化呈加速增长趋势。分析原因之一为，在一定范围内方管结构距爆心距离的增加，爆炸产物作用于方管结构上的压力并不是呈线性下降，而是呈指数下降(即装药比例距离由0.49～0.42阶段减小至0.42～0.27阶段时，挠度变化急剧增大)；另外在距爆心较近距离内，方管结构迎爆面承受的冲击荷载主要是爆炸产物和空气冲击波的共同作用。而在较大的装药比例距离时，爆炸荷载主要是由于空气冲击波的单独作用。

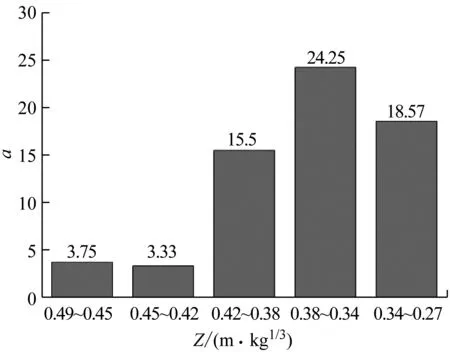
图4 中心点最大挠度随装药比例距离变化

表3给出宽厚比W=33.3时方管实验截面图。实验表明随着比例距离的减小，方管结构径向两侧直角边向迎爆中心点位置移动的程度逐渐增大。

设方管边角向迎爆面中心点移动增量随装药比例距离变化的增益系数为b，则

(4)

式中：比例距离Z1分别为0.49，0.45，0.42，0.38，0.34 m/kg1/3，其对应比例距离Z2分别为0.45，0.42，0.38，0.34，0.27 m/kg1/3；r1α是比例距离分别为0.49，0.45，0.42，0.38，0.34 m/kg1/3时方管结构凹陷变形区径向宽度，对应的r1β是比例距离分别为0.45，0.42，0.38，0.34，0.27 m/kg1/3时方管结构凹陷变形区径向宽度。

表3 薄壁方管中截面变形图(W=33.3)

按照本文的定义及表1中的实验数据进行计算，装药比例距离由0.49减小至0.34时，方管结构径向两侧直角边向中心迎爆点位置移动变化越来越快(装药比例距离由0.49分别减小至0.45，0.42，0.38，0.34 m/kg1/3时，增益系数b分别为4.25，10，12.5，13.57)；比例距离由0.34减小至0.27时，方管结构径向两侧直角边向中心迎爆点位置移动继续增加，但这种增加变化显著减小(增益系数b为1.29)，如图5所示。分析原因，装药比例距离在由0.49减小至0.34时，r1的增益系数b增大原因与挠度d的增益系数a增大原因相似；在装药比例距离由0.34减小至0.27时，r1的增益系数b减小是因为爆炸载荷作用于方管结构的能量，一部分开始转化为使方管两侧壁面径向宽度的增大，从表3可以看出Z=0.27 m/kg1/3方管两侧壁面宽度显著加宽。

图5 方管两侧直角边移动随装药比例距离变化

1.2.2 宽厚比W对方管结构破坏及动态响应的影响

为分析方管结构不同宽厚比受爆炸载荷作用的破坏及动态响应特性，以Z=0.27 m/kg1/3时方管结构为例分析，表4为方管结构中截面变形实验图。可以看出宽厚比增大时，方管中心点挠度变化明显增大。设挠度随宽厚比变化的增益系数为c，则

(5)

式中：d3.0，d3.5，d4.0分别是宽厚比为33.3，28.6，25.0时中心点处最大挠度。

按照本文的定义及表1中的实验数据进行计算，在装药比例距离同在Z=0.27 m/kg1/3的爆炸载荷作用下，当宽厚比W由28.6增大至33.3和由25增大至28.6时，中心点最大挠度d的变化增大6.4倍(即c=6.4)。由此可见，宽厚比的改变对方管结构在爆炸载荷的作用下挠度变化影响较为突出。

表4 薄壁方管中截面变形图(Z=0.27 m/kg1/3)

此外由表4还可以看出，宽厚比W增大时，方管结构凹陷变形区径向宽度r1显著减小。设凹陷变形区径向宽度r1随宽厚比W变化的增益系数为f，则

(6)

式中：r3.0，r3.5，r4.0是宽厚比分别为33.3，28.6，25时凹陷区的径向宽度。

在装药比例距离同为Z=0.27 m/kg1/3的爆炸载荷作用下，当宽厚比W由28.6增大至33.3和由25增大至28.6时，凹陷区的径向宽度r1的变化增大5.5倍(即f=5.5)。由此可见，宽厚比的改变对方管结构在爆炸载荷的作用下凹陷区的径向宽度变化影响较为突出。

1.2.3 方管结构凹陷变形模式分析

将方管的凹陷变形分为两种模式，如图6所示。模式1下，爆炸载荷主要使方管的轴向变形，使凹陷朝轴向扩展(如W=33.3，Z=0.49，0.45 m/kg1/3；W=28.6，Z=0.45，0.42 m/kg1/3；W=25，Z=0.42，0.38，0.34 m/kg1/3)。模式2下，爆炸载荷主要使方管的径向变形，此时凹陷轮廓较为明显(如W=33.3，Z=0.42，0.38，0.34，0.27 m/kg1/3；W=28.6，Z=0.38，0.34，0.31，0.27 m/kg1/3；W=25，Z=0.31，0.29，0.27m/kg1/3)。

(a) 模式1(b) 模式2

图6 薄壁方管凹陷变形模式

Fig.6 Deformation model of thin-walled square tube dent

从表2可以看出，宽厚比分别为W=33.3，W=28.6，W=25时，在模式1下随着装药比例距离的增大，方管结构凹陷变形轴向宽度r2逐渐增大；同样在模式2下，随着装药比例距离的增大，方管结构凹陷变形轴向宽度也逐渐增大；而由模式1变化到模式2时，尽管装药比例距离增大，但方管结构凹陷变形轴向宽度出现减小。

分析原因，当装药比例距离增大时，爆炸载荷作用于薄壁方管上的能量，首先使其凹陷变形沿轴向扩展，形成模式1；当装药比例距离增大为一定值时，凹陷变形由模式1转化为模式2，爆炸载荷作用于方管结构上的能量更多的转化为使两侧直角边向迎爆中心点位置移动(即方管结构凹陷区的径向变形)，此时，中心点的挠度变化和两侧直角边向迎爆中心点位置移动开始加剧变化；比例距离继续增大时，凹陷变形呈模式2变化，爆炸载荷作用于薄壁方管上的能量，使其中心点的挠度、轴向凹陷变形长度、两侧直角边向迎爆中心点位置移动变化继续增大。此外由于宽厚比的差异，宽厚比W=33.3的方管，在Z=0.45 m/kg1/3时凹陷变形由模式1开始变化为模式2；宽厚比W=28.6的方管，在Z=0.42 m/kg1/3时凹陷变形由模式1开始变化为模式2；宽厚比W=25的方管，在Z=0.34 m/kg1/3时凹陷变形由模式1开始变化为模式2。可见试件宽厚比越小，凹陷变形由模式1开始变化为模式2所需更小的装药比例距离。

2 数值计算分析

为深入研究方管结构在爆炸荷载作用下的动力响应过程及失效特性，重点对宽厚比因素影响进行分析。选取Z=0.27 m/kg1/3时，壁厚分别为W=33.3，W=28.6，W=25的三种工况，采用LS-DYNA有限元程序对方管结构受侧向爆炸荷载作用过程进行数值模拟研究。

2.1 数值计算模型

根据本文所研究对象的特性，采用多物质ALE算法，即将气体爆轰产物、空气等与薄壁方管等固体结构的相互作用进行耦合计算。在实际建模过程中，定义炸药、空气为Euler网格，定义方管结构为Lagrange网格。由于实验时圆柱壳轻搭于支架上且与支架接触面较小，圆柱壳变形时受支架的影响近似可以忽略。故在不影响计算精度情况下为提高计算速度，将圆柱壳两端边界设置为自由状况。鉴于上述物理模型的对称性，可取原型的1/4建立计算模型，如图7所示。其中将对称面上的节点设置为对称约束，并将空气侧面定义为透射边界。采用SOLID164六面实体单元划分网格，空气域和炸药的网格划分为0.2 cm，方管中心区域一侧15 cm内网格划分为0.1 cm，剩余部分网格划分为0.2 cm，方管四个边角处采取4等分划分。并采用cm-g-μs单位制。

2.2 材料模型及参数

TNT装药采用高能炸药模型，其爆轰产物的膨胀采用Jones-Wilkins-Lee(JWL)状态方程[9]进行描述，并假定爆轰前沿以常速率传播；空气采用空白材料模型，状态方程采用理想气体状态为p=(γ-1)ρe0/ρ0。其中空气初始密度ρ0=1.29×10-3g/cm3，绝热指数γ=1.4，气体比内能e0=0.25 MPa；Q235钢材料动态本构关系采用考虑应变率效应的Johnson-Cook材料模型[10]进行描述，其具体参数见文献[11-12]。

图7 有限元计算模型

2.3 数值计算结果及分析

表5所示为Z=0.27 m/kg1/3时不同宽厚比下方管结构屈曲变形效应的数值计算结果与实验现象的对比，可以看出两者具有良好的一致性，说明本文建立的计算模型和选取的材料参数合理，数值计算结果可信。

为研究薄壁方管表面不同位置处凹陷变形以及应变分布规律，选取薄壁方管迎爆面上若干关键点进行分析。其中节点A为方管迎爆面中心点位置，节点B、节点C分别位于距离节点A2.5 cm和5 cm处，节点具体位置如图8所示。

图9(a)和图(b)分别给出了W=33.3、Z=0.22 m/kg1/3时方管径向A，B，C处挠度-时间曲线，以及Z=0.27 m/kg1/3、W分别为33.3，28.6，25.0时A点处挠度-时间曲线。可以看出，从A点～B点和从B点～C点的33.3，W=28.6的试件在500 μs后A点挠度基本不再变化，而W=25.0的试件在1 500 μs后A点挠度才逐渐趋于稳定。

表5 方管变形数值模拟与实验对比

图8 节点选取示意图(单位：cm)

(a) W=33.3，Z=0.22 m/kg1/3

(b) Z=0.27 m/kg1/3, W=33.3，W=28.6，W= 25.0

为配合相关分析，定义方管结构不同部位的变形形态如图10所示。图11所示为Z=0.27 m/kg1/3时宽厚比分别为W=33.3，W=28.6，W=25.0的方管结构不同节点应变-时间曲线。

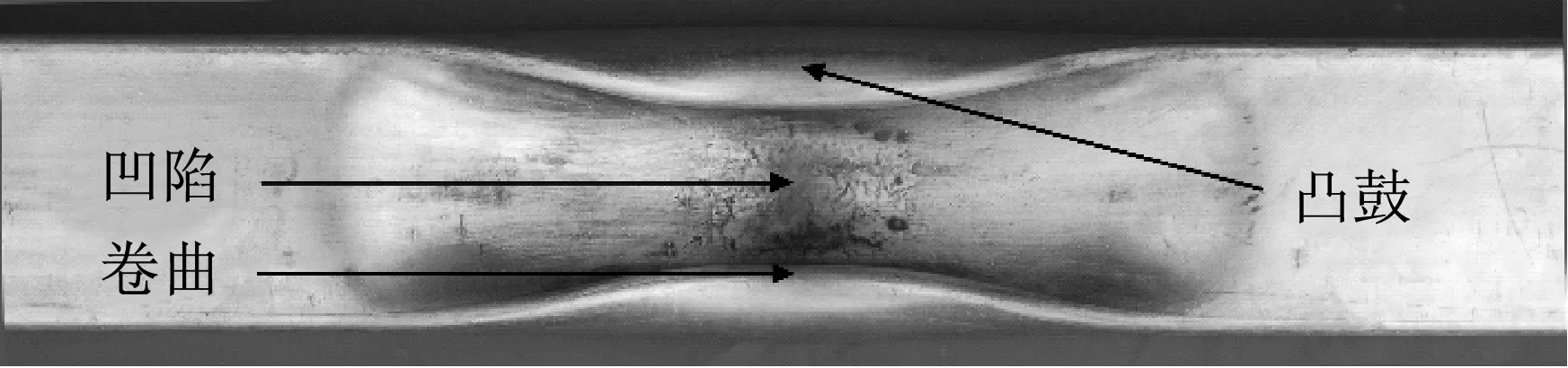
图10 方管不同部位变形形态

(a) W=33.3

(b) W=28.6

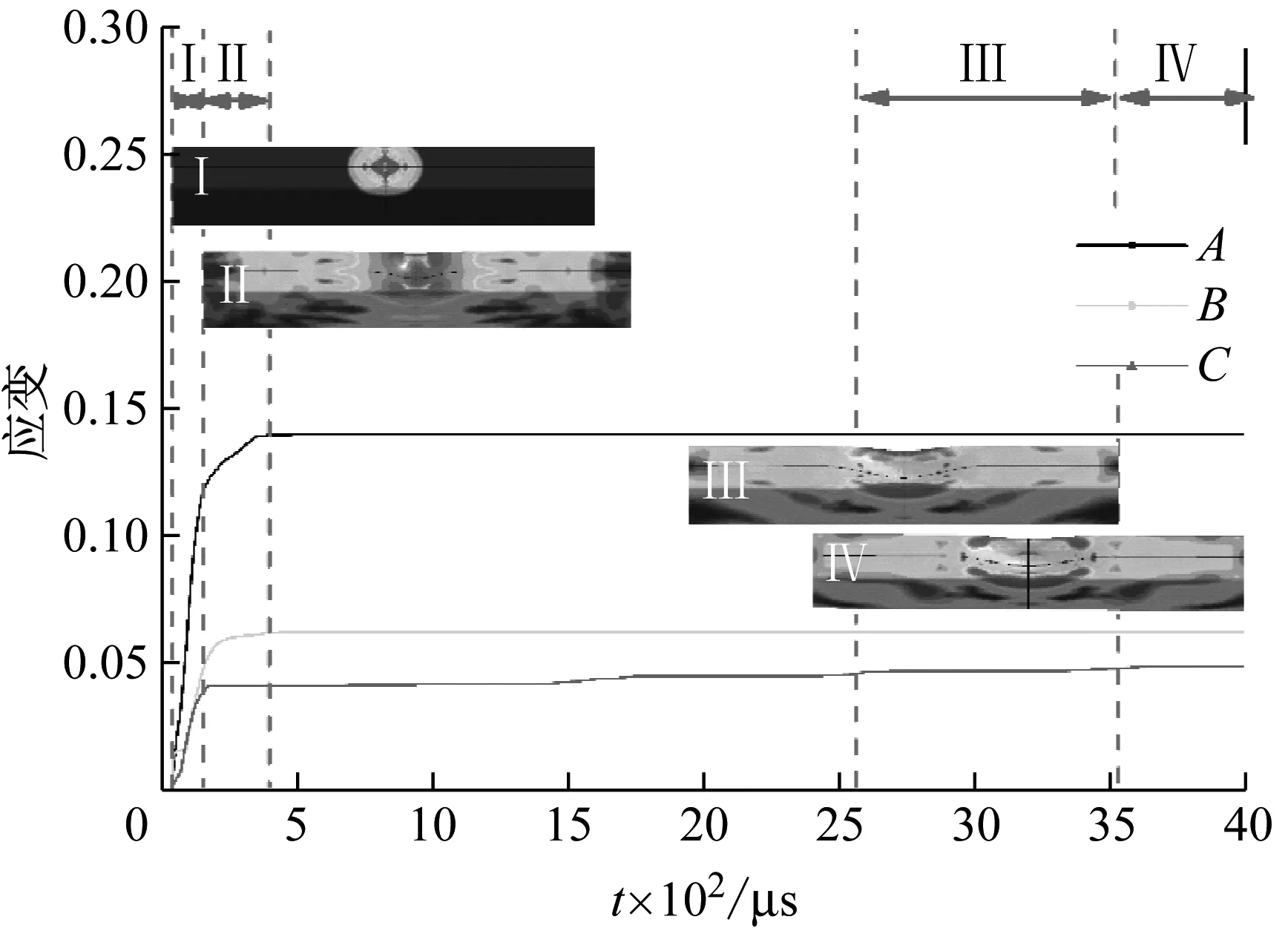
(c) W=25.0

将方管变形过程分为四个阶段：在阶段I，方管迎爆面中心区域发生线弹性凹陷变形；在阶段 II，方管迎爆面中心区域发生塑性变形；在阶段III，方管迎爆面中心区域继续发生塑性变形同时，方管结构两侧边角发生卷曲变形；在阶段IV，方管结构两侧边角继续发生卷曲变形且两侧壁面出现凸鼓变形。图11中所示的I、II两个阶段为针对节点A应变时程曲线进行划分，III、IV两个阶段为针对节点C应变时程曲线进行划分。在阶段I ，A点应变随时间变化不断增加且呈线性关系即材料发生线性弹性变形。随后进入阶段II，A点应变随时间变化继续增大，结构开始发生塑性变形。在阶段III，已经发生塑性变形的C点，其应变随时间变化稍有增大，方管结构两侧边角开始发生卷曲折叠变形。在区域IV，C点应变随时间变化逐渐趋于稳定值，方管结构两侧边角弯曲折叠变形加剧且方管侧壁面最终形成凸鼓变形。

从图11中可以看出，宽厚比为W=33.3时，装药在结构中心正上方起爆后的550 μs内，爆炸载荷作用于方管的能量主要用于材料的塑性屈曲变形。而宽厚比分别为W=28.6，W=25.0时塑性屈曲变形在前400 μs已经完成，可以看出宽厚比越大发生塑性屈曲变形的时间越长。装药在结构中心正上方起爆后的700 μs，2 000 μs，2 550 μs，宽厚比分别为W=33.3，W=28.6，W=25.0的薄壁方管两侧边角开始发生卷曲变形，可以看出随着宽厚比的减小，方管两侧边角开始发生卷曲所用时间越长。装药在结构中心正上方起爆后的1 500 μs，3 000 μs，3 530 μs，宽厚比分别为W=33.3，W=28.6，W=25.0的薄壁方管两侧边角开始发生卷曲变形和侧面凸鼓变形，可见宽厚比分别为W=28.6，W=25.0的方管结构进入IV区之前所经历的时间较长，然而此两类试件在IV区作用下经历时间较短，因此宽厚比分别为W=28.6，W=25.0的方管结构侧面发生凸鼓变形程度较小，这与表1中的实验现象相吻合。

3 结 论

(1) 薄壁方管在160 g压装TNT装药产生的爆炸场中的冲击实验表明，由于装药比例距离Z以及方管结构宽厚比W的不同，薄壁方管呈现出不同的变形模态。且由于方管两侧直角边的吸能作用，增加了方管结构的抗损伤能力。

(2) 当方管宽厚比一定时，由于随距爆心距离的增大爆炸作用产生的压力呈指数衰减，以及爆炸近区范围内结构受爆炸产物和空气冲击波的共同作用，较远范围内主要是空气冲击波的作用，导致随装药比例距离的减小(即目标物朝爆心移动)，方管结构迎爆面中心点挠度及径向两侧直角边向中心迎爆点位置移动变化越来越快。此外由于方管两侧壁面径向宽度增大的吸能作用，随装药比例距离减小至一定值时，径向两侧直角边向中心迎爆点位置移动变化出现减小。

(3) 当装药装药比例距离一定时，随着方管结构宽厚比的增大，方管迎爆面中心点挠度及径向两侧直角边向中心迎爆点位置移动变化显著增大。可见，方管结构宽厚比的变化对方管变形形态影响较大，在进行结构设计和工程防护计算时应重点关注。

(4) 本文采用的数值模拟方法得到结构变形形态以及不同节点处应变-时间曲线。结合实验结果将不同节点处方管结构变形分为四个阶段，分析了不同时刻下方管迎爆面中心点和中截面直角边处变形经历的不同阶段。研究结论为薄壁方管结构的抗爆及安全性评估提供分析依据。