FA-PMA-VMD方法及其在齿根裂纹故障诊断中的应用

2018-08-27程军圣李梦君欧龙辉

振动与冲击 2018年15期

程军圣, 李梦君, 欧龙辉, 杨宇

(湖南大学汽车车身先进设计制造国家重点实验室，长沙 410082)

齿轮作为旋转机械中不可或缺的一部分，其故障信号往往表现出非线性非平稳特性，针对这种非线性非平稳特性，常采用时频分析方法对这类信号进行预处理。常用的时频分析方法有经验模态分解(Empirical Mode Decomposition, EMD)等方法[1-3]。但是EMD方法是基于“经验性”算法，缺少坚实的数学基础[4]，并且存在模态混淆等缺陷[5]。Dragomiretskiy等[6]最近提出了一种新的分解方法—变分模态分解(Variational Mode Decomposition，VMD)。它是一种具有坚实的数学基础的分解方法，通过建立对应的约束变分模型表达式，引入二次惩罚因子和拉格朗日乘法算子，将约束性变分问题变为非约束性变分问题，最终获得具有数学意义并且能有效抑制模态混叠现象的带限内禀模态函数。

VMD相比EMD等方法，在很多方面表现出更加优异的性能[5-9]。Zheng等将VMD方法应用在碰撞信号的去噪上，效果明显优于EMD方法，文献[7]论证了VMD方法有很好的滤波特性，文献[8]等将VMD方法应用到旋转机械的碰摩故障诊断，唐贵基等将VMD方法应用到轴承的早期故障诊断。但是VMD方法自身也存在着一些缺陷。首先，在用VMD方法分解信号之前，必须预先设定模态数和惩罚参数，文献[7]将去趋势波动分析(Detrended Fluctuation Analysis，DFA)方法与VMD方法相结合，建立光纤陀螺信号的长相关系数α0与模态数k的关系式，以计算α0获得最佳的模态数，但是忽略了惩罚参数α对对于VMD分解效果的影响，且仅应用于光纤陀螺信号。文献[8]虽然考虑了惩罚参数α对于VMD分解效果的影响，但是只能将VMD算法运用到简单的谐波信号和噪声的合成信号。其次，在用VMD方法对信号分解后，进行滤波或提取特征值等不同处理时，需要选择合适的分量和排序，但是VMD方法存在分解出来的分量排列不规律的缺陷，从而给分量的选择和排序带来困难。

针对上述缺陷，本文首先把主模态分析(Principle Mode Analysis,PMA)与VMD方法结合，使带限内禀模态函数(Band-Limited Intrinsic Mode Function, BIMF)分量按照一定的规则排序。然后用萤火虫算法对变分模态分解方法的最佳影响参数[k,α]组合进行搜索，并提出一个新的特征值—正交低峰值作为萤火虫算法优化[k,α]的目标。搜索得到的最佳结果设定变分模态分解算法的惩罚参数α和分量个数k，并根据PMA处理预先设定的故障特征参数综合特征将BIMF分量进行排序。最后，用复杂调幅调频仿真信号对FA-PMA-VMD方法进行仿真分析，并将FA-PMA-VMD方法运用到实际齿根裂纹故障诊断中，验证改进VMD方法的实际有效性。

1 FA-PMA-VMD方法

1.1 PMA-VMD方法

式(1)信号其时域波形如图1所示，由中心频率分别为200 Hz,400 Hz,20 Hz三个分量合成。

(1)

图1 输入信号的时域波形图

直接用VMD分解后各个BIMF分量及其频谱图，如图2和图3所示，可观察到，这些BIMF分量并没有按照中心频率高低的顺序这类的规律排列。

当实际信号的BIMF分量较多，对于多个排列无规律的BIMF分量，需要重点研究信号的一个或多个特征时，无法直接判断哪一个BIMF分量的综合特征最明显，也无法直接判断中心频率大小相邻的几个BIMF分量之间的关系。因此需要一种针对特征参数分析的方法对VMD方法分解的BIMF进行分析处理。本文引入PMA方法对VMD方法分解的分量进行排序。PMA是受主分量分析启发，根据故障特征参数，把主模态用于振动信号BIMF分量分析的方法。

本文把某种故障特征最明显的BIMF分量称为主模态分量，主模态分量对应的模态称为主模态。PMA方法为：

步骤1故障信号X(t)经过信号分解后为个n个BIMF与余量res之和即

(2)

步骤2提取第k个BIMF的n种故障特征参数MK1,MK2,MK3,…,MKn,将这些故障参数组成一个故障特征参数向量FK=[MK1,MK2,MK3,…,MKn](k=1,…,n)。FK可以组成一个故障特征参数矩阵F

F=(F1,F2,F3,…,FN)T

(3)

m=(1,2,…,n)

(4)

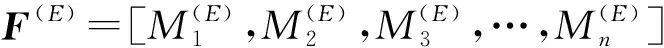
m=(1,2,…,n)

(5)

步骤5式(5)可以看到协方差矩阵L为方阵，求解L的特征值λ与特征向量v

Lv=λv

(6)

步骤6将特征值按大小排列λ1≥λ2≥…≥λn,每个特征值λk的单位化的特征向量组成的空间V

V=(v1,v2,…,vn)T

(7)

步骤7F(E)到空间V的投影表示为S(S=(s1,s2,…,sn)T)。

(8)

步骤8计算各sk对应的故障特征参数列的投影和Bk

(9)

步骤9按照投影绝对和Bk的大小顺序，把Bk对应的BIMF分量进行排序，得到对一个信号的BIMF分量进行主分量分析的结果。

含(E)表示单位化后的变量，故障特征参数矩阵通过步骤3～步骤6的变换，消除了各个特征参数向量的相关性，并得到了一组故障特征参数矩阵的单位正交基，保证在步骤7中的单位化故障特征参数投影信息独立性，步骤8以投影和的方式评判综合信息量的大小。第k个BIMF分量对应的特征参数向量在空间V中的投影和sk越大，说明该BIMF所包含的综合故障信息量越大，其对应的模态对故障越敏感。

PMA-VMD方法是通过VMD将输入信号分解后，把PMA用于对BIMF的分析的方法。具体步骤如下：首先通过VMD方法对信号进行分解，得到BIMF分量；其次提取各BIMF分量的故障特征参数，得到故障特征参数向量；然后用PMA对故障特征参数进行分析，得到综合故障特征的大小顺序；最后按照故障特征的大小顺序对BIMF重新排序。

通过上面分析可以发现，PMA-VMD方法对故障特征参数综合排序，以达到分解出的BIMF分量按照所选的故障特征参数综合特征从强到弱排列。

本文此处以频率重心为特征参数，模态的个数k依据仿真信号的情况设置为3，惩罚参数α设置为1 200。

利用PMA-VMD对于式(1)对应的输入信号分解后的结果如图4所示。对比图4与图2，图3，可以发现用PMA-VMD对输入信号进行分解后BIMF分量按照中心频率的大小，从小到大排列。

图2 各个分量的时域波形图

Fig.2 The time domain waveform of each BIMF signal

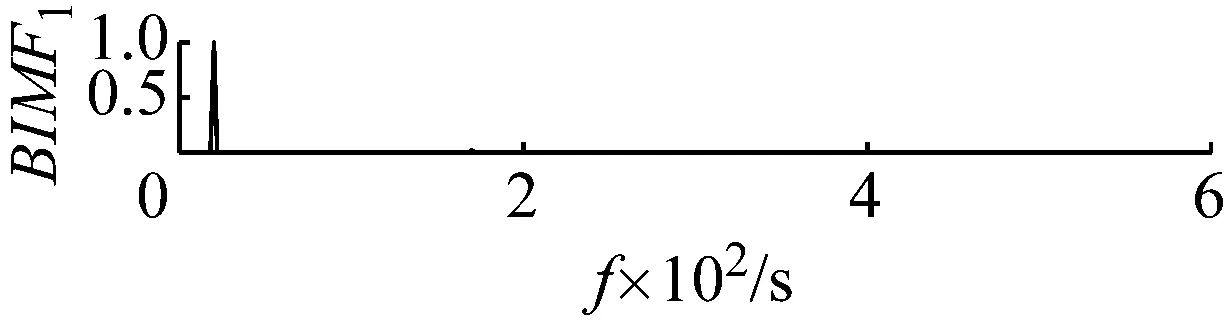
图3 各个分量的频谱

Fig.3 The frequency spectrum of each BIMF signal

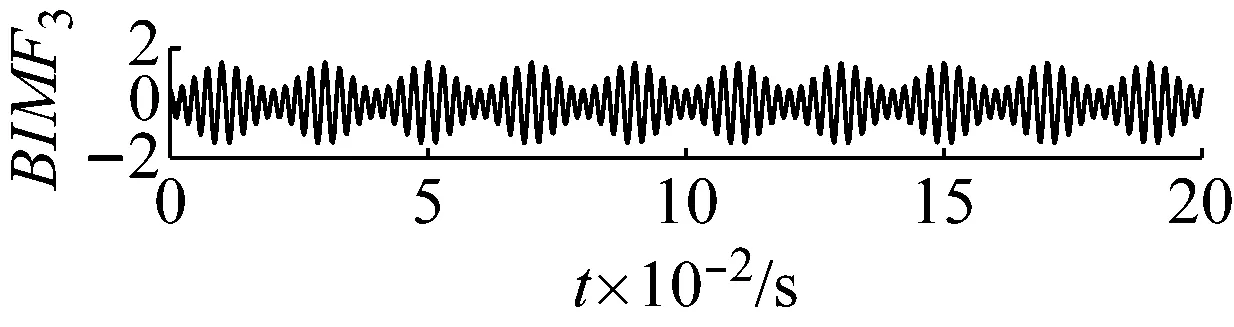
图4 各个分量的时域波形图

Fig.4 The time domain waveform of each BIMF signal

1.2 FA-PMA-VMD方法

VMD在对信号分解前，要给出模态的个数，和惩罚参数，即人为设定k的值和α值。根据上文可以知道，模态个数选取的多少会直接影响最终的分离结果。

本文以式(1)为输入信号，来试验不同[k,α]参数的选取对于VMD算法的分解效果的影响。

当k值取4，同时取一个极大的惩罚参数值α=3×106。此时中心频率为200 Hz的调幅调频信号完全被舍弃,如图5和图6所示。

当k值取4，同时取一个较小的惩罚参数值α=300，此时三个中心频率为20 Hz,200 Hz和400 Hz都存在三个BIMF分量中，但是中心频率为200 Hz的调幅调频信号被分到了BIMF2,BIMF3两分量中，如图7和图8所示。

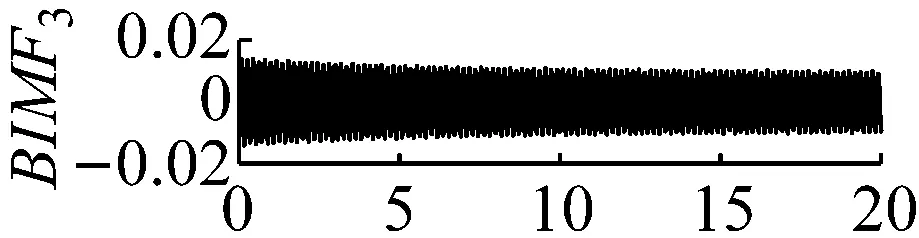
图5k=4,α=3×106时域波形图

Fig.5 The time domain waveform of each BIMF signalk=4,α=3×106

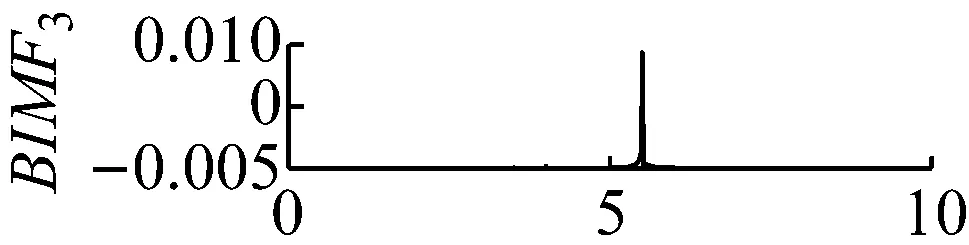
图6 k=4,α=3×106频谱

Fig.6 The frequency spectra of each BIMF signalk=4,α=3×106

图7k=4,α=300时域波形图

Fig.7 The time domain waveform of each BIMF signalk=4,α=300

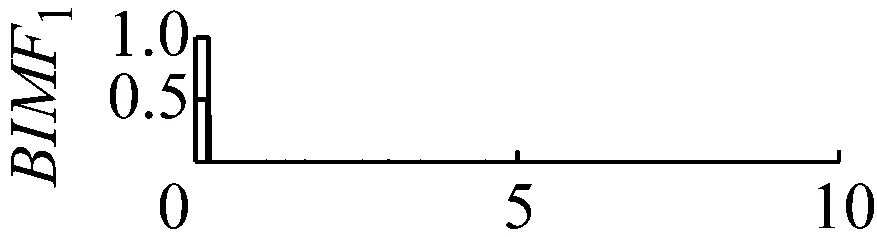
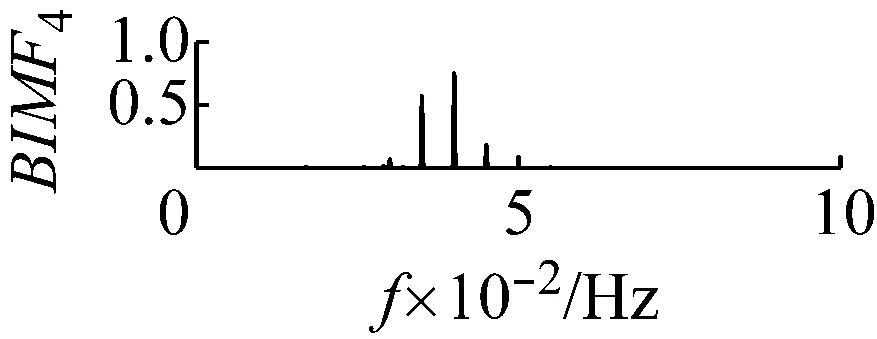
图8 k=4，α=300频谱

Fig.8 The frequency spectra of each BIMF signalk=4，α=300

由于k值和α的选取对于故障的提取至关重要。而对一个参数单独优化往往会忽略这两个参数之间的相互影响，只能获得相对最优的结果。因此，本文引入萤火虫算法对两个影响参数同时进行优化，以避免人为主观因素的干预，自动筛选出最佳的影响参数组合。

利用萤火虫算法搜寻VMD算法的模态数和惩罚参数α时，需要一个评价参数来评价萤火虫每次更新位置的适应度。本文引入正交低峰值作为优化目标，正交低峰值是一个新的评价参数，其计算如式(10)所示，式(10)中k为分量的个数，m为萤火虫的个数。

正交低峰值的计算条件是BIMFi,BIMFi+1为中心频率相邻的两个BIMF分量。

(10)

I=Zm=F(k,α)

(11)

β(r)=β0e-γrm

(12)

式中:k为分量的个数，α为惩罚参数，这两个参数作为函数的输入变量，分别为萤火虫算法中的x轴和y轴上的变量;I为函数的输出变量，为萤火虫算法中z轴的变量。其计算原理如图9所示。

图9 目标函数计算原理图

式(10)和式(11)对目标函数的定义可知，在用萤火虫算法搜寻VMD算法的模态数k和惩罚参数α时，首先需要以频率重心为特征参数，通过PMA对BIMF分量按照中心频率的大小，从小到大排列，以便求出对应分量的个数和惩罚参数的目标函数I。

FA-PMA-VMD算法的计算步骤为：

步骤1设置故障特征参数(频率重心为默认设置，用于计算萤火虫目标函数前通过PMA对获得的BIMF分量进行排序。其他故障特征参数根据实际的故障来设置)。

步骤2初始化萤火虫算法参数，最大吸引力β0、光吸收系数γ、步长因子α，给定群体规模m，指定迭代次数T。

步骤3随机初始化萤火虫的位置，计算萤火虫的目标函数I=Zm=F(k,α)作为各自最大荧光亮度In。

步骤4计算萤火虫的相对亮度和吸引度β[10]，吸引度公式如式(12)所示，根据相对亮度决定萤火虫的移动。

步骤5更新萤火虫的空间位置，对处于最佳位置的萤火虫进行随机扰动。

步骤6根据萤火虫的位置从新计算萤火虫的亮度。

步骤7判断是否满足终止条件，如果满足，跳出循环获得最优的全局极值点Zm和个体[k,α]。如不满足，则重复步骤3～步骤5直到满足循环终止条件。

步骤8根据前面确定的[k,α]，确定BIMF最终分量的个数，最后通过PMA获得按照所选的故障特征参数综合特征从强到弱排列BIMF分量。

2 仿真信号分析

在式(1)的信号中加入一个正弦信号n(t)=sin(2π120t)，如式(13)所示，作为输入信号,如图10所示。

S(t)=X(t)+n(t)

(13)

对输入信号S(t)用EEMD进行分解，对于幅值系数K和总体平均次数M的选取，Wu等[11]建议K由原信号的标准差乘以一个分数来定义，一般取原信号标准差的0.2倍。这样当M为一、两百次的时候，残留噪声引起的误差一般会处在一个比较低的水平(不足1%)。同时，他们还认为：在噪声水平合适的条件下，一味地增加执行次数对结果的改善并不显著。而反过来在一定范围内提高噪声水平对结果的影响也甚微，当然噪声太大也可能完全淹没信号的本质特征，使得分解毫无意义。本文中K取原信号标准差的0.2倍，M取值为100。

图10 加入谐波信号后的时域波形图

其结果如图11所示。可以发现分量之间出现了较为严重的频率混叠现象。

用FA-PMA-VMD方法对输入信号进行处理，首先初始化萤火虫算法的相关参数如表1所示。表1中：β0为最大吸引力;γ为光吸收系数;α为步长因子;n为群体的规模;T为迭代的次数。

表1 萤火虫算法的相关参数

图11 EEMD分解时域波形图

齿轮齿根裂纹故障会对齿轮的信号带来冲击，文献[12]表明峭度(Kurtosis，Kurt)对于冲击信号特别敏感，而均方根值(Root Mean Square，RMS) 能表明信号的强弱，多尺度模糊熵(Multiscale Fuzzy Entropy,MFE)为信号复杂度的量化统计指标[13]，因此都对齿根裂纹故障比较敏感。齿根裂纹故障信号为调幅调频信号，故本文将Kurt,RMS和MFE为故障特征参数。

按照FA-PMA-VMD方法的计算步骤，经过计算可以得到全局极点min(Imax)=0.009 2和最优个体值[k,α]=[4,2 325],计算结果如图12所示。多次计算后的结果如表2所示。

图12 萤火虫算法对k和α优化后结果

次数12345α2 3252 2972 3142 3312 330K44444

取五次计算后的平均值[4,2 319.4]作为优化后的最终结果，FA-PMA-VMD分解的最终分量的故障特征参数列的投影和Bk如表3所示。其分解结果如图13和图14所示。

对比图11和图13、图14，可以观察到FA-PMA-VMD对仿真信号的分解后，在效果优于EEMD，同时也可以观察到EEMD分解后的分量只是由能量的大小按照高频到低频排列，而FA-PMA-VMD分解后，将含有丰富故障特征的调幅调频信息的BIMF分量排在前面。

表3最终分量的故障特征参数列的投影和Bk值

Tab.3Bkvaluesofthefaultcharacteristicparametersofthefinalcomponent

BIMFii=1i=2i=3i=4Bi1.122 30.803 30.778 20.672 1

图13 FA-PMA-VMD分解分量时域波形图

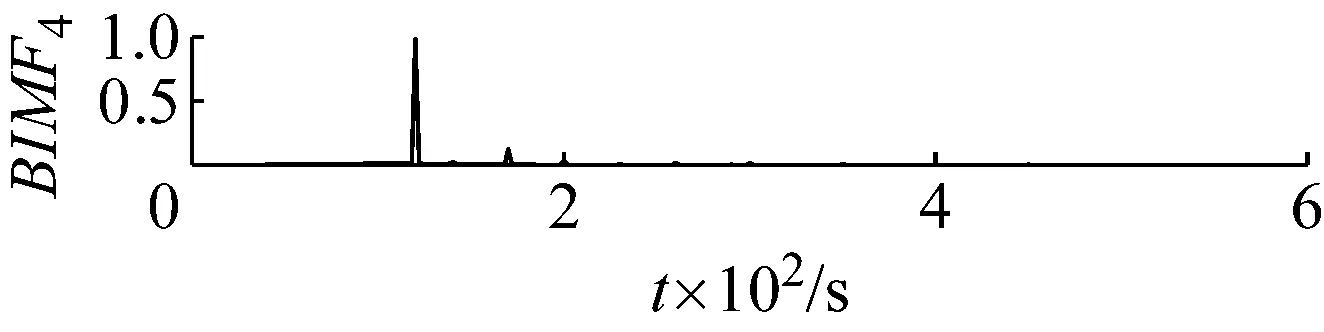
图14 FA-PMA-VMD分解分量频谱

Fig.14 Frequency spectra of the results decomposed by FA-PMA-VMD

3 实验信号分析

为验证本文方法对于振动信号分析的有效性，利用实际含有齿根裂纹的齿轮振动信号进行验证。

实验中齿轮为模数2.5 mm、齿数37的标准齿轮，齿根切割的裂纹宽度为0.15 mm，深度为20%。实验伺服电机主轴转速为 600 r/min，即转频为fr=10 Hz,啮合频率fz=370 Hz。实验采样频率为1 024 Hz，每次采样时间持续1 s。采集到的实验信号如图15所示。

图15 齿轮裂纹故障下的实验信号

用FA-PMA-VMD方法对实验信号进行分解，根据第2节仿真信号分析，选取RMS,Kurt,MFE为故障特征参数。最终分量的个数以及对应分量的故障特征参数列的投影和Bk如表4所示。分解结果如图16和图17所示。继续对BIMF2分量进行包络解调运算，并作出其包络谱如图18所示，其中特征频率及倍频处谱线幅值十分突出，说明特征频率信息被提取了出来并包含在BIMF2分量中。

表4最终分量的故障特征参数列的投影和Bk值

Tab.4Bkvaluesofthefaultcharacteristicparametersofthefinalcomponent

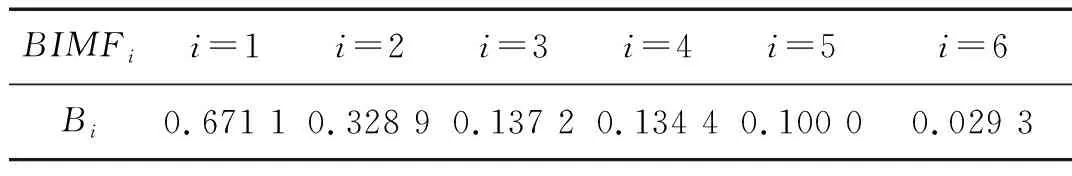
BIMFii=1i=2i=3i=4i=5i=6Bi0.671 10.328 90.137 20.134 40.100 00.029 3

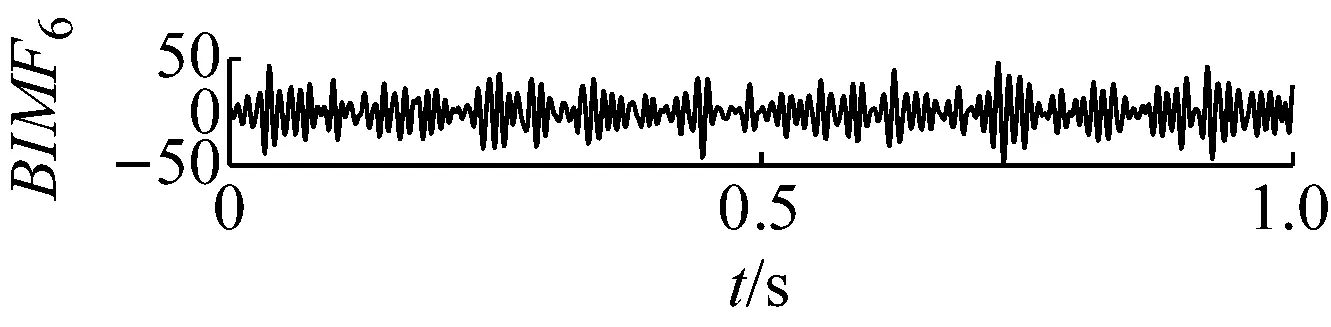
图16 BIMF分量的时域波形图

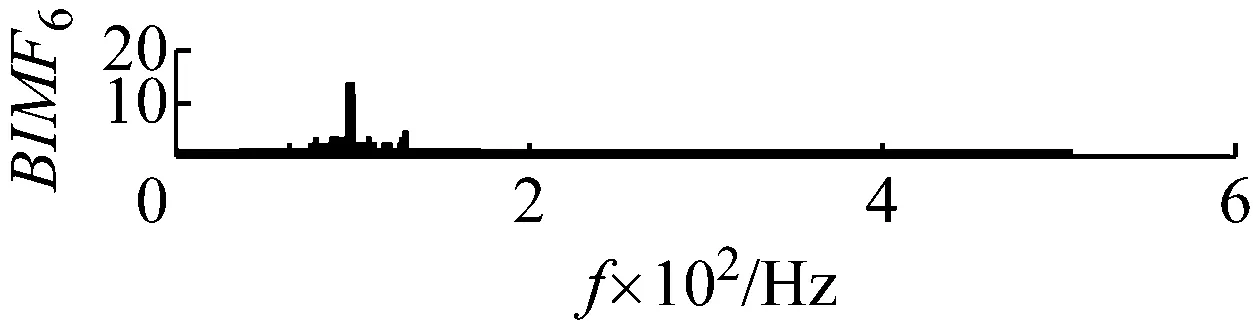
图17 BIMF分量的频谱

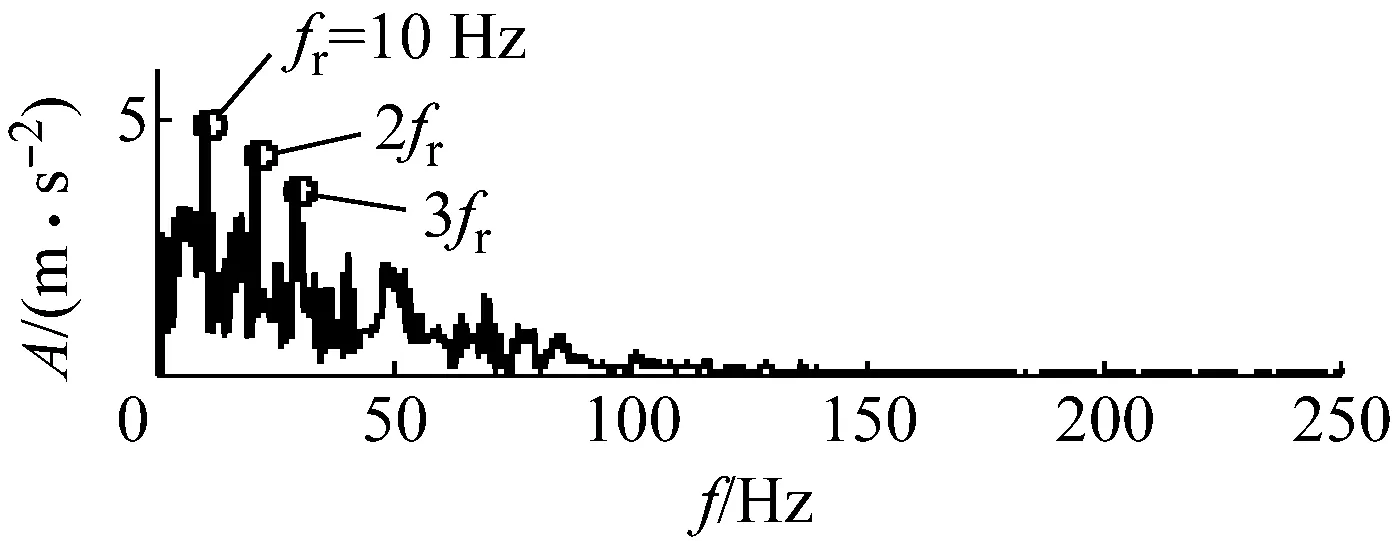
图18 BIMF2分量的包络谱

图19 20组实验信号中故障信息所在的BIMF分量及其个数

Fig.19 The BIMF components and the numbers of the fault information in the 20 experimental signals

为了进一步验证FA-PMA-VMD方法可以将含丰富故障信息的BIMF分量靠前排列，选取与实验信号同一测点但不同时间段获取的20组信号。用FA-PMA-VMD方法对这些信号进行分解。然后以故障信息所在的分量的排列顺序号为x轴，x对应的信号的个数(含有故障信息的同一顺序号的BIMF分量个数)为y轴建立直方图如图19所示。可以观察到这20组试验信号经过FA-PMA-VMD方法分解后获得的20组BIMF分量中，故障信息所在的分量主要集中在每组分量的前三项，表明FA-PMA-VMD方法可以将含丰富故障信息的BIMF分量靠前排列。