高坝泄洪诱发场地振动传播问题的有限元-无限元耦合分析
2018-08-27练继建李松辉
张 龑, 练继建, 李松辉, 刘 昉
(1.中国水利水电科学研究院 流域水循环模拟与调控国家重点实验室,北京 100038;2.天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
高坝大库工程是水资源综合利用和水能资源开发的需要,一直倍受世界各国重视。由于高坝大库泄洪落差大,巨大的下泄水体能量引起的水流脉动荷载作用在泄流结构上会诱发泄流结构产生振动,这种振动会传递至大坝场地浅层泥岩层,进而传递至周边场地,遇到特殊的场地条件,会对振动产生“放大效应”,对周边环境造成影响。一直以来,高坝泄洪引起振动问题主要局限于泄洪建筑物本身,其引起周边环境振动的研究鲜有报道[1]。然而,国内外有关高坝泄洪引起的周边环境振动,对建筑物的结构安全和人的身体心理产生影响已有事例,对其进行研究十分必要[2-4]。
泄洪诱发场地振动是水流荷载作用的振动能量以振动波形式向四周传播的过程,振动传播路径、传播过程中出现的振动放大和衰减效应等问题是重要研究课题之一。从结构振动系统组成来看,泄洪诱发场地振动属于振动“输入(泄流激励)-结构(泄流结构-场地振动传播系统)-输出(振动响应)”系统,振动传播过程实质上是对介质中的波动过程求解问题。采用有限元等数值分析方法建立实际场地的数学模型,是进行振动波传播特性问题分析的有效手段,如何真实模拟结构振动系统,是准确研究场地振动的前提。以往此类问题如轨道交通诱发场地振动的激励荷载形式较为单一且能量较为集中,对振动系统的研究范围较小(往往在百米量级),通过建立有限元模型进行求解时影响因素较少,因此可以达到较好的分析效果[5-7]。泄洪诱发场地振动是脉动水流流经不同泄流结构时产生的振动共同作用下复杂场地振动现象,振源成分和组成方式复杂;场地振动范围大(往往在千米量级),场地与大坝周围地形因素复杂(存在山体、河谷、水流等)[8]。通过有限元模拟会产生较大计算范围进行细密有限元网格划分后的计算求解问题和人工边界引起振动波的反射、散射等问题,加大数值分析难度的同时影响计算结果的可靠性。
鉴于此,为真实模拟多振源联合激励下大型复杂场地振动传播问题,本文引入“有限元-无限元”理论[9],并根据振源特性,研究多振源联合激励模拟方法,以期建立包含泄水建筑物、地基、周边场地土体以及无限半空间的多振源联合激励有限元-无限元耦合模型,分析高坝泄洪诱发场地振动的传播问题。
1 有限元-无限元耦合理论
1.1 波动问题无限单元法
无限单元法在研究无限域问题时近场用有限元模拟,远场用无限元模拟。该方法的实质是用有限元方法理论去研究有限单元外域单元的性态,起替代边界作用,使得受力体的真实位移及应力值不受有限区域网格影响。映射无限元法是在原有限元插值函数的基础上,对原有限元插值函数作变换,使得无穷远点为基函数的奇点[10-12]。
对三维空间无限域或半无限域进行模拟,需要用到3种空间无限元,即三维单向、三维双向以及三维三向的无限元,以包含所有无限区域。其中三维双向无限元可模拟地基土模型的棱边,三维三向无限元可用来实现对模型角点处的模拟。
(1) 三维n节点单向映射无限元只沿某一方向(假设沿ξ方向)延伸到无穷远
(1)
式中:ξ,η,ζ为局部坐标下任一点的坐标值。
(2) 三维n节点双向映射无限元沿其中两个方向(假设沿ξ和η方向)延伸到无穷远
(2)
(3) 三维n节点三向映射无限元沿3个方向都延伸到无穷远
(3)
图1所示为整体坐标系下一沿z向延伸至无限远的三维八节点无限单元,其中1号,2号,3号,4号节点即可与六面体有限单元耦合,该四节点组成的截面即为有限元、无限元的交界面,5号,6号,7号,8号为无限元的中间节点,9号,10号,11号,12号节点在无穷远处。实际无限域单元通过一组映射关系即可映射为局部坐标系下边长均为2的母单元。

图1 三维单向无限元
单元内任一点在局部坐标系和整体坐标系中的坐标变换为
(4)
式中:Mi为映射函数,其具体表达式为
(5)
位移模式为
(6)
式中:u,v,w为单元内沿x,y,z方向的位移;Ni为形函数,其具体表达式为
(7)
对三维空间棱边及角点部位的无限域问题,可以按常规的单向映射来处理,即对单元作特殊调整,把本来规则的单元变为形状不规则单元。但不规则单元不能很好地与周围单元协调,且不利于网格的自动生成,在实际建模计算中较为麻烦。双向及三向映射无限元可分别用来模拟三维空间棱边和角点的无限域,同时满足无穷远处位移等于零的条件。采用多向映射无限元应注意与其周围单元的协调,即要与相应的有限元耦合,还要与周围的单向或多向映射无限元保持协调。
图2为八节点双向映射无限元,可用来对空间模型中的棱边部位进行模拟。

图2 三维双向无限元
单元坐标变换为
(8)
式中:Mi为映射函数,其具体表达式为
(9)
位移模式为
(10)
式中:u,v,w为单元内沿x,y,z方向的位移;Ni具体表达式为
(11)
对三维空间角点部位的模拟,可以采用八节点三维三向映射无限元,如图3所示。与三向无限元相邻的单元既有八节点六面体有限元,又有八节点的单向及双向映射无限元。

图3 三维三向无限元
各节点在局部坐标系下的坐标值分别为
1(-1,-1,-1);2(0,-1,-1);3(0,0,-1);4(-1,0,-1);5(-1,-1,0);6(0,-1,0);7(0,0,0);8(-1,0,0)。
坐标映射函数
(12)
满足
(13)
位移模式为
(14)
式中:Ni具体表达式为
N7=(1-ξ2)(1-η2)(1-ζ2)
(15)
1.2 有限元-无限元理论耦合原理
利用有限元、无限元法求解地基土问题时,通常对地基进行有限元、无限元网格的划分,将求解域人为地分成不同的区域,对不同的区域可以采用不同的单元类型、不同的方法分别进行分析。近场可用有限元模拟,远场用无限元模拟,从而使一个连续的无限自由度问题变成离散的有限自由度问题。然后利用有限元和无限元在交界面上的力的平衡条件和位移的一致性,由此建立平衡方程,求解计算域内任意节点未知的位移及内力。耦合的一般过程如下:
(1) 近场、远场区域分别建立各自的方程
(16)
式中:{C}为待求变量;{F}为交界面相互作用力;上标1,上标2分别为有限元区域和无限元区域;下标1,下标2分别为在有限元、无限元域的解。
(2) 求出相邻区域交界面的位移表达式
(17)
(3) 建立交界面的连续方程
(18)
(4) 式(16)~式(18)联立求解,可得{C1},{C2}。然后代入各原始算式求解{U1},{U2}以及应变、应力分量。
1.3 动力平衡方程及分析方法

(19)

2 场地振动案例简介
以国内某高坝为研究背景,该坝为混凝土重力坝,坝顶高程384.00 m,最大坝高162.00 m,坝顶长度909.26 m,正常蓄水位380.00 m,校核洪水位381.86 m,死水位及汛限水位370.00 m。坝身由12个表孔和10个中孔组成,采用表中孔间隔布置形式,由中导墙分割成两个对称的消能区,属于典型的高坝底流消能的布置形式。电站自2012 年10 月12 日开始中孔开闸泄洪,期间出现中孔启闭机室声振、塔带机立柱振动,县城部分门店卷帘门晃动、民居及校舍的门窗响动、家具颤动、吊灯摆动等现象。经初步测明,水电站距下游县城区距离最近处仅为0.5 km,最远可达2.5 m,城区场地土体构成形式多样,下游县城靠近右岸山体一侧场地振感明显,存在振动放大现象。
根据下游场地的地质勘探成果:下游场地表面为砂层覆盖层,下部为场地浅层的泥岩层。下游主城区靠近右岸山体一侧存在一条古河道,平均宽度200 m左右,古河道上的覆盖层最大厚度达80 m。与之相比,主城区其他区域的场地覆盖层厚度明显较小。不同区域位置如图4所示。

图4 水电站坝区与周边场地示意图
3 数值模型的建立
3.1 有限元模型
有限元模型依据实际工程结构,运用计算软件ABAQUS建立包括泄水建筑物、场地浅层及深层结构有限元模型。泄水建筑物包括溢流坝、导墙、水垫池及二道坝。场地土体尺寸根据地质资料进行建立。计算时整体模型均视为弹性体,不考虑塑性变形,场地有限元模型及大坝有限元模型如图5所示。
(1) 材料参数
根据相关设计报告和地质勘探资料,整个模型按材料类型可分为4部分:混凝土大坝,下游场地表层覆盖层,下游场地浅层泥岩,深层砂岩层与两岸山体为砂岩。详细的材料参数取值见表1。
(2) 单元尺寸
对于复杂的大范围模型,有限元网格划分的粗细往往存在一定的盲目性,粗糙的网格难以保证计算精度,但网格尺寸越小,整体模型的计算规模将指数增长。一般情况下单元网格在振动波传播方向的尺寸与所考虑的最短波长比值不应大于1/8~1/6,当网格划分满足最小波长包含4个单元时,有限元计算结果与解析解误差较小,但是在高频范围偏差增大;当网格划分满足最小波长包含8个单元时,有限元计算结果与解析解吻合较好[13-14]。

(a) 整体模型

(b) 坝体模型

材料分区材料类型动弹模/MPa密度/(kg·m-3)泊松比剪切波速/(m·s-1)大坝混凝土45 0002 4500.20下游场地表层覆盖层砂层及砂卵石层601 6700.38400下游场地浅层泥岩层泥岩902 1250.391 000深部砂岩层及山体砂岩11 3002 5800.3252 600
根据原型地质勘探及原型观测资料,实测最小剪切波速为400 m/s,主要在场地表层覆盖层,下游场地各测点的主频主要在2.0 Hz左右。因此考虑有限元模型中典型短波波长取值为200 m,同时考虑一个波长至少包含8个单元,确定出模型场地表层覆盖层部分最小网格尺寸,依次类推,可得到模型其他区域的网格划分最小尺寸要求。
3.2 有限元-无限元耦合模型
以大坝结构(振源)为极点,建立三维映射无限元模型。取无限元近点到远点的距离与近点到极点的距离相同,模型范围包括模拟除山体以外场地无限域空间,即以下游场地浅层泥岩层、深部砂岩层及两岸山体上表面为自由面,深部砂岩层底面与侧面均用无限元模拟。无限元单元类型为CIN3D8,无限元材料类型与深部砂岩层及山体一致。通过建立独立的无限元网格,再将无限元网格和有限元网格绑定,实现有限元-无限元相互耦联。无限元模型如图6所示,有限元-无限元耦合模型如图7所示。

图6 场地无限元模型

图7 场地有限元-无限元耦合模型
根据模型试验和原型观测成果,高坝泄洪水流脉动荷载的频带范围大致在0~2.0 Hz,主频在1.0 Hz左右,诱发的坝体及消力池结构基础的振动响应主频也在2.0 Hz左右。结合以往资料综合考虑[15],数值计算时间步长取0.02 s,即模型上荷载的奈奎斯特截止频率为25 Hz,计算时间与原型观测一致,即120 s。
3.3 大坝自振特性分析
对大坝的准确模拟是研究场地振动传播问题的前提,通过特征系统实现算法(Eigensystem Realization Algorithm, ERA)[16-17]对泄流工况下坝肩测点振动信号进行模态参数识别(包括固有频率、阻尼比和模态振型),识别出的大坝结构工作状态下前4阶振动频率、阻尼比与有限元-无限元模型计算的大坝结构前4阶振动频率、阻尼比见表2,振型图如图8所示。

表2 模态参数识别结果
可以看出,通过有限元-无限元模型计算得到大坝结构前4阶振动频率与实测信号识别结果接近,误差在10%以内。而且,由于在实际情况中结构均要与水接触,结构振动频率应比以上有限元计算结果略小。因此,模型可以有效模拟坝体结构实际运行情况。
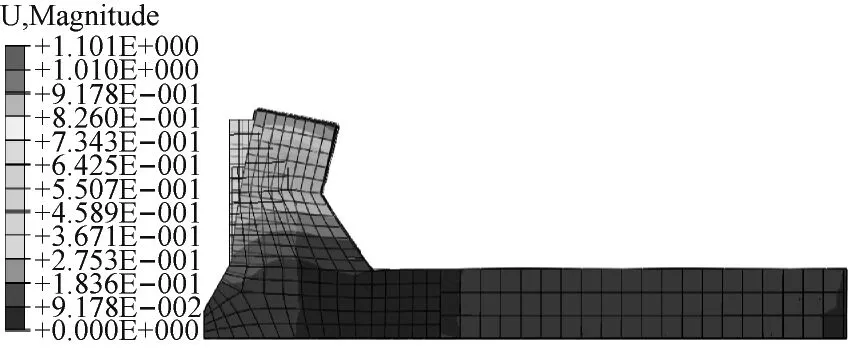
(a) 一阶振型

(b) 二阶振型

(c) 三阶振型

(d) 四阶振型
4 动力荷载输入
“动力荷载”输入系统即振源激励系统。计算采用原型观测下不同泄流工况泄流结构处水流脉动荷载时域信号作为动力输入,加载方式为面压加载。由于实测数据为点脉动压强,因此加载时对点脉动压强换算至平均面脉动压强[18-19]。引起结构及场地振动的能量主要来自脉动水流流经泄流结构时产生的振动叠加,即孔口脉动荷载(表孔和中孔)、消力池底板脉动荷载、导墙脉动荷载、尾坎脉动荷载以及跌坎脉动荷载[20]。各处荷载源产生能量的大小以及振动特性都有所区别,而实测的水流脉动信号体现的是荷载源相互影响和作用后不同振源独立的振动特性,因此在计算过程中,将引起场地振动的5个激励源视为5个独立的、不相关的等效荷载,加载时分别按照同一股水流流经泄水建筑物不同位置的时间差采集信号和同时采集信号两种方式加载。6种加载方式如图9所示。

(a) 表孔加载

(b) 中孔加载
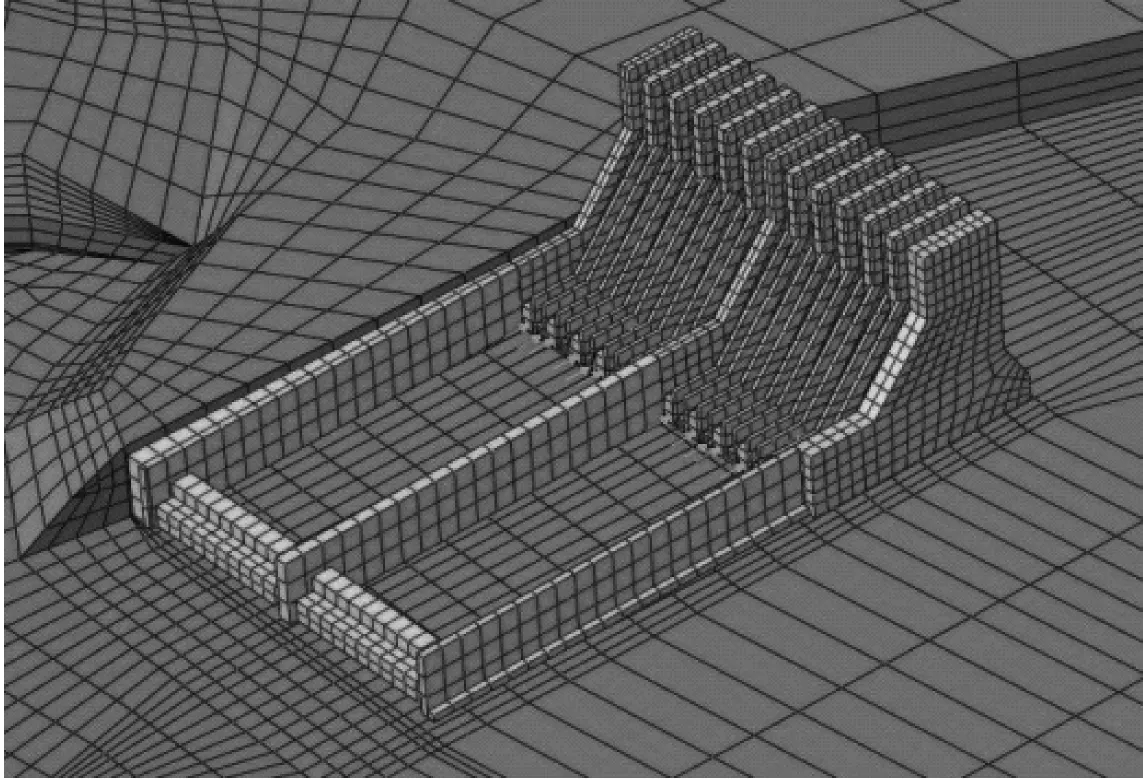
(c) 跌坎加载

(d) 导墙加载

(e) 底板加载

(f) 尾坎加载
5 模型有效性验证
原型观测资料显示,场地振动特性根据场地土体组成的不同分为两种类型:振动能量被放大的古河道区域和振动能量衰减的非古河道区域。因此,选取场地振动强度较大泄洪工况:1#~10#中孔局开3.5 m,1#~12#表孔局开5.85 m,上游水位379.79 m,下泄洪水流量10 560 m3/s进行计算。在古河道区域和非古河道区域分别沿水流方向选取5个测点,考察通过有限元模型与有限元-无限元耦合模型计算的场地振动响应特性。测点位置与编号如图10所示。对应模型输出点如图11所示。图12为有限元模型与有限元-无限元耦合模型计算的下游场地区域总体加速度云图。

图10 不同区域路线及测点编号
可以看出,两个模型古河道区域振动强度均大于非古河道区域,与原型观测结果相似。有限元模型场地表面振动强度对比并不明显,有限元-无限元耦合模型振动传播路径相对清晰。选取古河道区域与非古河道区域各测点,分析其顺河向和垂向振动强度变化情况,振动强度通过振动加速度振动标准差表示(下同),其计算公式为

图11 模型对应输出点示意图

(a) 有限元模型结果(b) 有限元-无限元耦合模型结果
图12 场地区域振动加速度云图
Fig.12 Vibration acceleration of the ground
(20)
式中:xi为每一时刻振动加速度数据;N为数据个数;μ为整个采集时间振动加速度的算术平均值。
图13和图14分别为两种数值模型与原型观测顺河向与垂向振动强度结果。

(a) 顺河向
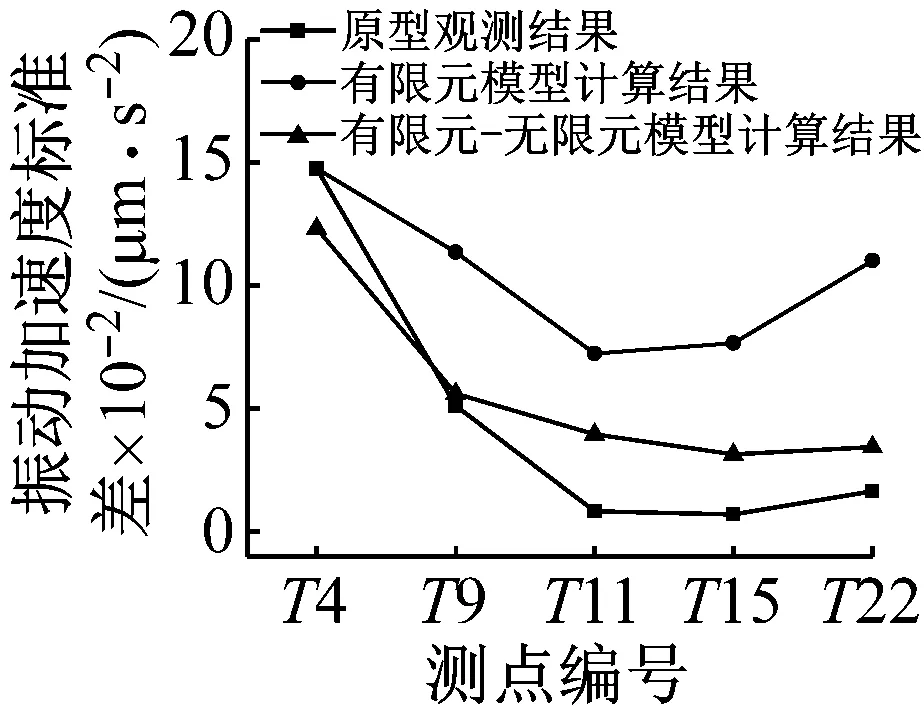
(b) 垂向

(a) 顺河向

(b) 垂向
从图13和图14可以看出,两种数值模型总体能够反映场地各个方向的振动变化特性。但是,有限元模型计算结果总体偏大,而且古河道区域靠近边界处T15,T22测点以及非古河道区域下游的T20,T23测点,由于边界问题,振动波回波等因素影响,各向振动变化规律与实际不符。有限元-无限元耦合模型计算各向振动标准差略大于实测观测结果,各个位置处的振动变化规律与实际更为接近,振动波传递至模型边界处,无回波现象,振动强度变化与原型观测结果一致。
以场地测点T9与T12为例,对比原型观测与数值模型计算得到的场地振动响应频谱特性。古河道区域T9测点顺河向和垂向振动加速度功率谱如图15所示。
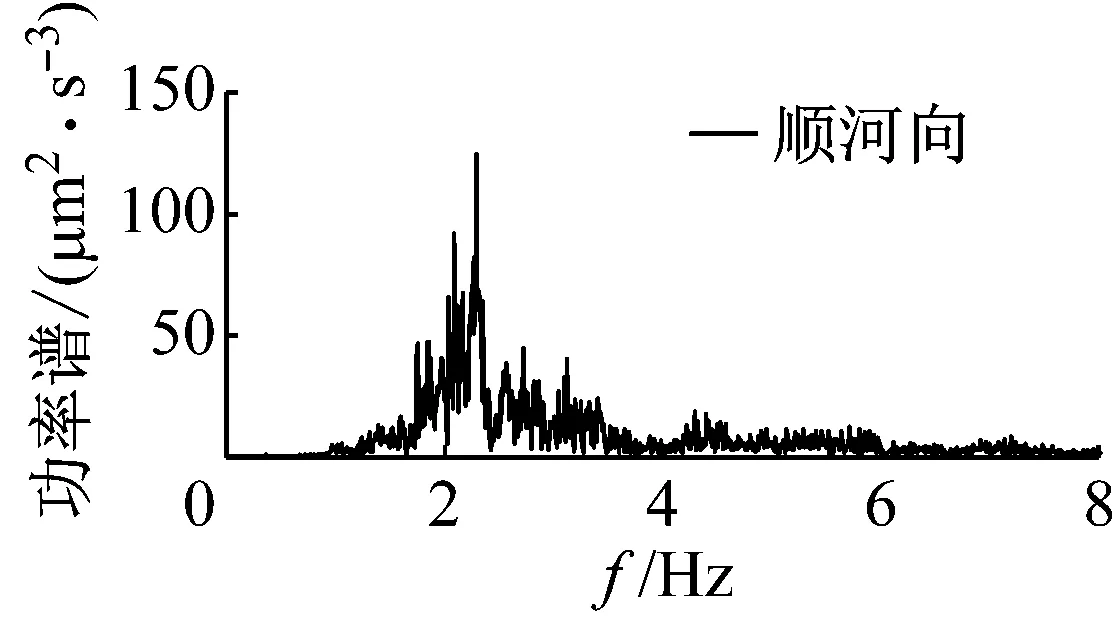

(a) 原型观测结果


(b) 有限元模型计算结果


(c) 有限元-无限元耦合模型计算结果
图15T9测点各向振动加速度功率谱图
Fig.15 Power spectrum of vibration acceleration ofT9
原型观测结果可以看出,T9测点振动频谱特性总体为能量集中于一个或多个区间,并在各个区间存在明显峰值的窄带噪声谱,顺河向振动能量集中在0.5~2.35 Hz以及2.35~4.0 Hz两个频率区间,振动主频为2.44 Hz,另一优势频率为3.23 Hz。垂向振动能量区间较顺河向宽,在0~6.0 Hz内都有能量分布,两个主要能量区间为0.5~3.0 Hz和3.0~6.0 Hz,振动主频为3.26 Hz,另一优势频率为2.44 Hz。
从数值计算结果来看,有限元模型计算得到T9测点顺河向振动能量分布于0.5~4.0 Hz,主频为2.54 Hz,且无其他优势频率,振动能量分布与原型观测数据不同,且主频偏大;垂向振动能量分布于0~2.4 Hz及2.4~3.5 Hz两个区间,区间范围小于原型观测结果,振动主频为2.55 Hz,无其他优势频率。有限元-无限元耦合模型计算得到T9测点顺河向和垂向振动的两个能量分布区间与原型观测结果较为一致,振动主频分别为2.41 Hz和2.52 Hz,计算结果同时体现其他优势频率。
非古河道区域测点T12各向振动加速度功率谱如图16所示。


(a) 原型观测结果


(b) 有限元模型计算结果


(c) 有限元-无限元耦合模型计算结果
原型观测结果可以看出,T12测点振动特性与T9测点不同。顺河向振动能量依然集中于0~3.2 Hz和3.2~5.0 Hz两个区间,但3.2~5.0 Hz的能量较小。垂向振动能量分布较为集中,主要能量区间为1.5~3.0 Hz。两个方向的振动主频都为2.41 Hz。
从数值计算结果来看,有限元模型计算得到T12测点顺河向振动能量集中在1.5~3.0 Hz,振动主频为2.07 Hz;垂向振动有1.5~2.5 Hz和2.5~3.0 Hz两个主要能量区间,振动主频也为2.07 Hz,计算结果与原型观测结果有一定差别。有限元-无限元耦合模型计算得到的顺河向和垂向振动能量分布和主频(2.39 Hz和2.54 Hz)与原型观测非常接近。
6 场地振动特性分析
对有限元-无限元模型运用上述振源加载方式,分析泄洪工况下,下游场地振动的传播规律。选取模型下游场地6个典型的横断面和5个典型的纵断面,研究下游场地的振动传播分布情况。其中,Z1表示纵断面1,H1表示横断面1,其余断面的标注依次类推。测点位置见图17,断面及水平面测点编号见图18。选取T9测点及其垂直向下距离间隔为50 m的4个测点,分析振动垂向传播规律,测点位置及编号如图19所示。
6.1 振动强度分布
6.1.1 场地振动沿水平面变化规律
多振源联合激励下,模型5个纵断面的振动强度分布情况如图20所示。

图17 模型场地振动测点布置图
由下游场地纵向振动强度分布可知,在各个纵断面上,随着振动波在下游场地中传播距离的增加,场地在各方向的振动逐步衰减。其中纵断面1,断面3,断面4,断面5衰减规律相似,振动在传播初期衰减明显,随着传播距离的增加,衰减速度逐渐减慢;纵断面2在振动传播初期衰减缓慢,随着传播距离的增加,振动衰减加剧。由于纵断面1靠近下游场地与右岸山体交界处,泥岩层坚硬,衰减最为平滑;纵断面2沿下游场地古河道位置的中线布置,覆盖层厚度最大,振动强度最大,衰减规律与其余断面不同,在场地的中段位置出现振动放大现象;纵断面3位于下游场地古河道的左边界位置,纵断面4为下游场地非古河道区域的中线,两个断面覆盖层厚度接近,振动强度和衰减规律最为相似,振动传递到22#和23#两个测点时,振动有所放大;纵断面5为下游河道与场地交界处,除20#点振动有所增大外,传播规律与纵断面1相似,但振动强度小于纵断面1。另外,场地中部的纵断面3和纵断面4顺河向振幅最大,垂向振幅最小,场地两侧的纵断面1和纵断面5以及古河道处纵断面2的各向振动情况与之相反。

(a) 断面和断面编号

(b) 测点编号

图19 T9测点处垂直向测点编号
模型前5个横断面的振动强度分布情况见图21。
由下游场地横向振动强度分布可知,各个横断面古河道区域测点振动强度较大,非古河道区域振动有所衰减,这一点在非古河道中线处体现的更为明显。横断面1和横断面2的振动分布相似,古河道横断面区域振动强度基本相同,场地右岸离坝区较近,受水流影响,振动强度较大;横断面3处古河道中心线处振动强度最大,振动从古河道中心线向两侧衰减;横断面4处振动强度最大处向古河道中心线右侧偏移,振动传递到横断面5处,振动强度最大测点重新回到古河道中心线处。另外,各横断面顺河向振动强度最大,垂向振动强度最小。

(a) 纵断面1

(b) 纵断面2

(c) 纵断面3

(d) 纵断面4

(e) 纵断面5
图20 下游场地纵断面振动强度分布
Fig.20 The vibration intensity distribution of longitudinal sections
6.1.2 场地振动沿垂向变化规律
多振源联合激励下,场地振动垂向传递规律如图22所示。
可以看出,振动垂向传播过程中,在0~100 m时振动强度较大且有所波动,甚至在100 m处振动有所增大,超过100 m后振动强度迅速减小。这是因为T9测点所在古河道区域覆盖层较厚,厚度超过80 m,因此场地振动容易激励土体产生自振,导致振动放大,当振动从覆盖层传递至场地浅层的泥岩层后,振动迅速衰减。

(a) 横断面1

(b) 横断面2

(c) 横断面3

(d) 横断面4

(e) 横断面5

图22 T9测点处振动强度垂向分布
6.2 振动频率特性
6.2.1 场地振动沿水平面变化规律
从振动强度分布来看,古河道区域中心线处纵断面2与其余断面呈现两种传播变化规律,因此,以该断面和非古河道中心线处纵断面4为例,研究场地振动传播过程中的频谱变化规律。纵断面2各方向加速度功率谱沿下游变化如图23所示。
可以看出,随距离的增加,各个测点顺河向和横河向振动频谱分布和变化规律比较一致,振动能量集中在0.5~4.0 Hz,频带较宽,振动向下游传播过程中,振动能量有越来越集中的趋势(主要能量频带变窄),但这一趋势并不明显。垂向振动能量有两个明显频带区间,即2.0~3.0 Hz和3.0~4.0 Hz,随着振动向下游传播,两个频带区间不随距离增大并不改变。总体来看,各方向的低频振动能量总体随着距离的增加而衰减,当传播至3 000 m左右时,出现一振动能量峰值。
纵断面4各方向加速度功率谱随下游变化如图24和所示。
该区域顺河向主要振动能量频带分布与古河道区域一致,都为0.5~4.0 Hz,但随距离的增大,振动能量迅速向2.5 Hz处集中。横河向与垂向振动频谱特性与古河道区域有所区别,振动初始状态振动主要频带都为0.5~4.0 Hz,但传播至1 000 m后,振动变为主要频率集中在2.5 Hz和3.3 Hz左右的,具有明显峰值的振动形式。该区域振动能量随距离衰减更为平缓。
6.2.2 场地振动沿垂向变化规律
场地振动沿垂向传播过程中的振动加速度功率谱变化如图25所示。
可以看出,振动垂向传播过程中频谱分布较为一致,优势频带集中在2.0~3.0 Hz和3.0~4.0 Hz,频谱分布与古河道纵断面2垂向振动向下游传播一致。振动传递至150 m后,振动能量衰减迅速,其中3.0 Hz以下振动能量表现的更为明显。
7 结 论
文章根据有限元-无限元原理,研究建立包含泄水建筑物、浅层泥岩层、深部砂岩层、周边山体以及模拟无限半空间的有限元-无限元耦合模型方法和多振源联合激励模拟方法,分析多振源联合激励下泄流诱发场地振动传播规律,并得出以下结论:

(a) 顺河向

(b) 横河向

(c) 垂向

(a) 顺河向

(b) 横河向
(1) 将同时采集到的引起场地振动的5处激励源视为5个独立的、不相关的等效荷载,并分别进行独立加载建立的动力输入系统较为合理。这种加载方式下,通过无限元来处理边界条件与有限元的固定边界相比,前者能让振动波在边界上不发生反射,计算得到土体振动幅值与原型观测更为接近,同时振动频谱特性和振动主频都与原型观测结果相似。

(a) 传播距离0 m

(b) 传播距离50 m

(c) 传播距离100 m

(d) 传播距离150 m

(e) 传播距离200 m
图25T9测点处垂向测点振动加速度功率谱图
Fig.25 Vibration acceleration power spectrum of vertical distribution measuring points atT9
(2) 不同断面场地振动水平传播规律并不一致,古河道区域场地振动强度相对较大,传播初期振动强度变化不大,后期衰减迅速;其余区域振动强度较小,振动传播初期振动衰减迅速,随着距离的增加,衰减变得缓慢。从频谱分布来看,场地振动能量初期大多为0.5~4.0 Hz的宽频振动,随着振动向下游传播过程中,振动能量频带越来越集中,且低频能量衰减迅速,其中非古河道区域较古河道区域集中速度更快。
(3) 场地振动垂向传播过程中,覆盖层处的振动强度在同一个量级波动,振动传递至场地浅层的泥岩层后强度迅速减小,传递至深部砂岩层后,振动强度可忽略不计。从频谱特性来看,场地表面振动频带较宽,随着振动垂向传播,频带逐渐变窄,且低频逐渐被土体过滤。
