基于一次性合龙方式的多跨连续刚构桥梁顶推力

马玉荣, 陈海波, 吕改锋, 陈恒大

(1. 安徽新华学院, 安徽 合肥 230088; 2. 江苏交科交通设计研究院有限公司, 江苏 南京 210002; 3. 安徽建筑大学, 安徽 合肥 230601; 4. 陕西省土地工程建设集团, 陕西 西安 710075)

连续刚构桥梁因其较好的经济性能、优秀的跨越能力和轻盈雅致的外观得到工程师的青睐.多跨连续刚构桥梁,在沟壑纵横的西部地区有着巨大的应用潜力.连续刚构桥梁的挂篮现浇工艺比较成熟,但跨中合龙段的高程控制和顶推力确定仍然比较困难.尤其是有些多跨连续刚构桥梁需要一次性合龙,对工程设计和施工提出了更高的要求.文献[1]通过变换墩身高度、主跨长度、收缩徐变时间等因素对连续刚构桥梁的合龙顶推力进行了研究,建议收缩徐变时间取10 a即可.文献[2]对多跨连续刚构桥梁的合龙顺序进行了深入的研究,从结构受力角度得出了中跨—次中跨—次边跨—边跨的合理合龙顺序.文献[3]对多跨预应力混凝土连续刚构桥梁合龙方案进行了研究,提出为了施工方便,可以考虑边跨—次边跨—次中跨—中跨的合龙顺序.文献[4]以合龙时的两悬臂端的竖向位移为指标,推导出连续刚构桥梁跨中成桥预拱度估算公式,从而反推出合龙顶推力.文献[5]研究了多跨连续梁的合龙顺序,考虑施工阶段便利因素和设计阶段受力因素,分析了最优合龙顺序.文献[6]对大跨径连续刚构桥梁的合理加载龄期进行了研究,充分考虑了温度应力及收缩徐变对连续刚构桥梁合龙时的影响,从而得出相应的合龙顶推力.

综上所述,有关连续刚构桥梁的合龙顶推力的研究大多是通过有限元仿真模拟的方式进行,很少有合龙顶推力理论公式的推导,和对公式进行工程实例验证.因此,本文依托某多跨连续刚构桥梁,推导了不同温差条件下的合龙顶推力理论公式,并选取工程实例进行了有限元模型的验证,系统研究了基于一次性合龙方式的连续刚构桥梁合龙顶推力求解方法,为今后多跨连续刚构桥梁的合龙顶推力计算提供了参考.

1 工程背景

某桥是210国道川口至耀州段公路改扩建工程的一座特大桥梁,其主桥结构形式为预应力混凝土连续刚构体系,跨径组合为(62.5+4×115.0+62.5) m,纵、横、竖三向预应力体系.桥梁平面位于直线上,纵面位于0.63%的上坡(起点附近位于凹型竖曲线上),桥宽12.0 m.箱梁采用单箱单室截面,顶板宽12.0 m,底板宽6.5 m,翼缘板悬臂长为2.75 m.箱梁根部梁高6.5 m,高跨比为1/17.7;跨中梁高2.8 m,高跨比为1/41.1;根部底板厚0.9 m,跨中底板厚0.32 m;梁高及底板厚度均按2次抛物线变化.主梁采用C55混凝土,墩身采用C40混凝土.主桥箱梁采用悬臂浇筑法施工,采用边跨、次中跨及中跨一次性合龙的合龙顺序.该桥的立面布置如图1所示.

图1多跨连续刚构桥梁
Fig.1 Multi-span continuous rigid frame bridge

2 有限元模型的建立

对墩梁固结的连续刚构体系,由于超静定次数多,合龙温差和砼的收缩徐变等因素引起结构次内力,产生结构内力重分布和结构变位的非线性,而且是变截面箱梁,依靠手算很难得到精确解.因此本文采用专业桥梁计算软件MIDAS /Civil,按照施工顺序采用正装计算法对施工过程进行模拟分析计算.

建模过程中,C55混凝土弹性模量取35.5 GPa,材料密度取2 600 kg·m-3.混凝土收缩徐变采用现行规范提供的计算公式计算变形与预应力损失.主梁划分为218个梁单元,5个主墩划分为75个梁单元;边界条件模拟为:主梁与墩顶刚性连接,5个主墩墩底固结,过渡墩支座模拟成活动铰支座,只约束竖向位移.模型建立时去除临时墩,有限元模型如图2所示.

图2多跨连续刚构桥梁有限元模型图

Fig.2 Finite element model diagram of multi-span continuous rigid frame bridge

3 合龙顶推力分析

由于连续刚构桥是墩梁固结结构,在载荷作用引起竖向挠度的同时,也会使主墩产生相对水平位移,造成主墩偏位,对主墩受力产生不利影响.为了消除此影响,在连续刚构桥合龙时对梁体施加一个水平顶推力,给主墩施加一个反向位移来抵消合龙温差、后期收缩徐变等因素引起的主墩水平位移.本文按消除墩顶水平位移的思路计算合龙时的顶推力.

3.1 墩顶水平位移的确定

在合龙顺序确定的情况下,墩顶水平位移主要考虑因结构体系转换、长期载荷作用下混凝土收缩徐变及实际合龙温度与设计合龙温度的合龙温差等因素引起的水平位移.

(1) 混凝土收缩徐变引起的墩顶水平位移.对结构进行有限元分析计算时,考虑施工阶段在长期载荷作用下13#～17#墩墩顶的水平位移.为了确定桥墩在正常合龙工况下收缩徐变引起的相对变位,收缩徐变终止时间设定为3 650 d(约10 a).计算出在合龙时不施加顶推力的情况下各墩墩顶在收缩徐变10 a后各墩顶的水平位移,由于墩身中非预应力钢筋的作用,收缩徐变10 a后一般不能达到模型计算值.本文分别选取墩顶100%、70%、30%的水平位移值作为参考.具体结果见表1,相应的水平位移如图3所示.

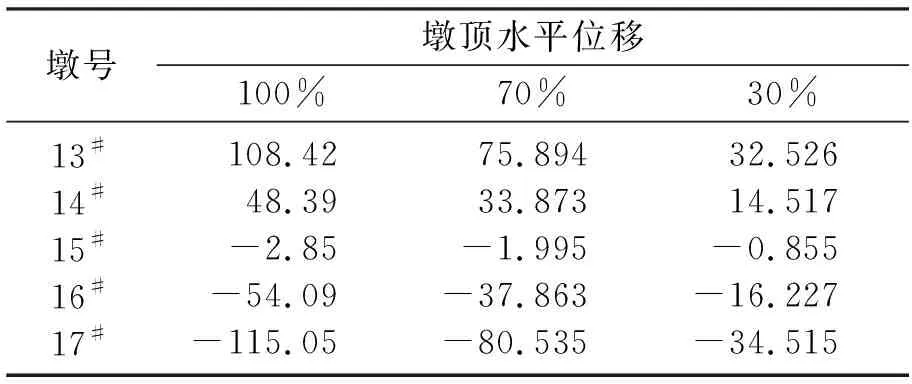
表1 收缩徐变10 a后桥墩墩顶水平位移

注:表1～表4中数字正数表示向右侧变形,负数表示向左侧变形.

图3 收缩徐变10 a后桥梁结构位移图Fig.3 Displacement diagram of bridge structure after a decade of shrinkage and creep

(2) 温差引起的墩顶水平位移.实际合龙温度往往与设计合龙温度有一定差值,由于桥梁合龙后升温较降温对结构受力有利,故尽量选择低温合龙.但由于各种客观因素导致实际合龙温度比设计合龙温度高,则必须采取预顶推来消除合龙后降温导致的不利效应.

为了分析实际合龙温度比设计合龙温度高时对结构的影响,计算了10个升温值对主梁部分控制截面各节点的水平位移,见表2.

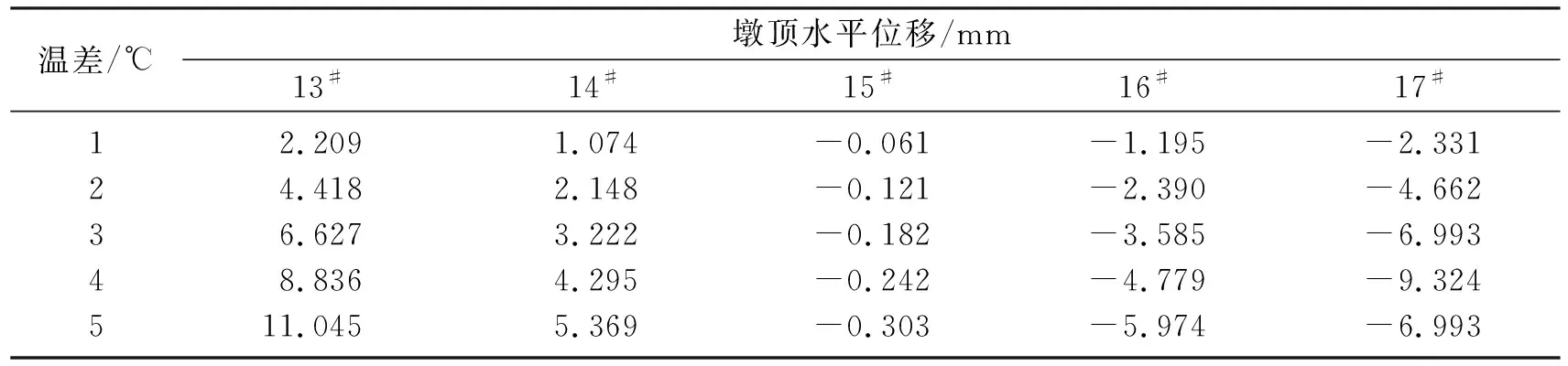
表2 实际合龙温度与设计合龙温度的温差作用下桥墩墩顶水平位移Table 2 The horizontal displacement of the pier of temperature difference between the actual and design

由表2分析可知,温度变化与各节点水平位移呈线性比例关系,同时也得知,升温使得各节点的水平位移方向与收缩徐变产生的各节点水平位移方向相反,因此若合龙温差不为零,就要使各节点产生水平位移,就必须采取预顶推的方法消除合龙温差产生的效应.若实际合龙温度高于设计合龙温度,即在高温状态下合龙,则要增大顶推力抵消合龙后合龙温差产生的不利降温效应.

3.2 单位顶推力作用下的墩顶水平位移

在有限元计算中,需在最大悬臂工况下(即中跨合龙前)对悬臂端纵向施加的水平推力消除表1、表2中各墩顶产生的水平偏位.

在次中跨顶推位置处分别施加0、100、200、300 kN的顶推力,各墩顶处的水平位移见表3.

表3 次中跨施加顶推力时墩顶水平位移Table 3 The horizontal displacement of the pier when exerting jacking force on the side span

从表3分析可知,在次中跨顶推位置处施加顶推力时,各墩墩顶水平位移变化与顶推力呈线性变化,即每施加100 kN的顶推力,13#墩顶水平偏位约-8.163 mm,14#墩顶水平偏位约5.947 mm,15#墩顶水平偏位为0,16#墩顶水平偏位-6.531 mm,17#墩顶水平偏位9.455 mm.

在中跨顶推位置处分别施加0、100、200、300 kN的顶推力,各墩顶处的水平位移见表4.

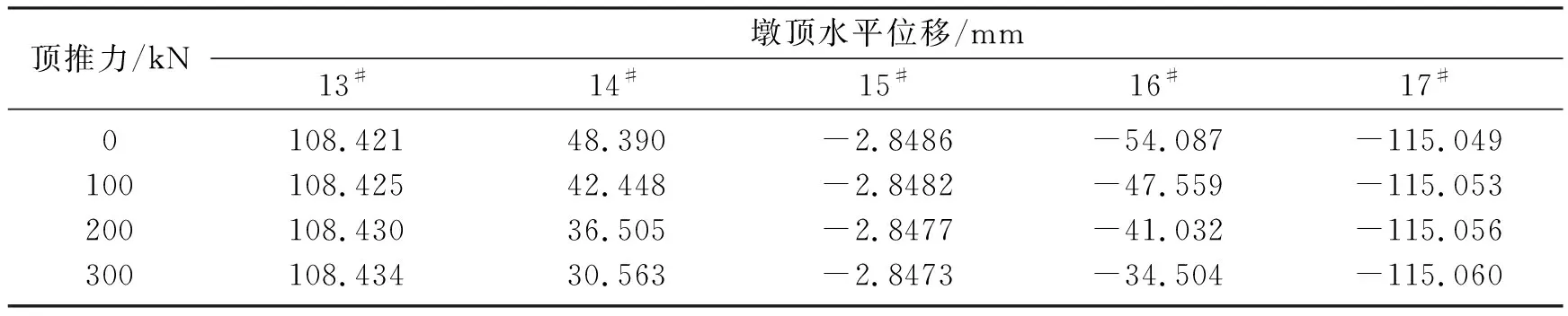
表4 中跨施加顶推力时墩顶水平位移Table 4 The horizontal displacement of the pier when exerting jacking force on middle span

从表4中分析可知,在中跨顶推位置处施加顶推力时,各墩墩顶水平位移变化与顶推力呈线性变化,即每施加100 kN的顶推力,13#墩顶水平偏位约0.004 mm,14#墩顶水平偏位约-5.942 mm,15#墩顶水平偏位约0.000 4 mm,16#墩顶水平偏位约6.528 mm,17#墩顶水平偏位约-0.004 mm.

3.3 顶推力估算公式推导

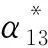
(1) 抵消收缩徐变水平位移的顶推力.以13#、14#墩因收缩徐变引起的70%墩顶的水平位移为控制目标量,所需要的顶推力需要满足式(1)、式(2).

联立式(1)、式(2)解得:α13=9.305;α14=15.013.

以16#、17#墩因收缩徐变引起的70%墩顶的水平位移为控制目标量,所需要的顶推力需要满足式(3)、式(4).

联立式(3)、式(4)解得:α16=14.328;α17=8.524.

次中跨因抵消收缩徐变产生的水平位移所需要的顶推力为

(5)

中跨因收缩徐变产生的水平位移所需要的顶推力为

(6)

(2) 抵消合龙温差产生的水平位移的顶推力.当设计合龙温度与实际合龙温度的温差为Δt时,以13#、14#墩因合龙温差引起的墩顶的水平位移位控制目标量,则所需要的顶推力需要满足式(7)、式(8),其中Δt只取数值,无量钢.

(9)

中跨因合龙温差产生的水平位移所需要的顶推力为

(10)

当给出设计温度与实际合龙温度的温差Δt为5、10和15 ℃时,根据式(9)、式(10)得出因抵消合龙温差产生的水平位移所需要的顶推力,如表5所示.

表5 抵消合龙温差产生的水平位移所需顶推力

(3) 顶推力求解.在结构上实际施加的顶推力要抵消合龙温差和收缩徐变产生的总水平位移,最终顶推力为所求得的2部分顶推力之和.即:

当给出设计温度与实际合龙温度的温差Δt为5、10和15 ℃时,根据式(11)、式(12)得出总顶推力的理论值,如表6所示.

表6 施加在结构上的顶推力的理论值

为了施工的方便和可操作性,给出以下在结构上实际施加的顶推力的建议值,如表7所示.

表7 施加在结构上的顶推力的建议值

4 工程实例验证

当Δt取5 ℃时,在次中跨、中跨分别施加1 000、1 700 kN的顶推力.结构应力计算结果如图4所示.

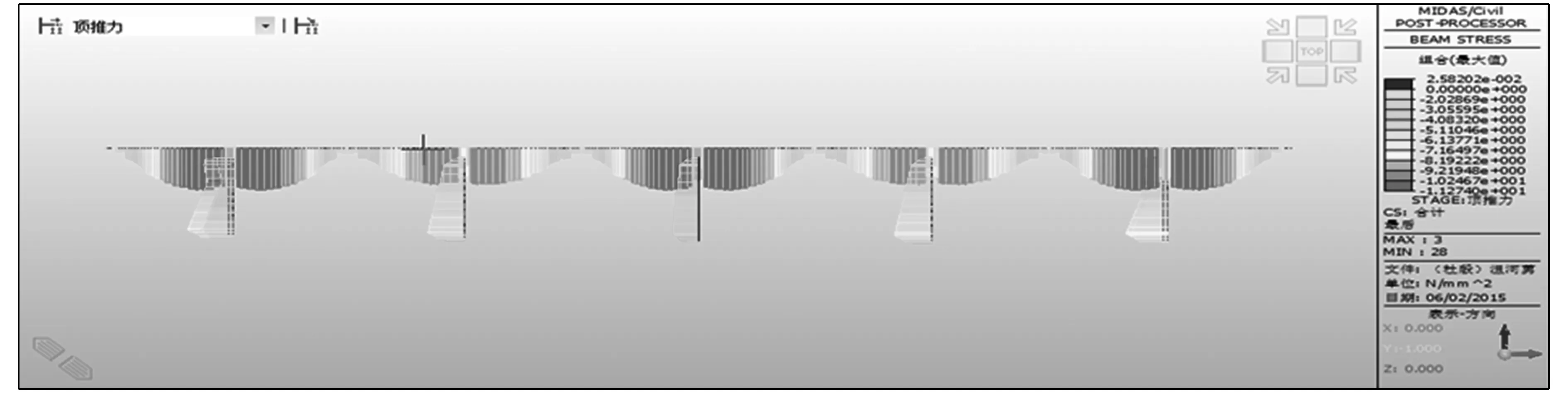
图4 温差为5 ℃时结构应力图Fig.4 Stress diagram of the structure when the temperature difference is 5 ℃

图4中,主梁的最大压应力为11.3 MPa,主墩全截面受压,最大压应力为8.0 MPa.C40、C55混凝土的轴心抗压强度设计值分别为18.4、24.4 MPa.在这2种情况下,施加顶推力时结构主梁、主墩均受压,且没超过设计值,计算的理论顶推力满足工程要求.

当Δt取5 ℃时,在次中跨、中跨分别施加1 000、1 700 kN的顶推力.结构位移计算结果如图5所示.

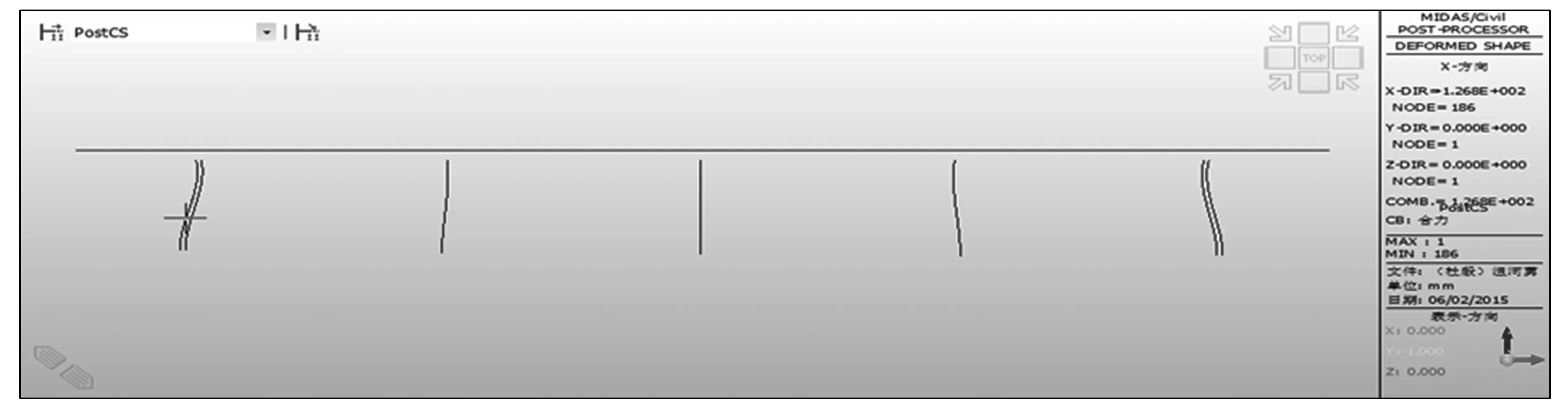
图5 温差为5 ℃时结构位移图Fig.5 Structural displacement diagram when the temperature difference is 5 ℃

图5中,施加顶推力成桥收缩徐变10 a后,13#～17#墩墩顶的水平位移分别为27.0、6.8、2.8、-8.4、-20.5 mm,满足结构要求.

当Δt取10 ℃时,在次中跨、中跨分别施加1 150、1 900 kN的顶推力.结构应力计算结果如图6所示.

图6 温差为10 ℃时结构应力图Fig.6 Stress diagram of the structure when the temperature difference is 10 ℃

图6中,主梁的最大压应力为11.3 MPa,主墩全截面受压,最大压应力为8.7 MPa.施加顶推力时结构主梁、主墩均受压,且没超过设计值,计算的理论顶推力满足工程要求.

当Δt取10 ℃时,在次中跨、中跨分别施加1 150、1 900 kN的顶推力.结构位移计算结果如图7所示.

图7中,施加顶推力成桥收缩徐变10 a后,13#～17#墩墩顶的水平位移分别为14.7 、3.9、-2.8、-5.2、-6.5 mm,满足结构要求.

当Δt取15 ℃时,在次中跨、中跨分别施加1 300、2 100 kN的顶推力,结构应力计算结果如图8所示.

图8中,主梁的最大压应力为11.3 MPa,主墩全截面受压,最大压应力为9.4 MPa.施加顶推力时结构主梁、主墩均受压,且没超过设计值,计算的理论顶推力满足工程要求.

当Δt取15 ℃时,在次中跨、中跨分别施加1 300、2 100 kN的顶推力,结构位移计算结果如图9所示.

图7 温差为10 ℃时结构位移图Fig.7 Structural displacement diagram when the temperature difference is 10 ℃

图8 温差为15 ℃时结构应力图Fig.8 Stress diagram of the structure when the temperature difference is 15 ℃

图9 温差为15 ℃时结构位移图Fig.9 Structural displacement diagram when the temperature difference is 15 ℃

图9中,施加顶推力成桥收缩徐变10 a后,13#～17#墩墩顶的水平位移分别为2.5、0.9、-2.8、-1.9、7.7 mm,满足结构要求.

5 结 论

(1) 本文基于消除墩顶水平位移的思路,考虑了结构体系转换、长期载荷作用下混凝土收缩徐变及实际合龙温度与设计合龙温度的合龙温差等因素,推导了多跨连续刚构桥梁一次性合龙的顶推力理论公式,并进行了工程实例验证,为今后多跨连续刚构桥梁一次性合龙时顶推力的选取提供了参考.

(2) 经计算分析,合龙时顶推力的大小与合龙温差有关,本文给出在温差为5、10、15 ℃合龙时的顶推力推荐值,在温差为5 ℃一次性合龙时,在次中跨、中跨宜分别施加1 000和1 700 kN的顶推力;在温差为10 ℃一次性合龙时,在次中跨、中跨宜分别施加1 150和1 900 kN顶推力;在温差为15 ℃一次性合龙时,在次中跨、中跨宜分别施加1 300和1 900 kN顶推力.

(3) 因仿真分析和结构的实际受力情况存在一定的差异,施工时应以墩顶的水平位移和墩底的拉应力做为目标控制量,顶推力的实际取值应根据结构现场监测的实际情况,在计算的顶推力基础上进行调整.

(4) 本文的计算分析在各墩墩顶同时顶推,同时焊接锁定劲性钢筋骨架工艺的条件下进行.