基于虚拟背景光谱Hausdorff距离的高光谱异常检测及GPU实现

赵春晖, 李佳伟, 闫奕名, 宿 南

(哈尔滨工程大学 信息与通信工程学院, 黑龙江 哈尔滨 150001)

高光谱图像包含丰富的空间与光谱信息,具备对地物精细化处理和分析的能力,借助其特性能够区分地物光谱信息的细微差异[1].因此,目标检测在高光谱图像处理领域具有广泛应用.其中,异常目标检测无需先验信息,更具普适性,成为高光谱目标检测领域的研究热点[2-4].

Reed等提出的恒虚警率RX检测算子[5]被称为异常检测的经典算法.该算法通过求解目标与背景均值向量的马氏距离,构造全局似然比检测算子对高光谱像元逐一进行检测.RX算法需假设背景服从高斯正态分布模型,而实际地物分布是复杂多变的,因此RX检测算法的检测性能受到限制.基于滑动窗模型的局部RX检测器[6-7],通过利用数据的局部背景信息进行检测,与全局信息相比,局部背景信息更能满足假设模型,且可有效检测出局部异常小目标.但是对于背景较为复杂的数据,局部窗口仍难以表征出正态分布,且算法需多次求逆运算,算法的执行效率较低.根据背景信息可以由它的空间邻域信息线性表示,而异常目标不能表示的特点,Li等提出了一种基于协同表示的异常检测(Collaborative-Representation-Based Detector, CRD)算法[8].该算法得到了较好的检测性能,但与RXD算法一样,CRD算法容易受到背景中存在的异常目标和噪声的干扰,从而引起误判.

Hausdorff距离(HD)是一种极大极小距离, 是由非线性关系定义的, 具有非线性特性和有向性, 被广泛应用于模式识别领域[9-11]. 因其能较好地反映地物空间分布特征及不同地物间的明显差别, 近年来也被引进到高光谱图像处理领域. 文献[12]提出基于Hausdorff距离的高光谱图像特征检索方法, 得到了较高的检索准确率. 文献[13]提出的基于改进的Hausdorff距离(MHD)的异常检测算法有效降低了虚警率, 提升了检测性能.

随着成像技术的发展,高光谱数据的空间和光谱分辨率逐渐增大,这为高光谱图像处理的执行效率带来巨大压力.传统算法为了提高效率,利用降维或波段选择等技术去除冗余信息,虽然取得一定效果,但也存在数据信息丢失的弊端.近些年,GPU通用计算能力的壮大,为高光谱图像处理的高效并行实现带来了新思路[14-16]. X.Wu等利用GPU设计改进的PPI混合像元分解算法的并行架构[14],解决了传统算法计算复杂度高引起的耗时问题.A.Paz等提出基于GPU的自动目标检测和分类算法(ATDCA)[15],结合OSP、SAD、SID等多种距离计算方式进行检测,获得了较高的检测和分类效率.根据算法的结构特性,设计适合算法的并行系统架构,可显著提高算法的处理效率.

为了减小背景信息中的噪声及异常点对检测性能的影响,以及高斯背景假设模型对传统算法的束缚,本文提出一种基于虚拟背景光谱Hausdorff距离的高光谱图像异常目标检测算法,记为VBS-HD(Virtual Background Spectral Hausdorff Distance)算法.根据局部空间的相关性,筛选各光谱波段的中间像素代表整个波段的特征,有效去除位于两端的噪声及异常信息,从而虚拟理想化的背景光谱用于异常目标检测.选取Hausdorff度量作为光谱距离测度.由于传感器、天气、大气等因素的影响,数据成像过程中可能会在个别波段中产生孤立噪声点.因此,对待测像元与背景光谱的各波段正反双向距离的计算后,对其进行升序排列,选取前k个结果进行均值化,避免由于孤立噪声点的存在导致结果的错判.最终根据Hausdorff度量判别式实现异常检测.为高效实现海量数据处理过程,本文根据算法结构特点,设计基于GPU/CUDA的并行系统架构,显著提升算法的执行效率.

1 Hausdorff距离相似性度量

光谱相似性测度是指通过一定的度量标准来比较形状间的相似程度.光谱曲线表征了复杂的光谱成像的非线性过程,因此从目标光谱形状的角度探究非线性空间里的光谱差异,可更好地实现非空集合光谱间的距离测度.德国数学家Felix Hausdorff提出的度量准则----Hausdorff距离,很好地考虑了空间目标的形状差异及相对位置差异.Hausdorff距离是一种定义于2个点集间的极大极小距离,描述非空紧集合间的非线性空间几何距离,可更加准确地实现光谱间的相似性度量.

1.1 经典Hausdorff距离

Hausdorff距离(HD)的定义最初是对2组点集相似程度的描述,假设2组集合A={a1,a2,a3,…,am},B={b1,b2,b3,…,bn},则A、B集合间的Hausdorff距离定义为

HD(A,B)=max{h(A,B),h(B,A)} .

(1)

式中,h(A,B)和h(B,A)分别代表点集A和B之间的单向距离,其定义为

‖·‖表示点集A和B之间的距离范数,如Euclidean距离等.两个单向距离具有不对称性,式(2)表示集合A到B的前向距离,即集合A中所有点到集合B的最小距离的最大值,式(3)表示集合A到B的后向距离,即集合B中所有点到集合A的最小距离的最大值.前向与后向距离的较大者构成集合A到B的Hausdorff距离.双向Hausdorff距离表征了两个集合间的最大不相似程度,距离值越小,代表相似程度越高.

从几何角度理解Hausdorff距离[17],可假设集合A和B为2个n维空间中的非空紧致集合,则集合A和B之间的Hausdorff距离可定义为

ρ(A,B)=inf{ε:A⊂B⊕S(ε),B⊂A⊕S(ε)}.

(4)

式中:S(ε)代表半径为ε的封闭球体;⊕表示数学形态学中膨胀操作;ρ为满足一定条件下的最小封闭球体S的半径,条件为A包含在膨胀集合B⊕S(ε)中,B包含在集合A⊕S(ε)中.通过求解集合A的最小膨胀封闭球体半径εA及集合B的最小膨胀封闭球体半径εB,整体Hausdorff度量过程转化为

ρ(A,B)=max{εA,εB}.

(5)

式中,封闭球体半径εA,εB需满足

1.2 改进的Hausdorff距离

Dubuission和Jain匹配被噪声污染的图像时,提出了改进的Hausdorff距离(Modified Hausdorff Distance, MHD)[18].其距离定义为

MHD(A,B)=max{mh(A,B),mh(B,A)}.

(8)

式中,单向距离表示为

(9)

与原始Hausdorff距离相比, MHD测度对存在零均值高斯噪声的图像具有较好的匹配效果, 但由于其对距离值求取均值, 仍然对远离中心的外部点较为敏感,如图1所示. 因而对于目标部分遮挡和存在孤立噪声点的图像, 匹配性能较差.

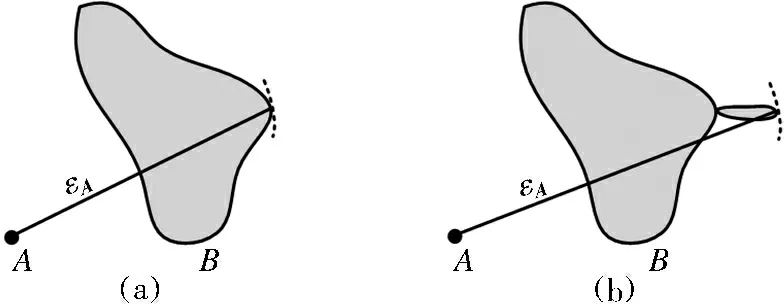
图1外部点对Hausdorff距离的影响
Fig.1 Effect of the external point of Hausdorff distance
(a)—不存在外部点; (b)—存在外部点.

2 VBS-HD异常检测器及GPU实现

2.1 虚拟背景光谱

目前,在高光谱图像处理中,对于异常目标没有明确的定义,普遍认为,一个目标在一定程度上偏离了背景分布,即异常的光谱信息明显不同于背景光谱信息,则称此目标为异常[19].在基于窗口模型的异常检测中,一般通过背景窗口信息均值化表征局部背景信息,用于与待检测像元进行光谱相似性度量.然而,局部背景窗口不能保证全部光谱信息都属于背景信息,若背景窗口信息被较多的异常数据污染时,均值化的结果并不能很好地表征背景信息,因此容易引起误判.

高光谱图像异常目标像元数目远小于背景像元数目,通常,异常光谱的反射率位于背景光谱信息的两端,图2为AVIRIS飞机场数据局部11×11大小区域内,随机选取的10条背景信息与5条异常光谱的光谱反射率分布趋势图.

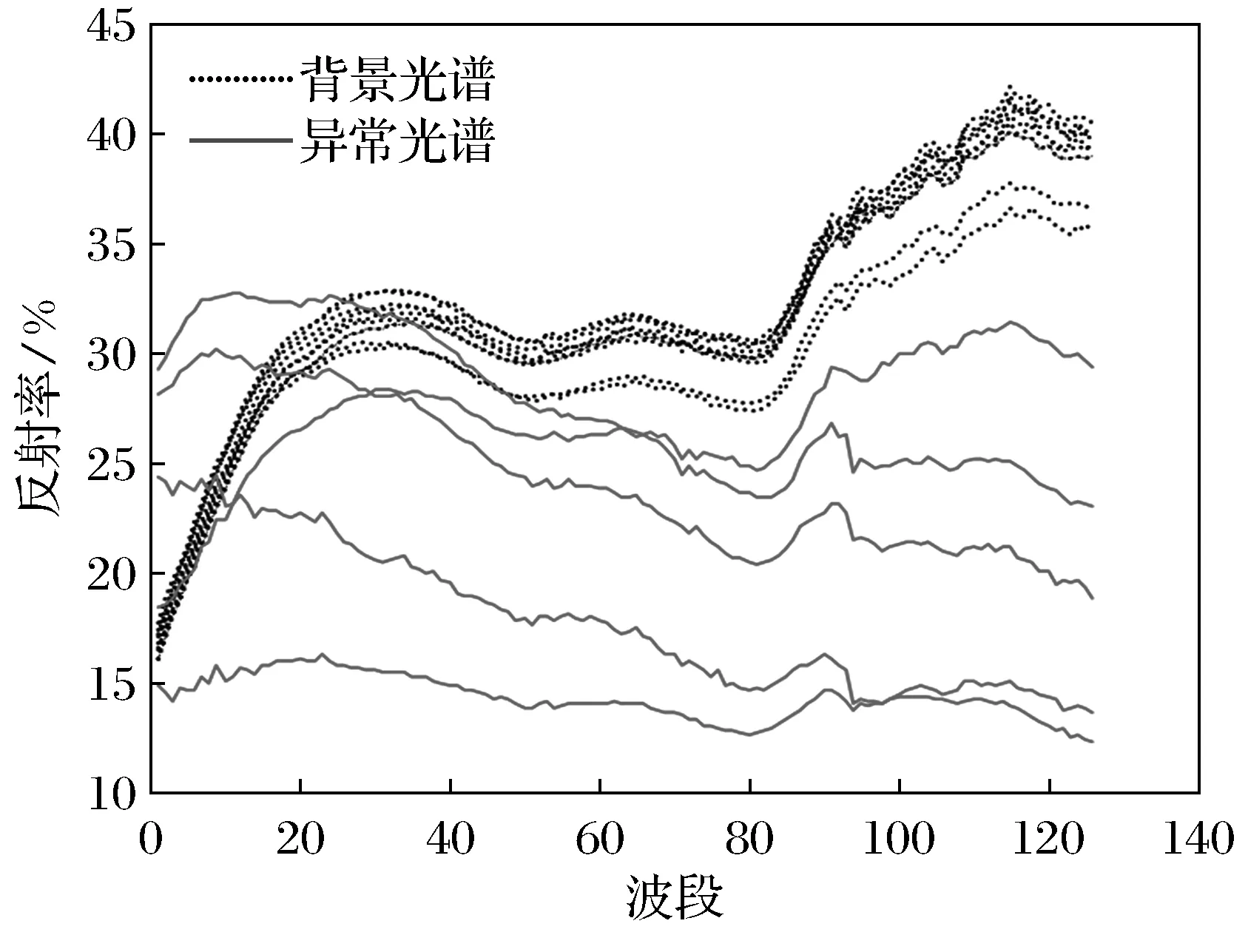
图2 背景与异常光谱分布图Fig.2 Background and anomaly spectral distribution

从图2可看出,异常光谱的反射率明显不同于背景光谱,大多位于背景光谱的两端,因此,可选择各波段的中值来表征局部背景光谱,如式(10)所示.

VB=median{(Dp)L|p∈w2}.

(10)

式中:Dp表示局部区域内的光谱信息;L代表波段数;w2=w×w表示局部窗口大小. 通过选取各波段的中值来构造理想化的虚拟背景光谱, 可更大概率去除背景窗口内的异常及噪声, 有效缓解背景信息混入异常点及噪声对检测结果的影响. 如图3所示, 在异常检测过程中, 利用窗口的中心像素作为待测像元与背景光谱进行比较, 因此,构造虚拟背景光谱时, 应去除局部窗口的中心像元.

图3 检测窗口模型Fig.3 Detection window model

2.2 基于Hausdorff度量的异常检测算子

异常检测算法可分为确定性算法和统计学算法.本文所提出的异常检测算子为确定性算法,通常通过度量背景光谱与待测像元间的距离进行异常检测.这类算法对噪声较为敏感,为了能够更好地去除光谱成像过程中产生的孤立噪声点对检测结果的影响,算法选择改进的部分Hausdorff度量作为距离判别准则.

若集合A的少数元素与集合B的多数元素距离较近,而A中其他元素远离B集合,通过Hausdorff距离的计算,得到的距离将会偏小,而实际上两个集合的相似度并不高.经改进的部分Hausdorff距离很好地解决了上述问题,并有效避免了噪声及远离中心的外部点对距离测度的影响.

该测度需要考虑一个集合中每个元素到另一集合的距离, 并对距离值进行升序排列, 通过阈值k的调节, 采用部分均值的方法得到点到点集间的距离, 以此方式计算两集合的正反双向距离, 通过判别准则最终得到集合间的Hausdorff距离.

假设高光谱图像的待测像元光谱向量表示为A=(a1,a2,…,aL),经式(10)构造的虚拟背景光谱为VB=(b1,b2,…,bL),L为高光谱波段数,则待测像元A中的任意元素ai到背景光谱VB的距离定义为

(11)

式中:b∈VB;j代表ai到b的距离个数.对距离值进行升序排列,选取前k个值进行均值运算,k∈[1,L].则向量A到向量VB的距离定义为

(12)

同样,背景光谱VB到待测像元A的距离定义为

最终,待测像元A与背景光谱VB的Hausdorff度量定义为

HVBS-HD=max{hVBS-HD(A,VB),hVBS-HD(VB,A)}.

(15)

VBS-HD算法的实现步骤如下.

(1) 为了便于高光谱图像边缘信息检测,对原始输入图像进行边缘扩充,扩充大小由局部窗口大小决定.

(2) 对背景窗口内各波段光谱信息进行排序,根据式(10)构造理想化的虚拟背景光谱.

(3) 根据式(11)～式(14),对窗口中心待检测像元与虚拟背景光谱进行正反双向Hausdorff距离度量.

(4) 比较正反双向Hausdorff距离hVBS-HD(A,VB)和hVBS-HD(VB,A),如式(15),选取两距离中最大值作为Hausdorff距离,滑动窗口,重复步骤(2)～(4),实现整幅图像的距离测度,以此衡量各像元的异常程度,得到异常检测灰度结果图.

2.3 VBS-HD算法并行优化模型

随着遥感技术的不断发展,高光谱数据的光谱、空间、时间分辨率都逐渐增大.高光谱图像数据量呈几何级数增长,为高光谱图像处理的执行效率带来了巨大压力.为了提升算法的执行效率,更加适应海量数据的处理需求,充分利用GPU的并行计算能力,设计了VBS-HD算法的并行优化模型.

GPU由内存、缓存及多个流多处理器(Stream Multiprocessors, SM)阵列组成.其中,SM被看作真正的处理单元,每个SM由多个标量处理器核心(Stream Processors, SP)及少量计算单元等构成.NVIDIA推出统一设备架构(Compute Unified Device Architecture,CUDA),为GPU并行计算可编程实现提供了便利.CUDA的软件开发是基于CPU+GPU异构模式的类C语言编程模型.CUDA程序的简易执行过程如图4所示,主机(CPU)端主要负责串行计算及算法流程的控制,设备(GPU)端负责并行任务的计算.把从CPU端传递的并行任务封装成Kernel函数,并根据并行结构配置网格大小,网格由多个线程块(Block)组成,每个线程块包含多个线程(Thread).通过式(16)的索引方式将各任务分配给不同的线程独立运算,实现计算任务多线程并行执行过程.

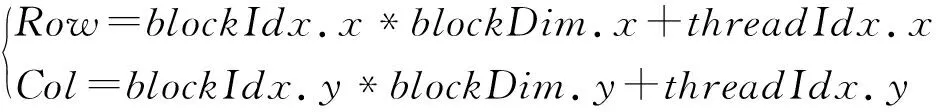
(16)

式中:threadIdx.x和threadIdx.y分别代表线程在其线程块内x和y方向的偏移;blockIdx.x和blockIdx.y分别表示线程在网格内x和y方向的偏移;blockDim.x和blockDim.y代表线程块在网格内x和y方向的坐标维度.

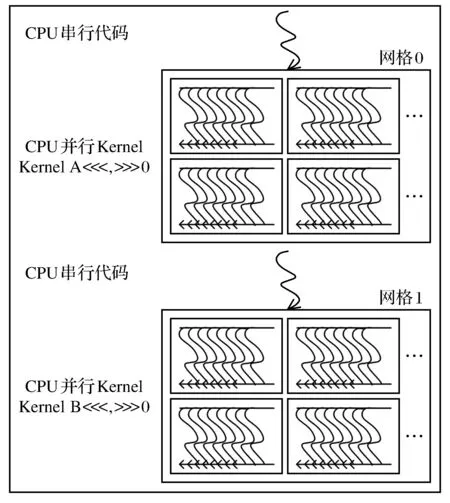
图4 CUDA程序的执行过程Fig.4 The execution process of CUDA program

VBS-HD算法中的数据计算、排序等实现过程相对独立,因此可通过设计合理的并行架构,实现高效执行过程.CPU与GPU之间通过PCI-E总线进行相互通信,其数据带宽制约着并行效率,因此应尽量避免多次的数据传输.为此,在设计的VBS-HD并行架构中,将高光谱数据一次性传输到GPU端,通过相对复杂的指针索引,遍历各窗口元素,以此代替各窗口数据的多次传输过程.GPU内部的存储器占用量及调用过程也会影响并行效果,为了尽量减少不必要的中间变量的存储调用过程,在架构中将整个过程封装在一个Kernel函数内,将中间变量重复利用,省去大部分显存消耗.通过合理的线程调度,实现各窗口独立并行,完成待测像元的异常检测过程.算法并行优化模型如图5所示.

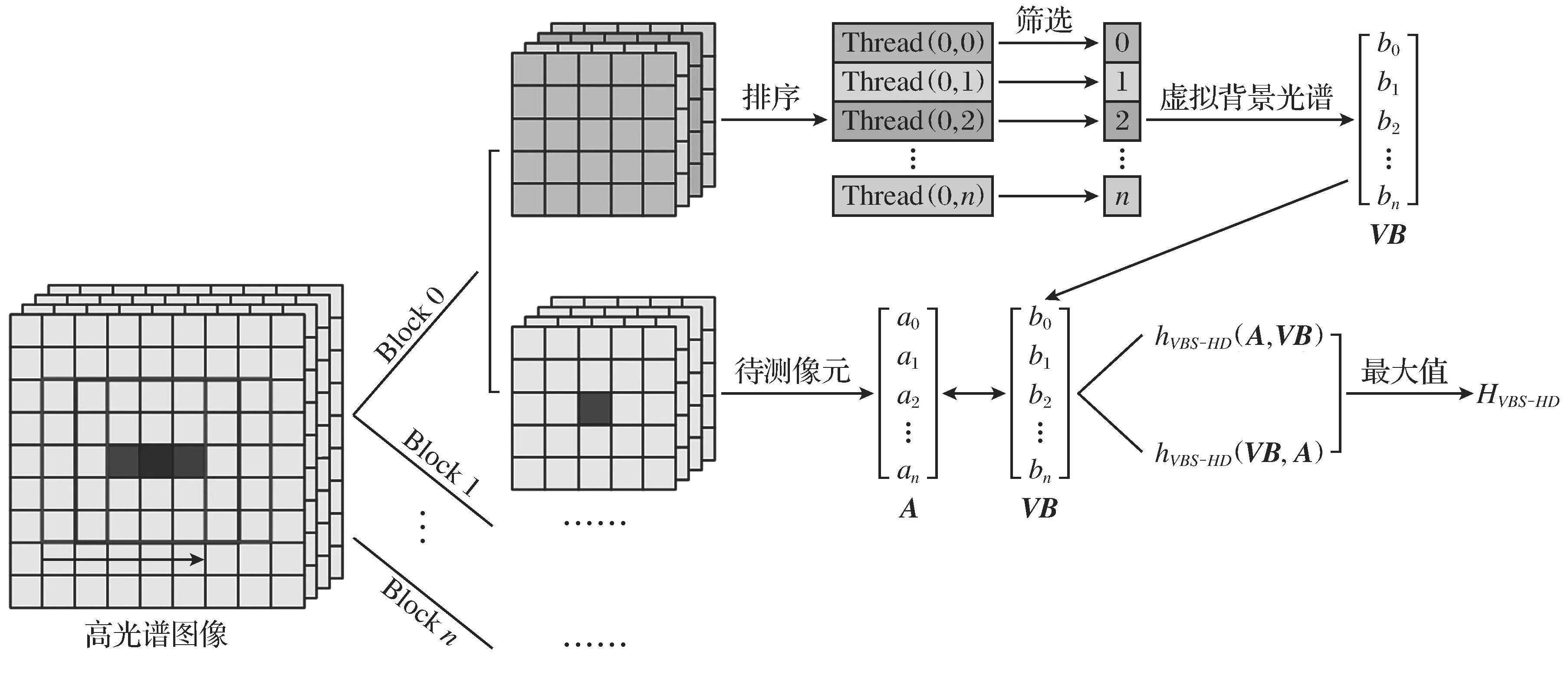
图5 VBS-HD并行优化模型Fig.5 Parallel optimization model of VBS-HD

3 实验分析

为了验证VBS-HD算法的有效性及并行优化后的高效性,分别利用2组真实数据及3组不同大小的模拟数据进行实验仿真操作.实验仿真环境:CPU处理器为Intel Xeon E7-4820,主频为2.0GHz,内存为DDR3 96GB;GPU处理器为NVIDIA Tesla K40m;实验平台为Microsoft Visual Studio 2010集成开发环境.

3.1 数据描述

3.1.1 ROSIS数据

ROSIS数据选自于意大利北部的帕维亚中心图像.该图像由ROSIS光谱仪拍摄,波长范围在0.43～0.86 μm之间,原始图像大小为1 096×715,光谱分辨率为4 nm,空间分辨率为1.3 m.选取115×115的区域用于算法性能分析.背景主要由桥、水波、影子组成,去除水吸收及信噪比较低的波段,剩余102个波段用于实验.图6为ROSIS数据第20波段灰度图像及真实地物分布二值图像.

图6 ROSIS数据Fig.6 ROSIS data(a)—第20波段灰度图像; (b)—真实地物分布图.

3.1.2 AVIRIS数据

AVIRIS数据选自圣地亚哥海军基地图像. 该图像由AVIRIS光谱仪拍摄, 原始图像大小为400×400,224个波段, 波长范围在0.4～1.8 μm之间, 光谱分辨率为10 nm, 空间分辨率为3.5 m. 截取60×60的图像用于检测, 图中的4架飞机作为异常, 去掉水吸收波段及信噪比低的波段后, 剩余126个波段用于实验. 图7为AVIRIS数据第20波段灰度图像及真实地物分布二值图像.

图7 AVIRIS数据Fig.7 AVIRIS data(a)—第20波段图像; (b)—真实地物分布图.

3.1.3 模拟数据

模拟数据的异常目标由AVIRIS数据中多种地物进行插值得到,共4×4=16个异常目标,合成数据大小为128×128,共128个波段.模拟数据的每行目标由同种地物构成.第1列异常目标由纯像元构成,第2列目标由75%目标光谱和25%背景光谱构成,第3列目标包含50%的目标像元光谱特性和50%背景光谱特性.第4列目标包含25%目标像元光谱特性和75%背景光谱特性.图8为模拟数据第20波段灰度图像及目标分布二值图像.

模拟数据用于算法并行性能的分析实验,为充分展现算法的并行特性,在保证密度不变的情况下,将模拟数据扩展成256×256及512×512的图像数据.分别利用3组不同尺寸的模拟图像用于算法的并行优化性能分析,其扩展图像如图9所示.

图8 模拟数据Fig.8 Synthetic data(a)—第20波段灰度图像; (b)—真实地物分布图.

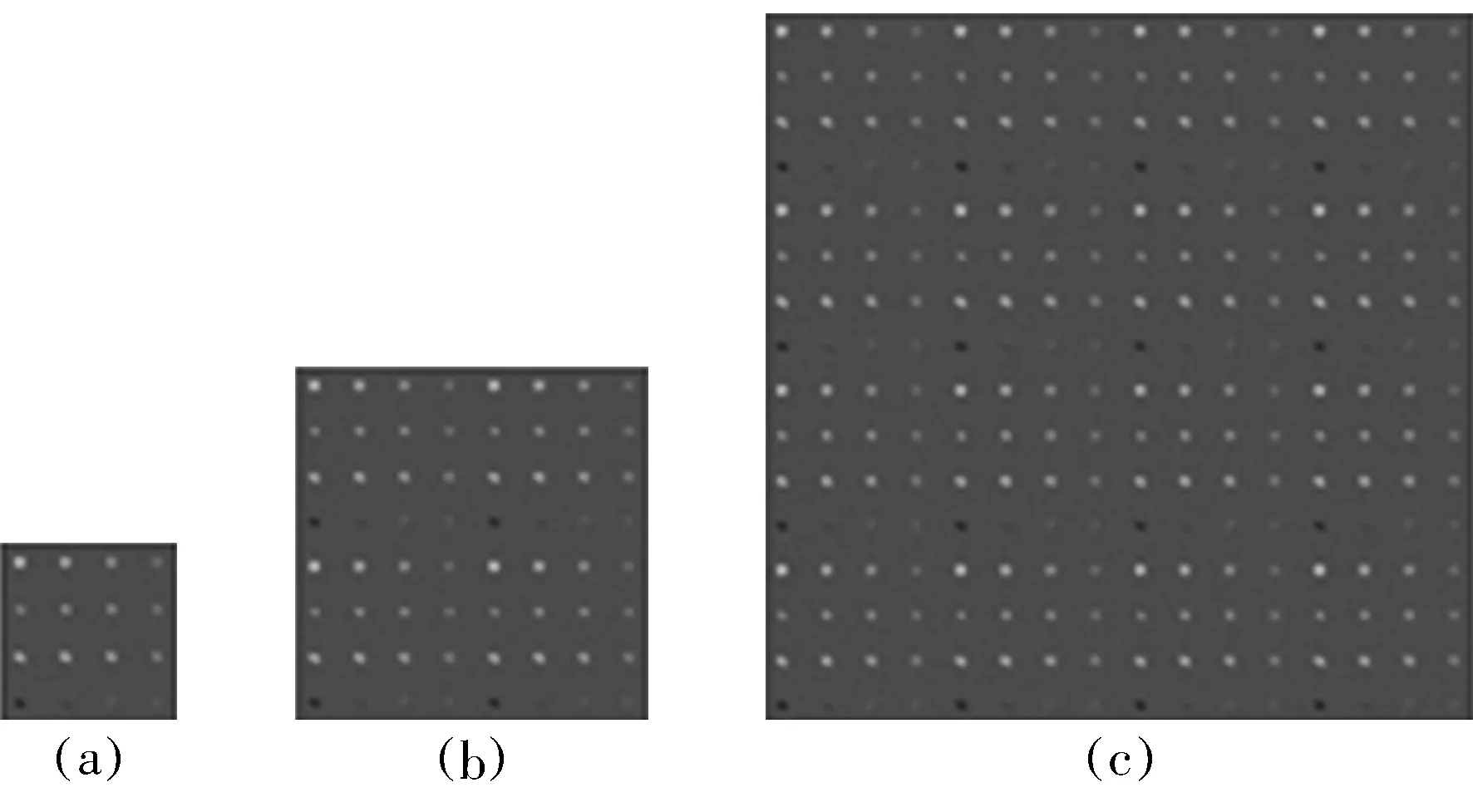
图9 不同尺寸的模拟数据Fig.9 The synthetic data of different size(a)—128×128; (b)—256×256; (c)—512×512.

3.2 参数讨论

3.2.1 参数k对VBS-HD算法的影响

为分析计算部分Hausdorff距离时所选取的前k个距离值对检测结果的影响,利用交叉验证,在ROSIS及AVIRIS数据实验中均选择11×11的窗口大小,进行不同k值情况下的VBS-HD算法检测结果对比实验.

实验结果采用AUC值形式呈现,AUC为接收机操作特性曲线(ROC)的下面积,ROC可以定量分析检测概率与虚警概率间的关系,其曲线下面积可作为检测性能的评判标准,AUC越接近1,则算法的检测性能越好.图10为两组真实数据中不同k值时的检测结果对比图.从图中可以看出,由于ROSIS数据的地物分布相对简单,因此对参数k不敏感,当k为41时,检测性能达到最佳.在AVIRIS数据中,当k值从1升至11时,AUC达到最大值,随着k值继续增大,AUC逐渐降低.

3.2.2 局部窗口w对VBS-HD算法的影响

为分析局部窗口w的大小对VBS-HD算法的影响,通过交叉验证,在ROSIS数据的实验中,选取参数k为41,在AVIRIS数据的实验中,选取参数k为11,在不同窗口大小的情况下进行VBS-HD算法检测结果对比实验.

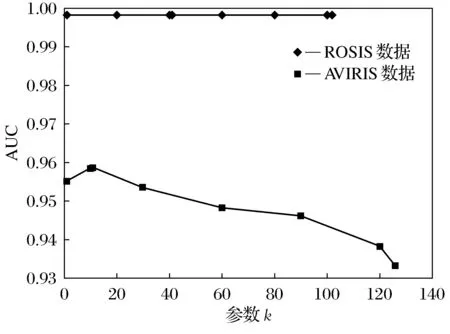
图10 两组真实数据中不同k值的AUC曲线图

如图11所示,对于ROSIS数据,由于地物分布相对简单,局部窗口对其检测性能影响较小,随着局部窗口的变化,AUC值相对稳定,在窗口大小为11×11时,检测结果最佳.在AVIRIS数据中,当窗口从5×5升至11×11过程中,AUC显著增大,而窗口继续增大时,AUC逐渐降低,在窗口大小为11×11时,AUC达到最大值.

3.3 VBS-HD算法的检测性能

选用ROSIS及AVIRIS 2组真实数据进行算法有效性分析.在实验中,将局部RX算法(LRXD)、协同表示的异常检测算法(CRD)、基于改进的Hausdorff距离的异常检测算法(MHD)及背景选取局部均值的基于改进的部分Hausdorff距离的异常检测算法(MLTS-HD)作为对比实验,与VBS-HD算法进行比较,验证算法的有效性.在ROSIS数据实验中,VBS-HD及MLTS-HD选取参数k为41,窗口大小w为11×11;LRXD、CRD及MHD的双窗大小(win,wout)为(3,11).在AVIRIS数据实验中,VBS-HD及MLTS-HD的参数k为11,窗口大小w为11×11;LRXD、CRD及MHD的双窗大小(win,wout)为(5,11).由于CRD对参数λ不敏感[8],因此直接将其设为1.

图12 两组真实数据实验灰度图Fig.12 The gray images of experiment in two real datasets(a)—LRXD; (b)—CRD; (c)—MHD; (d)—MLTS-HD; (e)—VBS-HD; (f)—LRXD; (g)—CRD; (h)—MHD; (i)—MLTS-HD; (j)—VBS-HD.

图12为2组真实数据的检测结果灰度图,由于LRXD需满足背景服从高斯分布,而真实地物很难满足这一特性,因此其检测出异常个数相对较少.与其他4种算法比较,VBS-HD算法检测出的异常目标更加凸显.图13为2组真实数据的检测结果灰度峰度图,其中图13a～图13e是ROSIS数据,图13f～图13j是AVIRS数据.从图中可看出,CRD检测出的个别异常信息值较低,容易湮没在背景噪声中难以区分.与MHD、MLTS-HD相比,VBS-HD算法的抑制背景噪声能力更强,可明显区分背景与异常,能够更好地处理地物较复杂的数据.综合2组结果图,VBS-HD算法具有较高的检测精度,且抑制背景噪声能力较强,使得异常目标更加凸显.

为了更加客观地对各算法的检测性能进行对比,使用接收机特性曲线对异常检测性能进行定量分析,图14所示为2组数据的各算法ROC曲线图.

图14a中,由于ROSIS数据地物相对简单,各算法的检测精度都很高.其中,VBS-HD算法的检测性能最佳,当虚警率为0.004 5时,检测概率达到90%,当虚警率为0.012时,即可检测出全部异常.虽然地物较为简单,但局部背景信息仍难以完全符合高斯分布,因此与其他算法相比,LRXD的检测精度稍低.图14b中,由于MHD算法对数据局部孤立噪声点较为敏感,容易引起误判,因此其检测虚警率较高.虽然在虚警率大于0.18时,CRD的检测概率略高于VBS-HD算法,但整体AUC值仍小于VBS-HD算法,且在虚警率为0.06时,VBS-HD的检测概率就已达到90%.综合来看,VBS-HD算法的检测性能更好.由于VBS-HD算法构造理想化的虚拟背景光谱进行检测,更好地避免了背景信息掺杂异常对检测结果的影响,因此其检测性能好于MLTS-HD算法.综上所述,VBS-HD算法具有较高的检测性能,且抗噪声干扰能力较强,抑制背景噪声能力较好,可适用范围更广.

3.4 VBS-HD并行优化算法的高效性

由于真实高光谱图像数据量很大,为后续的数据处理效率带来很大压力.因此,为了进一步提升算法的执行效率,充分利用GPU的并行计算能力,挖掘VBS-HD算法的并行特性,在GPU/CUDA模型下,设计算法的并行系统架构.为验证并行算法的高效性,利用图9所示的3组不同尺寸的模拟数据进行实验,实现并行VBS-HD算法与CPU串行版本的VBS-HD算法执行效率对比验证.表1为VBS-HD算法的并行与串行版本执行效率对比情况.

为了去除计算机的脉冲误差,表1中的检测时间均为10次实验后的均值.由表1可看出,基于GPU的并行算法执行时间明显低于CPU串行版本.由于算法需进行多次排序等过程,随着数据量的增大,排序、筛选等过程的次数也逐渐增多,因此算法的执行时间将明显增大,但与CPU串行版本相比,GPU并行算法的执行时间随数据量增大而增加的趋势较为缓慢,其增加的时间多数源于GPU与CPU间的数据传输.由表1加速比数据可看出,在模拟数据为128×128时,加速比为6.101倍,模拟数据增大到512×512时,加速比为13.952倍.随着数据量的增大,GPU的加速效果更加凸显,GPU的并行机制适合海量数据的处理,因此基于GPU/CUDA模型下的并行算法可有效缓解高光谱数据量大带来的数据处理压力,更加满足实际应用需求.

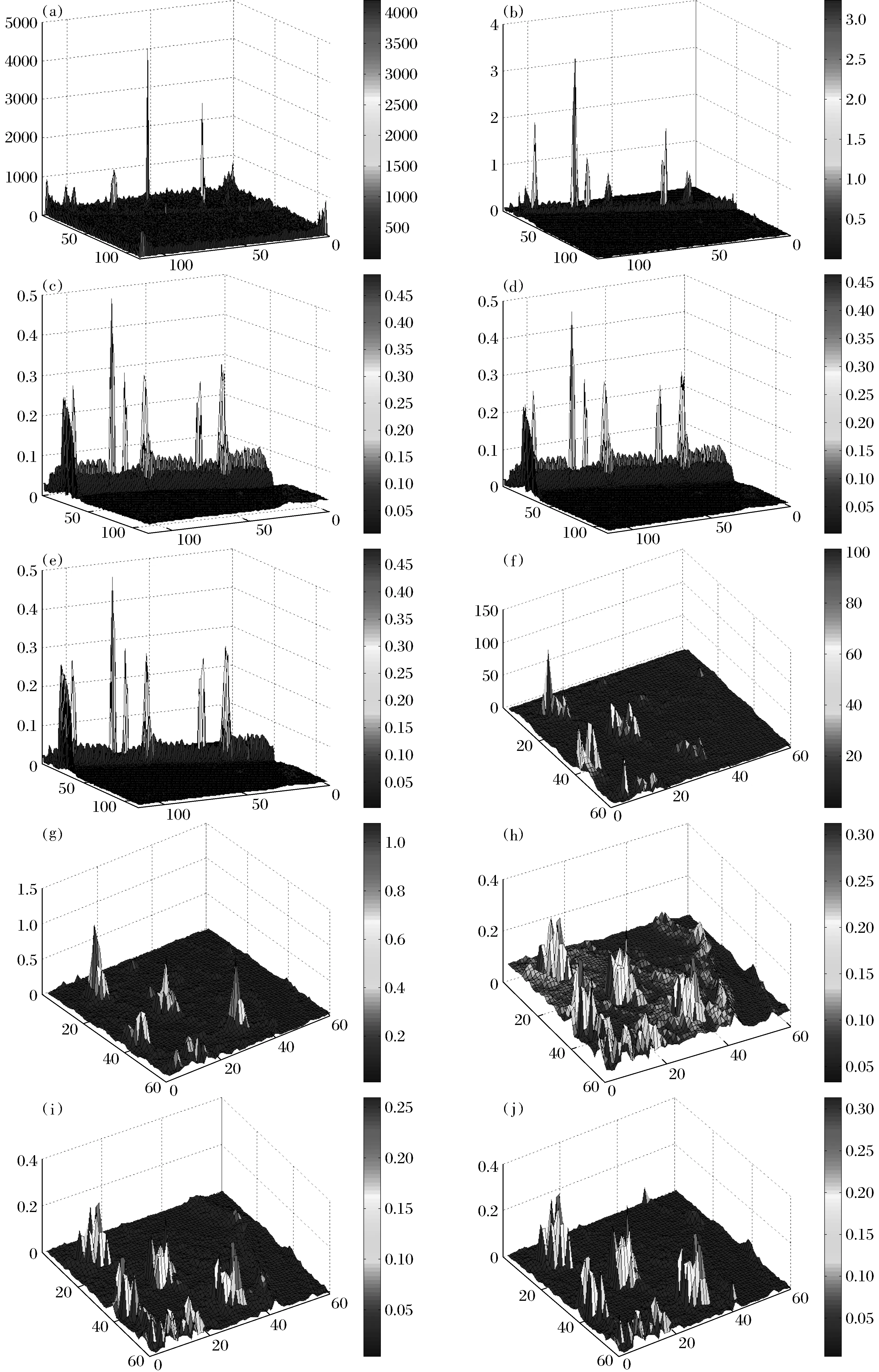
图13 两组真实数据实验灰度峰度图Fig.13 The gray kurtosis figures of experiment in two real datasets(a)—LRXD; (b)—CRD; (c)—MHD; (d)—MLTS-HD; (e)—VBS-HD; (f)—LRXD; (g)—CRD; (h)—MHD; (i)—MLTS-HD; (j)—VBS-HD.

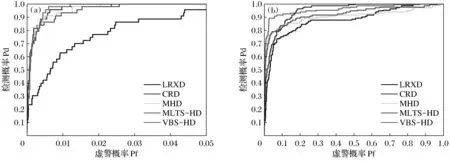
图14 两组真实数据接收机操作特性(ROC)曲线

模拟数据总处理时间/sCPUGPU加速比128×128195.67132.0746.101256×256476.58048.2579.876512×512964.45869.12613.952

4 结 论

本文提出一种高光谱图像异常目标检测算法(VBS-HD),该算法通过在空间邻域内构造理想化虚拟背景光谱,有效缓解因背景信息掺杂异常对检测结果的影响.同时利用改进的部分Hausdorff度量作为光谱相似性度量准则,从Hausdorff距离所定义的非线性角度衡量光谱间的关系,可更加准确地对像元属性进行划分,且通过选取前k个距离值均值化,避免由孤立噪声点引起的误判.为了提升算法执行效率,充分利用GPU的并行特性,设计算法的并行优化模型.实验证明,VBS-HD具有较高的检测精度,且抗噪声干扰能力较强,其并行优化模型显著提升了算法的执行效率,且随着数据量的增大,加速效果更加凸显,进一步满足实际应用中海量数据的高效实现需求.