基于身份及RSA的简短代理环签名方法

赵艳红, 陈晓玲

(安徽财经大学 管理科学与工程学院, 安徽 蚌埠 233000)

随着网络及信息技术的快速发展,信息安全问题尤为重要,基于身份代理的环签名方案在计算机、电子商务等方面具有很高的研究及应用价值[1-2].1996年,Mambo[3]提出代理签名的概念.在代理签名方案中,原始签名者将消息签名的签名权委托给代理签名人.这种签名支持为分布式网络中的客户提供服务,以避免对单个服务器的依赖.2003年,Zhang[4]等人设计了基于双线性对的代理盲签名和代理环签名方案,这是代理环签名概念的首次提出.2004年,为了方便代理环签名的公钥证书管理,Cheng[5]等人首次提出了基于身份的代理环签名,使用签名者的身份而不是公钥和证书.2005年,Lu[6]等人构造了具有消息恢复的指定验证者代理签名方案.2006年,Huang[7]等人在无随机预言机的基础上设计了代理签名方案.2007年,Liu[8]等人设计了保护代理签名安全的方案对抗未被授权的代理签名的攻击.2008年,Schuldt[9]等人提出的基于身份的代理环签名方案解决代理密钥暴露攻击,在以往的方案中,如果代理签名者的暂时密钥被泄露,它们的长期密钥将受到损害.2011年,Shim[10]等人提出指定验证者的短代理签名方案.2012年,Chou[11]等人提出匿名的代理签名方案.2014年,Asaar[12]提出基于身份的代理环签名方案的定义和安全模型,并提出了可证明安全的无双线性对的基于身份的代理环签名方案,证明了在随机预言机模型下,基于RSA假设是安全的.由于高概率破坏方案的不可伪造性,导致解决RSA带来的安全问题的概率太小.2015年,张瑞丽[13]等人基于双线性对运算和离散对数的困难性问题,提出了基于身份的代理签名.2016年,景东亚[14]提出了指定验证者代理签名方案.

本文提出了基于身份及RSA的简短代理环签名方法.在随机预言模型下,基于RSA的方法被证明是安全的.本文提出的方法是不基于双线性对的基于身份的简短代理环签名方法,并且由于该方法的安全性方面与代理环中的成员数无关,在安全方面有优势,比现有的基于身份的代理环签名方法具有更高的效率.

1 预备知识

1.1 符号说明

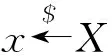
(3) 设#是空字符串,|x|是x的比特长度,θ←C(x1,…)代表算法C输入x1,…,输出到θ.

(4) 如果算法A是(t,qg,qp,qe,qd,qprs,ε)有界的,即算法的运行时间最多为t,使得最多在时间qg查询随机预言机G,在时间qp查询随机预言机P,在时间qe查询Extract,在时间qd查询ProxyDelegation和在时间qs查询Sign预言机,可以至少以ε的概率赢得游戏.

1.2 RSA假设

RSA密钥生成器KGrsa是生成三元组(N,e,d)的算法,这样N是两个大素数p和q的乘积,且ed=1 modφ(N),其中φ(N)=(p-1)(q-1).算法B打破KGrsa和RSA单向性的有利条件定义为

1.3 签名方法的安全模型相关定义

基于身份的代理环签名必须满足2个独立的安全性:代理签名者身份的不可伪造性和隐私.实现存在性不可伪造对抗适应性选择消息,对基于身份的代理环签名方法选择身份攻击,在Yu[15]等人的文中提到3种类型的潜在敌手:A1、A2、A3.

如果基于身份的代理环签名方法对2型或3型敌手是安全的,那么它对1型敌手也是安全的.对A1、A2、A3敌手的不可伪造性,在挑战者C和敌手A之间开始以下游戏.

(1) Setup: 挑战者C运行ParaGen算法,用安全参数l获得系统参数para和主密钥(mpk,msk),然后发送(mpk,para)给A.

(2) KeyExtract查询:A可以要求密钥对应于每个身份IDu,然后运行KeyExtract算法,C返回私钥xu给敌手.

(3) DelegationGen查询:敌手A可以基于消息空间描述符w上原始签名者的身份IDo和身份集ID请求授权,ID的选择是具有身份IDo的原始签名者将其在w上的签名权授权给具有身份集ID的委托代理.对此,C运行KeyExtract算法得到原始签名者的密钥xo,并返回σo←DelegationGen(Para,mpk,IDo,ID,w,xo).

此外,敌手A为信息空间描述符w和代理签名者的身份集ID提供了一个具有身份IDo的原始签名者的授权σo.这个授权是从DelegationGen算法得到或被敌手A产生.

对于A=A1,

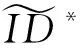
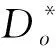
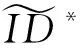
存在性不可伪造的攻击敌手A1[12]的正式定义如下.

定义1 如果没有有界的(t,qg,qe,qd,qs,ε)敌手A赢得游戏,基于身份的代理环签名(t,qg,qe,qd,qs,ε)存在不可伪造性抵抗自适应性选择消息(权证)和选择身份攻击.

对于A=A2,

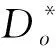
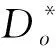
存在性不可伪造的攻击敌手A2[12]的正式定义如下.

定义2 如果没有有界的(t,qg,qe,qd,ε)敌手A赢得游戏,基于身份的代理环签名(t,qg,qe,qd,ε)存在不可伪造性抵抗自适应性选择消息(权证)和选择身份攻击.

对于A=A3,

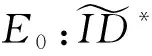
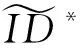
存在性不可伪造的攻击敌手A3[12]的正式定义如下:

定义3 如果没有有界的(t,qg,qe,qs,ε)敌手A赢得游戏,基于身份的代理环签名(t,qg,qe,qs,ε)存在不可伪造性抵抗自适应性选择消息(权证)和选择身份攻击.

2 基于身份及RSA的简短代理环签名方法

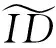
(1) Generation:输入是系统安全参数l,输出是系统参数Para,系统主密钥(msk,mpk),即(Para, (msk,mpk))←ParaGen(l).

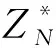
(2) Extract:输入Para,mpk,主密钥msk=d和用户身份的IDu,输出身份IDu相应的密钥(密钥分配中心计算xu=G(IDu)dmodN,并将安全且经过身份验证的通道上的用户密钥xu发送给身份为IDu的用户),即xu←Extract(Para,mpk,msk,IDu).

(3) ProxyDelegation:如果具有身份IDo的原始签名者愿意将其签名权委托给具有身份集ID的委托代理,该算法被采用.输入是Para,mpk,IDo,ID的原始签名者的密钥xo和信息空间描述符w⊆{0, 1},输出是一个授权σo,即σo←ProxyDelegation(Para,mpk,IDo,ID,xo).

(4) VerifyDelegation:输入是Para,IDo,ID,w和σo,如果σo是一个有效的授权,输出是1,否则为0,即{0, 1}←VerifyDelegation(Para,mpk,IDo,ID,w,xo).

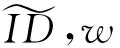
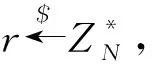
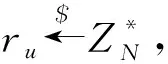
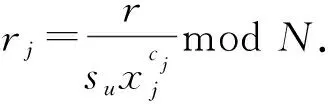
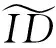
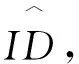
① 如果m∈w,检查;否则,停止;

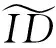
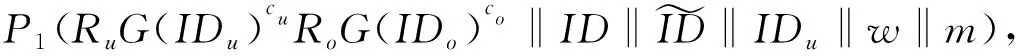
3 方法分析

3.1 方法的安全性分析

本文验证了该方法的正确性,并证明了代理签名者的身份隐私和在随机预言模型下该方法存在不可伪造性.如果基于身份的代理环签名方法对2型(3型)敌手是安全的,那么它对1型敌手也确保安全.为了证明所提出的方法的不可伪造性,需要证明它是不可伪造的敌手A2、A3.

首先,验证所提出的方法的正确性,所有的计算都做了模n,但是为简单起见忽略了这点.

在下文中将需要以下分裂引理.

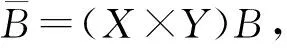
(1)Pr[B]≥α;

(2) ∀(x,y)∈B,Pry′∈Y[(x,y)∈A]≥δ-α;

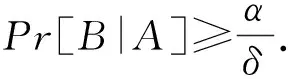
定理1 所提出的方法对敌手A2是(t,qG,qPo,qd,ε)安全的,如果RSA函数与KGrsa的关联是(t′,ε′)单向的,并且

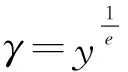
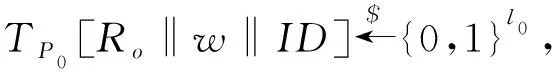
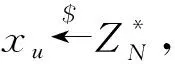
(3) 基于IDu的Extract查询:算法B查找T[IDu]=(b,xu,Xu),如果这项尚未定义,它执行查询G(IDu).如果b=0,则B返回xu;否则,设置badPE←true,中止A2执行.

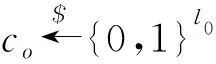
因此,B不中止签名仿真的概率至少是η≥βqE-qd(2qd+qP0)2-lN.

由于P0是随机预言机,c0=P0(Ro‖w‖ID)事件发生的概率小于2-l0,除非在攻击期间被询问.因此,接下来在成功攻击期间,很可能查询(Ro‖w‖ID).对预言机P0查询后生成有效伪造概率的下界是ε2≥ε1-2-l0.然后,B使用预言机重放技术[18]解决RSA问题.

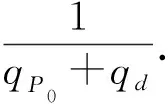
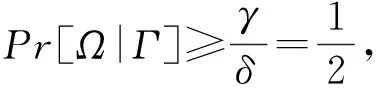
算法B的运行时间t′是A2的2倍,加上响应Hash查询所需的时间,qEExtract和qdProxyDelegation查询的时间.假设ZN中1(多)次模指数运算需要te时间,当所有其他操作需要时间为零,由于每个随机预言机G或Extract查询需要的时间最多为1次指数运算,1个授权模拟需要2次指数运算,B的运行时间为t′≤2(t+(qG+qE+2qd)te).证明完成.

定理2 所提出的方法对敌手A3是(t,qG,qP,qE,qprs,ε)安全的,如果与Kgrsa相关的RSA函数是(t′,ε′)单向的,并且

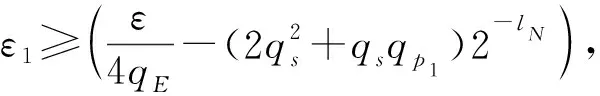
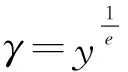
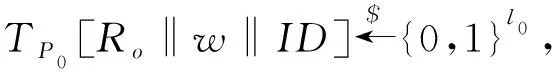
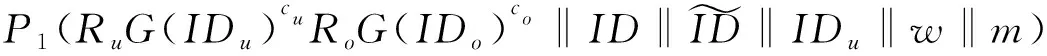
(4) 基于IDu的Extract查询:算法B查找T[IDu]=(b,xu,Xu),如果未定义此项,则执行查询G(IDu).如果b=0,则B返回xu;否则,设置badPE←true,中止A3的执行.

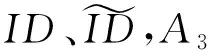
证明 类似要求1的证明.

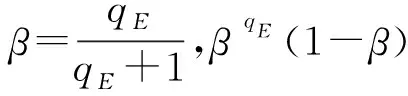
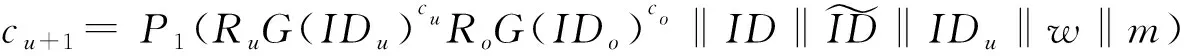
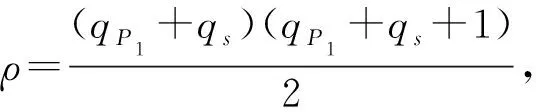
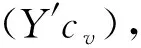
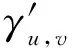
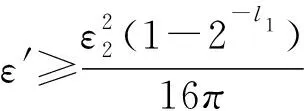
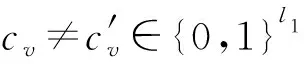
算法B的运行时间t′是A3的两倍,包括t加上响应Hash查询、qEExtract查询和qsSign查询所需的时间.假设在ZN中,当所有其他操作时间都为零,1次(多次)指数运算所需时间是te,由于每个随机预言机G或Extract查询需要最多1次指数运算,1次Sign模拟需要(2z+1)指数运算,B的运行时间是t′≤2(t+qG+qE+(2z+1)qs)te.证明完毕.

证明 区分器D自适应分配随机预言机、Extract、ProxyDelegation和Sign的多项式的次数,如定理1和2的证明.

3.2 方法的实现及效率分析

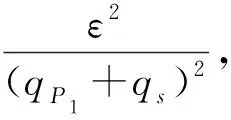
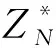
表1 本文提出方法与文献[12]签名方法比较Table 1 Comparison of the proposed scheme with the signature scheme in reference [12]

如表1所示,本文提出的签名方法与文献[12]中提出的签名方法相比,在签名长度上有优势.由于l1≪|ZN|,签名长度由因子|ZN|-l1改进.本文所提出方法密钥和签名长度缩减,提高了运行效率.

4 结 语

本文从RSA假设出发,提出了一个可证明安全的基于身份的简短代理环签名方法,在随机预言机模型中证明它是安全的.与RSA算法相比,该方法的安全性得到了改善,因为它与代理环中代理签名者的数量无关.本文提出的方法没有使用双线性对,避免了配对计算,所以提出的方法使运算复杂度降低,提高了运行效率,在效率上有适当的优势.信息时代,在计算机及网络应用广泛的情况下,黑客入侵、恶意软件泛滥、违法监控、隐私泄露事件常有发生,本文提出的签名方法具有不可伪造性及安全性,不受代理密钥暴露攻击的影响,抗攻击性强,具有广泛的应用前景,可解决电子商务、云计算等领域中存在的安全问题.