基于尺度自适应与增量式学习的人脸对齐方法

陈 平，龚 勋

(西南交通大学 信息科学与技术学院，成都 611756)(*通信作者电子邮箱xgong@swjtu.edu.cn)

0 引言

人脸对齐是在给定的人脸图像上自动精确定位人脸特征点，如瞳孔、嘴角、鼻尖等。人脸对齐的应用很广泛，比如人脸识别、表情识别以及人脸动画自动合成等。人脸对齐大致可以分成三个子问题：1)对人脸表观图像建模；2)对人脸形状建模；3)建立人脸表观图像与人脸形状的关联。基于模型的人脸对齐研究也围绕着这三个方面开展：基于统计学习的主动形状模型(Active Shape Model, ASM)[1]提出利用点分布模型表示人脸形状信息，并结合主成分分析(Principal Component Analysis, PCA)[2]进行降维，建立了可以通过加权表示人脸形状变分段化的形状模型。主动外观模型(Active Appearance Model, AAM)[3]方法考虑如何建模整张人脸的表观信息，此方法是在ASM模型的基础上建立形状模型和纹理模型，并将两个模型进行有机的结合。局部约束模型(Constrained Local Model, CLM)[4]方法分别继承了ASM的高效性和AAM的准确性，使得人脸对齐效果得到了进一步提升。随着人脸对齐技术的发展，基于级联形状回归模型级联姿态回归(Cascaded Pose Regression, CPR)被Dollr等[5]在2010年首次提出，并用于人脸形状的预测。接着，具有鲁棒性的级联姿态回归(Robust Cascaded Pose Regression, RCPR)[6]在实现特征点定位的同时，还可以对特征点的可见性进行判断。

近些年来，监督下降方法(Supervised Descent Method，SDM)[7]从考虑如何使用监督梯度下降的方法来求解非线性最小二乘问题，推动了人脸对齐在现实工程中的应用。SDM认为相同特征点位置之间的尺度不变特征变换(Scale-Invariant Feature Transform, SIFT)[8]特征应该相似，从而利用牛顿法建立级联回归模型，在人脸上取得较好的定位效果。接着，Ren等[9]用随机森林模型学习局部二值特征(Local Binary Feature, LBF)；刘袁缘等[10]提出非约束人脸特征点精确定位；张海艳等[11]提出应用姿态估计的人脸特征点定位方法；贾项南等[12]提出改进的显式形状回归定位算法。除了基于回归的人脸对齐方法，基于深度学习的方法也大放光彩，如多任务级联卷积网络(Multi-Task Cascaded Convolutional Network, MTCNN)[13]，实现了高精度的人脸检测和特征点定位。

以上这些基于级联回归人脸对齐训练过程中都要对原始图片数据进行尺度变换的处理。一方面，图片的变换会导致纹理的损失和形状的微调，会影响到特征的准确提取；另一方面，坐标尺度选择不适合，会直接影响人脸对齐的精度。同时，当发现已有模型的泛化能力不够时，通常的解决办法是把新的数据集加入到原来的数据集中，重新训练模型。这样直接丢掉原有模型，不仅否定了自己以前的实验结果，而且重新训练带来的训练时长、模型不收敛等问题，甚至在面对庞大的数据集时，回归求解根本不可计算。针对这些问题，本文提出一种基于增量式学习(Incremental Learning, IL)和尺度自适应的人脸对齐方法：在增量式学习方面，通过充分利用原模型的预测结果与真实值带来的偏差，按照一定的学习率增加原模型的参数值，快速有效地提高原模型的泛化能力。在人脸尺度自适应方面，利用在人脸框内投影而来的初始人脸与标准人脸建立对应的映射关系，在迭代求解时，把任意尺度的人脸特征点映射归一到标准尺度，实现人脸尺度的自适应；在特征提取时，计算当前预测特征点在原始图片的位置，实现特征在原图上的提取。实验结果表明，本文所提方法有效地解决了已有模型泛化能力不够就要被丢弃的尴尬，并且可以大幅度提升人脸的对齐精度。

本文主要工作如下。

1)利用不同人脸框的初始特征点与标准人脸特征点建立映射关系，将不同尺度的人脸统一到标准尺度，避免了图片归一化带来的纹理损失，同时分析不同尺度下对模型预测的影响，并给出了最佳的人脸尺度。

2)提出一种增量式学习的回归训练方法。该方法在原有模型的基础上，在新的数据集上进行训练，避免了丢弃原模型和全部重新训练带来的模型训练时间长、不收敛甚至不可计算等问题，能够快速、有效地提高原模型的泛化能力。

1 人脸特征点与特征的关系建立

在人脸图像中，特征点是描述人脸形状的重要信息，特征描述子是根据特征点在图像位置提取而来。优秀的特征描述子具有人脸尺度、缩放、光照等不变性，因此不同人脸相同特征点位置的特征描述整体上应该相似。图1显示不同人脸在鼻尖处的特征直方图。

如图1所示，根据特征直方图可以看出不同人在相同位置提取出来的特征在整体上是相似的，因此推导出特征与特征点的关系函数：

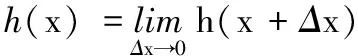
(1)

其中：x为当前预测特征点(人脸形状)，h(x)表示从x处提取特征的函数，当Δx趋近0的时候，相同位置的特征值相同，因此引入一个关系函数r(t)消除特征与特征点的量纲：Δx=h(x)(r(t))，令R=r(t)，建立特征与特征点偏移量间的最小化目标函数：

(2)

其中x*代表人脸的手工标注点。式(2)通过不断最小化Δx使得预测特征点的坐标逼近手工标注点的坐标。由于这个方程式非二次的，不可能一步迭代完成。为了进行线性回归，令Φ=h(x)，建立线性回归方程：

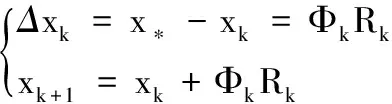
(3)

其中：k代表第k次迭代，根据式(3)可以利用特征Φ来进行特征点位置的预测。

图1 不同人脸的相同位置有相似特征

但是进行算法训练时，为了统一人脸尺度对原始图片进行归一化处理，导致特征不能在原图上进行准确提取，因此，如何在统一人脸尺度的同时实现特征在原图上的提取是一个值得研究的问题。

2 尺度自适应与增量式学习对齐算法

为了在方法训练时，在保证人脸尺度统一的同时也能在原图上进行特征提取，本文提出一种任意尺度的人脸自动投影到标准尺度人脸的方法，简称人脸投影变换(Face Projection Transformation， FPT)。该方法巧妙地避开了图片预处理阶段，通过建立任意人脸与标准尺度人脸的特征点映射关系，实现人脸尺度的自适应和原图纹理的无损失。同时本文提出了一种基于增量式学习训练方法：在原有模型的基础上，在新的数据集上进行训练，这样避免了丢弃原模型和全部重新训练带来的模型训练时间长、不收敛甚至不可计算等问题，能够快速、有效地提高原模型的泛化能力。

2.1 FPT

FPT方法的核心是将任意尺度的人脸自动投影到标准尺度人脸。在实现人脸尺度自适应时，为了探究尺度对人脸对齐的影响，分别选择100×100、200×200、400×400、600×600这4种不同的尺度人脸。对于每种尺度，选取多张带有手工标注点的相同尺度正脸图片，对标注点集进行对齐，采用Procrustes Analysis[14]算法，得到该尺寸下的标准人脸，如图2所示。

选取一个标准人脸，对于任意尺度人脸的特征点坐标进行投影变换。假定人脸的一个特征点为p=[uv1]T，对应的标准人脸的特征点为pstd=[u′v′ 1]T，根据平面投影变换可以得到：

T[uv1]T=[u′v′ 1]T

(4)

(5)

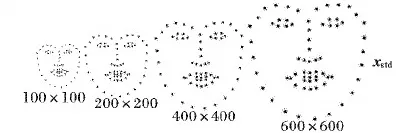
图2 不同标准人脸的尺度

根据式(5)得到任意尺度人脸与标准尺度人脸间的变换矩阵T，建立任意尺度人脸在标准尺度人脸下的表示，如式(6)：

x′=FPT(x)=Tx

(6)

其特征点在标准尺度人脸下的形象表示如图3所示。

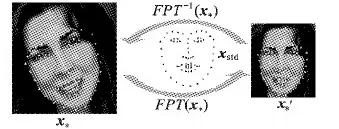
图3 FPT坐标变换

从图3可以看出，原始人脸的特征点在经过FPT后，不仅在坐标尺度和标准人脸xstd的坐标尺度一致，而且在形状上逼近了标准人脸xstd。

2.2 基于FPT的人脸自适应对齐

本文将FPT应用到人脸对齐，简称人脸投影变换对齐(Face Projection Transformation Alignment， FPTA)。在训练阶段，选择标准尺度下的人脸xstd，引入FPT方法。令x*′=FPT(x*)，xk′=FPT(xk)，根据式(3)得到FPTA的线性回归方程：

(7)

其中：xk+1=FPT-1(xk+1′)；Φk为当前预测的特征点在原图提取出来的特征；R为特征与偏移量间的关系矩阵，该关系矩阵的最优化求解函数如下：

(8)

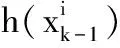
算法1 FPTA算法。

2)用式(5)建立脸特征点x*在标准人脸xstd下的映射关系及其表现形式x*′；

3)利用xk在原图上进行特征提取；

4)利用式(8)求得对应的Rk和xk+1′；

5)利用xk+1=FPT-1(xk+1′)求出特征点在原图的位置；

6)重复步骤3)～5)直到达到指定次数K。

通过实验仿真发现，当K≥4时算法收敛。

从图4看出，FPTA算法在计算Δx时利用FPT方法实现人脸尺度的自适应，在迭代更新的时候利用FPT逆运算得到预测特征点在原图的位置，从而实现特征在原图上的提取。通过实验仿真发现，当迭代次数达到4时算法收敛。

图4 人脸对齐实例

2.3 基于增量式学习的FPTA人脸对齐

通过式(8)可以看出，当模型泛化能力不够时，只能把新的数据集加入到原有数据集中，重新训练，以得到满足要求的新模型；但是数据量的增大会直接导致模型训练时间增加与不收敛，甚至当数据集过大的时候，求解时，庞大的矩阵将会出现不可计算等问题，因此在FPTA算法的模型基础上，进行增量式学习(IL)训练：

(9)

其中：lr是微调系数，称为学习率，初始由人工设定。式(9)可以通过最小二乘法解决ΔRk，进行模型的微调：

(10)

通过式(10)的求解可以很快让原模型在新的数据集上进行多次微调，从而到达对新姿态也有较好泛化能力的模型。本文将此方法简称为增量式学习的FPTA算法，具体描述如算法2。

算法2 基于增量式学习的FPTA算法。

1)fork=1 toKdo

2)对于每张图片利用Rk和式(7)进行特征点xk′的估计；

3)利用式(10)计算ΔRk，并求出Rk′；

4)利用式(9)和Rk′评估出xk+1′；

5)利用xk+1=FPT-1(xk+1′)反解算出特征点在原图的位置。

通过实验发现，有时在新数据集上进行一次模型的微调并不能达到模型对该数据集的泛化要求时，可以设置较小的学习率对模型进行多次微调。

3 实验结果与分析

本章通过5个实验来说明本文的主要工作与贡献。所有实验都是Intel i5- 7500 CPU@3.40 GHz的Windows 10平台下进行的，实验选取的数据集如表1。

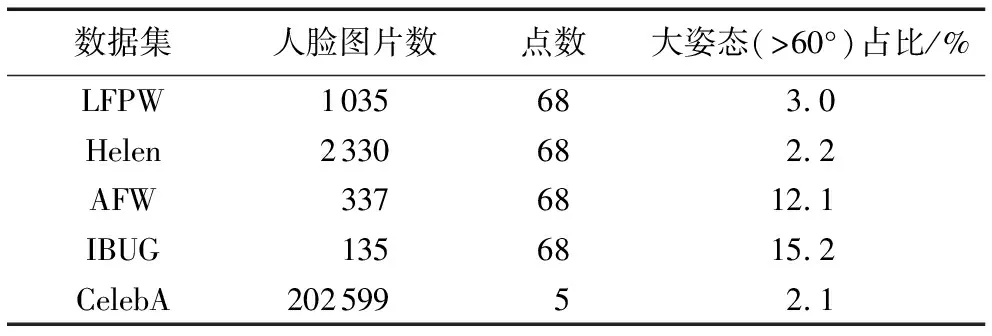
表1 实验用人脸数据集

其中LFPW(Labeled Face Parts in the Wild)包含811张训练图片和224张测试图片；Helen有2 000张训练图片和330张测试图片；AFW和IBUG具有大姿态的人脸；CelebA(CelebFaces Attributes)包含20多万名人的大规模人脸数据集，其图像涵盖大姿态、复杂的背景，非常适合用于算法鲁棒性的检测。

同时，实验特征提取可以使用SIFT、方向梯度直方图(Histogram of Oriented Gradient, HOG)[15]等特征，本文从速度考虑，实验选用HOG特征。在求解最小二乘优化时可以使用卷积神经网络(Convolutional Neural Network, CNN)进行求解。实验发现当迭代次数K=4时，算法收敛效果较好。

3.1 人脸归一化尺度选择

为了快速研究不同归一化尺度对人脸对齐算法影响，本节分别选择尺度为100×100、200×200、400×400和600×600的标准人脸，用FPTA算法在LFPW训练集上进行训练，单次训练迭代4次用时1.5 h，并在Helen、AFW、LFPW上进行测试分析。测试的分析结果如表2所示。

表2 不同标准人脸下的FPTA结果 %

根据表2的结果可以分析出，坐标尺度在400×400时对齐精度最好。通过实验数据分析发现，当选取的尺度过小时，人脸框与标准人脸产生的初始人脸特征点集存在更多的重合，会导致模型泛化能力减弱；当尺度过大的时候，初始人脸特征点集尺度离散较大，导致求解最小二乘时，模型的参数数值差过大，从而影响到模型的鲁棒性，所以在后面的实验中都选择400×400的标准人脸。

3.2 基于增量式学习的FPTA与同类算法比较

本节共有两个实验，第1个实验是把LFPW、Helen、IBUG结合为一个数据集(共2 946张)进行单独的FPTA训练，得到了modelA；第2个实验是先在LFPW、Helen训练集上进行FPTA算法的训练集，得到初始modelB，考虑到modelB对大姿态人脸没有较好的泛化能力，所以利用增量式学习在IBUG(135张)上进行模型的微调，得到对大姿态有较好泛化能力的modelC，并对modelA、modelB、modelC进行了实验分析。三个模型的对齐误差分析结果如表3。

表3增量式学习的对齐平均误差分析

%

Tab. 3 Alignment average error analysis of incremental learning

%

通过表3分析可以看出，通过增量式学习得到的modelC比modelB具有更好的泛化能力，而且其泛化能力比直接利用全部数据集训练得到modelA的要更强一些；并且modelC的训练时间比modelA的更短。同时在保证实验环境相同的前提下，用开源的LBF算法和集成回归树(Ensemble of Regression Trees, ERT)[16]算法在Helen、AFW、LFPW测试集上进行68个特征点的对齐误差测试分析，分析结果如表4所示。

表4 68个特征点的平均误差比较 %

根据表4分析得出，本文方法在3个数据集上表现最好，对齐误差都在4%以下。特别是在姿态变化较大的AFW数据集上，本文方法的对齐精度比ERT高2个百分点，比LBF高4个百分点，这充分说明了增量式学习的优势。图4为本文方法的一些定位实例，从图中看出，本文方法对姿态、遮挡有很好的鲁棒性。

3.3 鲁棒性测试

算法的鲁棒性是评价算法好坏的标准，鲁棒性分析是在对齐误差的基础上进行进一步的分析，因此，本节在3.2节的实验基础上选取了68个特征点中的15个关键点(每个眼睛边缘6个点、鼻尖1个、2个嘴角)和基于深度学习的MTCNN、由粗到精的自编码网络(Coarse-to-Fine Auto-encoder Networks， CFAN)[17]和深度神经网络(Deep Convolutional Neural Network, DCNN)[18]进行5个关键点(两个瞳孔、两个嘴角、一个鼻尖)的对齐误差分析。其中每个瞳孔的坐标由每个眼睛边缘的6个点平均得来。MTCNN和DCNN是目前基于深度学习的最主流的人脸对齐方法，CFAN是人脸识别框架Seetaface中的人脸对齐方法。对齐误差如图5所示。

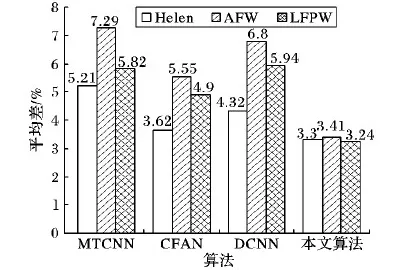
图5 对齐误差分析

通过图5可以知道，在本文算法的对齐误差都稳定在0.03左右，MTCNN、CFAN和DCNN波动相对较大。汇总各数据集的测试结果后，FPTA的平均对齐精度比MTCNN高了2.79个百分点，比CFAN高了1.37个百分点，比DCNN高了2.37个百分点。在对齐误差的基础上，本文采用标准差对算法进行鲁棒性分析，图6为本文算法与基于深度学习的算法的分析结果。

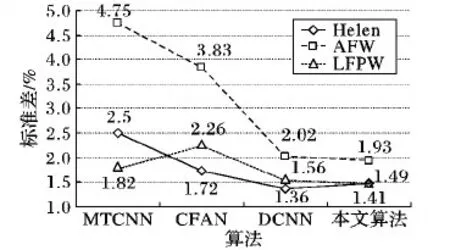
图6 不同算法的鲁棒性分析

从图6可以看出，基于深度学习的算法的标准差在AFW上都最大，且大于2%，但是本文算法的标准差还是在2%以下。结合其他两个数据集的结果，本文算法的鲁棒性比MTCNN高了1.39个百分点，比CFAN高了0.97个百分点，与DCNN近似，因此本文算法在68个点的训练模型中选取出来的5个特征点在小数据集上无论在对齐精度上还是算法的鲁棒性上都要优于目前基于深度学习的人脸对齐算法。

为了进一步测试算法鲁棒性，本文在大数据集上作人脸的5个关键点测试。为了缩短大数据集的测试时间，本实验利用按照3.2节的第2个实验选取7个点(两个嘴角、四个眼角、一个鼻尖)进行增量式学习模型训练。在测试的时候把两个眼角的平均坐标作为该眼的瞳孔坐标。同时，在相同实验环境下，对开源的MTCNN和CFAN也作了相应的测试，与本文方法的对比分析如表5所示。

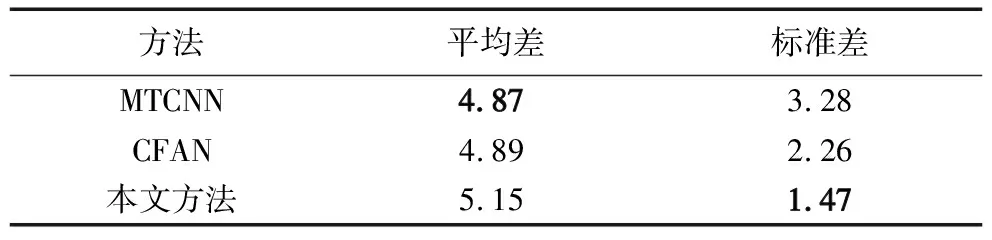
表5 大数据集上5个特征点的比较 %

本实验中，CelebA是标准化后的数据集，有202 599张，去掉人脸框检测错误带来定位误差比较大的人脸后，MTCNN、CFAN和本算法测试了相同的人脸一共181 509张。从表5结果可以看出，本文算法对齐精度略低于基于深度学习的对齐算法；但是从标准差来看，本文算法具有更强的鲁棒性。图7显示的是对齐误差较大的样例，实验发现，当样本姿态较大时，对齐误差相对较大。这是因为训练样本的大姿态占比较少，导致算法模型对大姿态人脸没有较好的泛化能力。

图7 CelebA中错误大的样本

4 结语

本文从不同人脸相同特征点位置的特征描述子大致相似出发，建立特征与特征点偏移量的关系方程，并提出一种基于尺度自适应与增量式学习的人脸对齐方法：通过利用人脸框生成初始预测点与标准的人脸点建立映射关系，实现纹理特征在原图上的提取和人脸尺度的归一化；接着建立增量式学习方程，利用已有的模型在新的数据集上进行增量式的学习，快速有效地增强了原模型的泛化能力。实验证明：本文的人脸尺度的选择与增量式学习的方式，在人脸对齐上取得了很好的效果；同时该方法不仅适用于人脸对齐，还适用于其他回归模型的求解。