高斯消元译码下LT码性能分析
2018-08-27索龙龙张更新边东明谢智东
索龙龙,张更新,边东明,谢智东,田 湘
(1.解放军陆军工程大学 通信工程学院,南京210007; 2.南京邮电大学 通信与信息工程学院,南京210003)(*通信作者电子邮箱bian_dm@163.com)
0 引言
通信,核心问题就是保证信息能够准确无误且高效地从信源发送到目的节点,因而数据的可靠传输策略备受关注。
在空间通信环境下,星地间信道由于受到远距离、天气变化及遮挡等因素的影响,数据传输时延长且丢包率较高,使得地面成熟的传输控制协议(Transmission Control Protocol, TCP)中端到端确认重发机制性能急剧下降[1-4],尤其是在多用户量的广播系统。例如,当一个系统有很多用户时,高的丢包率会导致系统在较短时间内接收到大量的数据重传请求,降低系统的传输性能。与此同时,空间系统长的传输时延以及大量数据重传的共同作用将使得全部数据包成功可靠传输的时延变长,往往使得用户无法忍受。

LT码通常采用两种译码算法:置信传播(Belief Propagation, BP)[11-12]以及高斯消元(Gaussian Elimination, GE)[13-14]。其中BP算法译码复杂度低,但成功译码所需的编码数据包较多;与BP相反,GE算法译码所需码字冗余较少,但复杂度略高。随着时代发展的进步,GE算法逐步得到很大程度的应用,一方面是硬件水平的提高,使得算法复杂度已经不再成为主要矛盾;另一方面是对实时性要求较高的应用,例如话音、流媒体等,要求采用短码字、译码冗余少以保证成功传输所需的时延尽可能地短。
尽管高斯消元算法得到了比较广泛的研究与应用,但针对高斯消元算法下LT码字性能的理论分析仍然不尽完善。文献[15-16]也只是给出了十分宽松的上、下界,而且计算表达式十分复杂,并不能很好地指导实践应用以及实际过程中的码字优化设计。
针对文献[15-16]提出的LT码性能分析方法计算复杂且准确度不高这一问题,本文从高斯消元译码算法的本质出发,对LT码的性能展开研究分析,给出了基于概率转移的性能计算表达式以及一种简单有效的性能衡量指标。
1 LT码
为克服传统差错控制策略的不足,Luby等[7]于2002年提出来第一种实用的数字喷泉码编码方案——LT码。LT码是一种随机编码,没有固定码率,可以由原始的数据包产生任意数量的编码数据包。
1.1 LT码编码算法

步骤1 根据LT码预先设计的度的概率分布{Ω1,Ω2,…,Ωk},随机采样得到一个度值d(1≤d≤k)。
步骤2 均匀随机选择d个不同的原始数据包。
步骤3 选取的d个不同的原始数据包进行异或编码生成编码包,选取的d个原始数据包称作该编码包的邻居。
重复以上步骤就可以源源不断地产生任意数量的编码数据包。若记k个原始数据包为x=[x1,x2,…,xk],n个编码数据包为y=[y1,y2,…,yn],则编码算法又可以写成矩阵形式:
y=xGk×n
(1)
其中Gk×n为码字的生成矩阵[8,17]。
1.2 LT码高斯消元译码算法
高斯消元译码,也被称作最大似然的译码,主要步骤如下。
步骤1 判断生成矩阵Gk×n是否可逆,如果是,则可以进行译码;如果不是,则译码停止。
步骤2 如果Gk×n可逆,将生成矩阵Gk×n和编码包y组成的分块矩阵[Gk×n,y]变换为[I,x],则x部分即为译出的原始数据包。
高斯消元算法主要思想是求解线性方程组,若生成矩阵Gk×n可逆,则可成功译码。其数学思想即求解方程:
(2)
2 传统LT码性能界分析
高斯消元译码算法能否成功译码取决于生成矩阵Gk×n是否可逆,可逆则译码成功;否则译码失败。而Gk×n是否可逆,可以通过计算Gk×n的秩rank(Gk×n)进行判断,则可以得到以下结论:
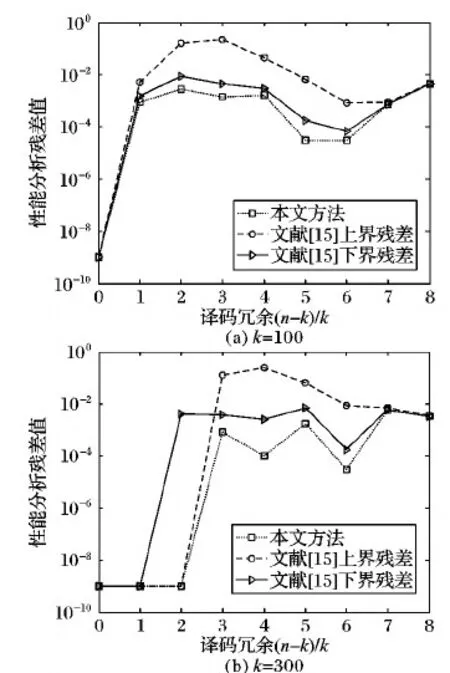
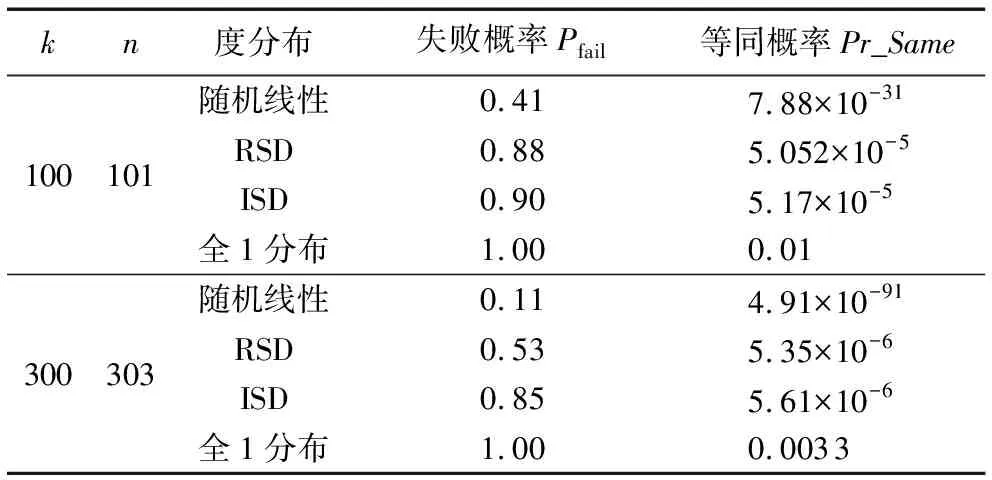
1)若n 2)若n≥k,则存在可能rank(Gk×n)=k,若rank(Gk×n)=k,则Gk×n可逆,译码成功。 文献[15-16]给出了LT码在高斯消元算法下译码失败概率的上、下界。 结论1 对于LT码LT(Ω(x),k,n),若记编码冗余为γ=n-k,任意一个原始数据包译码失败的概率为Pb,则: (3) (4) 证明 见参考文献[15-16],这里不再赘述。 为表述方便,记PbMIN≤Pb≤PbMAX。 若记译码失败的概率Pfail,则有: Pfail=1-(1-Pb)k (5) 由此,很容易得到结论2。 结论2 1-(1-PbMIN)k≤Pfail≤1-(1-PbMAX)k。 证明 根据式(5)以及边界关系,很容易得到结论2,这里不作赘述。 因为式(5)不涉及循环计算,其计算复杂度为O(1),因而文献[15-16]提出的性能分析方法复杂度主要由式(3)、(4)决定。 式(3)计算Pb上界时有三层循环求和运算,由内及外的求和运算分别是s=0,2,…,2⎣d/2」,d=1,2,…,k,w=1,2,…,k,因而由加法带来的运算次数是O(k3),与此同时,式(5)还存在组合运算与幂运算,其中组合运算复杂度为O(k),幂运算复杂度为O(n),因此式(3)的计算复杂度为O(nk4)。 式(4)计算Pb下界时只有一层循环求和运算和幂运算,其中求和运算复杂度为O(k),幂运算复杂度为O(n),因而式(4)的计算复杂度为O(nk)。 传统方法虽然给出了LT码字在高斯消元算法下性能的上、下界,但是存在着不足与缺陷:一是性能界十分宽松,并不能很好地指导实践应用;二是计算表达式十分复杂,无法利用到实际过程中的码字优化设计当中。基于上述考虑,本文基于译码过程中编码数据包与生成矩阵秩之间的必然联系,给出了基于概率转移的LT码性能分析方法。 高斯消元译码算法其能否成功译码取决于生成矩阵的秩是否为满秩,译码器接收到一个编码数据包就会使得原有生成矩阵秩发生变化,秩加1或保持不变。基于此,本文提出基于概率转移的LT码性能分析方法,表述如下。 对于LT码字LT(Ω(x),k,n),译码失败概率为n个编码数据包时所有生成矩阵Gk×n秩小于k概率的和,若记Pr(n,r)为n个编码数据包时生成矩阵Gk×n秩为r的概率,则有译码失败概率Pfail: (6) 全1度分布是LT码字最简单的形式,也是LT码字最基本的样式。 定义1 全1度分布函数Ω(x)如式(6)所示: Ω(x)=x (7) 即: (8) 为分析全1度分布码字性能,本文给出定理1。 定理1 对于全1度分布有: (9) 证明 当有1个编码数据包,生成矩阵Gk×1为k×1的,则Pr(1,1)=1; 当m 当m≥r>1时,由于1个编码数据包,只能使得生成矩阵多1列,生成矩阵的秩就只能保持不变或加1,因而 Pr(m,r)=Pr(m-1,r)·Pr{(m,r)|(m-1,r)}+ Pr(m-1,r-1)·Pr{(m,r)|(m-1,r-1)} (10) 其中:Pr{(m,r)|(m-1,r)}为条件概率,表示m-1个编码数据包时生成矩阵秩为r条件下m个编码数据包时生成矩阵秩为r;Pr{(m,r)|(m-1,r-1)}为条件概率,表示m-1个编码数据包时生成矩阵秩为r-1条件下m个编码数据包时生成矩阵秩为r。 由于每次生成的编码数据包度均为1,即生成矩阵的每一列的权重为1,因而有且只有当新的列与所有其他列不同时,会使得原有生成矩阵的秩增加,即: Pr{(m,r)|(m-1,r)}=r/k (11) Pr{(m,r)|(m-1,r-1)}=(k-r+1)/k (12) 联立式(9)~(11),定理1得证。 联立式(6)、(9),即可计算获得全1度分布码字精确的译码失败概率。 式(6)只含有一层循环加法运算,因而复杂度为O(k);利用式(9)计算Pr(n,r)为迭代运算,需要迭代计算所有Pr(nn≤n,rr≤r≤k),由于每次迭代不涉及循环计算(复杂度为O(1)),因而式(9)计算Pr(n,r)的复杂度为O(nk),则全1度分布码字精确的译码失败概率Pfail计算复杂度为O(nk2)。 随机线性码字指的是生成矩阵中元素0、1均为等概出现,也代表着每一个编码数据包也是等概率出现。 定义2 随机线性码度分布函数如式(13)所示: (13) 即: (14) 与全1度分布类似,随机线性码性能分析如下。 定理2 对于随机线性码有: (15) 证明 其中Pr(1,1)=1,以及当m 当m≥r>1时,同理有: Pr(m,r)=Pr(m-1,r)·Pr{(m,r)|(m-1,r)}+ Pr(m-1,r-1)·Pr{(m,r)|(m-1,r-1)} (16) k个原始数据包,生成向量共有2k-1种(所有组合共2k个,生成向量必须除掉全0向量),根据矩阵秩的定义,当生成矩阵的秩为r时,2k-1种生成向量中,其中2r-1种能够由生成矩阵的列线性生成,剩余2k-2r种则不能由生成矩阵的列线性生成,而随机线性码每种生成向量的产生概率相同,则有: Pr{(m,r)|(m-1,r)}=(2r-1)/(2k-1) (17) Pr{(m,r)|(m-1,r-1)}=(2k-2r)/(2k-1) (18) 联立式(16)~(18),定理2得证。 联立式(6)、(15),即可计算获得随机线性码精确的译码失败概率。 与全1度分布类似,随机线性码的译码失败概率Pfail计算复杂度主要由式(6)、(15)决定。其中式(6)只含有一层循环加法运算,因而复杂度为O(k);利用式(15)计算Pr(n,r)为迭代运算,需要迭代计算所有Pr(nn≤n,rr≤r≤k),与全1度分布不同的是,每次迭代包含幂运算(复杂度为O(k)),因而式(15)计算Pr(n,r)的复杂度为O(nk2),则全1度分布码字精确的译码失败概率Pfail计算复杂度为O(nk3)。 对于一般性LT码,度分布的不均匀性会使得不同生成向量的产生概率不同,生成矩阵Gk×m与Gk×(m+1)之间秩的变化十分复杂且不具有规律性,因此很难像全1度分布以及随机线性码那样,通过计算生成矩阵秩的变化来获得精确的译码失败概率。为解决一般性码字性能衡量的难题,本文给出了一种新的指标参数——等同概率Pr_Same。 定义3 等同概率Pr_Same是指LT码LT(Ω(x),k,n)任意产生两个相同编码数据包(等同于两个相同生成向量)的概率。 根据定义,结合高斯译码原理(生成矩阵Gk×n可逆),可以得到结论3。 结论3Pr_Same越大,码字译码失败概率Pfail越大;反之Pr_Same越小,Pfail越小。 证明Pr_Same越大,则生成矩阵Gk×n中任意两列相同的概率越大,Gk×n中相同列的数目越大,Gk×n可逆的概率越小,则码字译码失败概率Pfail越大;反之亦然。 定理3给出了Pr_Same的计算表达式。 定理3 对于LT码LT(Ω(x),k,n) (19) 证明 任意两个编码数据包相同意味着:1)两者的度相同;2)度的连接关系一致,即编码数据包的邻居相同。 等同概率Pr_Same计算复杂度主要由式(19)决定。式(19)只涉及一层循环加法运算以及组合运算,因而其复杂度为O(k2)。 本文分别对全1度分布、随机线性码以及一般性LT码的性能衡量方法进行了仿真验证,其中全1度分布、随机线性码与文献[15-16]的方法作了比较,一般性LT码采用了经典的鲁棒孤波分布(Robust Soliton Distribution, RSD)以及理想孤波分布(Ideal Soliton Distribution, ISD)。值得说明的是:每个数据包大小为20 bit,译码失败概率通过500次Monte-Carlo仿真计算所得;对于任意码字LT(Ω(x),k,n),仿真图、表中采用的译码冗余为(n-k)/k。 图1给出了对于全1度分布LT码,基于概率转移方法与文献[15-16]的方法对码字性能评价的对比曲线。结果表明,基于概率转移方法可以精确表征码字的译码失败概率,性能分析最大残差降低到0.004 3。与之对比,文献[15-16]方法给出了性能曲线的上下界,但是上、下界曲线比较宽松,性能分析最大残差为0.215 7,无法准确衡量码字译码性能。 图2给出了对于随机线性码字,基于概率转移方法与文献[15-16]的方法对码字性能评价的对比曲线。结果表明,基于概率转移方法依然可以精确表征码字的译码失败概率,性能分析最大残差降低到0.012 4;但是此刻传统方法给出的性能的上、下界曲线,都比较宽松,性能分析最大残差为0.893 2,无法准确衡量码字译码性能。 结合图1~2结果可知,文献[15-16]方法尽管给出了码字性能的上、下界,但是无法准确衡量码字性能;相反,基于概率转移方法能够准确计算全1度分布LT码、随机线性LT码的性能。 为证明等同概率Pr_Same与译码失败概率Pfail间的正比关系,文章仿真了不同类型LT码字(具体参数如表1所示)的译码概率Pfail,对比计算了等同概率Pr_Same。 图1 全1度分布LT码性能分析曲线 图2 随机线性LT码性能分析 Tab. 1 Simulation parameters 表2分别给出了原始数据包个数为100、300时,等同概率Pr_Same与译码失败概率Pfail间的对应关系。表2结果表明,随着等同概率Pr_Same的递增,译码失败概率Pfail也随之上升,即一定程度上表明两者存在正比关系。同时也说明等同概率可以作为一个衡量LT码性能的指标,等同概率越小,译码失败概率越小,码字性能越好。 表2 译码失败概率Pfail与等同概率Pr_Same对应关系 本文对LT的性能进行了理论分析,推导了准确计算全1分布以及随机线性LT码性能的数学表达式;同时,针对一般码字的复杂情况,给出了一种性能评价指标体系——等同概率。理论分析以及仿真结果表明,相比已有方法,提出的新的性能计算方法准确度高,评价指标体系简单有效。本文的局限性在于一般性码字性能的准确衡量还有待进一步研究。下一步工作主要可以从两方面展开:一是进一步研究码字性能的准确衡量;二是立足于现有结论可以对码字的优化设计展开研究。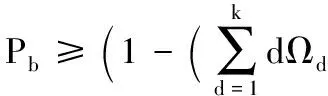
3 基于概率转移的LT码性能分析
3.1 基于概率转移的LT码性能分析
3.2 全1度分布码字性能分析

3.3 随机线性码字性能分析
3.4 一般性LT码字性能分析
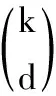
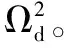

4 仿真验证


5 结语
