树索引数据差分隐私预算分配方法
2018-08-27汪小寒韩慧慧张泽培俞庆英郑孝遥
汪小寒,韩慧慧,张泽培,俞庆英,郑孝遥
(1.安徽师范大学 计算机与信息学院,安徽 芜湖 241003; 2.安徽师范大学 网络与信息安全安徽省重点实验室,安徽 芜湖 241003)(*通信作者电子邮箱hanxiaoahnu@sina.com)
0 引言
在移动通信时代,人们的医疗、支付、购物、导航等数字化服务使数据收集变得容易,收集的数据发布与共享具有重要价值,例如,利用城市社交网络数据不仅可以优化道路设计,避免交通堵塞,还可以分析个人感兴趣的区域、用户的日常轨迹数据和居住地址,及具体分布,为决策提供支持。然而,数据发布与共享时,攻击者利用各种数据挖掘算法,使用户的隐私信息严重泄露[1],因此,需要保护其中的敏感信息不被泄露。经典的基于k-anonymity模型[2]隐私保护方法,易受最小性攻击、推理攻击和组合攻击等,难以提供足够的隐私安全。差分隐私保护[3-6]作为新兴的隐私保护方法,具有坚实的数学基础,即使攻击者掌握了最大的背景知识,也无法推理出用户的隐私信息,可以提供足够的隐私安全,在学术界和工业界都取得了很好的应用效果。其基本思想是向原始数据集或查询函数返回结果中添加满足Laplace分布的噪声,以达到隐私保护的目的。
1 相关工作

现有的这些隐私预算分配策略只适应特定的空间数据应用,用户不能根据数据的隐私保护需求,个性化选择合适的分配方式,来合理分配隐私预算,因此,本文提出等差数列分配法和等比数列分配法两种隐私预算ε分配策略,利用等差和等比数列的特征,用户通过调整差值或比值来灵活分配隐私预算,将给定的总的隐私预算分配给树结构的每一层;同时,本文通过数学证明和实验分析,验证了这两种方法能满足用户个性化设置差分隐私预算的需求。
2 基本概念
2.1 差分隐私
差分隐私一般要求任何两个数据集仅相差一个元组,随机算法的输出大约是相同的,即在输入数据集中添加或删除单个元组,对输出不会产生太大影响,即使攻击者具有任意背景知识,也无法从发布的查询输出中推断出任何个体信息的记录是否在数据集中,从而保护了敏感信息[14]。
定义1 相邻数据集[11]。如果D1和D2是相邻数据集,则D1和D2有着相同的属性结构,且仅相差一个元组,记为‖D1-D2‖=1。
定义2 差分隐私[11]。设D和D′为相邻的两个数据集,A为数据集上的随机算法,S是A任意一组可能的输出,如果Pr[A(D)∈S]≤eεPr[A(D′)∈S],则称算法A满足ε-差分隐私。其中,参数ε被称为隐私预算,ε越小隐私保护度越高,但是数据的利用率越低。
为了在给定的隐私预算内,将全部预算合理地分配到树结构各个节点中,使树结构整体满足隐私预算,可以利用差分隐私的一个基本性质。
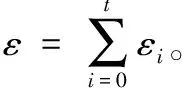
2.2 Laplace机制
自从Dwork等[3]引入差分隐私以来,Laplace机制成为差分隐私的标准工具。通过它向隐私数据统计信息中加入服从Laplace分布的噪声,以实现ε-差分隐私保护。
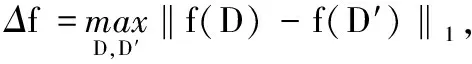
3 隐私预算分配策略
给定二维空间数据集D,向它加入服从Laplace分布的噪声后形成数据集D′,最终发布扰动后的数据集D′。本文的目标是根据用户对数据的隐私保护需求选择合适的分配方式,来合理分配隐私预算,因此,本文提出等差数列分配法和等比数列分配法两种隐私预算分配策略。
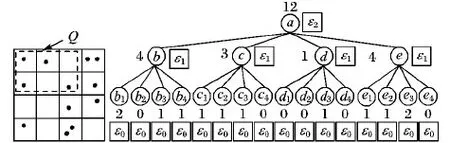
图1 四叉树索引隐私预算ε分配
3.1 等差数列分配法
从叶子节点所在的层次起,每一层次分配的隐私预算与它的上一层次的差等于同一常数d(d≥0),即将隐私预算ε0,ε1,ε2,…,εh分别分配给从0层到h层次的树结构,其中,εi=εh+(h-i)d。
由性质1可得:
(1)
由式(1)可得:
εh=ε/(h+1)-hd/2
(2)
把εh=ε/(h+1)-hd/2代入εi=εh+(h-i)d得:
εi=ε/(h+1)+(h/2-i)d
(3)
因为εi>0,同时d≥0,所以0≤d<2/[h(h+1)]。
综合以上可得:
εi=ε/(h+1)+(h/2-i)d; 0≤d<2/[h(h+1)]
(4)
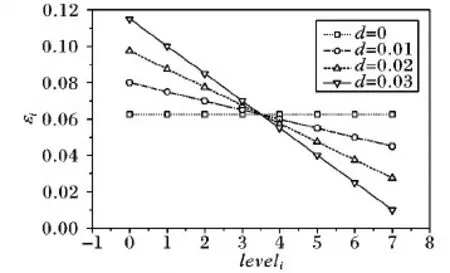
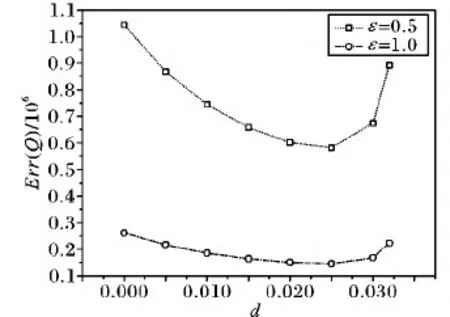
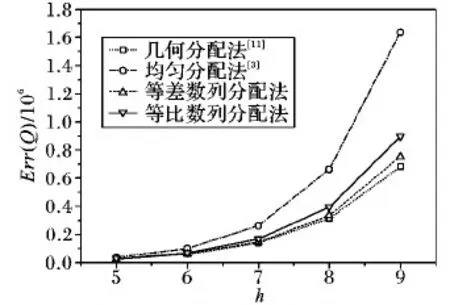
由以上分析可知,当给定总的隐私预算和树结构的高度,用户只需调整d值,就可以改变隐私预算的分配方式。当d值设置为0时,树结构每层分配的隐私预算相同,等同于均匀分配隐私预算。当0 从叶子节点所在的层次起,每一层次分配的隐私预算与它的上一层次的比等于同一常数q(q≥1),即将隐私预算ε0,ε1,ε2,…,εh分别分配给从0层到h层次的树结构的每一层,其中εi=εhqh-i(0≤i≤h)。 由性质1可得: (5) (6) 由式(5)~(6)可得: εh=ε(1-q)/(1-qh+1) (7) 将εh=ε(1-q)/(1-qh+1)代入εi=εhqh-i可得: εi=εqh-i(1-q)/(1-qh+1);q>1 (8) εi=ε/(h+1);q=1 (9) 综合以上可得: (10) 由以上分析可知,当给定总的隐私预算和树结构的高度,用户只需调整q值,就可以改变隐私预算的分配方式。当q值设置为1时,树结构每层分配的隐私预算相同,等同于均匀分配隐私预算。当q>1时,从根节点到叶子节点每层分配的隐私预算以q倍增加,不难理解,只要稍微改动公式就可以变成从叶子点到根节点每层分配的隐私预算以q倍增加。 本文提出的等差数列分配法和等比数列分配法算法详细描述,分别如算法1和算法2所示。 算法1 等差数列分配法。 Input:给定的总的隐私预算ε,树的高度h,参数d。 Output:每层的隐私预算。 Initialε、h和d; Create Tree(h,root); //创建树 Build Tree(h,root); //构建树索引 fori εi=ε/(h+1)+(h/2-i)d; GetNoise(εi); //获取Laplace噪声 end for if (root!=NULL) Count′=Count+Noise; for eachroot->child AddLaplace(root->child,hcount,Noise); //将噪声递归加入到其他节点中 end for end if outputεi 算法2 等比数列分配法。 Input:给定的总的隐私预算ε,树的高度h,参数q。 Output:每层的隐私预算。 Initialε、h和q; Create Tree(h,root); //创建树 Build Tree(h,root); //构建树索引 fori if (q=1) εi=ε/(h+1); else εi=εqh-i(1-q)/(1-qh+1); end if GetNoise(εi); //获取Laplace噪声 end for if (root!=NULL) Count′=Count+Noise; for eachroot->child AddLaplace(root->child,hcount,Noise); //将噪声递归加入到其他节点中 end for end if outputεi 以上两种算法中,用户只需调整相邻两层分配隐私预算的差值d或比值q,则可以动态改变隐私预算的分配方式,以满足用户的多样化需求。这两种算法将总的隐私预算分配给树的每一层的时间复杂度为O(n),以及将噪声添加到每个节点中的时间复杂度为均为O(nlbn),因此,这两种算法总的时间复杂度均为O(nlbn),且该算法简单易于理解。 对于任何查询函数Q(如图1中虚线矩形框),让Q′表示Q对树结构计算后的回答,那么Q′是对查询函数Q无偏估计的真实回答(此时加入的噪声为0),则方差D(Q′)是查询精确性的一个有力指标。同文献[8,11],本文也定义误差测量为Err(Q)=D(Q′)。 (11) (12) 为了检验本文所提等差和等比隐私预算分配方法的效果,本文从树结构每层分配的隐私预算、每层的查询误差和总的查询误差三个方面进行分析,并且与常用的均匀分配法和几何分配法进行分析和比较。 本文实验环境为:Intel Core i5- 6300HQ CPU @ 2.30 GHz,4 GB内存,Windows 10操作系统,Visual Studio 2015,C++语言实现,实验是基于四叉树索引结构。根据文献[15],当隐私预算0<ε≤1时,数据的可用性较好,可以更好地实现隐私保护的目的,因此,实验中总的隐私预算ε设置为0.1、0.5和1。假设查询函数为全局敏感度Δf是1的计数查询函数。 1)每层分配的隐私预算分析。 给定总的隐私预算ε为0.5,树结构的深度h为7,d值分别设置为0,0.01,0.02和0.03,树每层隐私预算分配如图2所示。 图2 不同d值下每层隐私预算分配对比 从图2可以看出,当d设置为0时,树结构每层分配的隐私预算相同;当d设置为0.01,0.02和0.03时,从根节点到叶子节点,每层分配的隐私预算呈线性增长。由于隐私预算的大小决定了隐私保护的力度,所以,当d=0时,树每层的隐私保护度相同;当0 2)每层的查询误差分析。 给定总的隐私预算ε为1,树深度h为7,d值分别设置为0,0.01,0.02,0.025和0.03,树每层查询误差Err(leveli)的变化如图3所示。 从图3可以看出,随着d值增加,根节点的Err(leveli)逐渐增加,叶子节点的Err(leveli)逐渐减小。当树高度一定时,每层的Err(leveli)由d值和所在层次的大小所决定,因此,当d分别设置为0,0.01和0.02时,从根节点到叶子节点,树每层的Err(leveli)均以指数级增长;当d设置为0.025和0.03时,从根节点到叶子节点,树结构每层的Err(leveli)是先减小后增加。以上说明,随着d值增加,Err(leveli)走势会改变,根节点的查询精确度越来越小,叶子节点的查询精确度越来越高,因此,用户可以根据对树结构每层查询精确度的不同需求,来灵活选择合适的隐私预算分配方式。 图3 不同d值下每层查询误差变化 3)总的查询误差分析。 给定总的隐私预算ε分别为0.5和1,树深度h为7时,则随着设置不同的d值,总误差Err(Q)变化情况如图4所示。 图4 d值对总查询误差影响 从图4可以看出,当d值一定时,随着ε值的增加,Err(Q)值逐渐减小,因此,给定总的隐私预算ε越高,整体查询精确度就越高。当ε值一定时,随着d值的增加,Err(Q)先减少后增加,且当d值无限接近于2/[h(h+1)]时,Err(Q)会急速增加到最大,这是因为d值接近2/[h(h+1)]时,根节点的Err(leveli)达到最大,进而导致总的误差Err(Q)最大。同时,不论h值如何变化,均会出现一个d值使Err(Q)达到最小值,不过这个值随着h的变化而变化,例如,当h=7时,d=0.024;当h=9时,d=0.018,因此,用户可以根据总的查询误差随着d值的变化情况,以及对总的查询精确度的不同需求,来灵活选择合适的隐私预算分配方式。 1)每层分配的隐私预算分析。 从图5可以看出,从根节点到叶子节点,每层分配的隐私预算逐级递增。当q设置为1.0时,树每层分配的隐私预算都相同;当q设置为1.05和1.1时,从根节点到叶子节点,每层分配的隐私预算几乎是呈线性增长;当q设置为1.26和1.415时,从根节点到叶子节点,每层分配的隐私预算呈指数增长。由于隐私预算的大小决定了隐私保护的力度,所以,当q=1时,树每层的隐私保护度相同;当q>1时,从根节点到叶子节点,隐私保护度越来越高,因此,用户可以根据对每层隐私保护度的不同需求,来调整q值,以选择合适的隐私预算分配方式。 图5 不同q值下每层隐私预算分配对比 2)每层的查询误差分析。 给定总的隐私预算ε为1,树深度h为7,q值分别设置为1.0,1.1,1.26,1.415和1.5时,树每层查询误差Err(leveli)的变化情况如图6所示。 图6 不同q值下每层的查询误差变化 从图6可以看出,当q分别设置为1.0,1.1和1.26时,从根节点到叶子节点,树每层的Err(leveli)是逐级递增;当q设置为1.415时,每层的Err(leveli)几乎相同;当q设置为1.5时,每层的Err(leveli)是逐级递减,因此,当q设置为1.415时,从根节点到叶子节点,树每层的查询精确度几乎相同;当1 当q值设置为1.415,树深度h为7时,分别给定总的隐私预算ε为0.1、0.5和1时,树每层查询误差Err(leveli)的变化情况如图7所示。 从图7可以看出,当q设置为1.415时,不管给定的总的隐私预算ε为何值,每层的查询误差Err(leveli)几乎相同,且给定的总的隐私预算越大,每层查询误差Err(leveli)越小。由此说明,当给定的总的隐私预算越大,树每层的查询精确度越高,且当q设置为1.415时,树每层的查询精确度几乎一致,因此当用户需要每层的查询精确度相同时,可以选择把q值设置为1.415的等比数列分配法,来合理分配隐私预算。 3)总的查询误差分析。 给定总的隐私预算ε分别为0.5和1,树深度h为7时,随着q值变化,总误差Err(Q)变化情况如图8所示。 图7 q是1.415时每层的查询误差变化 图8 q值对总查询误差影响 Dwork[15]指出隐私预算越小,则添加的噪声越大,提供的隐私保护度越大,但是数据的可用性越小,因此,数据的可用性受到隐私预算影响。从图2可知,在等差数列分配法下,当d=0时,每层分配的隐私预算相同;当0 本文将提出的等差数列分配法和等比数列分配法与隐私预算分配常用的均匀分配[3]和几何分配[11]两种方法作分析比较。分别从树结构每层查询误差和总的查询误差两个方面分析,实验结果如图9~10所示。 给定总的隐私预算ε为1,树深度h为7,其中等差数列分配法中设置d值为0.024,等比数列分配法中设置q为1.415,不同的隐私预算分配策略使树结构每层产生的查询误差的结果如图9所示。 图9 不同分配策略下每层查询误差对比 给定总的隐私预算ε为1,树深度h从5到9变化,其中等差数列分配法中针对不同的h值选择使总的查询误差达到最小的d值。为了与上面每层查询误差分析比较相一致,等比数列分配法中选择q值为1.415,不同的隐私预算分配策略产生总的查询误差结果如图10所示。 图10 不同分配策略下总的查询误差对比 虽然等差数列分配法和等比数列分配法均可以根据用户对数据隐私保护的不同需求来灵活分配隐私预算ε,但是等比数列分配法比等差数列分配法更加灵活,它具有以下优点。 1)树结构每层的查询精确度呈现规律性变化。图6表明等比数列分配法中随着q值的不同设置,树结构每层的查询精确度会呈现规律性的变化趋势。而等差数列分配法中随着d值的不同设置,树结构每层的查询精确度呈现无规律的变化趋势,且当d越接近2/[h(h+1)]时,树结构根节点的查询精确度会变得很低,从而导致总的查询精确度很低。 2)不受树深度h的限制。等差数列分配法中0≤d<2/[h(h+1)],d值的设置受到h的限制,当h值越大,d值的取值范围越小,当h值越小,d值的取值范围越大。而等比数列分配法中q≥1,不受树结构深度h的限制。 本文提出等差数列分配法和等比数列分配法两种隐私预算分配策略,能够满足用户自行选择的需求,可以根据隐私保护度和查询精确度分配隐私预算。只要将给定的总的隐私预算以等差数列和等比数列的特征分配给树的每一层,用户就可以根据对数据隐私保护程度的不同需求,通过调整相邻两层分配隐私预算的差值或比值,来改变隐私预算的分配方式,可以个性化设置隐私预算,改变了传统隐私预算均匀分配方法的不足。进一步对这两种方法作了分析比较,可知等比数列分配法比等差数列分配法更加灵活。 本文提出的两种分配策略,考虑的只是数值型数据,并没有对非数值数据或混合型数据进行研究,下一步将对此作更加深入的研究。3.2 等比数列分配法
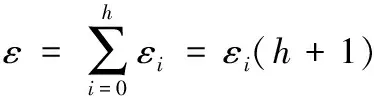
3.3 算法实现
3.4 查询误差
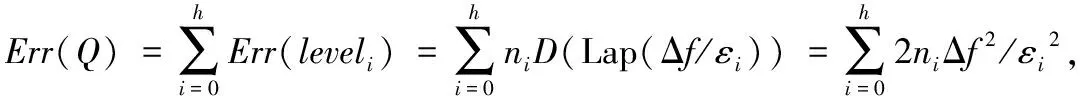
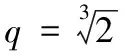
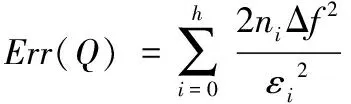
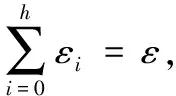
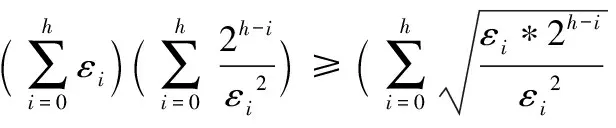
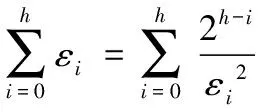
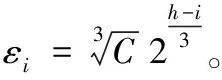

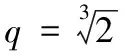
4 实验结果与分析
4.1 等差数列分配法分析

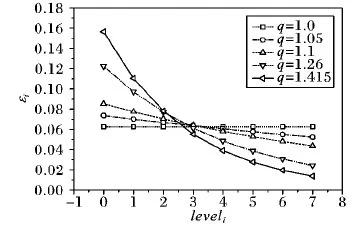
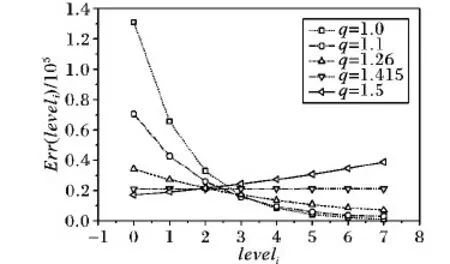
4.2 等比数列分配法分析
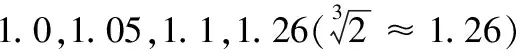
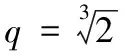


4.3 数据可用性分析
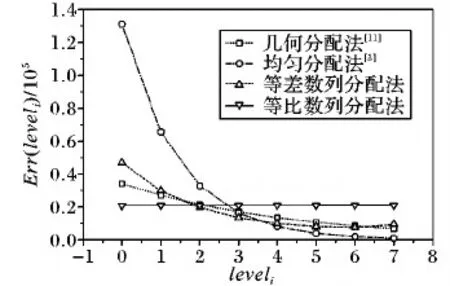
4.4 与其他分配策略的比较
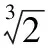
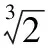
4.5 等差数列分配法与等比数列分配法的比较
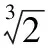
5 结语
