Niederreiter公钥密码方案的改进

刘相信，杨晓元

(网络与信息安全武警部队重点实验室(武警工程大学)，西安 710086)(*通信作者电子邮箱1125424226@qq.com)

0 引言

基于编码的密码方案具有抗量子的特性和简单的加解密过程，是当今抗量子密码方案的佼佼者。1978年，Berlekamp等[1]证明了随机线性码的译码问题是一个非确定性多项式完全困难(Non-deterministic Polynomial Complete, NPC)问题，为基于编码的公钥密码方案的设计奠定了理论基础，同年McEliece[2]利用此困难问题提出第一个基于Goppa码的公钥密码方案——McEliece公钥密码方案。该方案可抗量子攻击、加解密速度快、实现简单。方案中错误向量的汉明重量固定且公开，易导致密文对明文信息的泄露，所以必须选取较大的公钥尺寸来保证计算安全性，因此该方案公钥尺寸过大，实用性差。1986年，Niederreiter[3]对McEliece公钥密码方案进行了改进，提出了一种Niederreiter公钥密码方案，该方案从另一个角度利用了随机线性码的译码困难问题，McEliece公钥密码方案隐藏的是Goppa码的生成矩阵，而该方案隐藏的是Goppa码的校验矩阵，此时公钥尺寸有所变小，但还是没有达到实用要求。为了降低方案的密钥尺寸、提高方案的性能，同时保持方案的安全性，学者们纷纷利用一些具有较好性质的线性码来代替原方案的Goppa码，例如RM(Reed Muller)码、LDPC(Lower Density Parity Check)/MDPC(Moderate Density Parity Check)码、RS(Reed-Solomon)/GRS(Generalized RS)码、QC(Quasi-Cyclic)/QD(Quasi-Dyadic)/QM(Quasi-Monoidic)码、代数几何码等，这些方案虽然具有较好的性能，但是这些好的性能是以牺牲原始McEliece和Niederreiter方案的安全性为代价的。

随着最新研究的推进，大量的改进方案均被证实存有漏洞。文献[4-7]是近几年出现对于QC密码方案的攻击，指出现有QC-LDPC(Quasi-Cyclic Low-Density Parity-Check)编码密码方案和QC-MDPC(Quasi-Cyclic Medium-Density Parity-Check)编码密码方案均存有漏洞。文献[8]指出通过Goppa码或者交替码的子族来生成紧凑公钥的方案是存有漏洞的，即现有QC/QD/QM编码密码方案是存有漏洞的。文献[9-10]指出采用Goppa码的原McEliece方案在某些参数下存有与随机码相区分的区分器，并对其进行了密钥恢复攻击。文献[11]采用GRS码的平方码构造与随机码相区分的区分器，对一些GRS码的变形方案进行了多项式时间的密钥恢复攻击。特别强调的是，现有的编码密码方案均无法抵抗信息集攻击(Information Set Decoding, ISD)，且这种攻击方法在不断的优化和应用[12-17]。

2016年，Baldi等[18]从一个崭新的角度对McEliece密码方案进行了改进，将现有McEliece密码方案中的置换矩阵P改为Q=R+T，前者为稠密的，后者为稀疏的，以提高密钥隐藏能力，设计的方案在某些参数下可以抵抗区分攻击，但是无法抵抗ISD。

本文认同Baldi等[18]的观点，即单纯地用置换矩阵去隐藏密钥的方法是不能够真正地隐藏密钥信息，产生的公开码字与原秘密码字是置换等价的。为此本文对Niederreiter密码方案中的置换矩阵P进行改进，使P为随机矩阵，唯一的要求是其列重的最大值固定。需要注意的是，在线性码纠错能力有限的情况下，这样改进的同时会大幅度降低错误向量e的汉明重量，进而指数级地降低ISD的代价。为此本文对置换矩阵P改进的同时，对错误向量e也进行了随机拆分，使其汉明重量变大且未知(也可能超过线性码的纠错能力)，以抵抗ISD，由此实现对Niederreiter密码方案的改进。GRS码具有灵活的参数选取方法和有效的译码方法，本文借鉴文献[18]的方法，用GRS码测试方案的性能；结果表明，改进Niederreiter密码方案可以抵抗区分攻击和ISD，表现出较好的性能，在量子时代下的生存力增强。

1 基础知识

1.1 编码理论中的NPC问题

1978年，Berlekamp等[1]证明了随机线性码的译码问题是NPC问题，为基于编码的公钥密码方案的设计奠定了理论基础。其表述如下：

1.2 Niederreiter密码方案

设(n-k)×n阶矩阵H为二元(n,k,d)Goppa码的校验矩阵，其中n=2a，d=2t+1，k=n-at。快速译码算法ΨH(t)。

1.2.1 密钥生成

随机选取GF(2)上的(n-k)×(n-k)阶可逆矩阵A和n×n阶置换矩阵P，计算H′=AHP，将A、H、P作为私钥保存，H′作为公钥公开。

1.2.2 加密过程

明文m∈GF(2n)的汉明重量为t。密文：c=mH′T。

1.2.3 解密过程

接收方收到密文c后，计算cA-1T=mH′TA-1T=mPTHTATA-1T=mPTHT，利用Goppa码的快速译码算法可得m′=mPT，进而得m=m′(PT)-1。

在此本文对Niederreiter密码方案进行如下阐述说明:第一，方案中的公钥H′=AHP通过私钥H左乘可逆矩阵A和右乘置换矩阵P得到；由矩阵的性质可知，矩阵的左乘相当于对矩阵的行作变换，故私钥H左乘可逆矩阵A并不能改变线性码的性质，因此无法真正地隐藏私钥H；矩阵的右乘相当于对矩阵的列作变换，私钥H通过右乘置换矩阵P得到HP，其作用仅仅是对其进行了简单的置换，校验矩阵HP与校验矩阵H生成的码字是置换等价的，因此也无法真正地将私钥H隐藏；即公钥H′没有真正地将私钥H的信息完全隐藏，这是现有编码密码方案容易遭受区分攻击的根本原因。第二，方案中的明文信息的汉明重量固定且公开，这是现有编码密码方案容易遭受ISD的根本原因。

2 Niederreiter密码方案的改进

本文从两方面对Niederreiter密码方案进行改进：第一，对方案中的置换矩阵P进行改进，使P为随机矩阵，唯一的要求是其列重的最大值固定；第二，对错误向量e进行改进，隐藏其汉明重量。方案如下。

2.1 密钥生成

(n-k)×n阶矩阵H为二元(n,k,d)GRS码的校验矩阵，其纠错能力为t，快速译码算法ΨH(t)。随机将H拆分为两个矩阵H1和H2，使得H=H1+H2。随机选取三个(n-k)×(n-k)阶可逆矩阵A、B和C，随机选取一个n×n可逆矩阵Q且其列重最大值为w(无需公开)。分别计算H′=AH1Q、H″=BH2Q、H‴=CHQ、ts=⎣t/w」。将(H′,H″,H‴,ts)公开，(A-1T,B-1T,C-1T,Q-1T,ΨH(t))秘密保存。

2.2 加密过程

2.3 解密过程

当接收方收到密文(c1,c2,c3)后，进行下列运算：

c3C-1T=e2H‴TC-1T=e2QTHTCTC-1T=e2QTHT

因为e=e1+e2、H=H1+H2，故c1A-1T+c2B-1T+c3C-1T=eQTHT；此时，wt(eQT)=ts·w=⎣t/w」·w≤t，故在GRS码的纠错能力之内，因此利用GRS码的译码算法ΨH(t)对c1A-1T+c2B-1T+c3C-1T进行译码可得到eQT，进而得到e=eQT·Q-1T，解码即可得到明文m。

3 安全性分析

目前对于Niederreiter密码方案的攻击方法有两类：区分攻击和ISD。前者试图将公钥与随机矩阵区分开来，进一步实施密钥恢复攻击；后者旨在从获取的密文直接恢复明文。

3.1 区分攻击

区分攻击的思想是将一个随机矩阵与公开码字的生成矩阵或者校验矩阵(即公钥)区分开来，针对不同的方案可以实施具体的区分操作，进行密钥恢复攻击，且其花费的代价较小，如文献[9-11，19]。

在改进的Niederreiter密码方案中，本文将私钥矩阵H右乘了一个随机矩阵Q，得到的矩阵HQ已经不再是某个线性码的校验矩阵，具有随机性，且攻击者不知道密文中e1和e2的汉明重量；此时攻击者无法将公钥中的(H′,H″,H‴)与随机矩阵区分开来，无法进行密钥恢复攻击，进而无法构造等价码进行解码操作，所以本方案可以抵抗区分攻击。

3.2 ISD

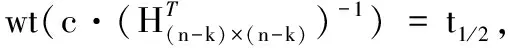
4 性能分析

表1 两种方案的密钥尺寸比较(F2)

5 结语

基于编码的公钥密码方案作为抗量子方案的备用方案之一，具有较高的安全性和较好的性能，很有可能成为量子计算机时代下保障数据安全的关键技术。本文对Niederreiter密码方案进行了深入的阐述，对现有研究现状作了归纳总结；结合Baldi等[18]的最新研究成果，并受其启发，对原Niederreiter密码方案中的置换矩阵和错误向量进行了改进，对改进Niederreiter密码方案的安全性进行了深入细致的分析，利用GRS码测试了方案的性能。分析表明，改进Niederreiter密码方案可以抵抗区分攻击和ISD；测试表明，改进方案表现出较好的性能，在量子时代下的生存力增强。需要注意的是，改进方案从理论上证明了其优越性，在具体的应用场景下，应根据具体的需求灵活地选取合适的线性码和参数。