基于带电粒子搜索的无人潜航器航路规划方法

赵云钦，蔡 超，王厚军，李东武

(1.多谱信息处理技术国家级重点实验室(华中科技大学 自动化学院)，武汉 430074；2.国家海洋技术中心，天津 300112； 3.天津航天中为数据系统科技有限公司，天津 300450)(*通信作者电子邮箱caichao@hust.edu.cn)

0 引言

无人潜航器(Unmanned Underwater Vehicle, UUV)是一种能在水下自主远程航行的智能化装置，它能够完成水下搜寻、侦察，甚至是军事上的进攻防守等任务[1-2]。如今海洋开发日益加快，无人潜航器得到了各个国家的重视，不管是在军事领域还是在民用领域都发挥着越来越重要的作用。航路规划是UUV研究领域中的热点问题之一，它是指在综合考虑航行器自身性能、能量损耗、威胁以及航行区域限制的情况下，在起始点和目标点之间规划出一条最优或可行的航路[3]。

UUV航路规划具有规划区域广阔、环境复杂、约束条件多等特点，这就对航路规划算法的收敛速度、内存空间需求都有比较高的要求。国内外学者在航路规划算法方面作了许多研究工作，也提出了多种航路规划算法。Kanehara等[4]通过采用地图格网化的方法将航路规划问题离散化，然后采用A*算法找到最短路径；但是A*算法作为一种确定性算法，它的计算复杂度和规划时间将随着规划区域的增大也将大幅上升。也有学者采用随机性算法进行航路规划，如Khelchandra等[5]提出一种基于随机采样的航路规划方法，该方法虽然能够以比较高的概率在短时间内规划出一条路径，但是也有可能规划出一条不可行的路径；Tarokh等[6]采用的遗传算法，但是由于各种约束的存在，该方法会出现早熟而导致得不到最优解；Englot等[7]也提出了基于蚁群算法的航路规划方法，但对于连续的规划空间，算法收敛速度慢，规划用时长；而粒子群优化(Particle Swarm Optimization, PSO)算法[8]参数设置比较复杂，局部搜索能力不佳，收敛速度慢。

带电粒子搜索算法最早在2010年由Kaveh等[9]提出，它源于物理学中库伦定律和牛顿定律的启发，通过搜索空间中带电粒子的相互作用，进而达到寻优的目的。该算法对于优化问题在保证解质量的同时可以得到更快的收敛速度。自带电粒子搜索(Charged System Search, CSS)算法提出以来，已经在多个领域得到了应用。Kaveh等[10]将CSS算法离散化并将其用于框架结构优化问题的求解；Özyön等[11]将该算法用于电力调度问题，以减少传输消耗和NOx等有毒化学物质的释放；Precup等[12]将该算法用于模糊控制器的优化。

本文将带电粒子搜索算法与航路规划问题相结合，提出一种基于带电粒子搜索的航路规划方法。本文对航行器航路规划问题进行建模，采用标准矢量电子海图作为搜索空间，使用实数编码的带电粒子来表示航路，通过建立代价函数将多约束、复杂海洋环境下航路规划的多目标优化问题转换为单目标优化问题，并用该方法对最终的单目标问题进行优化求解。实验分析表明该方法在保证规划出的航路质量的同时，收敛速度快、规划耗时短。

1 UUV航路规划问题及模型建立

1.1 UUV航路规划问题

UUV航行在复杂的海洋环境中，为了保证航行器的安全航行不仅要考虑到海洋自然环境约束(如：洋流、风浪、海底地形等)，还需考虑导航区域约束、战场环境约束等。航路规划要在综合考虑多种因素的条件下，为航行器规划出一条安全的，能够顺利完成目标任务的航路，因此航路规划问题实质上是一个带约束的多目标优化问题：

目标函数 minfit(X)=[f1(X),f2(X),…,fn(X)]T

约 束gi(X)≤0;i=1,2,…,p

hj(X)=0;i=1,2,…,q

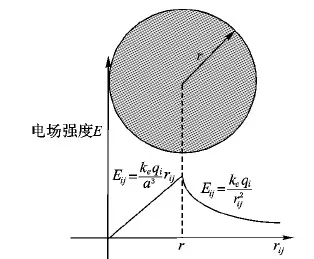
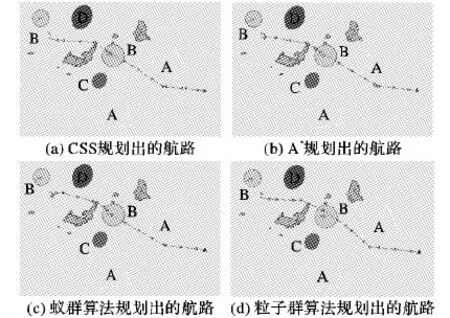
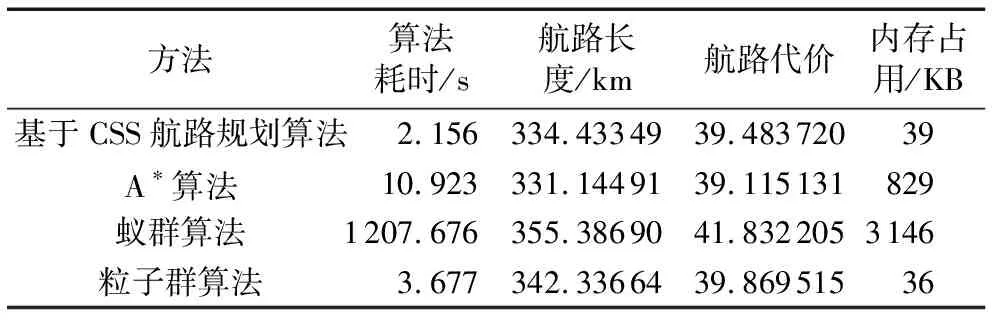
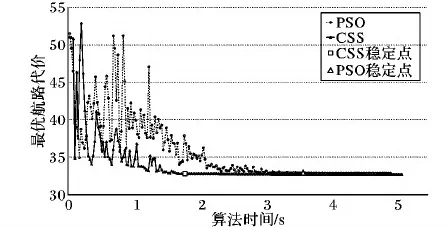
Xl

决策变量X={X1,X2,…,Xm}

其中：Xl、Xu分别为决策变量X的下界和上界，决策变量的边界值就构成了目标问题的决策空；fi(X)(i=1,2,…,n)表示n个需要被同时优化的目标函数；gi(X)≤0(i=1,2,…,p)表示p个不等式约束函数；而hj(X)=0(i=1,2,…,q)表示q个等式约束函数。

多目标优化问题往往包含了多个相互耦合的目标函数，它可能没有唯一的最优解，而是一个包含无穷多个解的解集。最后，决策者需要对Pareto解集中的解作比较并进行选择，因此，UUV航路规划中的模型建立和代价函数设计就是其中尤为关键的两个部分。

1.2 模型建立

UUV在海洋环境中航行时，会受到自身物理性能限制[13]，主要有以下几个方面：

1)航行器转弯约束：UUV转弯时，最大转弯角度不能超过θmax，最小转弯半径不能小于Rmin：

2)安全航行深度约束：为了保证UUV的航行安全，其航行深度h应该小于当前位置海洋深度hsea，0

3)最大航程约束：UUV由于机载能耗有限，所以航路距离l不能超过其最大航程lmax，l

4)上浮约束：UUV在没有海洋浮标的海域中，为了能够及时校正航路偏差，可以采用让UUV上浮与卫星进行通信的方法，因此，航路需要在除风浪区以外的位置每隔一定时间设置一个上浮点使UUV完成卫星通信。

海洋环境复杂且范围广，合适的地图环境描述与存储方式对规划精度和速度都有重要的影响。本文采用的是标准的矢量电子海图来描述环境信息，它将海域中的每个要素都以点、线、面等几何元素的形式存储下来，相比栅格电子海图具有存储量小、精度高等优点，并且当环境发生改变时，用户可以方便地在基础数据上进行修改更新。

由于海洋环境复杂，而环境因素对UUV航路规划影响很大。为了便于算法的模拟计算，本文将海洋环境表达为以下几种约束区域模型。

1)限制区：岛屿、禁飞区、暗礁等航行器不可达的区域，在本文中用凸多边形来描述限制区。

2)威胁区：在某些区域，敌方在一些区域会部署雷达、防御武器等，这对航行器的安全性产生威胁，在航路规划时应尽量避开这些区域。本文用椭圆来描述威胁区，当航行器进入这类区域时，航行器有一定可能被拦截摧毁。穿过的威胁区的威胁等级越高，航行器被拦截的概率越大。

3)海流区：在海洋中的不同区域、不同深度海流的大小和方向是不同的，这对航行器的速度矢量产生影响，因此，在航路规划时必须考虑到海流因素的影响，航行器在海流区中的航行速度是正常巡航速度与海流速度的矢量叠加。

4)风浪区：在某些海域表面，由于风的作用会引起海水的波动。航行器在这类区域上浮将会对自身安全性造成影响，因此在风浪区航行器不能进行上浮以及与卫星进行通信操作。由于在此区域无法进行通信进而对当前航线进行误差矫正，这就会使航行器偏离既定航路。为了保证航行器的安全准确航行，需要绕过风浪区航行。

1.3 航路表示与代价计算

根据不同的实际要求、不同抽象层次，航行器的航路可以表达成多种形式。Capozzi[14]提出几种典型的航路表达形式：

1)航行器空间位置点序列；

2)航行器速度和方向的时间序列；

3)航行器机动动作的时间序列；

4)任务级的抽象航路。

这四种航路表达方式抽象程度依次增加。无论采用什么表达形式，都应以有利于航路规划计算与航路的准确表达为首要目标。本文采用空间位置点序列表示航行器航路，例如：S表示起始点位置，T表示目标点位置，X1,X2,…,Xm为中间航路点位置，航路就可以表示为：

{S,X1,X2,…,Xm,T}

因此航路规划问题实质上是在规划空间中找到一个满足要求的m维的解向量。

本文综合考虑了UUV的航程、海流、威胁等因素，将代价评估函数设置如下：

(1)

其中,f(xi)表示航路段xi的代价，它由时间代价ft和威胁代价fs组成。

2 基于带电粒子搜索的航路规划方法

2.1 CSS算法描述

带电粒子搜索算法受到库伦定律和牛顿定律的启发，利用带电粒子之间的相互作用来进行寻优，是一种具有全局搜索能力的智能算法。与蚁群算法、粒子群算法等智能算法相比，该算法中每个带电粒子之间有更多的信息交流，它具有较强的全局搜索能力和更快的收敛速度等特点。

该算法首先会在规划空间中随机初始化一组初始解(称为初始带电粒子群)P={p1,p2,…,pn}，每个带电粒子pi都被看成为一个半径为a的带电球体，其所带电荷量qi由代价函数值确定，它将会在其周围区域产生一定强度的电场，如图1所示。在电磁场中带电粒子的电荷量越大，该带电粒子对其他带电粒子的吸引力就越大，通过电场力的影响，每个带电粒子在规划空间中进行寻优。在本方法中，利用代价值来间接表征带电粒子的电荷量大小，电荷量越大则对其他带电粒子的吸引力就越强，其他带电粒子从该粒子继承信息的继承度就越高。

图1 电场强度示意图

根据库伦定律，带电粒子在电场中会受到电场力的作用，如下式所示：

其中：Eij表示电场强度；qj表示带电粒子j的电荷量；ri和rj分别表示带电粒子i，j的空间位置，因此在搜索空间中，带电粒子会受到其他粒子产生的电场的影响，进而在空间中进行移动寻优。在每次迭代时，带电粒子根据如下式进行位置、速度更新：

Xj,old

Vj,new=(Xj,new-Xj,old)/Δt

其中:ka是加速度系数，kv是速度系数；Fj是带电粒子j所受电场力合力;Δt是时间步长;Xj,new、Vj,new分别为位置和速度矢量；randj1和randj2都是均匀分布在(0，1)上的随机数。该方法通过计算其他带电粒子施加给当前粒子的合力来确定该带电粒子更新后的位置、速度等。重复迭代过程，直至满足定义的算法终止条件后，停止迭代并得到优化问题的解。

2.2 基于CSS的航路规划方法

由1.3节的分析，航路规划问题最终目标是要在规划空间中得到满足要求的一个m维的解向量；因此在本文方法中，每个带电粒子都被视为规划空间中的一个解，并且解代表的航路的优劣程度由上文航路代价部分描述方法来进行度量。通过代价值再对每个带电粒子自适应更新其所带电荷量，提高算法的收敛速度和自适应能力。记带电粒子集合为P，它由n个带电粒子组成：P={p1,p2,…,pn}，带电粒子pi代表规划空间中的一条航路。对于任意带电粒子pi，可以由式(1)计算得到该带电粒子所代表航路的代价函数值fiti，故带电粒子集合的代价为：

fit=[fit1,fit2,…,fitn]

因而可以根据代价函数值得到该带电粒子群中的最优带电粒子pbest和最差带电粒子pworst，以及它们分别的代价函数fitbest和fitworst：

pbest=min(fit1,fit2,…,fitn)

pworst=max(fit1,fit2,…,fitn)

较优的带电粒子相比较差的粒子应该在搜索寻优过程中发挥更重要的作用，因此，带电粒子电荷量大小可以和代价函数值关联起来。

在迭代过程中每个带电粒子的电荷量、电场力以及位置速度计算方法定义如下：

1)电荷量。对于带电粒子pi，将其电荷量qi通过上文定义的代价函数值，采用归一化的方法来进行定义：

(2)

可以看出越优的带电粒子其代价函数值越小，而所带电荷量越大。这使得该带电粒子对其他的粒子产生更大的电场力，进而使较差的粒子朝着较优的粒子运动。

2)带电粒子间距离。本文所考虑优化问题的解空间是一个m维空间，其中任意两个带电粒子pi、pj的距离采用如式(3)进行计算：

(3)

其中：Xi、Xj分别是带电粒子pi和pj的位置，都是一个m维的向量；Xbest是当前最优粒子pbest的位置;ε是个极小正数，防止分母为0。

3)电场力。带电粒子所受电场力合力的计算可将当前带电粒子所获得的局部和全局信息有效地结合起来，为航路规划算法优化搜索提供依据。带电粒子pj在维度k上所受电场力合力：

(4)

其中i1、i2为：

pij表示带电粒子pj受到粒子pi电场力的概率：

其中rand是在(0，1)范围内均匀分布的随机数。根据矢量叠加，最终可以得到带电粒子pj所受到的电场力合力Fj：

Fj=[Fj1,Fj2,…,Fjm]

在最初的迭代搜索过程中，带电粒子彼此之间离得都比较远，而此时库仑力反比于带电粒子距离的平方。在这种情况下，早期的迭代过程中带电粒子会进行更多的全局搜索，因此算法具有较强的探索能力。对于随机性算法而言，在算法开始的时候增强全局搜索能力，随着迭代的进行减小这种全局搜索是必要的。经过一系列的迭代搜索过后，带电粒子聚集在一个小的区域，故而带电粒子间的距离变小，此时带电粒子所受到的电场力合力正比于带电粒子距离，开始进行精细的局部搜索，并且，这个阶段带电粒子所受电场力合力始终正比于其电荷量。较优的带电粒子具有较小的代价函数值，故而带有较高的电荷量，在它的周围将会有较大的电场强度；也就相对于较差的带电粒子而言，它对其他的粒子将会产生较大的吸引力，所以带电粒子朝着好的粒子运动的趋势将会大于朝着差的粒子运动的趋势。

4)位置、速度更新。根据库伦定律和牛顿运动定律，每次迭代规划空间中的带电粒子pj的每个维度k的位置速度分量将按如下公式进行更新：

(5)

vjk(t+1)=xjk(t+1)-xjk(t)

(6)

其中：ka是加速度系数，用来调控其他带电粒子对位置更新的影响；kv是速度系数，用来调控先前带电粒子速度的影响；randj1和randj2都是均匀分布在(0，1)上的随机数。ka与带电粒子的电场力合力相关联，较大的取值将会导致过快的收敛；较小的取值将会使收敛速度变慢，增加计算时间。而kv则平衡着全局搜索能力与局部搜索能力，kv较大则全局搜索能力强局部搜索能力弱，反之则全局搜索能力弱、局部搜索能力强。在算法开始阶段，全局搜索能力较强，随着迭代搜索的进行，全局搜索能力减弱、局部搜索能力增强，这样才能达到好的寻优效果，因此，本文将ka和kv设置如下：

(7)

(8)

其中：iter是当前迭代次数；itermax是算法最大迭代次数。由式(3)和(4)可知，kv从初始值1开始，随着迭代次数iter的增加，非线性递减；ka则随着迭代次数增加，非线性单调递增。随着搜索算法进入迭代后期局部搜索阶段kv减小，ka增大速度变快，这避免了带电粒子因速度过快而使算法无法在当前最优区域进行更加精细的搜索。通过这种方法来平衡全局搜索与收敛速度，可以有效地避免算法的早熟收敛。

2.3 方法流程

基于CSS的航路规划算法的流程如图2所示，方法的具体步骤描述如下：

1)根据实际问题设置合适的带电粒子个数m，最大迭代次数itermax，算法终止条件；

2)根据航路规划任务的要求，设置每个带电粒子的维数；

3)初始化整个带电粒子群，每个带电粒子代表规划空间中的一条航路，初始化每个带电粒子的位置、速度；

4)根据设定的代价函数，计算出每个带电粒子的电荷量；

5)计算带电粒子所受电场力合力，更新带电粒子的位置及速度；

6)更新每个带电粒子的代价函数值；

7)确定是否达到终止条件，如果没有，返回到步骤4)，否则算法结束；

8)输出全局最优代价函数值的带电粒子所代表的航路。

图2 基于CSS的航路规划方法流程

3 实验结果及分析

本文在Intel Core i5- 3230M CPU、2.60 GHz、4 GB内存的PC上进行仿真实验，运行环境为Windows 7，编程环境为VS2005。

相关实验参数设置为：带电粒子群规模m为30。约束条件设置为：航行器最大转弯角度60°，最小转弯半径200 m，上浮时间间隔为4 h。算法终止条件为：连续两次迭代最优代价值相差小于0.01，则算法终止。

本实验采用的是矢量电子海图，地图范围为116.2°E～132.5°E，21.5°N～41.2°N，约为1 793 km×2 167 km的矩形区域。记号“”表示航行器的起始点，“▲”表示目标点，其中限制区标注为“A”，海流区标注为“B”,风浪区标注为“C”，威胁区标注为“D”。

实验中对本文方法与A*算法、粒子群算法和蚁群算法进行多组对比实验，每次对比实验以上四种方法均在同样的起始点、目标点以及相同海域环境下进行实验，记录每种方法每次实验规划得到的航路代价、实验耗时和占用内存。其中：蚁群算法设置为迭代5次终止，信息素挥发因子为0.3，蚂蚁数为20；粒子群算法种群数目设置为30，终止条件设置为连续两次迭代最优代价值相差小于0.01，则算法终止。在不同海域环境下得到的航路规划实验结果如图3、图4所示。

从表1、表2实验数据可以看出，航路规划算法用时上从小到大依次为：基于带电粒子搜索的航路规划方法、粒子群算法、A*算法、蚁群航路规划算法。为了对本文方法与粒子群航路规划方法作进一步比较，本文对每组实验记录了这两种方法最优航路代价的收敛曲线，如图5、图6所示。在相同的实验条件下，本文方法得到的航路的代价值与粒子群算法航路代价值相差不大；但收敛速度比粒子群算法收敛速度快。这是因为在粒子群算法中，粒子的运动仅由局部最优和全局最优来决定，这样大部分其他粒子所携带的信息都被忽略。这也是本文方法与粒子群算法的一个本质不同，在本方法中，每个带电粒子的运动是由其他带电粒子对其电场力合力来确定的，每次迭代寻优是综合了其他带电粒子影响的结果，带电粒子之间有更多的信息交流。这一特点就使得带电粒子能够以一定概率更新到远离当前局部最优的位置，而这个位置可能比当前全局最优粒具有更好的适应度，因此该算法相比粒子群算法具有更强的全局搜索能力；并且本文提出的非线性调整速度和加速度系数的方法平衡了全局搜索与局部搜索，在提高了算法收敛速度的同时，避免了算法的早熟。

图3 绕岛屿航路规划实验

图4 复杂环境航路规划实验

方法算法耗时/s航路长度/km航路代价内存占用/KB基于CSS航路规划算法1.786292.8869632.82670234A∗算法6.314291.5927332.681645646蚁群算法213.804313.2360134.3441802361粒子群算法3.598294.3106432.89878133

表2 复杂环境航路规划实验结果比较

从以上两组实验结果看，本文方法与确定性算法A*算法相比，A*算法最终规划出的航路代价略优；但是本文方法规划用时间明显少于A*算法。在规划空间环境比较复杂的情况下，A*算法会占用大量内存。从表1、表2实验结果可以看出，当规划空间变得相对复杂时A*算法在第二组实验中内存消耗比第一组实验提高了28.3%，而本文方法内存消耗没有太大变化，并且A*算法在复杂环境下寻优过程中可能会产生回退，这会使算法耗时增大，而本文方法则不存在该问题。

图5 绕岛屿航路规划实验CSS与PSO最优航路代价收敛曲线

图6 复杂环境航路规划实验CSS与PSO最优航路代价收敛曲线

蚁群算法也是一种随机性算法，它基于蚂蚁信息素这种间接交流方式，是一种离散的优化方法。该算法本质上是一种正反馈机制，最优路径上的蚂蚁增多，留下的信息素强度变大，导致后面的蚂蚁通过轮盘赌更大的概率会选择到该路径，最优路径上的蚂蚁数量更多，最后收敛到这条路径上。对于离散的搜索空间(如Voronoi图等)，蚁群算法耗时和优化结果都有较好的效果；但是对于连续的搜索空间，信息素的扩散等操作将会使得算法耗费的时间大幅度增加，信息素图也会占用大量内存，而本文提出的方法对于连续问题的求解则没有这一问题。从表1、表2也可以看出，本文方法与蚁群算法解的质量相差无几，但是该方法所用时间以及占用内存都远小于蚁群算法。

4 结语

本文提出了基于带电粒子搜索的航路规划方法，并成功地将该方法运用于无人潜航器的航路规划，有效地解决了多约束复杂海洋环境下的航路规划问题。通过实验表明，该方法能够快速为航行器规划出可行航路，并通过对比实验表明，该方法与A*算法、蚁群算法、粒子群航路规划算法相比，在保证解的质量的同时，算法耗时较少，收敛速度更快。本文航路规划方法对于特定的任务带电粒子的维数是固定的，因此下一步可以将本方法中的带电粒子的维数引入模糊性，而不是设置为固定的维数，这会使得本方法在适应高维问题的同时，优化效果进一步提高。