利用GeoGebra3D视图创设鲜活的光的干涉情景

曾 燕 殷正徐

(1. 江苏省常熟中学,江苏 常熟 215500; 2. 江苏省沭阳高级中学,江苏 沭阳 223600)

1 问题的提出

干涉是波特有的现象,杨氏干涉实验是认识光之本性的里程碑．教材中“光的干涉”一课用图1研究了光的干涉,笔者觉得有3处值得商榷: (1) 用光线代替光波; (2) 忽视干涉的空间性; (3) 对“决定条纹间距的条件”有名无实．笔者觉得主要原因乃是教材编者受到教材载体的束缚,尽管考虑得周全,但其主张只能在二维纸面书写,难以详尽表达其想法．所以,无论教材重编多少次,只要载体还是纸张,就无法彻底解决这个难题．

图1 教材研究光的干涉原图

编者的难题应由教师借助多媒体来解决．本文应用的多媒体软件GeoGebra,它是一款动态几何软件,开源免费,比几何画板功能强大,可以绘制点、线段、射线、向量、多边形、曲线、函数等等,用户也可以在命令栏直接输入方程或点坐标进行绘图,有代数区、表格区、运算区、绘图1区、绘图2区和3D绘图区等．本文重点介绍利用GeoGebra 3D绘图功能打造生动鲜活的干涉情景,帮助学生全面深入理解干涉机制．

2 课件制作

(1) 建立干涉场景.

① 打开GeoGebra 3D绘图区,改变其默认设置:显示x轴,显示y轴但隐藏其数值与刻度,隐藏z轴．

图2 光的干涉情景

② 用描点工具单击y轴,设定为点S1,在命令栏输入:S_2=(0,-y(S_1),0)(备注:在GeoGebra命令栏中,下划线“_”后表示下标,如S2在命令栏中表示成“S_2”,下同);在y轴上绘制点S2,与S1关于x轴对称．S1和S2用来模拟双缝．

③ 单击滑动条工具新建变量L,数值范围[1,20],表示双缝到光屏之间的距离;在命令栏输入:曲面(u,v, 0,u, 0,L,v,-20, 20),新建平面a表示波的平衡位置,在命令栏输入:曲面(L,u,v,u,-20, 20,v, 0, 3),新建平面b(垂直于平面a)模拟光屏．效果如图2所示．

(2) 制作相干光波.

① 设定光波参数．利用滑动条工具,设置两列波的振幅A1=1,A2=1,变化范围为[0.5,1,5],设置两列波的波长λ1=4 m,λ2=4 m,变化范围为[3, 5],设置两列波的圆频率ω1=1,ω2=1,变化范围为[1,2]．

② 作平面a与平面b的交点,得到直线f,用描点工具单击直线f,得到点P,点P可以在直线f上自由移动;设S1P与x轴正方向的夹角为α1,在命令栏输入:α_1=atan2(y(P)-y(S_1),x(P)-x(S_1)),即可得到α1的数值,同理在命令栏输入:α_2=atan2(y(P)-y(S_2),x(P)-x(S_2))得到S2P与x轴正方向的夹角α2;利用滑动条工具创建变量t,用于模拟时间,变化范围为[0,100]．

③ 在命令栏输入:曲线((x(S_1)+sx, y(S_1)+tan(α_1) sx, A_1 cos(ψ_1-k_1 sx/cos(α_1)+ω_1 t)), sx, 0, L),得到从S1到点P的波形图,其中初相ψ_1=π/2,波数k1=2π/λ1,sx为函数曲线的参数变量,其范围为[0,L],表示从双缝到光屏的距离;同理绘制从S2到点P的波形图,在命令栏输入:曲线((x(S_2)+sx, y(S_2)+tan(α_2) sx, A_2 cos(ψ_2-k_2 sx/cos(α_2)+ω_2 t)), sx, 0, L)．如图3所示．

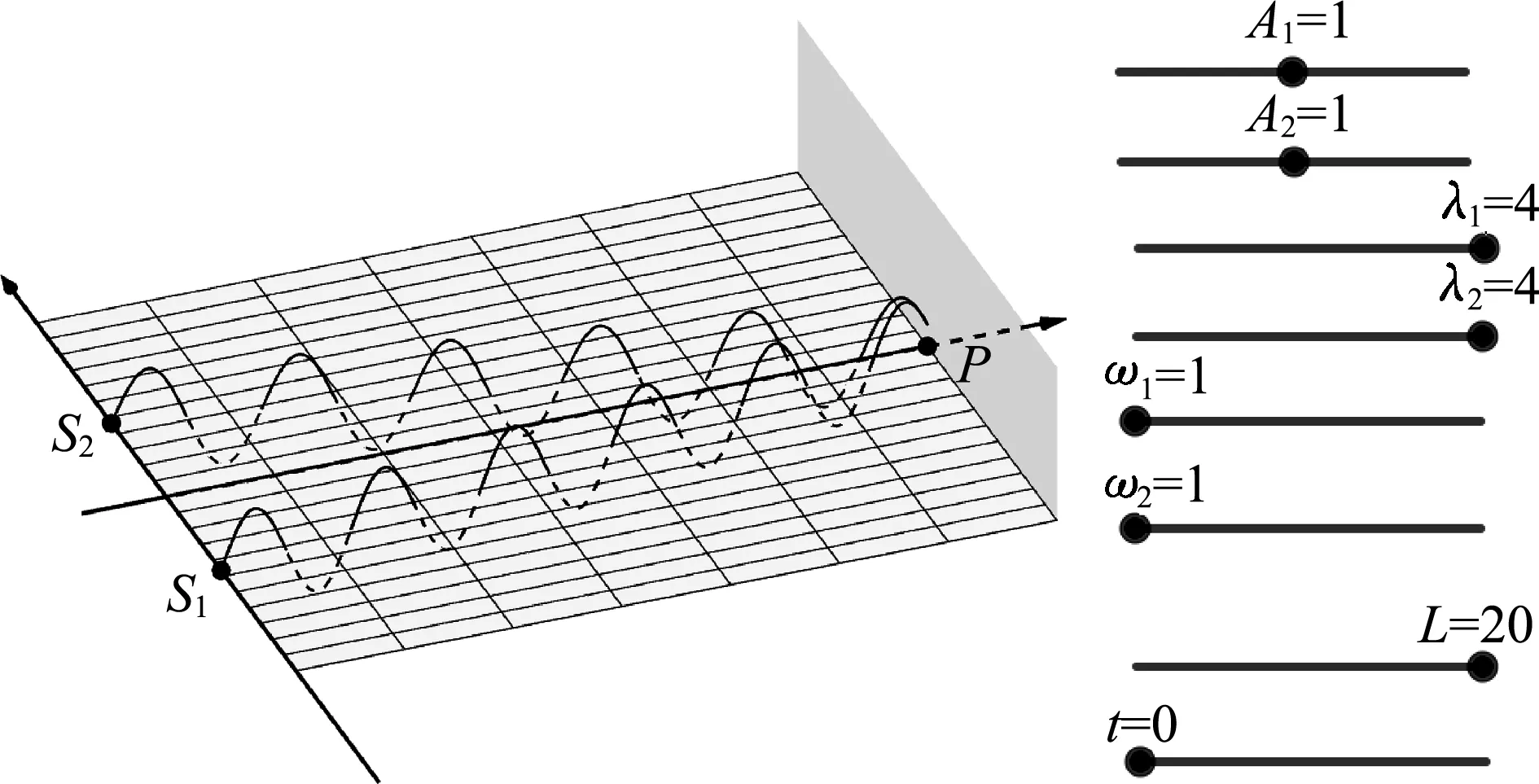
图3 相干光波的设定

(3) 绘制合振动图.

点P的振动由两列波叠加而成,只有明白点P的振动情况才能理解干涉的内涵,为了形象清晰描绘出三维视图中点P的振动情况,可以在过点P且平行于xOz平面绘制点P为振源的假想波,在命令栏输入:曲线((x(P)+sx, y(P), A_1 cos(ψ_1-k_1 (s_1+sx)+ω_1 t)+A_2cos(ψ_2-k_2 (s_2+sx)+ω_2 t)), sx, 0, λ_1),如图4所示,其中A_1 cos(ψ_1-k_1 (s_1+sx)+ω_1 t)+A_2 cos(ψ_2-k_2 (s_2+sx)+ω_2 t))表示两波的叠加,s1为线段S1P的长度,s2为线段S2P的长度．

(4) 呈现干涉图样.

① 为了研究干涉图样,着重研究了点P的振动情况．点P虽然可动但毕竟只是一点,而干涉图样是空间分布,为避免学生“只见树木不见森林”,可以在光屏上呈现干涉强度图像．在命令栏输入:s1(x)=sqrt((y(S_1)-x)2+L2),将以P点的y值作为参数代入函数,得到此时P点与S1点的距离,同理在命令栏输入:s2(x)=sqrt((y(S_2)-x)2+L2)得出,P点到S2点的距离．

② 在命令栏输入:曲线((x(P), sy, sqrt(A_12+A_22+2A_1 A_2 cos(ψ_2-ψ_1-(k_2 s2(sy)-k_1 s1(sy))))), sy,-20, 20),根据波的叠加规律得到点P在光屏的振幅分布,可以直观显示整体的干涉情况．最终效果如图4所示．

图4 假想波与光强曲线

3 GeoGebra课件优势与应用

(1) 以波动的形式展示光的传播与干涉.

光线是几何光学模型,具有简单形象的优点,可以充分阐述光的直线传播、反射与折射规律等．但用于解释光的波动性,光线模型变成缺点,过于简单而欠形象,忽视了波动特征．纵使学生已经学习了机械波的叠加与干涉,也别奢望学生经过一两节的学习就能深刻理解波动性,用光线模型示意波的传播过程实属操之过急,教材中说:“两列波的波峰与波峰叠加”,学生很纳闷:波峰在哪?根本原因在于教材编写时忽视光线模型的适切范围．

GeoGebra课件具有动态直观的特点,可以生动传神地展示光波的传播过程．右击时间t滑动条,启动动画,变量t在均匀“流动”,两列波从双缝徐徐向P点传播,拖动转换3D视角,学生可以从各个角度进行观察,切身体会光的传播过程,比教材的两条光线表示波的传播过程形象百倍．利用GeoGebra的动态性可以准确地展示光波的叠加过程,滚动鼠标放大课件聚焦于典型叠加位置,细致清晰展现叠加细节,为理解干涉打下基础．

① 干涉加强区域.

如图所示5,两列波在P点相遇,均处在波峰位置,随着时间的推移,两列波由波峰逐渐向波谷移动,二者始终保持同一步调,同时到达平衡位置、同时到达波谷、同时返回波峰位置,以点P为振源的假想波振幅变成S1、S2两列波的两倍,学生有充足的时间和空间体会“加强”的物理意义,容易理解为什么在此区域会出现亮条纹．课本图片加强区要么是显示波峰与波峰的叠加、要么是波谷与波谷的叠加,缺乏中间动态过程,常常误导学生:加强区质点的位移一直处在最大位移处,位移不可能为0．而利用GeoGebra课件动态演示可以有效防止出现诸如此类的错误认识．

② 干涉减弱区域.

如图所示6,两列波在P点相遇,波1处在波峰位置,波2处在波谷位置,随着时间的推移,二者始终保持相反步调,两列波的振动在P点完全抵消,以质点P为振源的假想波变成了一条直线,所以此处的P点呈现暗条纹．学生经常错误地认为减弱区振幅一定为0,这与课本所举事例皆为等振幅波源有关．调节GeoGebra课件中振幅滑动条,使波1和波2 的振幅不再相等,从课件可以直观看出P点振幅不为0;也有学生认为P点振动一定比两列波中的任何一列波振动都弱,同理调节GeoGebra课件振幅滑动条,使A2A2,从课件可以直观看出P点振幅大于波2的振幅,从而纠正学生的错误认识．

图6 相消干涉

③ 干涉一般区域.

课本用干涉最强区代替加强区,用干涉最弱区代替减弱区,忽略中间的一般过渡区域,导致学生认为干涉要么是最强的要么是最弱的,中间存在明确的界限．在GeoGebra课件中,拖动P点改变其位置,从干涉最强点到最弱点缓慢移动,使学生感受到振动强度的连续变化,通过光强曲线直观表达振幅在光屏的变化,让学生深刻理解明暗的渐次演变．

(2) 动态展示空间干涉.

“光的干涉高端备课”一文指出“教材一开始就引入了光的双缝干涉实验,在暗室中用氦氖激光器发出的红色激光照射金属挡板上的两条平行狭缝,学生可以在屏上观察到明暗相间的干涉条纹,由于该实验仅在固定的光屏上进行观察,会让学生误以为干涉只发生在光屏处,如凸透镜只有光屏处成一个清晰的像一样”．教材在处理光的空间干涉问题确实存在不足,容易误导学生只有在光屏处才有干涉现象产生．通过慢慢拖动滑动条L,改变光屏与双缝之间的距离,可以观察到振幅曲线依然存在,改变GeoGebra课件视角,从多个角度观察振幅曲线,体现空间干涉．引导学生观察到振幅曲线的间距——条纹间距——是否发生变化及如何变化,让学生猜测影响条纹间距的其他因素,顺利过渡到研究“决定条纹间距的因素”．

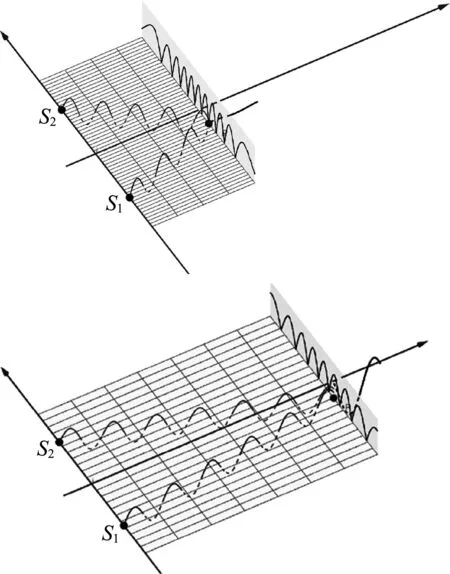
图7 条纹间距与双缝到屏之间距离的关系

(3) 直观显示决定条纹间距的因素.

本节教材第2部分小标题是“决定条纹间距的因素”,但第2部分内容只讲了产生亮纹和暗纹的条件,绝口未谈“决定因素”,让人匪夷所思．教材下一节内容是“实验:用双缝干涉测量光的波长”,首先推导了决定条纹间距的公式,然后利用此公式测量光的波长,学生会感到很突兀:怎么会想到通过测量条纹间距来测量波长的呢?如果在两节内容之间衔接一个真正的“决定条纹间距的因素”,通过定性研究波长与条纹间距的关系,学生便会觉得通过条纹间距测量波长顺理成章．在展示干涉空间性时,得到距离越大,条纹间距越大,如图6所示．影响条纹间距还有哪些因素呢?改变入射光的波长,即拖动λ滑动条,可以发现,波长越长,条纹间距越大;改变双缝之间的距离,即拖动点S2,可以发现,S1、S2距离越小,条纹间距越大．有此作为基础,对条纹公式x=Lλ/d会有更加深刻的理解．

4 小结

本文通过GeoGebra的3D视图,动态地展示了光波的传播过程,鲜活地呈现光的叠加过程,有效防止学生错误认识倾向,使学生真正理解干涉机制,深入理解光的波动特性．