基于认知发展机制的过程设计
——以“胡克定律”为例
2018-08-24徐将二
徐将二
(浙江省诸暨市第二高级中学,浙江 诸暨 311800)
从课程标准看,课标要求从学生熟悉的现象引入内容,通过实验探究弹簧弹力与伸长量的定量关系,进而比较深刻地理解胡克定律.从教材内容看,人教版教材以通俗的语言、直观的图像、简短的篇幅讲述了胡克定律的获得过程.从已有认知看,学生知道了在外力作用下产生了形变、在形变作用下产生了弹力,明白了弹簧弹力与伸长量的定性关系,学会了使用弹簧测力计的方法.虽然很多教师都知晓课标要求、教材安排、学生认知的这3方面内容,但在实际教学过程设计中,还是出现了诸多问题.有鉴于此,必须对“胡克定律”的教学过程重新进行设计,以期对规律教学的改进有所裨益.
1 传统过程设计及其问题
传统过程设计主要由3个循序渐进、环环相扣的步骤组成.第1步引入规律,首先通过演示海绵的受压来说明形变越大,弹力也越大(如图1所示),然而海绵产生的弹力与形变的定量关系比较复杂,因此研究最简单的情况——弹簧的弹力与伸长量之间的定量关系;接着通过如图2所示[1]的演示实验启发学生去猜测弹簧的弹力与伸长量之间的关系;然后提炼学生的猜想.

图1
图2

图3
第2步探究规律,让学生根据如图3所示的装置去进行实验,将学生分成若干组,不同组使用相同规格的弹簧(J2110螺旋弹簧组中的“5 N”型弹簧).其中1组实验数据如表1所示,根据数据作出弹力与伸长量关系的F-x图像(如图4所示),图像是一条不过原点的直线,在误差允许范围内F与x成正比(F=kx),从而验证猜想并获得胡克定律.
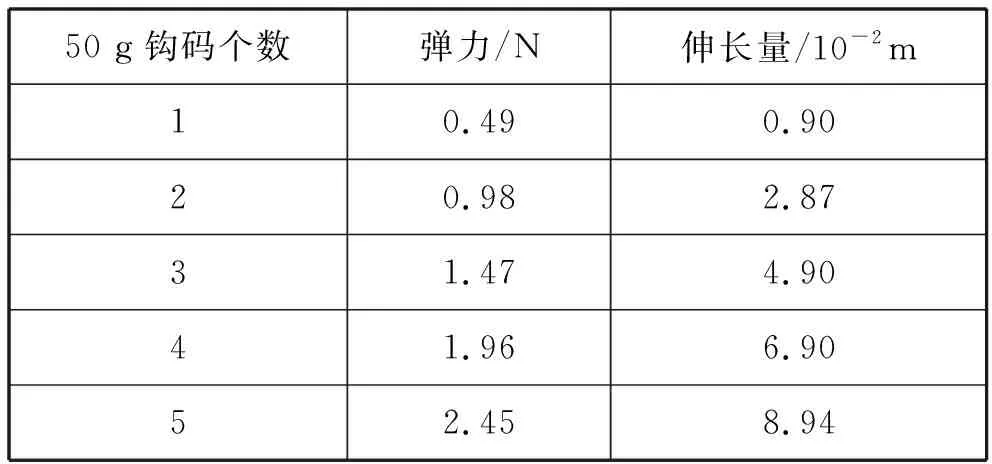
表1
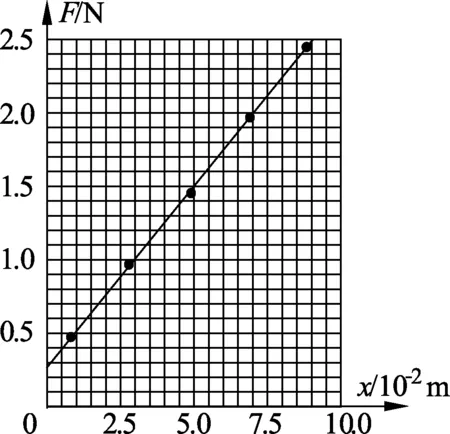
图4
第3步运用规律,经常采用如下的经典习题:有一弹簧,当挂上2 N的钩码时,长为11 cm;当挂上4 N的钩码时,弹簧再伸长2 cm,求弹簧的劲度系数.
综观上述过程设计,发现存在以下几个方面的问题: (1) 教材使用教条化.图2中一个弹簧水平放置处于自由状态,同时用手拉另2个弹簧使其水平伸长一定的长度,这样的操作比较麻烦.手拉弹簧的力是任意的,学生不容易猜想出弹簧弹力与伸长量之间的关系,导致猜想的指向性不明确.整个装置放置在水平面上,不利于学生的观察.这些负面影响实际上是由于教师把教材当作“圣经”,照搬照抄教材内容所致,其实教材为教师的教学过程设计指明了一个方向、提供了一个思路,教师应该根据教学实际情况用“教材”教,而不是教“教材”.(2) 结论获取理想化.根据表1中数据作出的F-x图像为什么是一条不过原点的“理想”直线而不是一条曲线?到底是什么样的误差造成图像中的“理想”直线会变成更“理想”的正比例关系?为什么探究规律的过程会这样“理想化”处理?究其原因,教师心中的“理想化”教学模式在作祟,导致对数据的处理、图像的分析、规律的获取没有符合实际情况.(3) 规律应用片面化.所谓的经典习题没有真实的情境作为依托,与实际生活是脱离的,它偏重于生搬硬套规律、机械使用公式,实质是一种纯数学公式的推理验算来代替规律的实际应用,对学生科学思维的提升是毫无益处的.
2 基于认知发展机制的过程设计
规律教学的成败,往往并不取决于教师向学生传授正确的规律,而决定于学生的“准规律”是否向“科学规律”转变.皮亚杰认为认知发展得以发生的主要机制是平衡,平衡可以通过同化与顺应两种过程获得.[2]因此必须引导学生首先进行初步的观察与思考建立“平衡”、形成“准规律”;接着进行深入的观察与思考,经过交流、讨论、质疑,经历“失衡”过程,再获“平衡”,形成“新规律”;然后经历“新”观察与思考,打破原有“平衡”和认知方式,形成“新平衡”,建立“科学规律”.在经历过“失衡”向“平衡”转化的过程、“准思维”向“科学思维”发展的过程,学生的认知才有可能得以发展与深化,才有可能避免出现传统过程设计所形成的问题.
2.1 架设“桥梁” 建立“平衡”
为了使学生的认知更好地发展,可以在认知的“最近发展区”创设问题情境,一方面可以激活学生的原有认识、经验、观念,另一方面作为学习的“桥梁”,可以关联沟通新知识与旧知识,将新知识纳入原有认知结构,导致认知结构发生“同化”,促使学生的认知处于暂时的稳定平衡状态.因此在实际教学中可以采用如下的过程设计.
首先让学生体验塑料直尺被弯曲实验,亲身感受形变越大,弹力也越大(如图5所示).接着教师提出两个问题:直尺产生的弹力与形变的定量关系容易研究吗?哪种实验器材更容易研究弹力与形变的定量关系?学生容易获得答案:由于难以量化“力”与“形变”,即使量化了可能两者的关系也比较复杂,因此不容易研究;弹簧的弹力可以用钩码的重力来替代,弹簧的伸长量可以用直尺来测量,因此可以用最简单的弹簧来研究弹力与伸长量之间的定量关系.然后教师设置如图6所示的演示实验:将相同的5个强磁挂钩相隔10 cm吸附在磁性黑板同一水平线上,再取5个相同的J2110螺旋弹簧组中的“5 N”型弹簧挂在挂钩上面,从左向右在弹簧下端挂上0、1、2、3、4个50 g的钩码.教师引导学生猜想弹簧弹力与伸长量之间的定量关系:由于弹簧在水平方向是等间距放置,弹簧所挂钩码的个数以等差数列增加的,所以水平方向可以表示弹力大小;假如以第一个弹簧下端为原点,那么向下方向就可以来表示弹簧的伸长量.学生发现弹簧的下端似乎处于同一倾斜直线上,那么可得弹簧弹力与伸长量可能成正比例关系.

图5 图6
上述第1个实验相对于海绵受压演示实验,不但取材更加容易,而且学生亲身体验的感觉更加强烈,利于调动学生的学习兴趣;第2个实验在竖直平面上演示,利于观察、便于操作,避免了在水平面上操作的不利影响.这两个“台阶型”演示实验,从定性到半定量化,为学生进行科学合理的猜想提供了真实有效的依据,为学生原有认知(两个变量成单调递增关系)向新认知(两个变量成正比关系)发展与进化搭设了“脚手架”,为学生建立“平衡”奠定了认知基础.
2.2 引发“冲突” 获得“平衡”
在学生同化新知暂获平衡后,应当创设矛盾情境引发认知冲突,打破原有“平衡”,积极引导学生的认知状态向“顺应”转变,主动修改原有认知结构,建立新的认知结构并获得新的“平衡”,从而实现认知结构的深化与发展.因此在具体教学操作中可以采用如下的过程设计.

图7
第一步,首先根据如图7所示的装置(图中弹簧为J2110螺旋弹簧组中的“5 N”型弹簧),由教师完成相关实验,得到的1组实验数据如表2所示,接着让学生根据数据作出弹力与伸长量关系的F-x图像,学生得到的图像如图8所示,此时学生感到很困惑.
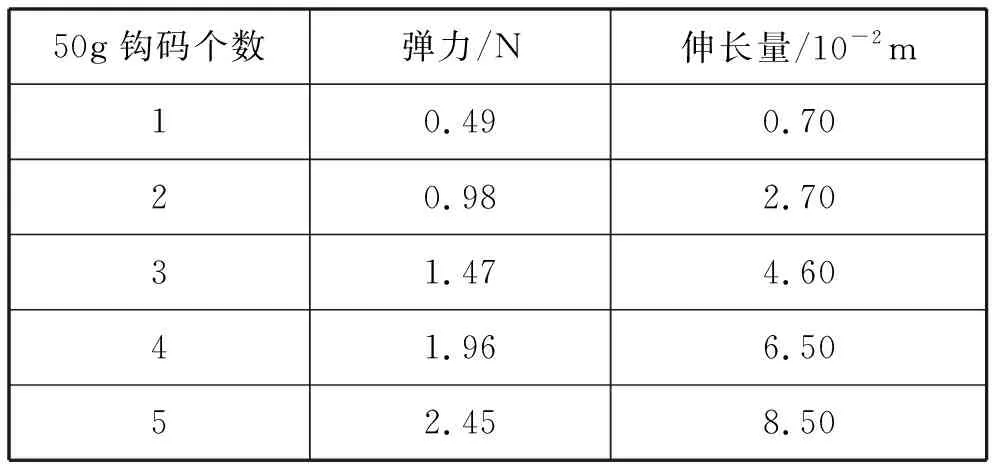
表2
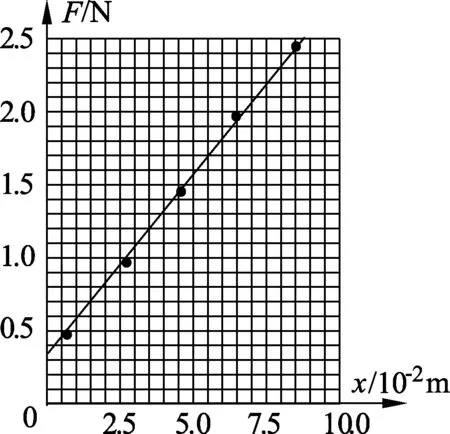
图8
为什么根据数据作出的图像不是一条过原点的直线?图像是否正确?然后教师顺着学生的疑问,指出问题的焦点在于图像的开始阶段应该多收集些数据,才能解决学生的疑惑.最后,教师再次进行实验,得到的数据如表3中第3列所示,从而可以得到如图9所示的图像(图线前面部分为曲线,后面部分为直线).这个结论与学生原有认知产生了激烈的冲突,主要体现在两个方面:一是图像是曲线而非过原点的直线,二是悬挂10 g钩码时弹簧伸长量竟为0.

表3

图9
第二步,学生自主探究J2110螺旋弹簧组中的“3 N”型、“2 N”型弹簧的弹力与伸长量之间的关系,教师可以将学生分成若干组,每组选用的装置如图7所示,图中弹簧换成“3 N”型与“2 N”型,提供的钩码有10 g,20 g,50 g,200 g 4个种类.学生根据在第一步中获得的“经验”,模仿上述实验操作,获得了“3 N”型和“2 N”型弹簧的相应数据(如表3中第4、5列所示)及相应的F-x图像(如图10、11所示).
第三步,首先教师将3种类型弹簧的F-x图像集合在一起进行比较,让学生观察图像发现其中的特点:3种类型弹簧的图线前面部分为曲线,后面部分为直线,但“5 N”型弹簧图线前面部分弯曲最明显且不过原点,“2 N”型弹簧图线前面部分几乎没有弯曲且几乎过原点.接着让学生猜测图像形成的原因:弹簧自身的因素造成的,比如弹簧粗细、软硬、大小、匝数、质量等等.然后让学生思考从“5 N”型到“2 N”型弹簧,弹簧的粗细、质量等因素逐渐变小,其图线形状越来越趋向于过原点的直线,那么弹簧自身因素一切理想化后,它的图线应该是怎样的?学生容易获得结论:理想弹簧的F-x图像是一条过原点的直线.最后师生一起归纳总结胡克定律,弄清楚它的内涵.

图10
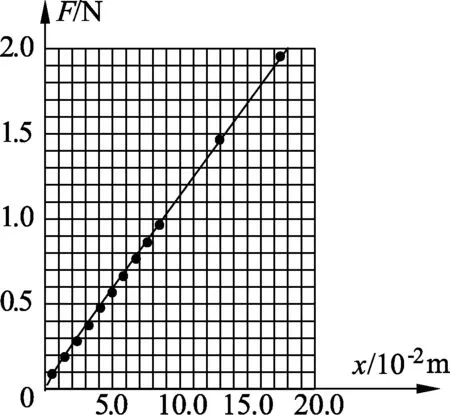
图11
上述3个步骤中,第一步侧重于在实验情境中引发认知冲突,导致学生的认知处于失衡状态,为改变原有认知寻求新的平衡状态奠定了基础.第二步的自主探究过程强化了新认知,促进了认知结构的转变,使新平衡趋于稳定状态,使新认知得到了发展与深化,也为二次转变准备了条件.第三步中通过极限思想与理想化方法处理研究对象,使顺应过程得以顺利进行,学生的认知再次发生转变,重新获得稳定的认知平衡状态.
2.3 应用“新知” 形成“平衡”

图12
学生获得新知识后,需要设置新情境,让学生自主探究情境中的新问题,运用方法与策略解决新矛盾,促使同化与顺应过程的再次发生,实现认知结构的再次转变与发展,形成新的认知平衡状态.因此在应用新知识中可以采用如下的过程设计.
首先由教师安排好各种器材:镀锌铁丝弹簧(直径为2 mm、匝数为10匝、外径110 mm、螺距35 mm),50 g钩码若干个,1 m长直尺,铁架台一个.接着将学生分成若干组探究弹簧弹力与伸长量的关系,学生设计的实验装置如图12所示,获得的实验数据如表4所示,作出的F-x图像如图13所示,图线前面部分是直线,后面部分是曲线,图线与学生原有认知既有相容的地方——直线符合胡克定律,又有矛盾的地方——曲线不符合胡克定律.然后,师生共同解决矛盾与问题:前面直线部分弹簧没有超过弹性限度符合胡克定律,后面曲线部分超过弹性限度胡克定律不再适用.
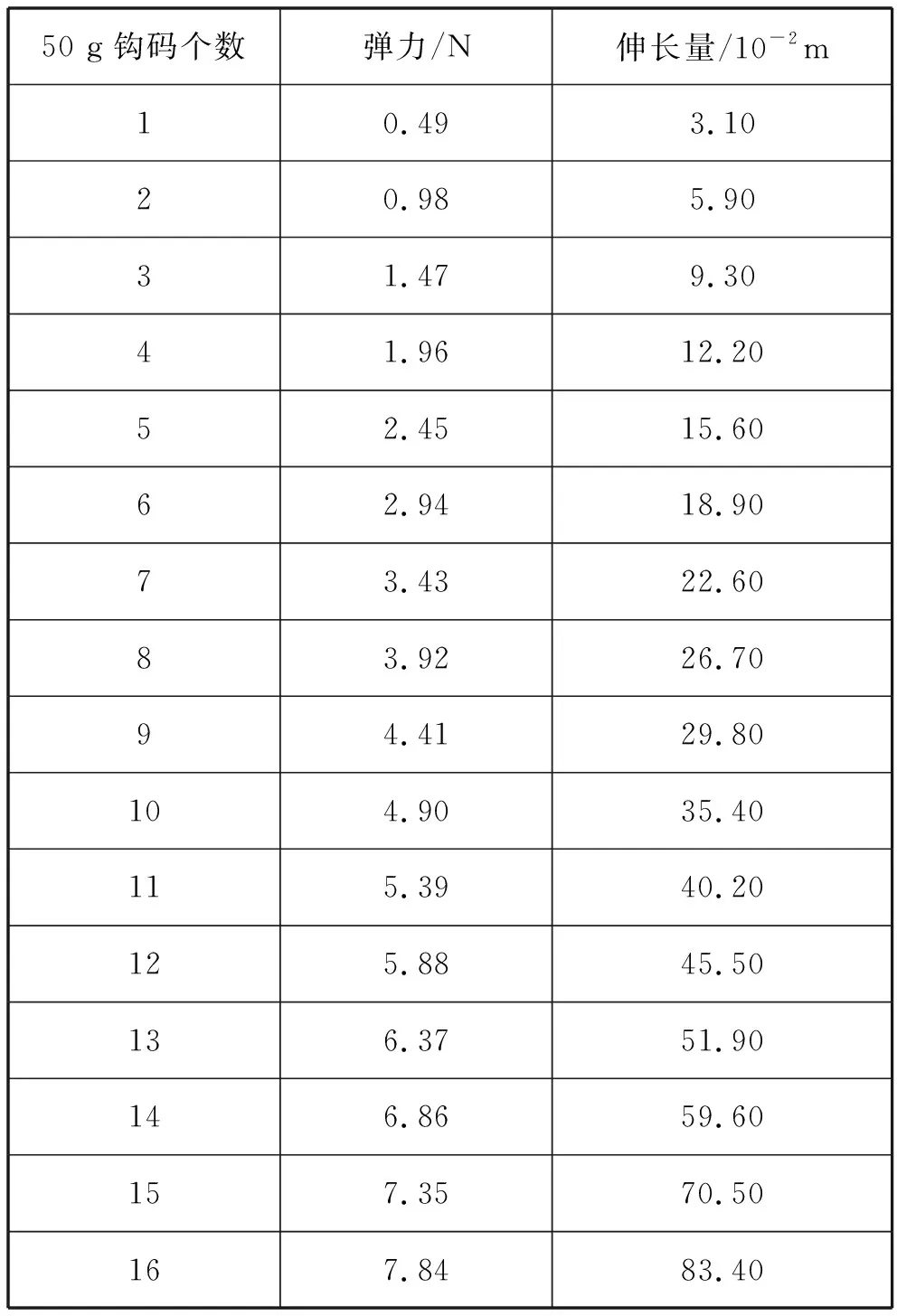
表4
上述过程设计的优点主要体现在以下3个方面: (1) 镀锌铁丝弹簧比J2110螺旋弹簧容易演示超过弹性限度的情况,并且容易恢复原状,利于学生观察与操作; (2) 学生通过设计实验装置、进行实验探究、获得实验结论,掌握了科学探究的方法,提升了科学思维的能力; (3) 学生在作出图线、分析成因的过程中,促进了认知结构的再次同化与顺应,促进了稳定平衡状态的形成.

图13
3 规律教学过程设计的启示
依据上述过程设计,可以得到以下3点启示.
(1) 以科学探究为手段.
“科学探究”是指提出科学问题、形成猜想和假设、设计实验与制订方案、获取和处理信息、基于证据得出结论并作出解释,以及对科学探究过程和结果进行交流、评估、反思的能力.[3]因此在规律教学过程设计中,必须以科学探究为手段,通过科学探究来学习科学知识与方法、提高实验素养、提升问题解决能力、发展科学思维、养成科学态度与责任.
(2) 以科学思维为重点.
“科学思维”主要指高中物理中重要的思维方法,包括建模的思想、理想化方法、分析综合、抽象概括、批判性思维、推理论证等思维与方法.[4]因此在规律教学过程设计中,必须以科学思维为重点,展现学生的思维过程、揭示学生的思维特征、提升学生的思维能力与品质.
(3) 以认知发展为中心.
学生习惯于原有认知结构去解释问题,一旦原有认知结构与新事实产生冲突,就会出现认知不平衡状态,教师应当引导学生,通过同化与顺应机制去克服认知不平衡而达到稳定的“新”平衡状态,从而使认知得到发展与深化.因此在规律教学过程设计中,必须以认知发展为中心,通过铺设台阶与引发矛盾等策略,促使“准认知”向“科学认知”转化.
