非线性波动Zakharov方程组的多辛Fourier拟谱算法

张 星 单双荣 徐金平

（1.福建生物工程职业技术学院公共基础部，福建 福州 350002；2.华侨大学数学科学学院，福建 泉州 362021；3.闽南理工学院，福建 石狮 362021）

1.引言

文章考虑如下非线性Klein-Gordon-Zakharov（简称KGZ）方程组

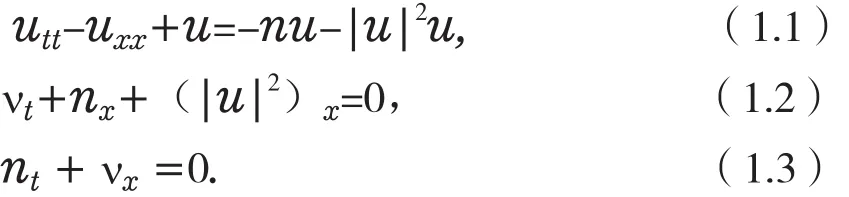
是描述在等离子体中Langmuir波与离子声波交互作用的一个经典模型。［1］在数学上，该方程表现为含有两个未知函数u（x，t）和n（x，t）的耦合方组。其中u（x，t）是复函数，而n（x，t）则是实函数。

文章在xL≤x≤xR，0≤t≤T上对带有如下初边值条件

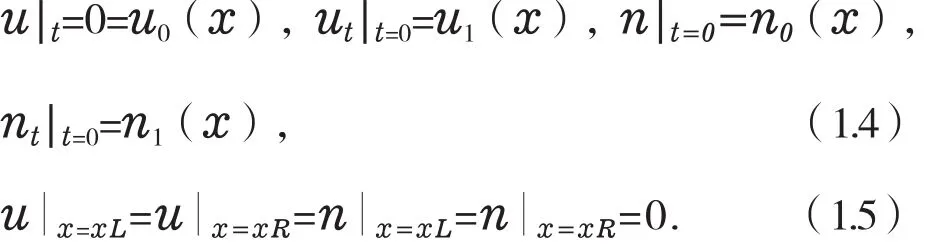
的一维KGZ方程从辛几何的角度去考虑，其中函数u（x，t）为复值函数，函数n（x，t）为实值函数，u0（x），n0（x），u1（x），n1（x），均为已知函数。先把方程组引入正则动量转化成多辛形式的方程组，再对得到的多辛方程组用Fourier拟谱方法离散，可以得到其多辛Fourier拟谱格式，最后通过数值试验验证多辛Fourier拟谱格式（3.2.3）满足二阶精度0（h2+τ2），并且能长时间保持孤立波传播。

2.非线性KGZ方程组的多辛形式及其守恒律

利用方程（1.2）和（1.3），可以消去ν（x，t）得到下面的方程组

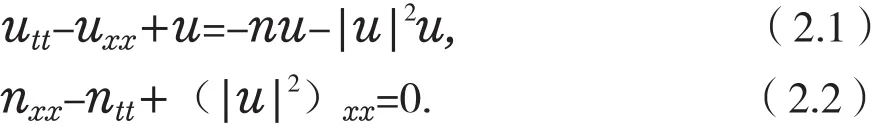
下面考虑KGZ方程组（2.1），（2.2）的多辛结构及其相关守恒律。

令u（x，t）=P（x，t）+iq（x，t），则方程组（2. 1），（2. 2）可化为

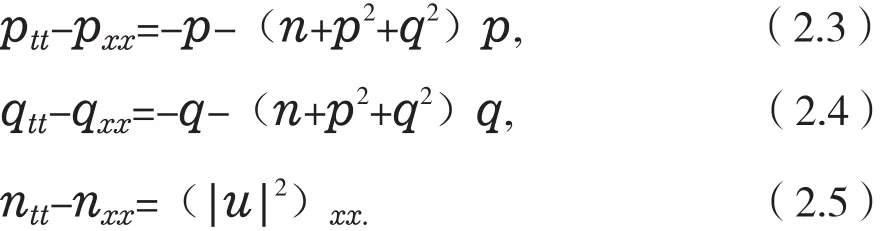
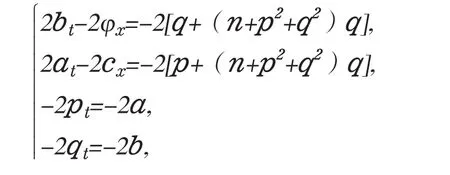
引入正则动量pt=a，qt=b，px=c，qx=φ，nt=νx，wx=ν.得到KGZ方程组（2. 1），（2. 2）的多辛方程组在不同时刻的孤立波的传播情况，图5和图6分别给出|u|和n在步长（h，τ）=（0.05，0.01）时多辛Fourier拟谱格式得到的孤立波模拟，多辛Fourier拟谱格式能很好的模拟孤立波的传播。

图3和图4分别给出|u|和n在不同时刻的孤立波的传播情况

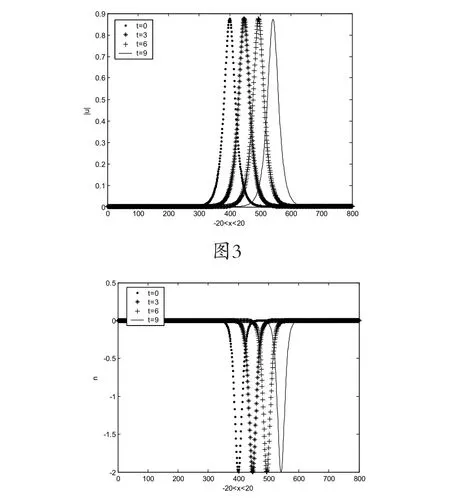
图4

图5 和图6分别给出|u|和n在步长（h，τ）=（0.05，0.01）时的孤立波模拟

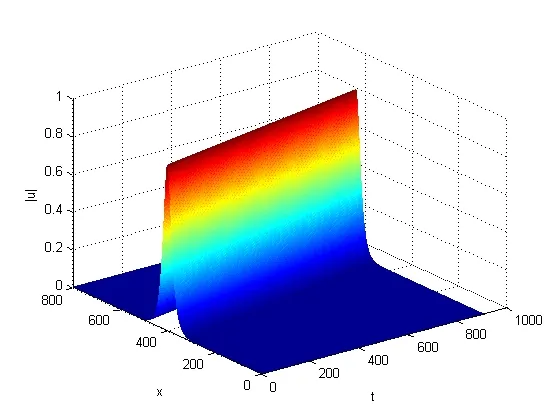
图5

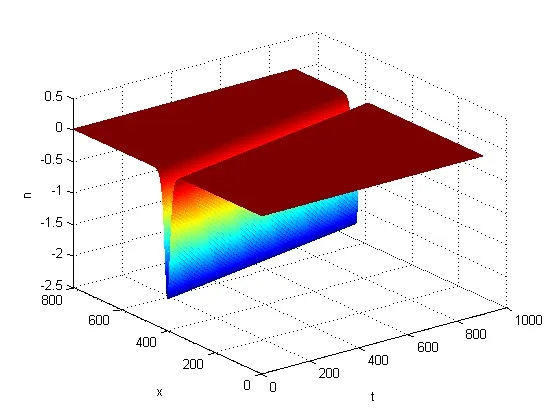
图6

综上数值实验由表1-表3，图1-图6可以看出：

（1）通过多辛Fourier拟谱格式（3.2.3）计算出的数值解很好的逼近了精确解，并且满足二阶收敛性。

（2）多辛Fourier拟谱格式（3.2.3）能够长时间的模拟孤立波.经过了长时间的数值模拟后波的各个要素，如：形状、振幅等，能够很好的保持，长时间误差较小。

（3）多辛Fourier拟谱格式（3.2.3）在不同网格比下，能够很好的模拟孤立波的传播。

由此验证了文章构造的多辛Fourier拟谱格式（3.2.3）是正确有效的。