基于匹配滤波的高效干扰感知方法

逄天洋，李永贵，牛英滔，韩 晨，夏 志

(1.陆军工程大学， 江苏 南京210000；2.南京电讯技术研究所，江苏 南京 210000)

0 引言

在信息化战争中，恶意干扰已成为军事无线通信的主要威胁[1]。随着干扰技术的不断发展，干扰样式已从传统的阻塞式干扰发展为效率更高、作用范围更广、攻击性更强的智能干扰[2]。完备的智能干扰机从战术目标出发，通过侦察、学习和推理，采取最优干扰策略，同时能够根据反馈的干扰效果实时调整干扰策略，从而达到高效干扰的目的。因此，智能干扰已成为军事无线通信系统面临的严峻挑战，亟待深入研究并提出有效应对的方法。

文献[3]提出了一种基于数字调制系统的最优干扰波形，文中从以误码率最高为优化准则，利用全局最优解和局部最优解的数学方法求解满足优化准则的干扰波形。这种最优干扰针对不同的通信信号调制方式发出不同的干扰波形，且干扰波形与通信波形具有高相关性。与传统的高斯噪声干扰相比，这种干扰实现了高信噪比下的高误码率，是一种典型的物理层智能干扰[4]。本文以这种干扰作为研究对象，研究其感知方法。

文献[5]提出了基于循环平稳特性的信干噪比估计方法，能够较准确地估计出在高斯信道和瑞利信道下的信干噪比，可为干扰检测提供重要依据。但该方法要求干扰信号与通信信号是独立统计的。文献[6]从干扰信号的高阶累积量中提取特征参数用作支持向量机分类的特征向量，从而识别干扰信号的调制方式，但不足之处在于此算法需事先利用盲源分离技术将混合信号中的干扰信号分离出来；并且文中的干扰样式是噪声干扰、单音干扰等传统干扰样式。文献[7]提出了基于高阶累积量和循环谱的调制方式识别方法，可识别多种调制方式，但不足在于其只能对信道内单一信号进行识别，难以对混合信号进行区分并识别。文献[8]通过盲源分离技术对同频混合信号进行区分并识别，但需要先验信息作为基础，且算法复杂度较高。文献[9]利用四阶累积量对单一信道混合的两个信号进行调制方式识别，但是前提是保证通信信号与干扰信号的统计独立。文献[10-16]均是利用能量检测法或循环平稳特性进行干扰信号或可用频谱检测，但文献所涉及的干扰信号均为噪声干扰，并没有关于高效干扰的检测方法。综上所述，当前已有文献主要存在干扰样式单一、仅能对单信道内单一信号调制方式识别的问题，难以满足本文中与通信信号具有高相关性的干扰信号的识别。因此，本文主要研究存在通信信号时最优干扰信号的感知问题。

1 系统模型

1.1 最优干扰模型

由文献[3]可知，高斯信道中存在干扰时的M-QAM信号的平均误码率为：

(1)

式中，l为干扰信号，SNR为信噪比，JNR为干噪比，M为星座图的阶数，dmin为当前调制方式下的最小欧氏距离。最优干扰的数学表达式就是计算式(1)最大时l的分布。

(2)

式中，a为干扰信号l的幅值。文献[1]已证明，在一定的干信比条件下对于M-QAM信号最优干扰波形的调制方式是随着信号调制方式变化的。为便于讨论与研究，本文采用的通信信号调制方式为16QAM。根据文献[1]中的结论可知，此种通信信号对应的最优干扰波形为QPSK调制干扰波形。

1.2 接收机模型

为方便研究，本文采取如下假设：

① 信道中存在零均值高斯白噪声，且与通信信号和干扰信号之间是独立的；② 干扰信号与通信信号是同步的，其他信息是未知的；③ 同一信道中除通信信号外，只存在一种调制方式的干扰信号；④ 本文可能的干扰信号调制方式集合为{BPSK，QPSK，8PSK}；⑤ 通信信号的调制方式为16QAM。

由于通信信号与干扰信号都经过调制，因此到达接收机的信号是由多种调制信号混合而成的，单信道中多个线性调制信号混合的信号数学模型[17]可表示为：

y(t)=s(t)+l(t)+n(t)，

(3)

式中，s(t)为信道内经调制后的通信信号，l(t)为同一信道内的干扰信号，n(t)为加性噪声。由文献[1]可知，此时的最优干扰信号的调制方式为QPSK。16QAM和QPSK可分别表示为：

xQPSK(t)=cos(2πfct+θm)m=1,2,3,4，

(4)

x16QAM(t)=rncos(2πfct+θn)n=1…16，

(5)

式中，fc为载频，θ为载波相位，r为幅度，m,n为调制方式的阶数。由于接收信号中的通信信号调制方式已知为16QAM，故干扰感知问题可简化为检测某一通信信道中是否存在QPSK调制的干扰信号。通过以上模型和假设，本文要研究的问题是：在最优干扰与通信信号的混合信号中，如何感知最优干扰信号的存在。

2 算法描述

由文献[18]给出的结论可知匹配滤波器的冲激响应为：

h(t)=kxm*(t0-t)，

(6)

H(f)=S*(f)e-j2πfT，

(7)

式中，k为任意常数，xm(t)为干扰信号时域表达式，t0为时延，H(f)为滤波器频率响应，S(f)为xm(t)的傅里叶变换。由上式可知匹配滤波器的冲激响应就是延时的信号xm(t)的镜像。匹配滤波器无论是从时域还是从频域，都充分保证了所匹配的信号尽可能多地通过，噪声或其他信号尽可能少地通过，因此能获得最大信噪比输出。

由匹配滤波原理可知，与匹配滤波器匹配的信号，在经过匹配滤波后会形成幅度较高的输出。因此利用此原理可以检测本文中的混合信号中干扰信号的调制方式。

将信号y(t)作为匹配滤波器的输入，算法原理如图1所示。

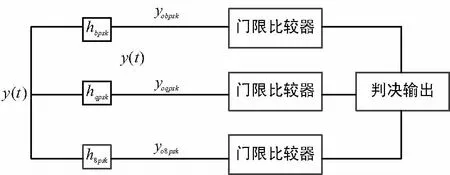
图1 检测流程

滤波器的冲激响应由式(6)得到，本文为方便计算取k=1,t0=0，则各匹配滤波器的冲激响应为：

hBPSK(t)=xBPSK*(-t)=cos(-ωt+θm)m=1,2，

(8)

hQPSK(t)=xQPSK*(-t)=cos(-ωt+θm)m=1,2,3,4，

(9)

h8PSK(t)=x8PSK*(-t)=cos(-ωt+θm)m=1,2…8。

(10)

匹配滤波器的输入信号y(t)为：

y(t)=axm(t)+bx16QAM(t),

(11)

式中，a,b分别为xm(t),x16QAM(t)的幅值，用以确定滤波器输入的信干比。为方便公式计算，此计算式中不考虑噪声的存在。将式(10)整理得：

y(t)=Acos2πfct-Bsin2πfct，

(12)

式中，A=acosθm+brncosθn;B=asinθm+brnsinθn;θm为干扰信号调制方式的不同相位，m=1，2，3，4;rn,θn为16QAM调制的不同幅值和相位，n=1…16。

将混合信号y(t)输入匹配滤波器，则各匹配滤波器的输出为：

(AsinθJ+BcosθJ)sin2πfct]+T[(AcosθJ-BsinθJ)·

cos2πfct+(AsinθJ-BcosθJ)sin2πfct]，

(13)

式中，J=BPSK,QPSK,8PSKT为符号周期，θJ为不同干扰方式对应的不同相位。

当干信比足够大时，A≈acosθm、B≈asinθm，则式(13)可简化为：

(14)

由上式可得到，匹配滤波器输出的幅值大小仅与干扰信号的相位与幅值有关。且当匹配滤波器冲激响应的相位与输入信号的相位相匹配时取得最大值：

yoJmax(t)=max(yoJ(t))，当且仅当θJ=θm。

(15)

式(13)表明，当混合信号中存在于匹配滤波器冲激响应相匹配的信号时，滤波器的输出会有较高的幅值。

3 仿真验证

仿真中设定采样频率为10 MHz，通信信号与干扰信号的载波频率均为1 MHz，仿真时间为10-4s。通信信号为16QAM信号，滤波器分别为BPSK，QPSK，8PSK滤波器，干扰信号为QPSK信号，且仅在10-5～2×10-5s实施干扰，干信比为15～0 dB(文献[1]中提到的干信比的拐点，在此干信比范围内，最优干扰为QPSK调制信号)。

设匹配滤波器的输入为x[n]，n为仿真中设定的点数，则有：

∑x[n]y[n]>λ，

(16)

式中，y[n]为匹配滤波器的冲激响应序列，λ为不同滤波器的判决门限值，门限值在仿真中设定为除去当前滤波器外的其他两个滤波器输出的最大值。

图2为干信比为3 dB、信噪比为5 dB时，各滤波器的输出幅度。由仿真图可以看出，3种滤波器在干扰存在的时刻都发生了较大的响应，均在干扰出现时刻产生了相关峰。这是因为本文预先设置的干扰信号集(BPSK,QPSK,8PSK)的时域波形均有不同程度的相关性，因此造成了混合信号通过3种滤波器时，产生了形状类似、幅值不同的相关峰。但是QPSK滤波器的相关峰超过了判决器的门限，根据式(13)可以得到此干扰信号的调制方式为QPSK。

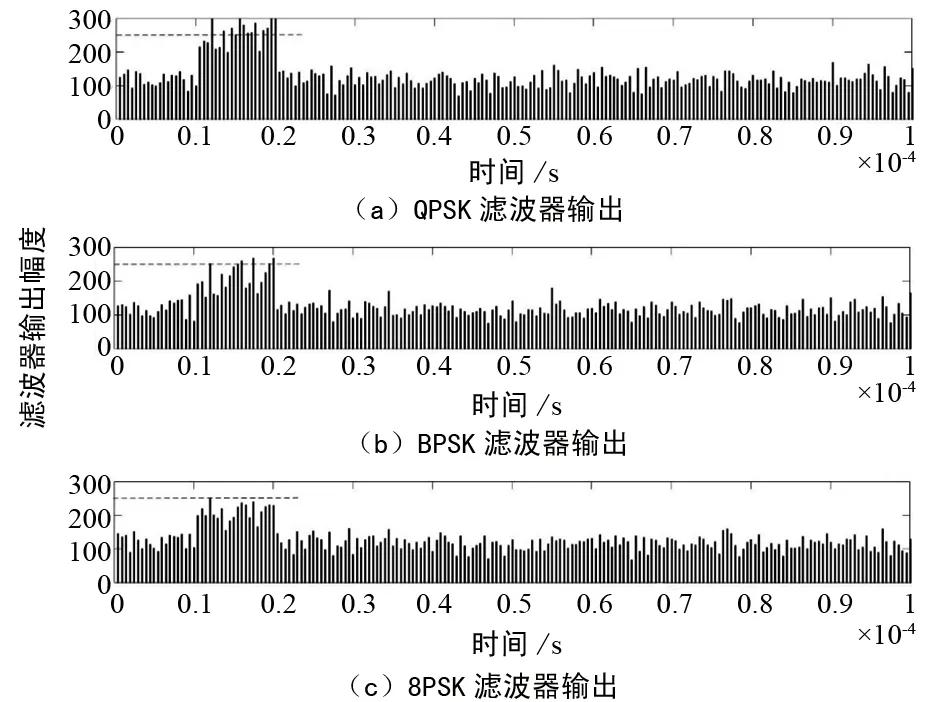
图2 滤波器输出

图3为不同干信比条件下最优干扰的检测概率。为方便计算，仿真中取50个采样点为一组进行平均能量的计算，将此平均能量与门限值进行比较来确定干扰信号的存在。门限值通常是根据经验值得到的，本仿真中将门限值设定为特定干信比条件下BPSK、8PSK滤波器响应峰值的最大值，以确保门限判决器的判决结果不会受其他2个滤波器的影响。由图3可知，检测器的检测概率随着干扰信号功率的增强而增大。干扰信号的功率增大，相应的滤波器的响应也会增大，相反其他2种滤波器的响应并不会有明显增强，因此与QPSK滤波器的响应差值会逐渐变大，使得检测器的检测概率增大。

图3 干扰检测概率与干信比的关系

4 结束语

从已有文献提出的最优干扰模型出发，研究了此种干扰的检测策略。由于这种干扰是根据不同调制方式的通信系统发出不同调制方式的干扰信号，干扰信号与通信信号的调制方式具有高相关性，因此将这种最优干扰的检测策略作为智能干扰检测的一种研究案例。提出了基于匹配滤波器的部分最优干扰检测模型，主要利用匹配滤波中相同信号的相关峰值最大的思想，检测单信道中混合调制方式的识别，以此达到检测部分最优干扰的目的。仿真实验结果证明，本文提出的算法在一定条件下能够准确检测出最优干扰的存在，并且在干信比超过14 dB时，检测概率可趋近于100%。