Doherty功放的贝叶斯正则化神经网络逆向建模研究

南敬昌，胡婷婷，盛爽爽，高明明

(辽宁工程技术大学电子与信息工程学院，辽宁 葫芦岛 125105)

1 引言

随着无线通信系统的快速发展，射频微波电路变得越来越重要，但使用ADS(Advanced Design System)软件辅助设计微波电路需要花费大量的时间且设计步骤繁琐，实现困难。为了简化设计步骤、缩短设计时间，科研人员正在研究将具有自学习性、并行处理能力、能够逼近任意非线性映射关系的神经网络建模方法应用到射频微波电路设计中。神经网络建模方法分为两类：一类是正向建模，有助于简化分析过程；另一类是逆向建模，就是根据已知的输出参量设计出相对应的输入参量，也就是正向建模的逆向求解。逆向建模方法的出现为神经网络的研究拓宽了视野，具有广阔的发展前景。

利用EM(ElectroMagnetic)仿真软件设计微波器件时，需要进行长时间的优化仿真来得到目标参数，非常耗时,不过可以使用精确快速的神经网络逆模型代替仿真软件求解与目标参数对应的结构参数，以简化设计[1]。在神经网络逆向建模中，直接将神经网络的输入和输出互换，经过训练就可以直接得到逆向模型[2]，它可以立即综合出与系统响应相应的元件结构参数,建模速度加快，其缺点是输入与输出之间存在多值映射关系,不能确定它的收敛性和唯一性[3]。Krishna 等人[4]和Kabir等人[5]均提出一种建立子逆模型的逆向建模方法。该方法按照一定的规则将训练数据分成若干个小组，利用每一小组的数据分别训练不同的子逆模型，然后用事先训练好的正向模型把各个子逆模型合并成一个完整的逆模型，如果合并得到的逆模型精度达到要求就结束，否则继续进行数据分组、训练直到满足逆模型的精度要求为止。Mareddy等人[6]提出一种采用共轭梯度FRCG(Fletcher Reeves Conjugate Gradient)算法的逆向神经网络建模方法，首先交换原模型中的一个输入和一个输出得到一个逆模型，依次类推建立一系列的候选逆模型；然后计算每个候选逆向模型的测量误差E，将具有最小误差的候选逆模型作为理想逆模型，采用FRCG算法优化电参数，将理想逆模型与精度不高的原模型互补得到精确模型。神经网络逆向迭代算法方面，Linden等人[7]首次提出基于梯度下降法的神经网络逆向迭代算法，即不再调整权值，而是通过更新输入参量使网络的实际输出和目标输出间的误差最小。孟少奇[8]分析了带动量项的神经网络逆向迭代算法的收敛性，该算法可以提高收敛速度，但不具有稀疏性。Xu等人[9]提出比L1/2正则项更具稀疏性的非凸罚L1/2正则项迭代算法。吕炜等人[10]证明了带L2正则化项的神经网络逆向迭代算法是确定性收敛的。黄炳家等人[11]提出的带光滑L1/2正则化项的神经网络逆向迭代算法，保证了输入向量序列在训练过程中的稳定性及稀疏性。宋雷等人[12]提出贝叶斯正则化算法能缩小BP(Back Propagation)神经网络的规模，使网络的输出更加平滑，可有效增强网络的泛化能力。李洋等人[13]指出贝叶斯正则化算法通过修正神经网络的训练性能函数来提高其推广能力。

针对以上逆向建模方法过程复杂、计算时间长、精度不够理想等缺点，本文保持训练后正向模型的权值和阈值不变，通过迭代更新输入使规则化函数为L1/2范数的贝叶斯正则化的评价函数达到最小，该逆向模型建成后，可以提高设计精度和运行速度。应用到Doherty功率放大器的设计中，验证了此逆向建模方法的高效性。此外，贝叶斯正则化算法可以提高逆向神经网络输入参量训练过程中的稳定性。

2 贝叶斯正则化神经网络逆向迭代算法

2.1 贝叶斯正则化BP神经网络

贝叶斯正则化算法是指用贝叶斯方法估计正则化参数，当比例系数大于0.5时，不仅能保证网络训练误差尽可能小，而且使网络的权值尽可能少，这实际上相当于自动缩小了网络的规模，使网络的输出更加平滑，有效增强网络的泛化性能，减少网络过拟合的可能[12 - 14]。一般神经网络的性能函数为F=E,而正则化方法是在网络误差函数E后面加入一个惩罚项Ew，那么贝叶斯正则化BP神经网络的性能函数F[13]为:

F=αEw+1-αE

(1)

其中,E为训练输出y与目标输出t之间的均方误差，α∈0,1为比例系数。在网络训练过程中，贝叶斯正则化算法能够自适应地调节α的大小，使其达到最优。

2.2 基于贝叶斯正则化的BP神经网络逆向迭代算法

神经网络逆向建模的目标就是求出与目标参数相对应的结构参数，与正向建模修正权值不同的是，逆向建模在正向模型的基础上需要调整输入参数的值，以使评价函数达到最小，此时保持权值和阈值不变，更新后获得的模型输入与目标输入之间非常接近，这样可以简化逆向建模的学习过程。输入参数的更新过程是：

(2)

其中,xn+1、xn为输入参量，η为学习速率。

正则化方法常见的规则化函数是L0，L1，L2范数。L0正则化模型是应用最早的变量选择和特征提取的正则化方法，可以产生稀疏的解，但需要求解一个NP组合优化问题来给出最优的变量选择结果。L1正则化模型较易求解，但不能总是产生最稀疏的解。L2正则化模型是最常用的方法，能产生光滑解，但不具备稀疏性，其网络剪枝能力较弱[11，15，16]。L1/2正则化模型易于求解且解的稀疏性较好，应用到贝叶斯正则化BP神经网络逆向建模中能够有效缩短网络的运行时间。当贝叶斯正则化的比例系数α较大时，可以增加网络输出的平滑性，有效提高逆向建模过程中网络的稳定性。

本文选用BP神经网络的一般结构，假设输入层有N个神经元、隐含层有P个神经元、输出层有M个神经元，如图1所示。隐含层的激活函数为logsig函数，输出层激活函数为线性purelin函数。

Figure 1 BP neural network structure图1 BP神经网络结构图

根据图1可得，隐含层神经元的输出为：

(3)

其中，zpk表示第k组数据的第p个隐含层神经元的输出，xnk是第k组数据的第n个输入值，vpn代表第n个输入与第p个隐含层神经元之间的权值，θ1p为第p个隐含层神经元的阈值，f为隐含层激活函数f=1/(1+e-x)。所以zpk对xnk的偏导为：

·zpk1-zpk

(4)

输出层神经元的输出为：

θ2m

(5)

其中,ymk为第k组数据的第m个输出层神经元的输出，wmp代表第p个隐含层神经元与第m个输出之间的权值，θ2m为第m个输出层神经元的阈值。

规则化函数为L1/2范数的神经网络逆向建模方法的评价函数为：

F=αEx+1-αED

(6)

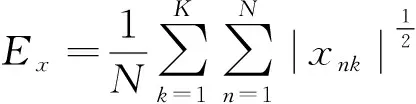
在这里，由于逆向神经网络建模方法修正的是输入值而不是权值，故将Ew替换为Ex。

那么式(6)评价函数F对第n个输入xn的偏导为：

(7)

其中，

(8)

将式(7)中的误差EDk对隐含层输出zpk求偏导得：

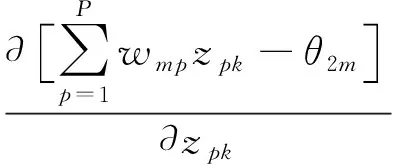
(9)

假设式(9)中的第一项由ξpk表示：

(10)

而式(9)中的第二项可以表示为:

(11)

把式(10)和式(11)代入式(9)可得：

·wmp

(12)

式(7)中误差函数EDk对输入xnk的偏导为:

(13)

将式(4)和式(12)代入式(13)可得式(14)：

·

wmp·vpn·zpk1-zpk]

(14)

由式(7)、式(8)和式(14)可得：

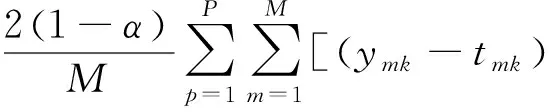
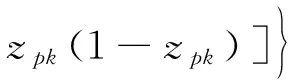
(15)

将式(15)代入式(2)中完成输入参数xn的更新过程，实现逆向建模的过程。

Figure 2 Model of Doherty power amplifier in ADS图2 Doherty功率放大器在ADS中的模型

3 逆向建模步骤

3.1 神经网络逆向建模步骤

本文将规则化函数为L1/2范数的贝叶斯正则化方法应用到BP神经网络逆向建模中，可以有效提高逆向建模过程中网络的稳定性并增强网络的泛化能力，提高模型中结构参数的精度，缩短建模的运行时间，具体实现步骤如下：

步骤1提取训练数据；

步骤2训练正向模型，获取权值和阈值并保存；

步骤3保持权值和阈值不变，在建立好的正向模型中分别输入参量，运行得到输出参量；

步骤4计算正模型输出参量与目标参量之间的评价函数F；

步骤6若达到设定的迭代次数或评价函数F满足要求，则结束,否则转到步骤3。

3.2 Doherty功率放大器逆向神经网络建模过程

将本文提出的逆向建模方法应用到Doherty功率放大器中，图2和图3是在ADS中搭建的Doherty功率放大器模型，图4为该Doherty功率放大器的实物图。

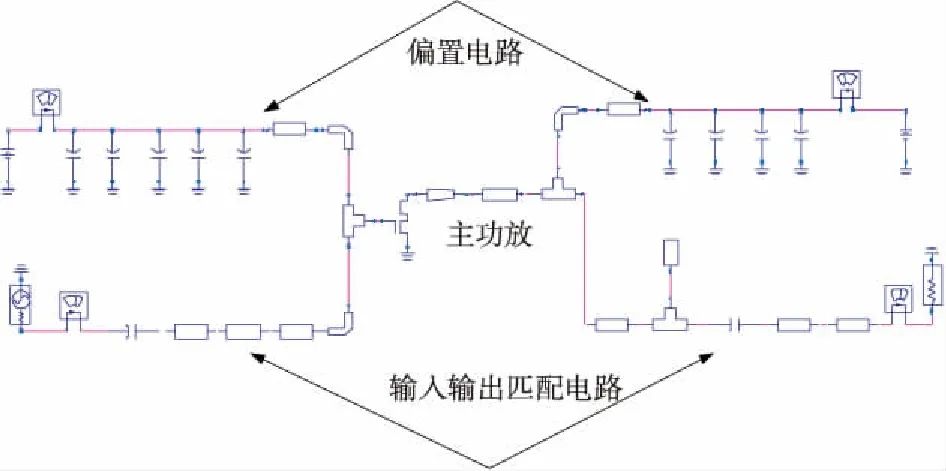
Figure 3 Carrier amplifier model of Doherty power amplifier in ADS图3 Doherty功率放大器在ADS中的载波放大器模型

Figure 4 Physical map of Doherty power amplifier图4 Doherty功率放大器的实物图

如图2所示是Doherty功率放大器的模型，它由一个主功放即载波放大器和一个辅功放即峰值放大器组成，主辅功放通过λ/4微带线进行连接。载波放大器输出端的λ/4传输线起着阻抗变换的作用，而峰值放大器输入端λ/4传输线则起着相位补偿的作用，用以平衡载波放大器和峰值放大器的相位。在低功率的时候，载波功放导通，峰值功放关闭，随着输入功率的提高，载波功放开始出现压缩，这时峰值功放开始工作，补偿载波功放的压缩。这两个功率放大器的输出功率经过λ/4阻抗变换网络合成后，得到一个合成功率的输出，这样可以提高功率放大器的效率，尤其是功率回退时的效率。当主辅功放电路谐振在中心频率处时，S11应达到最大，S21应几乎接近于零点。但是，在实际设计中，微带线两端的阻抗并不相同，因此频率会产生偏移。设计者使用ADS软件调节输出功率和频率f得到需要的效率、S11和S21是非常耗时的。如图3所示是Doherty功率放大器的载波放大器模型，其输出功率与效率、输出匹配端频率f与回波损耗S11和插入损耗S21之间的关系如图5a～图5c所示。

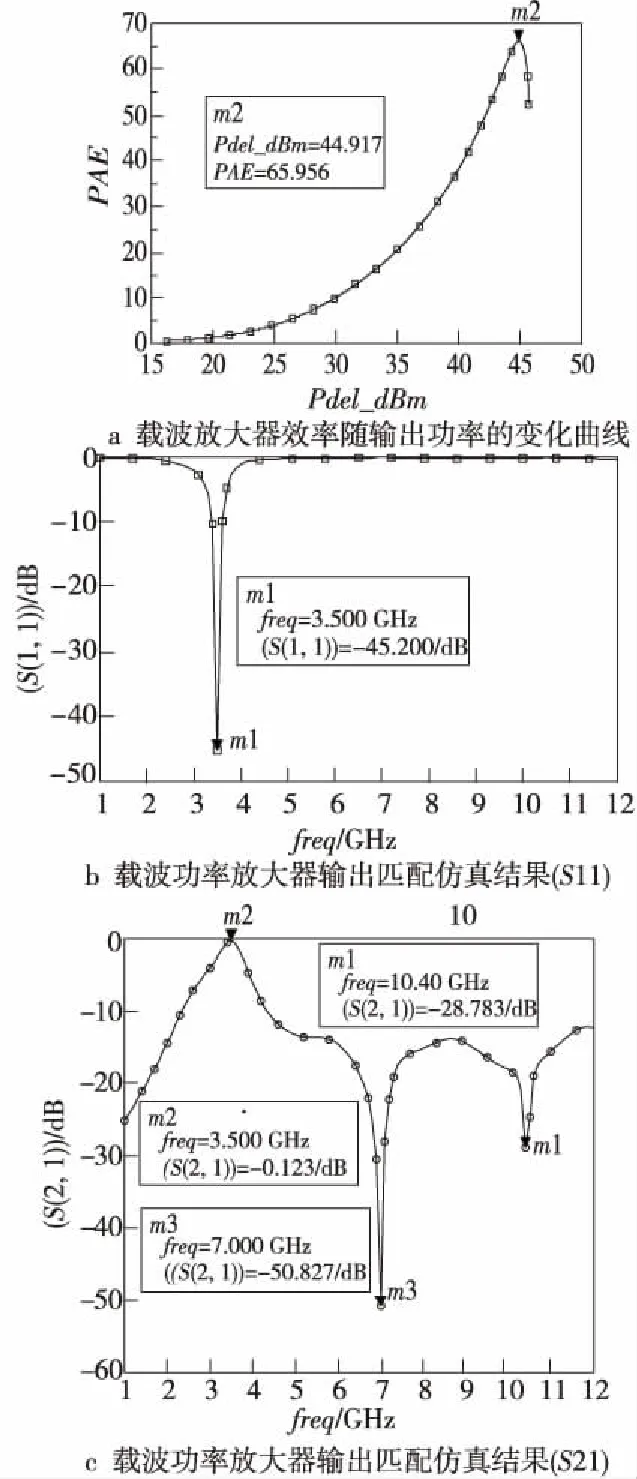
Figure 5 Relationship between output power and efficiency, output matching f and S11、f and S21图5 输出功率与效率、输出匹配端f与S11和f与S21的对应关系

图5a为载波放大器效率随输出功率的变化曲线图，图5b、图5c分别为载波功率放大器输出匹配仿真结果图，其中S11,S21的单位是dB。由图5a可知，当输出功率为44.92 dBm时，效率最大可达65.96%。图5b和图5c显示在频率3.5 GHz时，S11为-45.20 dB，S21为-0.12 dB，达到了良好的匹配效果。从该图可以看出，相同的效率对应多个输出功率值，相同的S11和S21也分别对应多个f值。为解决以上设计耗时和各参数呈非线性映射关系的问题，可以利用本文提出的逆向建模方法求解与所需效率、S11和S21分别对应的最佳输出功率值和f值，以简化设计步骤，具体建模过程如图6所示。

Figure 6 Flow chart of the reverse modeling method图6 逆向建模方法流程图

4 实验验证及仿真分析

为了验证所提出的逆向建模方法具有高精度和运行时间更少的特性，以Doherty功率放大器中载波放大器的输出匹配端为例，将本文逆向建模方法与ADS仿真方法、直接逆向建模方法的结果作比较。

直接逆向模型就是将输入输出参量互换，建成网络后，只要输入目标参量，就可以获得相应的结构参量。在载波功率放大器中提取出输出功率与效率、输出匹配端S11与f和输出匹配端S21与f的数据，每个参数均提取3 688组，从中分别选取1 000组为训练数据，另分别取150组数据为测试数据。规则化函数为L1/2范数的贝叶斯正则化神经网络逆向建模方法使用和直接逆向模型相同的训练数据和测试数据，按照第3.2节的实现过程训练模型。在Matlab 2013b中实现对网络的训练和测试，直接逆向建模方法和本文逆向建模方法均采用结构为1-30-1的BP神经网络，学习速率η取0.01，误差限设定为1e-6，迭代500次。另外，本文逆向建模方法评价函数中的比例系数取0.65。针对150组测试数据，利用这两种方法求得的与效率相对应的输出功率值和ADS软件中的输出功率值的拟合情况如图7所示，与S11相对应的频率f值和ADS软件中的f值的拟合情况如图8所示，与S21相对应的频率f值和ADS软件中的f值的拟合情况如图9所示。

Figure 7 Comparison of output power图7 输出功率的对比图

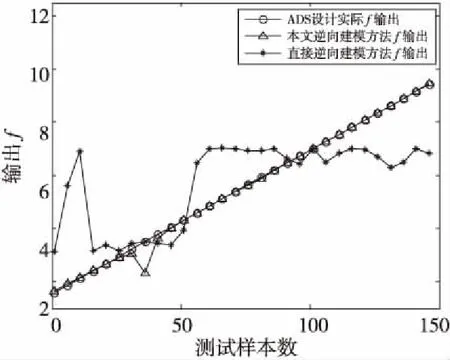
Figure 8 Comparison of frequency valuescorresponding to S11图8 与S11相对应的频率f值的对比图

Figure 9 Comparison of frequency valuescorresponding to S21图9 与S21相对应的频率f值的对比图

从图7～图9可以知道，直接逆向建模方法求得的值与ADS中的值基本上都不拟合。由图5可以知道，输出功率与效率、S11与f和S21与f的对应关系是一对多的，直接逆向建模方法无法给出最优值，因此不能用来描述载波功率放大器的特性。而本文逆向建模方法求得的值与ADS中的值拟合效果比直接逆向建模方法要好很多，在精度方面，该方法能够满足实际的设计需求。

在这里，分别利用直接逆向建模方法和本文逆向建模方法，在已知效率的情况下综合出输出功率、已知S11、S21时分别综合出相对应的频率f，比较这两种逆向建模方法的建模时间和均方误差，如表1所示。本文逆向建模方法求得与S11相对的f、与S21相对的f和输出功率的运行时间分别比直接逆向建模方法减少了9.30%、9.00%和8.83%，均方误差分别减少了99.40%、99.23%和99.34%。由表1可知，规则化函数为L1/2范数的贝叶斯正则化神经网络逆向建模方法不仅可以提高网络的稳定性和泛化能力，而且可以缩短网络的运行时间。

Table 1 Performance comparison ofthe two modeling methods

5 结束语

本文提出了一种基于贝叶斯正则化的神经网络逆向建模方法，该方法采用的规则化函数为L1/2范数，能够使网络稀疏化，进而缩短网络模型的运行时间。当贝叶斯正则化方法的比例系数α较大时，可以平滑输出，提高逆向建模过程中网络的稳定性和网络的泛化能力。将该方法应用到Doherty功率放大器中，并在Matlab中与直接逆向建模方法的仿真结果作比较，验证了该方法的高精度和高速度，表明该方法适用于射频微波器件的设计。