测试代价受限下数据的属性和粒度选择方法
2018-08-23廖淑娇朱清新
廖淑娇,朱清新,梁 锐
(1.电子科技大学信息与软件工程学院,四川 成都 610054;2.闽南师范大学数学与统计学院,福建 漳州 363000)
1 引言
代价敏感学习是数据挖掘领域的一个重要研究方向[1]。迄今为止,不少学者已对其理论和应用进行了较为深入的研究[2 - 11]。一般来说,相比主要追求高分类精度的非代价敏感学习方法,代价敏感学习技术由于考虑了现实的代价因素,因此更有实际意义。测试代价和误分类代价是最常考虑的两种代价[12]。其中,测试代价(也称获取代价)是指人们为了获得样本(也称对象)某个数据项的值而对该样本进行测试所付出的代价,例如医疗检查中抽血检验所花费的金钱就是该检查项目的测试代价。当一个样本具有多个数据项,即具有多个属性时,所检测的所有属性的测试代价之和称为总测试代价。而误分类代价则是由错误分类所导致的代价,不同的分类错误经常造成不同大小的代价。例如,在银行发放贷款的风险评估中,将低信用等级的客户误评为高信用等级一般比将高信用等级的客户误评为低信用等级具有更高的误分类代价。
在数据值的获取/测试过程中,由于观测者的水平不同或者观测工具的条件有限,观测误差广泛存在。对于同一个量来说,不同人或不同工具得到的观测误差一般服从正态分布。数据的误差范围越大,它的粒度就越粗,反之则越细。以往的代价敏感学习经常假设测试代价和误分类代价是固定不变的,事实上这两类代价往往都是可变的。一方面,测试代价与数据粒度有密切的关系,要得到越精确的数据值,即希望数据粒度越细时,需要的测试代价往往越高。另一方面,误分类代价又常受总测试代价大小的影响,对于同样的错误分类,当已付出的总测试代价越高时,误分类代价也常常跟着增多。此外,现实中还存在测试代价受限,即总测试代价受到一定约束的情况。
在当今的大数据时代,一个数据集经常含有很多个属性,这导致了数据分类处理的复杂性。作为一种常用的数据预处理技术,属性选择着力于去除数据集中冗余或不相关的属性,从而提高数据后续处理的效率。此外,粒度也是数据处理中经常考虑的一个问题。虽然已经有学者分别研究了测试代价受限情况下的属性选择[13]和不受限情况下的粒化问题[14],但并没有考虑到测试代价受限下属性和粒度的同步选择。基于这种情况,本文着眼于研究在测试代价受限的情形下,基于误差和可变代价的属性和粒度选择方法,其中粒度选择指的是选择数据合适的误差范围。
本文以最小化数据集在测试与分类过程中所付出的平均总代价(总代价的平均值)为目标,提出了一种测试代价受限的属性和粒度同步选择的方法,其中数据的粒度用观测误差的置信水平来衡量。误差置信水平越高,数据粒度越粗。本文首先建立了包含误差置信水平、误差区间、邻域模型和可变的代价函数等内容的理论模型;接着提出了一个高效的属性和粒度选择的算法,其中运用了三个剪枝技术以提高算法的效率;最后,在多个UCI数据集的实验结果表明,所提算法能针对不同大小的总测试代价约束进行有效的属性和粒度选择,并且揭示了算法所得的最优属性子集和最优数据粒度随着总测试代价上限的大小变化的规律。
2 理论模型
本节建立理论模型,从而为下一节的算法设计提供理论依据。首先根据置信水平和置信区间的关系给出了属性的误差边界和误差区间的计算方法;接着建立了基于误差置信水平的邻域模型,然后结合现实情况分别设计了可变的测试代价函数和误分类代价函数;最后给出了数据集中对象测试与分类的平均总代价的计算方法。
2.1 误差置信水平与误差区间

根据数据观测误差的特点,假设误差服从均值为0的正态分布,而数据粒度的大小用误差置信水平来衡量。如前文所述,一个数据集经常含有多个属性,令σa表示数据集中所有对象关于属性a的观测误差所服从的正态分布的标准差,e(a,p)表示这些对象关于属性a和置信水平p的观测值的误差边界,则有:
e(a,p)=σa·zp
(1)



(2)
其中,λ>0为调节系数。结合式(1)和式(2),可以计算得到数据集中对象关于属性a和置信水平p的误差边界e(a,p),从而得到误差区间[-e(a,p),+e(a,p)]。显然,误差边界和误差区间随着置信水平的增大而增大,这时数据精度下降,数据粒度变粗。
2.2 基于误差置信水平的邻域模型
决策系统和邻域是数据挖掘中的常用概念。本节分别给出基于误差置信水平的决策系统和邻域的定义如下。
定义1称六元组S=(U,C,D,V,I,p)为基于误差置信水平的决策系统ECLDS(Error-Confidence-Level-based Decision System),其中,U为对象的集合,称为论域;C为条件属性的集合;D为决策属性的集合;V={Va|a∈C∪D},Va为属性a的值域;I={Ia|a∈C∪D},Ia:U→Va为信息函数;p∈(0,0.997]为误差置信水平。
定义2设S=(U,C,D,V,I,p)为一个ECLDS,则对于任意的x∈U,a∈C,对象x的基于属性a和误差置信水平p的邻域为:
N(a,p)(x)={y∈U‖a(y)-a(x)|≤2e(a,p)}
(3)
这里分析选择2e(a,p)而不是e(a,p)作为邻域中对象的最大距离的原因。在误差环境中a(x)是对象x关于属性a的观测值,设x关于属性a的真实值为a′(x),则有a′(x)-e(a,p)≤a(x)≤a′(x)+e(a,p),即a′(x)-e(a,p)和a′(x)+e(a,p)可能为同一个对象的观测值,这时|(a′(x)+e(a,p))-(a′(x)-e(a,p))|=2e(a,p),所以对象x的邻域N(a,p)(x)必须包含所有观测值跟a(x)的距离不超过2e(a,p)的对象。
由式(3)可知,对于任意的x∈U,B⊆C,x基于属性子集B和误差置信水平p的邻域为:
N(B,p)(x)=∩a∈BN(a,p)(x)
(4)
即对象关于属性子集的邻域是关于单个属性的邻域的交集。由以上邻域的定义及分析可知,一个对象的邻域中的所有元素跟这个对象本身是不可区分的。
由式(3)和式(4),可得到邻域N(B,p)(x)分别关于属性子集B和误差置信水平p的单调性,如以下两个定理所示。
定理1(关于属性子集的单调性) 设S=(U,C,D,V,I,p)为一个ECLDS,B1⊆B2⊆C,则对于任意的x∈U,有:
N(B1,p)(x)⊇N(B2,p)(x)
定理2(关于置信水平的单调性) 设S=(U,C,D,V,I,p)为一个ECLDS,B⊆C,p1 N(B,p1)(x)⊆N(B,p2)(x) 由以上两个定理可知,同一个对象的邻域随着属性子集的增大而缩小,随着误差置信水平的增大而扩大。 本小节根据现实中测试代价和误分类代价变化的特点来设计这两类代价函数。 首先讨论属性的测试代价。如前面所述,一个属性的测试代价一般随着数据粒度的变细而增加,而数据粒度用误差置信水平来衡量;当置信水平增加时,数据精度下降,数据粒度变粗,所以测试代价是误差置信水平的单调递减函数。用tc(a,p)表示属性a基于置信水平p的测试代价,设: (5) tc(B,p)=∑a∈Btc(a,p) (6) 即总测试代价是属性集中每个属性测试代价的和。 接着讨论对象的误分类代价。如前所述,误分类代价经常随着总测试代价的增加而增大。令二元组(h,k)表示把属于第h类的对象误分到第k类,简称为一个误分类别对,mc(h,k)(B,p)表示误分类别对(h,k)在属性子集为B和置信水平为p的条件下的误分类代价。显然,当h=k即正确分类时,mc(h,k)(B,p)=0。当h≠k时,令: tc(B,p)∈[TTCj-1,TTCj],j=1,2,…,n (7) 值得注意的是,由于篇幅所限,本文仅给出分段常值函数形式的测试代价和误分类代价函数,研究者也可根据实际情况设计其他类型的代价函数。 如前所述,本文以最小化论域中对象测试与分类的平均总代价为目标,寻找最优的属性子集和数据粒度。平均总代价由两部分组成:论域中对象的平均测试代价和平均误分类代价。为了简便起见,本文假设论域中每个对象的测试属性集和误差置信水平都分别一样,显然这些对象基于属性子集B和置信水平p的平均测试代价等于每个对象分别的总测试代价,即为tc(B,p)。 接下来分析平均误分类代价的计算方法。第一步也是关键的步骤是,对于论域中的每个对象,根据其邻域的情况对其进行分类,得到该对象的误分类代价,分类依据是一个邻域中对象的不可区分性以及最小化邻域中对象的总误分类代价这两个原则。具体地,用mc(x,B,p)表示对象x基于属性子集B和误差置信水平p的误分类代价,则根据邻域N(B,p)(x)的情况有两种可能:(1)当N(B,p)(x)中所有对象的决策属性值一样时,则可以将这些对象包括x分到正确的类别,这时mc(x,B,p)=0;(2)当N(B,p)(x)中对象的决策属性值不完全一样时,则根据使N(B,p)(x)中所有对象的误分类代价总和最小的原则将x分到相应的类别,这时即可得到mc(x,B,p)。接着,计算论域U中对象的总误分类代价和平均误分类代价,分别为: TMC(U,B,p)=∑x∈Umc(x,B,p) (8) 和 AMC(U,B,p)=TMC(U,B,p)/|U| (9) 综上,可得平均总代价为: ATC(U,B,p)=tc(B,p)+AMC(U,B,p) (10) 本节设计了测试代价受限情形下数据的属性和粒度同步选择的算法。该算法由算法1和算法2组成。 算法1测试代价受限的属性和粒度同步选择算法 输入:决策系统S=(U,C,D,V,I,p), 总测试代价的上限值w,最小置信水平p0,置信水平的递增步长r,每个属性的测试代价函数,每个误分类别对相应的误分类代价函数。 输出:全局的最小平均总代价gmtc和最优属性子集R*以及最优误差置信水平p*。/*它们都是全局变量*/ (1)gmtc=+∞;//gmtc表示全局最小平均总代价 (2) for (p=p0;p≤0.997;p=p+r) do (3) 得到置信水平p下每个属性a的测试代价tc(a,p); (4)cmtc=+∞;/*cmtc表示当前置信水平下最小平均总代价*/ (5)B=∅;//当前测试属性集 (6)cttc=0;//当前的总测试代价 (7)backtracking(B,cttc,1);/*调用算法2,得到cmtc和R*/ (8) if (cmtc (9)gmtc=cmtc;//更新全局最小平均总代价 (10)R*=R;//更新全局最优属性子集 (11)p*=p;//更新最优置信水平 (12) end if (13) end for 算法2回溯算法backtracking(B,cttc,l) 输入:当前的测试属性集B和总测试代价cttc,以及当前搜索路径下属性指标的起始值l。 输出:当前置信水平下的最小平均总代价cmtc和最优属性子集R。/*它们都是全局变量*/ (1) for (i=l;i≤|C|;i++) do (2) if (tc(ai,p)≥cmtc||tc(ai,p)>w) then (3) continue;//剪枝,摒弃测试代价过高的属性 (4) end if (5)B=R∪{ai}; (6)tc(B,p)=cttc+tc(ai,p); (7) if (tc(B,p)≥cmtc||tc(B,p)>w) then (8) continue;/*剪枝,摒弃总测试代价过高的属性子集*/ (9) end if (10) 得到每个误分类别对(h,k)相应的误分类代价mc(h,k)(B,p); (11) 计算每个对象的邻域和误分类代价; (12) 计算平均误分类代价AMC(U,B,p); (13)ATC(U,B,p)=tc(B,p)+AMC(U,B,p); (14) if (ATC(U,B,p) (15)cmtc=ATC(U,B,p);/*更新当前最小平均总代价*/ (16)cttc=tc(B,p);//更新当前总测试代价 (17)R=B;//更新当前最优属性子集 (18) end if (19)backtracking(B,cttc,i+1);//再下一层搜索 (20) end for 算法1中,误差置信水平由最小值p0(p0>0,可由用户根据具体情况给定)逐步递增到最大值0.997。对于每个置信水平,其相应的最小平均总代价和最优属性子集由算法1调用算法2得到,再将该平均总代价与现有的全局最小平均总代价进行比较,从而得到全局最优的属性子集和误差置信水平。特别地,当总测试代价不受限时,可设算法1中的输入量w=+∞,所以测试代价不受限可看成有受限的特殊情形。 算法2是一个回溯算法,它使用了三个剪枝技术以提高效率。 首先,如第1行所示,回溯算法的搜索路径中属性指标的起始值l不是都从1开始,而是随着算法的进行在递增的,这样减少了搜索工作量;其次,如第2行~第4行所示,当单个属性的测试代价过高时,则进行剪枝;最后,如第7行~第9行所示,当属性子集的总测试代价过高时,也进行剪枝。后面两个剪枝主要是基于平均误分类代价不小于0的特点而提出的。这三个剪枝技术能较大程度地提高算法的效率。 为了验证所提出的属性和粒度选择算法的性能,本文使用了7个常用的UCI数据集进行实验。如表1所示,这些数据集分别涉及到医疗、金融、物理和图形学等领域,因此具有较强的代表性和现实意义。在实验中,令误差置信水平的最小值p0和递增步长r都为0.1,式(2)中正态分布的标准差的调节系数λ=0.05;令每个属性的测试代价为其值介于10和100之间的分段常值函数,它们随着误差置信水平的增高而递减;令每个误分类别对的代价为其值介于500和10 000之间的分段常值函数,它们随着总测试代价的增大而递增。 Table 1 Dataset information 通过实验发现,运用算法可以得到不同大小的总测试代价上限下最优的属性子集和数据粒度;算法的运行时间较短,并且总测试代价的上限越低,算法的运行时间越短,这是因为剪枝技术在起作用。此外,不同数据集在属性和粒度的选择结果随总测试代价上限的大小变化方面服从类似的规律。表2~表4和图1给出了每个数据集的一组代表性实验结果,其中的最大总测试代价指的是测试代价不受限情况下最优的属性和粒度选择结果相应的总测试代价值。具体地,表2~表4分别列出了Diab、Liver和Wpbc三个数据集的最优置信水平和最优属性子集以及相应的三种代价值;而为了直观起见,对于其他四个数据集,则画出了平均测试代价和平均总代价的变化趋势图,如图1所示,显然每个子图中同一横坐标对应的平均总代价和平均测试代价的差值就是平均误分类代价(事实上,如2.4节所述,数据集中对象的平均测试代价等于单个对象的总测试代价)。 Table 2 Representative experimental results of Diab dataset,where the maximum total test cost is 128.746 Table 3 Representative experimental results of Liver dataset,where the maximum total test cost is 154.034 4 Table 4 Representative experimental results of Wpbc dataset,where the maximum total test cost is 77.518 1 Figure 1 Cost comparison under different sizes of constraint图1 不同大小的约束下的代价对比图 从这些图表中可以发现,随着测试代价受限程度的增强,即随着总测试代价的上限占最大总测试代价比例的减少,所得最优误差置信水平可能不变也可能改变,但当所得最优属性子集不变时,最优置信水平一般会增加(如表3中第4~6行),表示放宽对相同属性的数据精度要求;最优属性子集的维度呈现减少的趋势,具体地,维度可能逐渐减少(如表3和表4所示),也可能先增加后减少(如表2所示);平均测试代价递减,平均误分类代价递增,平均总代价除极个别外也递增。而当总测试代价的上限相当低时,所得属性子集为空集,如表2~表4的最后一行所示,以及图1中四个子图的横坐标有的只到20%,有的只到30%,即当上限值占最大总测试代价的比例为10% 或20% 时,没办法得到非空的属性子集。 从以上实验结果发现的规律和现实情况是吻合的。以医疗为例,当看病的人能承担的费用越有限时,他/她不得不更多地减少必须检查的项目,或降低对这些项目的精度要求,或替换成测试代价较低但分类能力较差的项目(如表2中第4~6行所示),从而导致误分类(误诊)可能性较大程度地增大,所以平均误分类代价增高,平均总代价一般也增高。而当病人能承担的费用实在低时,即使他/她再降低对检查结果精度的要求,即误差置信水平再高,也没有合适的检查项目满足要求。 考虑到数据值获取过程中经常存在误差,并且属性的测试代价和样本的误分类代价经常随着误差范围的大小而变化,还有样本的总测试代价大小有可能受到约束等因素,本文提出了测试代价受限情况下的一种属性和粒度同步选择的方法,充分讨论了相关的理论知识,并设计了一个较为高效的算法。实验结果验证了所设计算法的有效性,并分析了属性和粒度选择结果随总测试代价上限的大小变化的规律。本文为代价敏感学习的实际应用提供了理论和技术支持。接下来拟进一步改进算法以高效求解大型数据集的相关问题。2.3 可变的代价函数



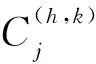
2.4 平均总代价的计算方法
3 算法设计
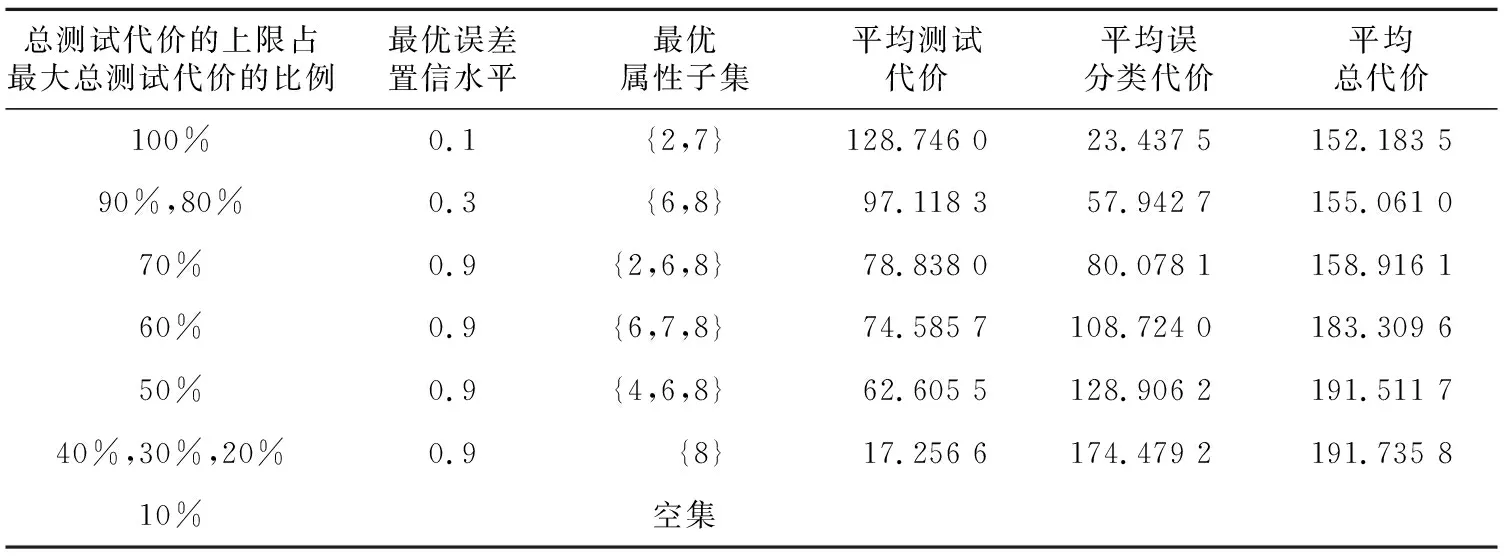
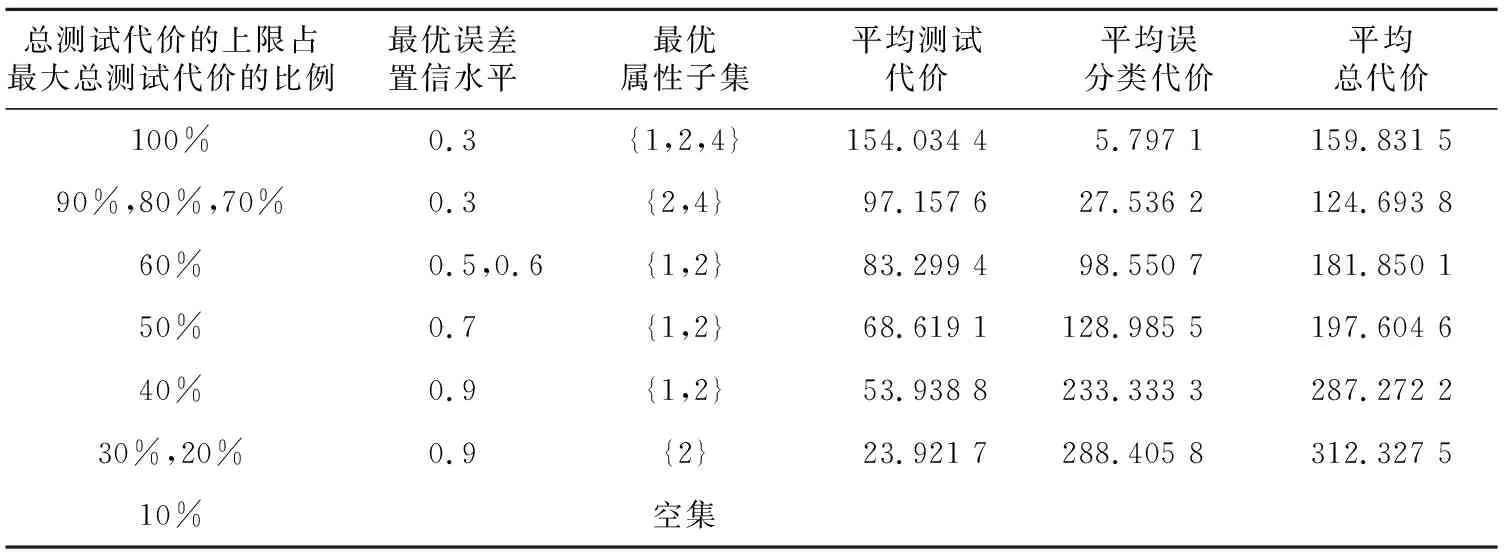
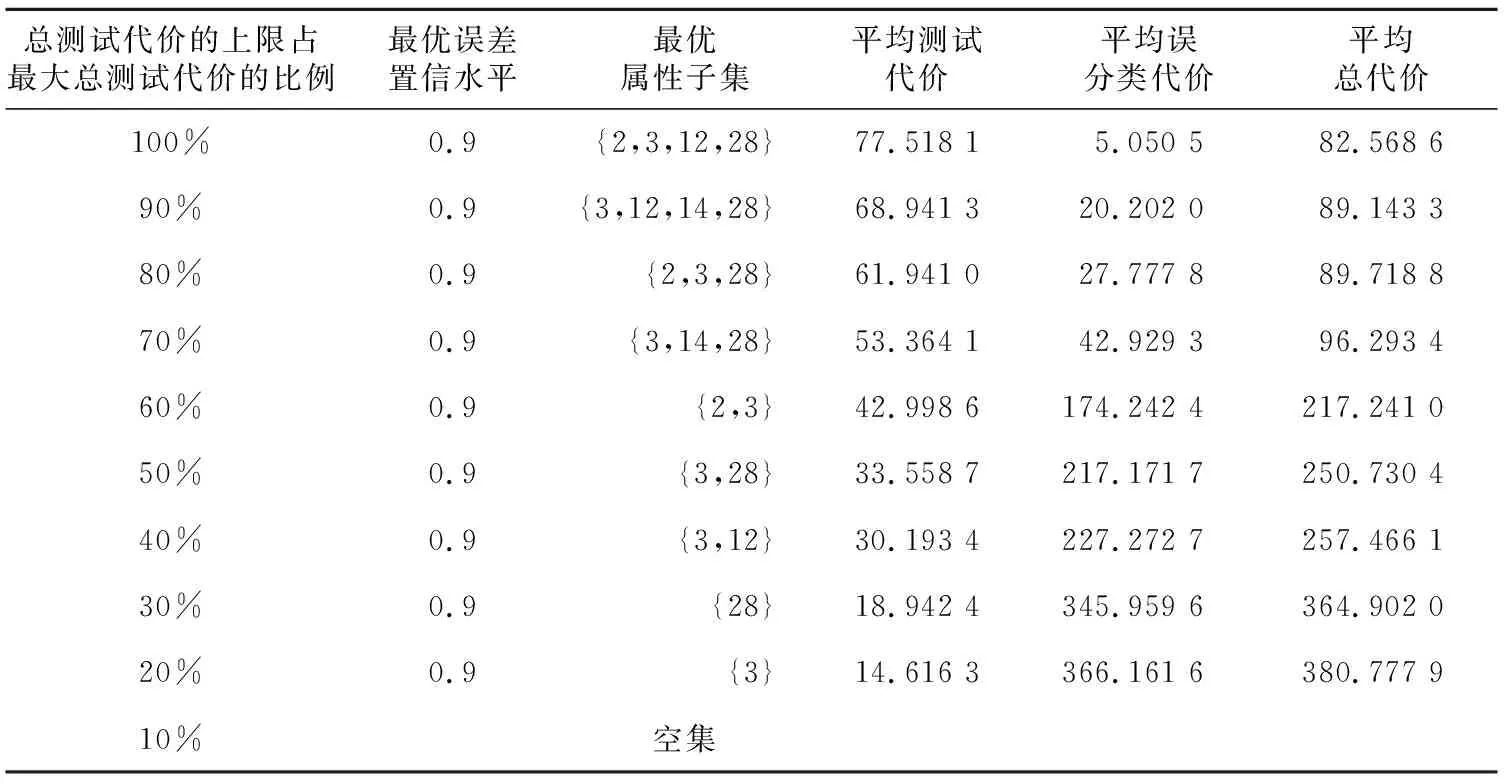
4 实验与分析


5 结束语
