移动感知环境下基于CSA-SSVR的交通状态预测方法

夏卓群,罗君鹏,胡珍珍

(1.长沙理工大学综合交通运输大数据智能处理湖南省重点实验室，湖南 长沙 410114;2.长沙理工大学计算机与通信工程学院，湖南 长沙 410114;3.国防科技大学计算机学院，湖南 长沙 410073)

1 引言

随着城市化水平的不断提高，智能交通系统ITS(Intelligent Traffic System)得到了长足发展[1]。移动群智感知技术利用用户手中的移动设备作为感知单元采集数据[2,3]，通过已有的基础网络设施传输数据到数据中心，由于移动设备的普及，可以较为轻易地获得较大范围内的细粒度感知信息，相比传统信息采集系统获取的感知信息精度更高[4]，同时还具有部署、维护成本低的优势[5]，在智能交通系统中起到了越来越重要的作用。交通状态预测是智能交通领域的一项重要研究内容，它可以帮助交通管理部门更加合理地进行交通管理和控制，也可以向驾驶员提供出行时间的实时估计、出行路线的规划。传统的基于实时数据的交通控制与诱导对交通状态缺乏预见性，且有明显的滞后性，交通状态是有可能在短时间内发生大幅度变化的，如道路在下班高峰时期可能会突然拥堵，而这段时间过后又会恢复正常，因此预测的信息对于交通管控部门与驾驶员来说有时候比实时信息更加有用[6,7]。

移动群智感知网络通过用户手中的移动设备，可以获取用户行车过程中的位置和速度信息，将这些信息分类聚合，可以得到一定范围内每个路段带有时间戳的道路车速信息[8]。由于这些信息要由用户设备主动上传，移动群智感知目前存在参与用户不足、采集数据质量不够高等问题[9,10]，因此对于这些缺失的数据，需要进行数据补齐。利用补齐后的信息，可以对道路未来的车速进行预测，同时，道路车程速度可以用来判断道路拥堵情况，从而实现对交通状态的预测。

近年来，国内外学者们提出了许多车速的预测方法，较早期的有Danech-Pajouh和Aron[11]提出的利用自回归积分移动平均模型ARIMA(Autoregressive Integrated Moving Average Model)进行预测，该模型专注于过去的平均值序列，对于快速变化的交通情况不敏感；随后，学者们又将目光转向了人工神经网络ANN(Artifical Neural Networks)方法，该方法预测的结果更加准确，但是在训练过程中容易陷入局部最优解；支持向量机SVM(Support Vector Machine)方法常被应用于解决各种预测问题[12]，比起人工神经网络，该方法不容易陷入局部最优解。而在支持向量机方法中，最重要的是模型中几个主要参数的确定，常用的网格式搜索算法、遗传算法在这方面均有不错的表现[13]，而近年有学者提出的布谷鸟搜索算法CSA(Cuckoo Search Algorithm)[14]在支持向量回归SVR(Support Vector Regression)算法的参数确定方面表现出了收敛更快、有效避免陷入局部最优解的特点[15]。Williams等[16]发现道路路况根据时段具有一定的规律，首次将周期性引入车速预测算法中，提出了周期性ARIMA模型，在SVR预测中同样可以引入周期性方法，以提高对车速预测的准确性[17]。SVR模型常被用于解决非线性回归估计问题，在各个领域的数值预测中有着广泛应用。本文针对城市道路车流量所具有的周期性规律，将周期性引入SVR模型，并采用布谷鸟算法确定其参数，来完成对车速较为准确的预测。因此，本文基于CSA-SSVR(Cuckoo Search Algorithm—Seasonal Support Vector Regression)数据预测路段车速，实现对道路交通状态的预测，可以为交通控制与诱导提供较准确的预测信息。

本文在第2节中详细介绍了CSA-SSVR预测方法；第3节提出了移动感知环境下基于CSA-SSVR的交通状态预测模型；第4节为实验；第5节为结束语。

2 基于CSA-SSVR模型的车速预测方法

2.1 SVR模型原理

近年来支持向量回归SVR算法被广泛应用于解决非线性回归和时间序列问题。它的基本思想是针对有限样本，通过非线性变换将实际问题转换到高维空间中，在其中构造线性决策函数实现线性回归。

对于输入序列X=(x1,x2,x3,…,xi)，支持向量回归函数如公式(1)所示：

f(x)=wTφ(x)+b

(1)

由于数据可能有噪音，引入松弛变量ξi≥0，于是问题转化为求解

ξi,s.t.,yi(wTxi+b)≥

1-ξi,ξi≥0,i=1,…,n

在非线性问题中，为了避免因为映射到的线性空间维度过高导致难以计算，引入核函数K(x,z)=〈φ(x)·φ(z)〉来解决这个问题。支持向量机首先在低维空间中计算数据，然后利用核函数将数据空间映射到高维空间中，并在其中构建超平面，从而完成数据分类。最常用的核函数是高斯核函数K(x1,x2)=exp(-‖x1-x2‖2/(2σ2))，令g=-(1/(2δ2))，称为控制半径。

2.2 周期性SVR算法

根据预测速度y=f(x)，使用Lagrange 乘子法优化SVR函数，可建立预测算法如公式(2)所示：

βi)K(xi,x)+b

(2)

…+peak(m-1)l+j)

βi)K(xi,xN+k)+b)×SIk

(3)

该方法的预测精度主要受到惩罚因子C和控制半径g的影响，可以采用布谷鸟搜索算法确定这两个参数。

2.3 使用布谷鸟搜索算法进行参数寻优

布谷鸟搜索算法通过模拟布谷鸟的寄生育雏行为，结合Levy飞行以求解最优化问题。在SVR的参数确定问题中，该算法相比常用的网格式搜索算法、遗传算法，能更有效地避免陷入局部最优解。

布谷鸟算法假定：

(1)一只鸟一次产一个卵，然后随机选择一个寄生鸟巢来孵化它。

(2)仅保留鸟巢中最好的卵到下一代。

(3)可选寄生鸟巢固定为n个，宿主发现寄生卵的概率为Pa∈[0,1]。若宿主发现寄生卵，则该卵被抛弃。

寄生鸟巢中原有若干卵，分别代表一种解决方案，寄生卵代表一种潜在较好的解决方案，用于代替原有较差的方案。布谷鸟算法表述如公式(4)所示：

α⊕L

(4)

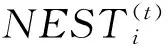
算法流程如图1所示。其中，g(NEST)需要确定C和g两个参数，设允许接受的最大值为g(Tol)，最大迭代次数为T，第i代表述为NESTi=(xC,xg)。输出条件分两步判断：若g(NESTi)≤g(Tol)，则输出当前最优解；若迭代次数t=T，则输出当前g(NESTi)。

Figure 1 Process of the cuckoo search algorithm图1 布谷鸟搜索算法流程

2.4 车速预测流程

首先，采集某一路段的交通数据，确定车速时间序列为自变量，需要预测的车速为因变量，代入周期性SVR(SSVR)中；然后采用布谷鸟搜索算法CSA训练SSVR中的C和g两个参数，将确定的参数代入SSVR中，即可使用该方法对该路段车速进行预测，称为基于布谷鸟搜索算法的周期性SVR方法(CSA-SSVR)。

3 移动感知环境下基于CSA-SSVR的交通状态预测模型

3.1 移动群智感知数据处理

移动群智感知利用用户所拥有的终端设备进行感知，虽然具有建设维护成本低的优点，同时也带来了数据采集不完整、容易丢失数据的缺点，本文采用插值法补齐缺失数据。具体方法如下：

根据定位信息，将所有经过同一路段的车辆平均速度数据按时间戳进行整理，令标准时间周期为tv，第n个标准时间周期记为tv n，统计tv n内所有采集到的车速信息数据的平均值，记为Vn，若tvi内无上传数据，则采用插值法补齐数据，如公式(5)所示：

Vni=Vni+k+1-Vni+k+Vni-1

(5)

其中,k为正整数，Vni+k为获取到的最接近Vni的一个速度数据，补齐后的数据可用于后续处理。

3.2 车速预测与交通状态判别

根据《城市交通管理评价指标体系》，城市主干道的交通状态可以用机动车的平均行驶速度V判别。

Table 1 Correlation between traffic state and speed

由表1的标准，在预测车速的基础上可以导出预测的交通状态。

3.3 建立基于CSA-SSVR的交通状态预测方法

步骤1采集数据；

步骤2按照路段与时间分类整理数据；

步骤3对于单个路段，按照时间戳排列数据，判断并补齐缺失数据；

步骤4使用基于布谷鸟搜索算法的周期性SVR方法预测未来车速；

步骤5根据预测车速导出预测的道路交通状态，并提供给用户。

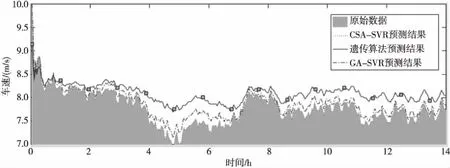
Figure 2 Forecasting result comparison between the CSA-SSVR and other algorithms in experiment 1图2 车速预测模型对比分析结果图

4 性能评估与分析

为了验证本文预测模型的有效性以及与其它方法相比的优势，本文分别做了车速预测方法对比分析、交通状态预测分析。

4.1 车速预测方法对比分析

采用Vissim模拟城市车流情况，仿真范围内共有五个十字路口，四个三岔路口，输入车流中主要有小型私家车、货车、公交车、非机动车以及行人等五种类型，驾驶行为习惯选择城市，道路输入流量按照工作日上下班时间存在高峰期的特点设置波动值；然后从中提取每辆车在经过其中某个特定路段的平均车速数据，基于时间序列进行整理；然后使用Matlab平台上的Libsvm工具进行仿真实验。使用标准均方根误差和相关系数来定量地比较寻优结果的好坏，标准均方根误差如公式(6)所示：

(6)

相关系数如公式(7)所示:

(7)

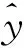
我们将采集到的时间序列数据分为两组，一组为训练数据，一组为验证数据。分别采用BP神经网络、基于遗传算法的SVR预测方法(GA-SVR)、基于布谷鸟搜索算法的周期性SVR预测方法(CSA-SSVR)三种方法对该路段的车速进行预测，对比它们的预测结果与原始数据。其中BP神经网络进行200次训练，GA-SVR中遗传算法训练参数的最大进化代数为200，CSA-SSVR中布谷鸟算法训练参数的最大代数为200。各方法的预测结果均方根误差和相关系数见表2,预测结果对比见图2。

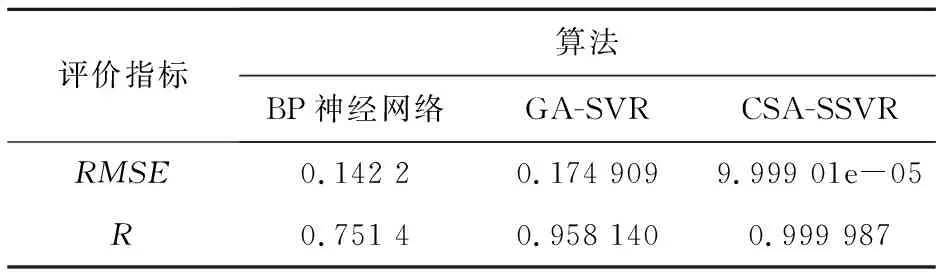
Table 2 Forecasting result comparison between theCSA-SSVR and other algorithms in experiment 1

由表2可以看出，车速预测问题中，CSA-SSVR预测模型的标准均方根误差最小、相关系数最接近1，是预测精度最好的算法。

4.2 基于SSVR的车速预测问题中参数寻优算法对比分析

采用实验1的数据，分别使用网格搜索方法(GridSearch)、遗传算法GA、布谷鸟搜索算法(CSA)对SSVR的参数进行寻优，其中，GA训练参数最大进化代数为200，种群最大数量为100，交叉概率为0.9，C的取值为[0.1,100],g的取值为[0.1,100]；CSA训练参数的最大代数为200，交叉概率为0.25，C的取值为[0.1,100],g的取值为[0.1,100],寻优结果对比见表3。

Table 3 Analysis result comparison amongGS,GA and CSA in experiment 2

可以看出，虽然网格搜索方法所用时间很短，但是采用其定参之后的预测结果的均方根误差与相关系数相较另外两种算法差距较大，可以认为精度较低，结果不可靠；而布谷鸟算法寻优结果与遗传算法寻优结果相比，精度略有提高，所用时间却快很多。

因此，在基于SSVR的车速预测实验中，布谷鸟算法是一种比较好的参数寻优算法。

Figure 3 Traffic state forecasting result图3 交通状态预测分析结果图

4.3 交通状态预测分析

根据基于CSA-SSVR的交通状态预测模型，从实验1的350组训练数据中随机删除5%，使用基于CSA-SSVR的交通状态预测模型对未来的100组交通状态进行预测，输出的预测结果与实际值如图3所示。

本实验中，在数据存在部分缺失的情况下，该模型预测的准确性约为97.5%，对于未来交通状态预测准确度较高。

5 结束语

对交通状态的预测在交通控制、交通安全与汽车节能方面具有重要意义。本文根据移动群智感知采集到的位置与速度信息，通过对路段车速的预测推导出路段交通状态的变化情况。由于SVR在处理非线性数据的预测问题上精度较高，结合城市道路交通信息具有一定周期性的特点，提出了CSA-SSVR。通过与其它方法的预测效果进行对比，说明了它在车速预测方面具有更高的精度。然后针对移动群智感知环境下容易出现的数据缺失的情况，提出了数据补齐方案，建立基于CSA-SSVR的交通状态预测模型，为移动群智感知环境下交通状态的预测提供了一个有效的模型。