基于SLIC的自适应多主体图像分割算法

郭 伟，李红达，邢宇哲

(辽宁工程技术大学软件学院,辽宁 葫芦岛 125105)

1 引言

图像分割是按照一定的相似性准则把图像划分成一定数量区域的过程，图像分割是图像处理的前期阶段，在实际的处理中有着非常广泛的应用，已在目标识别、模式识别、人工智能等众多领域得到了普遍的应用。

目前，图像的尺寸越来越大，直接在像素粒度层面上对图像进行处理的计算效率较低，这就要求减少像素数量，扩大像素所代表的含义。2003年，Berkeley大学机器视觉实验室的Ren等人[1]第一次提出了超像素这个概念，所谓超像素，是指具有相似纹理、颜色、亮度等特征的相邻像素构成的子区域。超像素分割就是把像素聚类成超像素的过程。它通过像素的聚合保存了图像的边界信息，降低了后续图像处理的复杂度。超像素分割算法加速了图像处理的速度，并很好地保留了边界信息。Moore等人[2]提出的SL(Superpixel Lattices)算法采用Canny边界检测算法获得原始图像边界，再不断地在垂直和水平两个方向寻找最优路径把图像分割成超像素。Bergh等人[3]提出了SEED(Superpixels Extracted via Energy-Driven Samplin)算法，该算法不断修正网格元素的超像素边缘点，最终得到分割结果。简单线性迭代聚类算法SLIC (Simple Linear Iterative Clustering)是在CIELAB彩色空间的X-Y坐标下的五维特征向量，把N个像素点聚类成K类。相比于其他超像素分割算法，该算法分割速度快，能形成形状规则、大小均匀的超像素[4，5]，该算法的时间复杂度仅为O(n)，在处理高分辨率图像时可以减少时间复杂度，而且分割的数目和边缘贴合度是可控的。

超像素图像分割实际上是一种图像的过分割，没有实际的应用意义。在它基础上的图像处理成为了很好的研究方向，目前在图像分割、目标检测、特征提取、目标跟踪、人体姿势估计等方面都有了很好的发展。杨赛等人[6]提出一种基于超像素的显著性目标检测算法，先计算目标先验概率显著图，在超像素区域内建立词袋模型，算出条件概率显著图，把两种概率融合获取显著性目标。张雷等人[7]提出一种基于超像素的在线目标分割算法，结合上一帧的先验知识估计当前帧的外观模型，以超像素为节点构建马尔科夫模型，结合外观模型和马尔科夫模型构建能量最小化问题，应用图割方法计算分割结果。刘大千等人[8]提出一种基于超像素的局部模型匹配目标跟踪算法，利用前几帧的超像素块建立目标模型作为匹配模板，采用期望最大化EM(Expectation Maximization)估计前景信息，与局部图像匹配确定跟踪目标。韩守东等人[9]提出一种快速图像分割算法，该算法用超像素作为图模型的节点，用Graph Cut模型实现加速，获得分割结果。Levinshtein等人[10]提出一种基于超像素的特征提取算法，首先用超像素构建图节点，利用先验知识预测每个点的隶属度，不断迭代更新，确定一个封闭的轮廓逼近特征图像。Mori[11]提出了一种基于超像素的人体姿势估计算法，该算法用超像素作为节点，大大减少了图像中人体关节点搜索的数目，同时应用超像素算法使用一侧的躯体来预测另一半的躯体特征，降低了算法的复杂度。

多主体图像分割区别于传统的图像分割，传统的图像分割是分别出前景和背景，主要提取前景，忽略背景。多主体图像分割不是简单地分别出前景和背景，而是一副图像本身具有多个主体，每个主体的重要性不分大小，都有实际的意义，需要把每一部分都分离出来，因此多主体图像分割也引起到了各方面的关注。纪则轩等人[12]提出一种无监督的模糊C均值FCM(Fuzzy C-Means)算法，结合Gabor滤波器对像素的纹理信息进行处理，有很强的适应性，算法仅需要一次聚类，但在前期对纹理处理的过程中需要对相位、方向角、频率同时求解，增大了算法的复杂性。余卫宇等人[13]提出一种对图像分块的思想，对不同区域的图像采用不同的阈值，结合蚁群算法对图像进行分割，算法虽然对细节处理较好但容易出现过分割现象，且需要迭代多次。Tao等人[14]将像素信息利用Graph Cut算法转化为图结构，计算其中的最小割， 对于每个像素根据其最小割边的位置赋予对应的标记，算法提高了边界分割率但效率较低。伯彭波等人[15]在文献[14]的基础上提出一种交互分割的方式，首先通过超像素对图像进行预处理，再利用Graph Cut算法构建多层流网络，最后根据用户提供的图形信息得出分割结果 。这种算法可以利用用户的交互给出最符合用户需要的解决方案，但在实际中并不允许用户的实时交互，而且适应性不够。Grady[16]利用Random Walk算法计算每个像素属于用户标记主体的可能性，不断更新隶属度矩阵，是一种交互分割算法。

本文在超像素和密度聚类算法的基础上提出了一种基于SLIC的自适应DBSCAN(Density-Based Spatial Clustering of Applications with Noise)多主体图像分割算法。在本文之前已有对SLIC和DBSCAN算法结合用于图像分割的研究。Wu等人[17]提出了一种SLIC结合DBSCAN算法用于分割巡检图像的算法，胡峻峰等人[18]提出了一种SLIC结合DBSCAN算法用于分割木材表面缺陷的算法，凌朝东等人[19]提出一种SLIC结合DBSCAN算法用于解决眼底图像硬性渗出检测的算法。上述三种算法都是对专一图像进行分割，每一个算法都有其自己独立的参数，并不具有普遍适用性，对于不同的图像并不能做到同时适用。因此，本文提出一种自适应参数算法用于解决不同图像之间参数不同的算法。本文使用SLIC算法和DBSCAN算法结合用于处理图像分割问题，其中SLIC算法可以提高算法效率，而DBSCAN算法可以发现任意形状的聚类，并且不需要确定聚类数目，再通过计算得到全局最优解，最后与SLIC、Meanshift、Kmeans、分水岭算法等传统算法和SLIC-Kmeans、SLIC-Meanshift算法进行比较 ，从精度和效率两方面对本文算法进行验证和评价。

2 SLIC超像素图像分割

SLIC超像素分割算法是Achanta等人提出的一种实现方便、思想简单的算法，它将RGB彩色空间的像素点转化为CIELAB彩色空间的X-Y坐标下的五维特征向量Pi=(li,ai,bi,xi,yi)i=(1,2,…,N)，将其中的N个像素点通过局部聚类形成K个超像素区域。

SLIC算法具体实现步骤如下：

(1)初始化聚类中心。

为了避免初始种子点落在图像的边缘，将初始种子点移动到当前种子点的3×3邻域内梯度最小的位置。图像的梯度计算公式为:

G(x,y)=‖l(x+1,y)-l(x-1,y)‖2+

‖l(x,y+1)-l(x,y-1)‖2

其中,l(x,y)是超像素di=(xi,yi)的位置向量，‖·‖是矩阵的二范式，由此获得初始种子点的颜色向量Ci=(li,ai,bi)，因此确定初始种子点的表达向量pi=(Ci,di)，i=1,…,K。

(2)相似度度量。

SLIC的相似度度量方法如下:

其中，dlab为像素点之间的色差，dxy为像素点之间的空间距离，D(i,k)为像素点i与聚类中心k之间的相似度，D(i,k)的值越小，说明两者越相似，m∈1,40为调节颜色距离的权重。

(3)迭代更新聚类中心。

在聚类中心的2S×2S范围内确定每一个像素点的归属，把归属于一类聚类的像素点的五维向量值求平均获得更新后的聚类中心，重复此过程直至迭代完成。

(4)对每一个归属于同一聚类的像素点赋予相同的聚类标签，形成K个超像素。

对双边滤波之后的图像进行SLIC超像素分割，K的取值分别为100,400,3 000时得到如图1所示的分割图像。

Figure 1 SLIC super-pixel segmentation images under different K values 图1 不同的K值下SLIC超像素分割图像

3 DBSCAN算法聚类和自适应算法

3.1 DBSCAN算法

DBSCAN 算法是一种经典的基于密度的聚类算法，可以自动确定聚类的数量，能够发现任意形状簇，只需要一次迭代，聚类速度比较快，DBSCAN具体算法参照文献[20]。

DBSCAN算法有两个重要的参数Eps和MinPts，分别为聚类中心的最大差异和聚类的最小数量。实验表明，该算法对参数有着较强的敏感性，参数的设定严重影响着实验的结果，而且对于不同的图像需要设定不同的参数。

由图2可以看出，对于一幅图像来说不同的参数对图像分割的影响很大。对于上下两幅图来说，同样的Eps值，图2b在Eps=500时可以很好地分辨出整体轮廓，而图2e却出现过分割现象；当Eps=2300时，图2c出现欠分割现象，而图2f却能很好地分割出主体；由图图2e也可以发现整体参数对局部影响很大。因此，需要提出一种自适应的参数算法以适应不同图像的要求，同时也要满足对于同一幅图像不同位置的要求。

3.2 自适应算法

DBSCAN算法对Eps和MinPts有着很强的敏感性，分割不同的图像需要采取不同的参数值，因此自适应获取参数值就成为了DBSCAN算法的重点。有关DBSCAN的参数选择问题，已经有了大量的研究，但大部分的研究都是针对数据的分类问题，图像有其独特的性质，对于颜色的敏感性更高，距离只是辅助判断。因此，图像分割更关注像素之间的颜色差异而非距离，本文使用的DBSCAN算法只对比全局颜色信息，并不计算像素之间的距离信息，可以减少空间信息对分割效果的影响，自适应地获取参数可以取得良好的效果。

首先我们需要解决Eps的选取问题。本文选取文献[21]的主要方法，通过对比全局超像素颜色信息自适应地决定Eps值。

自适应DBSCAN算法的主要步骤如下：

(1)计算全局距离分布矩阵DIST。

DISTn×n={dist(i,j)|1≤i≤n,1≤j≤n}

其中,n=D，D表示超像素分割后的聚类中心组成的数据集，DIST是n行n列的对称矩阵，dist(i,j)表示第i个超像素中心到第j个超像素中心的距离。

(2)对每一个DIST排序并转置得到顺序矩阵:

KNN0n×n=sort(DISTn×n)′

KNN0n×n的每一列向量代表数据集中每个超像素到最近的k(k=1,…,n)个超像素的距离集合。由于每一列向量的第一个元素都是0，对后续处理影响很大，因此整体删除第一行，从第二行开始算起，得到新的矩阵KNNn×(n-1):

KNNn×(n-1)=sort(KNN0n×n(1:end;2:end))

KNNn×(n-1)的第k(k=1,…,n)列即为数据集中超像素k最近邻域集合DISTk，对于KNNn×(n-1)绘图得到图3，其中图3a为全部超像素与其他超像素的距离，图3b为单个超像素与其他超像素的距离，图3c为图3b曲线的概率密度图。

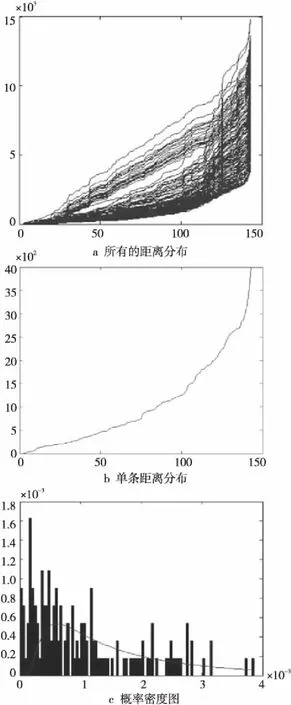
Figure 3 Distance distribution of super-pixels图3 超像素的距离函数分布

由图3a可以看到，随着k的增加函数上升，即DIST(n,k)≤DIST(n,k+1),从中取出单个对象的函数图像如图3b所示，概率密度直方图及概率密度曲线如图3c所示。

(3)寻找图3c中概率密度曲线的最高点，即与超像素中心最相近的点，保证大多数的邻接超像素可以聚集在一起，使用统计模型进行拟合，通过实验发现使用逆高斯密度分布拟合的效果比较好，逆高斯密度分布的概率密度公式为：

其中,λ和μ可以使用极大似然估计得到。为了获得最高点的值，解方程dP(x)/dx=0,得到一个整数解：

因此，对于每个点k，根据逆高斯概率密度函数得到：

对于不同的超像素k使用不同的Eps(k)值，可以极大地保证超像素总是向着密度最大的方向靠拢，当两个超像素之间的差值超过Eps(k)时，扩散结束。

所有的超像素点遍历完成后，每个聚类的聚类数目也同时被计算出来，这里并不存在最小的聚类数目，对于超像素来说，每一个超像素都有可能是孤立的聚类中心，因此MinPts的值也可以自适应确定，并且MinPts参数对本文算法的影响较小。

遍历完所有像素后，超像素划分为两类：具有实际意义的超像素聚类和被划为噪声点的聚类。但是，被划为噪声点的聚类有可能是多主体分割的一部分，却被视为孤立点，不应该被单独分离出来，因此应进行孤立点检测，并更新聚类内容和聚类数目。

3.3 孤立点控制

算法中超像素的自适应Eps值会把噪声点排除到聚类之外，或者聚类中心的超像素与邻接超像素有较大差异，并没有邻接超像素一起组成聚类，单独化为一类，这些孤立点主要有以下几个形成原因：它们与数据的其他部分不一致；由于度量或执行错误导致孤立点产生；也可能是固有数据变异性的结果。但是，这些噪声点同样是图像聚类的一部分，为了解决这一问题，本文将孤立点的合并放到了超像素聚类之后，利用聚类数目判断孤立点，并进行融合。

定义1(聚类可达密度lrd(O)) 用Cu(O)表示聚类O的所有所属超像素，reach_distO,p表示对象p与聚类中心O的可达距离，CuO表示聚类个数，那么聚类O的可达密度为聚类中心与它的所属超像素的平均可达距离的倒数：

定义2(局部异常因子LOF(p,O))O表示与对象p相邻的聚类，lrdO表示不包含p对象的聚类可达密度，lrdO1表示包含p对象的聚类可达密度,Am表示所有与p相邻的超像素集合,则:

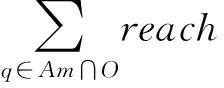
LOF同时反映聚类内部与邻接超像素的异常状况。如果p可以被归类为聚类的一种，则对后半部分影响较大，如果是一个孤立点，则对前半部分影响较大。LOF越小，说明对象p对于聚类O的异常影响越小。聚类中心和邻接超像素与对象p越相似，LOF越小，如果p不是孤立点，则LOF接近1，如果p的所有邻接聚类的LOF均大于1,则p被作为孤立点处理，如果局部异常因子均小于1，则最终选取影响因子最小的聚类为它的目标聚类，如图4。

Figure 4 Outlier control process图4 孤立点控制过程

本文算法自适应地确定Eps和MinPts，避免了DBSCAN的参数敏感性，增强了算法的鲁棒性。自适应选取Eps使每个超像素朝着最相似的超像素聚类，极大地减小了全局的Eps对图像细节的影响，保证分割的结果既能分出主要的区域，还能在细节处理上优于其他的算法。

4 实验结果分析

实验平台：本文算法运行的操作系统为Windows 7，Intel(R) Core(TM) i5-2450M，2.5 GHz，在Matlab2012a上实现。

数据集：本文实验所用的数据集为Berkeley benchmark500标准数据集[22]。每幅图像的大小为481×321，分割的超像素个数为400个，紧密度系数m对实验结果影响不大，算法运行时间在紧密度系数m发生变化时有轻微抖动，抖动幅度小于5%，算法运行平稳，实验选取边界分割率最大的20组实验数据取平均值，确定紧密度系数m取值为20。

图像分割评价标准：概率随机指数准则PRI(Probabilistic Rand Index)，取值为[0,1]，PRI越大代表结果越好。信息变化指数VOI(Variation of Information)，取值为[0,∞)，VOI越小代表分割结果越好。

本文从分割效果、分割时间以及与人工分割的结果进行比较，验证算法的有效性。

4.1 超像素粒子度与分割结果的关系

本文算法的分割效果与分割时间严重依赖于超像素的个数。如果分割个数过少，则缺少边界信息，边界检测率低，对图像细节处理不理想；如果分割个数过多，不能保证后续处理的时间效率，造成浪费。超像素个数与边界检测率的关系和超像素个数与分割时间的关系如图5所示。

Figure 5 Effect of the number of super-pixels on segmentation图5 超像素个数对分割算法的影响

由图5a所示，超像素图像分割在超像素个数为400时可以达到99.67%的检测率，完全可以检测出绝大多数的图像边界，不存在欠分割现象，而当超像素个数大于400以后，边界分割率并没有较明显的提升，只是在细微之处存在修改，并不影响图像分割的整体效果；而由图5b所示，超像素个数对超像素分割时间并没有影响，但对于后续的图像分割程序有着较明显的效果，在超像素个数为1 000以下时,图像分割算法时间并没有大幅度的提升，当超像素个数大于1 000时便出现了较大幅度变化，成指数趋势增长。综合图5两幅图，本实验采取的超像素个数为K=400，既可以保证有很高的边界检测率，而且也保证了算法的时间成本没有较大幅度增加。

图1同时给出了不同超像素个数的不同分割结果(对于像素个数为512×512的Lena图像分别分割为100、400、3 000的分割结果)。从图1中可以观察到，在超像素个数K=100时，虽然基本反映出图像的边界，但仍有部分边界不能很好地分割出来，边界分割率低，影响后续处理效果，如果增加超像素的个数为K=3000，则大幅增加了图像分割的时间，最终确定为超像素个数为K=400，减少了后续分割的空间占用和时间花费。

4.2 分割效果

本节对SLIC、Meanshift、Kmeans、分水岭等传统算法和SLIC-Kmeans、SLIC-Meanshift算法进行分割效果比较，比较结果如图6所示。

(1)分割结果对比。相对于传统的分水岭算法、Kmeans算法、Meanshift算法，本文算法避免了图像的过分割现象，利用超像素的处理提高了分割的精度，利用DBSCAN算法在全局搜索更优参数，进一步提升了精度。如表1所示，SLIC-Kmeans算法与传统算法相比PRI提升很高，与传统Kmeans算法相比,算法PRI提高28.07%，而VOI降低71.09%，说明SLIC对图像的噪声有很强的抑制作用，而本文算法相较于SLIC-Meanshift算法和SLIC-Kmeans算法，DBSCAN算法能发现更适合图像分割的聚类，可以进一步寻找到不同形状的聚类，发现更优的分割参数。VOI指数用来计算算法分割结果与人工标注结果的差异性，VOI值越小,说明算法的分割结果越接近人工分割的结果。对比其它几种算法，本文算法利用DBSCAN算法对超像素聚类更符合人类的分割特点。SLIC算法作为本文算法的基础，会出现严重的过分割现象，Kmeans算法受初始点的选择影响较大，Meanshift对简单图像分割结果较好，对于复杂图像会出现欠分割现象，分水岭算法、Meanshift算法易出现局部最优的结果，造成分割不准确的现象。

Figure 6 Results comparison among different segmentation algorithm图6 不同分割算法的结果对比

算法评价指标PRIVOISLIC0.198 19.725 1Kmeans0.650 11.272 3分水岭0.574 31.240 2Meanshift0.564 71.439 6SLIC-Meanshift0.727 10.587 2SLIC-Kmeans0.832 60.367 7本文算法0.889 70.228 4

(2)分割时间对比。相较于SLIC算法，本文算法分割时间增加了后续的处理时间，但由于超像素的预处理过程使得后续处理的目标数量大大减少，因此总的分割时间并没有明显增加，主要的时间影响在于孤立点处理部分。

本文算法运行时间分成三部分：超像素分割阶段、聚类阶段和孤立点控制阶段。三个阶段时间相加就是算法分割时间。表2给出了图6中三幅图像的运行时间。从表2可以看出，对于一幅481×321的图像，分割时间大概需要1.5 s，且不需要人工交互，增强了算法的适应性。

Table 2 Algorithm running time

与图6其他的几种算法相比，分割时间如表3所示。本文算法优于传统的分水岭算法、MeanShift算法、SLIC-Meanshift算法、SLIC-Kmeans算法，但运行时间高于SLIC算法和Kmeans算法。对比表3中的Kmeans算法、MeanShift算法、SLIC-Kmeans算法和SLIC-Meanshift算法，算法时间大大缩短，说明SLIC对加速图像分割有很好的效果。本文算法时间优于SLIC-Meanshift算法和SLIC-Kmeans算法的，说明DBSCAN算法无需迭代的优越性，图像能够快速分割。

Table 3 Running time of different algorithms

5 结束语

本文针对多主体图像分割的交互问题提出了一种基于SLIC超像素的DBSCAN自适应图像分割算法。算法使用SLIC超像素分割算法把图像分割为超像素点 ，再通过自适应的DBSCAN算法进行聚类操作，得到多主体分割结果。相对于已有方法，本文算法可以自适应地获取多主体的分割数目，不需要人工交互，减少了用户的操作流程，增加了算法的适应性，在各种评价指标上也有很好的效果。

实验显示了相对于其他算法的分割效果和分割效率，本文算法可以快速得到多主体图像分割结果。在未来的工作中将研究先确定聚类数目，给每一个种子点增加一个隶属度矩阵，再确定分割边界的方法。