高层住宅建筑风荷载特性及风致响应

2018-08-22王腾飞邹良浩

土木工程与管理学报 2018年4期

王腾飞，邹良浩，孙艳

(1. 武汉科技大学城市建设学院，湖北武汉 430065； 2. 武汉大学土木建筑工程学院，湖北武汉 430072)

随着经济社会的发展，城市化进程不断加快，城市建设用地供应日趋紧张，高层住宅建筑得到了快速发展，在城市中产生了密集的建筑群，导致风场环境复杂，由于相邻建筑物之间的流场干扰，受扰高层建筑的风荷载与风致响应与单体相比有较大的变化，某些情况下可能大大超过单体的情况，引起抗风设计中的安全问题[1～5]。随着生活水平的不断提高，对居住品质要求也越来越高，例如住宅采光、通风和空间等成为购房重要的关注点，但建筑结构设计时往往与规范[6]建议不能兼顾，从而产生了很多体型不规则的高层住宅建筑，同时随着新型建筑材料的应用，高层建筑的阻尼变小，结构柔度变大，对风荷载更加敏感，使得风荷载逐渐成为结构的安全性和舒适性的控制荷载[7,8]。目前荷载规范[9]针对上述问题给出了设计指导，但鉴于实际风场环境和结构体型比较复杂，规范尚不能完全指导此类结构的抗风设计，根据标准[10]建议应采用风洞试验，部分学者基于风洞试验对此类结构风荷载与风致响应进行了分析并提出了设计建议[11～13]，但相关研究仍有待进一步补充。

某住宅项目有一栋复杂体型的超高层建筑，建筑高为183.65 m，平面尺寸为40.9 m×19.4 m，高宽比为6.51，四面均有凹角，主体大致呈“凹”形，结构采用钢筋混凝土剪力墙结构形式，同时周边存在多栋已建或待建的100 m以上的高层建筑，风场环境十分复杂。基于上述情况，本建筑属于结构体型复杂，对风荷载比较敏感的高层建筑，且周边建筑干扰效应明显，荷载规范对此建筑的抗风设计适用性有限，为了准确评估结构的抗风性能，基于刚性模型测压风洞试验分析了结构的风荷载与风致响应，为了进一步研究体型和周边建筑干扰对结构风荷载与风致响应的影响，增加了三组不同高宽比单体工况进行对比分析，并与规范比较，得出了一些有意义的结论，所得结论可为类似工程的抗风设计提供参考。

1 风洞试验

试验刚性测压模型由工程塑料制成，具有足够的强度和刚度，几何缩尺比为1∶200。模型布置了483个测压点，主体各测点层均布置26个。测压管路与电子扫描阀相连，对模型分别进行同步测试。模型底部与连接板固连，连接板与风洞试验段工作转盘固连。为考虑邻近建筑物的干扰影响，试验模拟了周围约250 m范围内的主要建筑，定义为工况a，并补充了无周围建筑时三种工况试验，各工况列表如表1所示，风洞试验模型如图1(图1a中左侧为目标建筑1#)所示，建筑相对位置和风向角定义如图2，其余三种工况风向角定义同工况a。

表1 风洞试验工况

图1 风洞试验模型

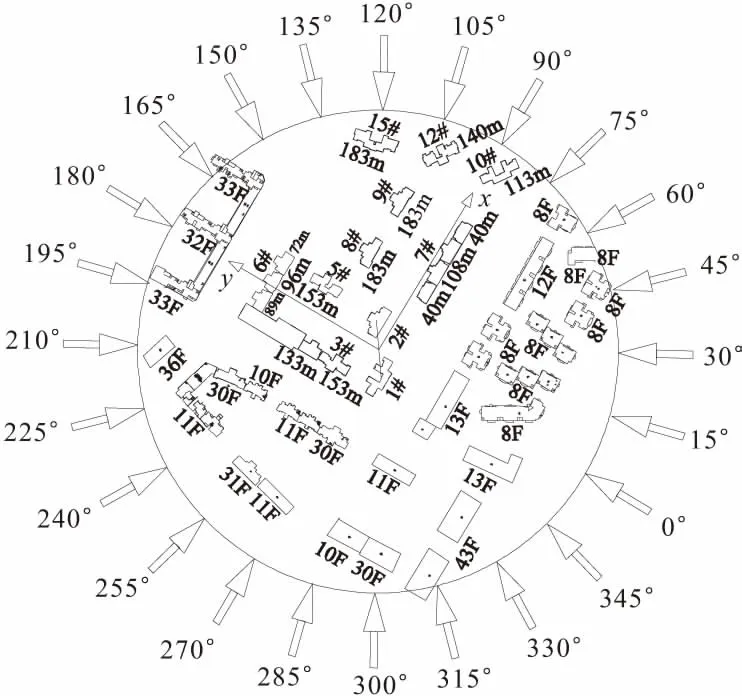
图2 建筑相对位置和风向角定义

本试验在武汉大学WD-1风洞试验室中进行，该风洞试验段长×宽×高=16 m×3.2 m×2.1 m，试验风速由1 m/s至30 m/s连续可调。通过风洞试验段上游设置的尖劈、粗糙元组合能准确地模拟不同缩尺比的大气边界层风场特性。直径2.5 m的自动控制工作转盘可以模拟0～360°任一风向角的模型试验风场，建筑所处地貌为我国建筑结构荷载规范中的C类地貌，故模拟风场的风剖面地面粗糙度指数α=0.22。所模拟风场的风剖面、紊流度和风速谱见文献[14]。

2 试验数据处理

本试验通过旋转工作转盘，模拟0～360°风向角的情况，其角度间隔为15°，共24个试验风向角，脉动压力的采样时间为60 s，每个测点的采样频率为331 Hz，试验参考点高度为0.925 m(与模型顶部同高)，试验参考点风速为9.5 m/s。为方便计算说明，各轴向定义如图3。

图3 主体结构平面尺寸和坐标/mm

2.1 整体风力系数计算

根据采样得到的各测点风压时程，各测点风压平均值按下式计算：

(1)

式中：n为测点采样点数；wi为j测点在i瞬时的风压值。结构某点的平均风压系数为：

(2)

式中：Vj为测点j高度处平均风速；ρ为空气密度。风场风剖面风速换算公式为：

Vj=Vhf(hj/hf)α

(3)

由此可以得到测点j的平均风压系数表示为：

(4)

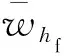
为便于和规范对比，利用计算得到的各测点平均风压系数，采用面积加权的方法计算了各工况沿x和y轴向各层测点高度处的平均风力系数，将各层高度处的平均风力系数取平均值可得到整体平均风力系数，具体由如下公式计算。

结构x轴向和y轴向第q层平均风力系数计算如下：

(5)

(6)

式中：N为第q层的测点总数；μspq和Bpq为第q层的第p测点的平均风压系数和控制宽度；αpq为第q层的第p测点所在平面法线负方向与x轴向正方向夹角；Bx(q)和By(q)分别为结构在第q层测点高度处截面x轴向和y轴向投影宽度。

在得到各轴向各层风力系数以后，各轴向整体风力系数由如下公式计算：

(7)

(8)

式中：M为计算测点层数；Hq为第q层测点折算高度。

2.2 风致响应计算

本文风致响应计算方法采用文献[15]中的频域计算方法，首先由模型各层测点风压时程得到模型各层的三维风荷载时程曲线，再通过傅里叶变换，分析处理得到模型各层三维风荷载谱密度矩阵，经相似变换得到实际结构各层风荷载的自、互谱密度，然后利用有限元分析得到的质量和动力特性，根据随机振动理论计算得到结构各层的最大加速度和动态位移响应。限于文章篇幅，计算过程此处不再赘述。

计算时取100年一遇基本风压0.40 kN/m2，加速度响应计算阻尼比0.02，位移响应计算阻尼比0.05，峰因子取为2.5，不同高宽比结构各轴向前两阶振型频率列表如表2。

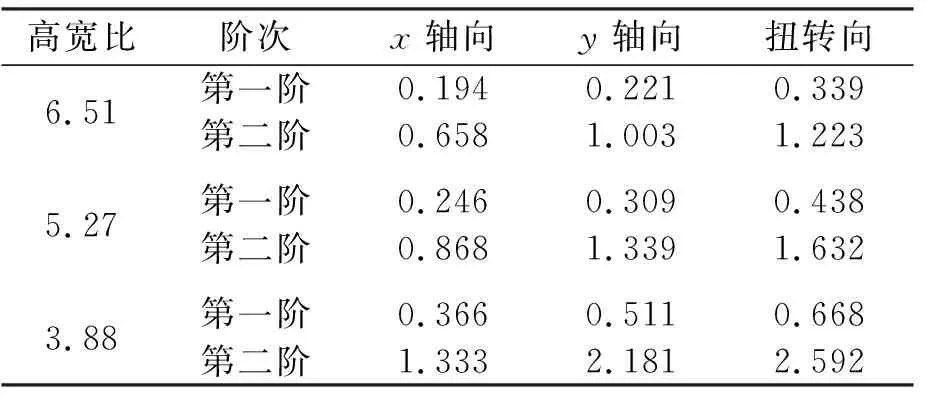
表2 结构固有频率 Hz

3 试验结果分析

3.1 整体风力系数

图4分别给出了住宅楼各工况的轴向整体风力系数沿风向角的变化折线图，对比a，b两种工况，对于x轴向，图4a表明，两种工况风力系数值相对波动十分显著，特别是在120°风向角，偏离差达到1，其主要原因是工况a下在来流方向存在与其等高的2#，8#，9#三栋住宅等建筑，“遮挡效应”显著，使其值减小；对于y轴向，图4b表明，两种工况μs随风向角变化趋于一致，除个别风向角外，90°风向角后偏离相对明显，其原因是0～90°风向角结构来流方向无较高建筑，90°风向角后结构来流方向周边建筑遮挡显著，最大偏离值约0.5(315°风向角)，综合分析说明周边建筑的存在对x轴向μs干扰更为显著。为了更好地探究高宽比对μs变化的影响，对比三种工况b，c，d可知，结构μs沿风向角的变化趋势基本一致，随着高宽比增大结构μs变化规律不明显，d工况下值整体略小，偏差最大为0.22(x轴向315°风向角)，所在风向角非最不利风向角，几乎可以忽略。

图4 整体风力系数随风向角的变化

由于此住宅楼结构体型复杂，规范未能直接涵盖此类结构，本文以荷载规范[9]建议的矩形截面高层建筑体型系数取值作为参考。根据荷载规范，结构长宽比约为2，x轴向迎风时可取值1.2，y轴向迎风时可取值1.4；工况a下x和y轴向μs最大值分别出现在45°和345°风向角，值分别为0.88和1.42；工况b下最大值分别出现在60°和180°风向角，值分别为1.11和1.52，由分析可知，两种工况y轴向超出规范建议值，x轴向均小于规范值，可见对此结构应加强y轴向风荷载设计。

综合分析来看，此复杂体型结构风荷载取值不宜直接采用规范矩形截面建议值，应参考类似条件风洞试验资料或采用风洞试验确定。

3.2 风致响应

3.2.1加速度响应

根据上文所述风致响应计算方法，可以计算得到各工况下结构各层最大加速度响应，本文着重分析最高居住层(工况a和b为169 m处，工况c和d分别为133 m和94 m处)的加速度响应随风向角变化。图5分别给出了住宅楼各工况下最高居住层最大加速度响应沿风向角的变化折线图。对比a，b两种工况，对于x轴向，图5a表明，工况a与b相比加速度响应具有明显的波动，但其值均较小，实际相差并不大，最大偏离发生在330°风向角，偏离值约0.023 m/s2；对于y轴向，图5b表明，最大偏离发生在105°风向角，偏离值约0.053 m/s2，其主要原因是在105°风向角时，工况a下结构来流方向存在2#，8#，9#(高183 m)和12# (高140 m)高层住宅建筑的遮挡，使得脉动风荷载较小，两种工况加速度响应最大值均发生在255°风向角，值分别为0.115 m/s2和0.118 m/s2，差值较小，根据高规[6]3.7.6条规定，10年一遇的风荷载标准值作用下住宅建筑加速度限值为0.15 m/s2，可见结构平动舒适度满足规范要求。对于扭转向，最大角加速度响应最大偏离也发生在105°风向角，两种工况加速度响应最大值分别发生在135°和105°风向角，值均为0.0044 rad/s2。

图5 最高居住层最大加速度响应随风向角的变化

对比b，c，d三种工况，各向风向角加速度响应均随着高宽比的增大而增大，相邻高宽比结构加速度响应最大值增大分别为94.87%和58.37%(255°风向角y轴向)，b，c工况响应随风向角变化趋势相近，幅度较大，d工况由于高宽比较小，响应变化幅度显著减小。对于各工况x轴向，以沿主轴向四个风向角进行分析可知，x轴处于顺风向(90°和270°风向角)时，两种工况加速度响应值相差极小，x轴处于横风向(0°和180°风向角)时，两种工况加速度响应值相差相对较大，可见高宽比增大使得结构横风向加速度响应增加较显著。y轴向为结构平动加速度响应的控制轴向，各风向角变化幅度均较大，但在主轴向仍表现出同上所述规律。

规范[9]通常考察结构沿主轴方向的响应，综合工况b，c，d分析可知，结构的加速度响应最大值并未出现在结构的主轴顺风向和横风向，而是偏离了一定角度，对于工况b和c，控制轴向y轴处于横风向(90°和270°风向角)加速度响应值比处于顺风向(0°和180°风向角)时的大，工况d由于高宽比较小，值均较小，表现不明显，进行抗风设计时应注意。

3.2.2位移响应

图6分别给出了住宅楼各工况的最高居住层最大位移响应随风向角的变化折线图，对于工况a和b，对比图4可知，位移响应与整体风力系数的绝对值走势基本相同，这说明位移响应中由平均风荷载产生的静态位移响应占主导，但由于动态位移的变化，结构位移响应最大值发生的风向角有变化，工况a时，x轴向位移响应最大值发生在240°风向角，相比结构μs的有变化，值为0.059 m，其值与工况b基本一致；y轴向位移响应最大值发生在345°风向角，值为0.116 m，工况b时，位移响应的最大值发生在165°和180°风向角，为0.114 m；对于扭转向，105°风向角有明显偏差，其原因同上，两种工况位移响应最大值分别发生在135°和105°风向角，值均为0.0009 rad和0.0011 rad。

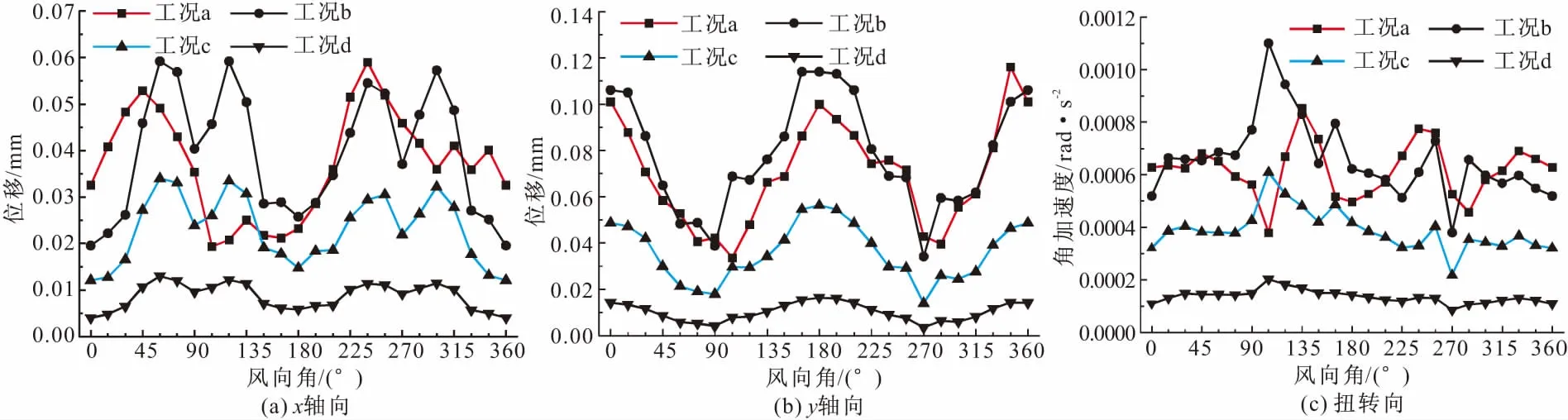
图6 最高居住层最大位移响应随风向角的变化

对比b，c，d三种工况，三个方向位移随风向角的变化规律基本一致，但是变化幅度明显减小，特别是工况d，变化趋势十分平缓。以控制轴向y轴向为例进行说明，三种工况下，结构顶部位移与结构高度之比最大值分别为1/1489，1/2365，1/5735，相邻之间比值为1.59和2.42，可见随着高宽比的增大结构位移比值增大显著，即结构位移响应增大显著。但与上述加速度响应不同的是，结构轴向位移响应的控制风向表现为顺风向(180°风向角沿y轴向)。