交叉验证的GRNN神经网络雷达目标识别方法研究

林悦，夏厚培

(1.南京信息工程大学 电子与信息工程学院，江苏 南京 210044；2.中国船舶重工集团公司 第七二四研究所，江苏 南京 211106)

0 引言

在雷达自动目标识别(automatic target recognition, ATR)技术中，对雷达目标高分辨距离像(high-eesolution range profile, HRRP)的研究最为广泛[1]。HRRP主要依托于宽带高分辨雷达获取目标多个散射中心点子回波在雷达径向方向上投影分布的矢量和[2]。目标的回波为与目标散射点分布相关的一维距离像，反映了在特定的雷达视角方向目标散射体雷达散射截面积(radar cross section, RCS)沿雷达视线方向散射点相对几何关系的分布情况[3]。

人工神经网络(artificial neural network, ANN)由于具有自适应能力，在识别领域中作为一种性能优良的分类器已被广泛应用[4]。广义回归神经网络(generalized regression neural network, GRNN)作为径向基函数神经网络(radial basis function, RBF)的一个重要分支，是一种基于非线性回归理论的典型前馈式局部逼近神经网络，通过激活神经元来逼近目标函数。GRNN具有良好的局部逼近性、全局最优性和较快的计算速度等优点。此外，网络中需要根据样本调整的参数只有一个光滑因子spread，因此能够避免人为因素对网络预测性能的影响[5]。

本文充分利用了GRNN局部逼近性能以及运算迅速的特点，将其作为分类器应用于雷达目标识别。此外，针对网络中需要人为调节的参数spread因子，本文利用交叉验证方法(cross-validation)改进了GRNN神经网络[6]，在选取最优的网络结构的同时，利用循环判别法筛选出适用于样本参数的光滑因子spread最优值，以达到对目标的最优识别效果。

1 目标距离像的数据预处理

在雷达自动目标识别中，对输入分类器的距离像样本数据的预处理至关重要。本文的预处理流程首先对原始距离像数据进行分角域建立模型，然后对数据进行加窗处理剔除周围冗余的噪声信号粗筛选，对距离像进行最大值粗对齐，再利用全局最小熵距离对齐算法对一维距离像完成精确对齐，最后使用归一化算法处理对齐后的数据。

1.1 全局最小熵距离对齐算法

全局最小熵距离对齐算法有良好的鲁棒性，且运算速度较快，能够实现对雷达目标回波距离像的精确对齐。该算法主要通过对距离像包络的幅度值运算，将平均距离像(average range profile, ARP)熵值作为对齐的标准，通过迭代求解法使熵值趋于最小，搜索其对应的位置来完成距离像的精确对齐[7]。

将距离像经压缩后的脉冲包络定义为p(r,n)，r表示距离，n代表回波信号的脉冲数序号，N为回波信号总数，Δ(n)表示当前第n个回波信号脉冲的偏移值，则可将ARP定义如下

当各回波信号未对齐时，其相应距离的信号幅度值相加所得的合成波形会因为各信号的波峰波谷相互错开相加发生钝化，此时检验回波信号是否对齐的问题就转化为求解ARP波形的锐化度大小，由此可得各个波形与原始位置的偏移量Δ(n)。波形锐化度可以使用信息熵来量化衡量，当合成波形的熵最小时，可以认为各个回波信号已经完成对齐处理。根据信息熵的定义，ARP的熵可以定义为[8]

对式(2)求导可得ARP熵的最小值

将式(1)代入，则有

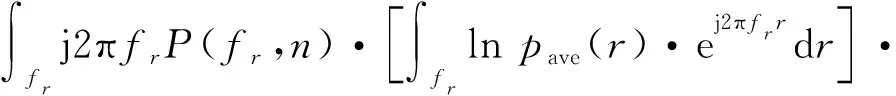
(4)

根据傅里叶变换的微分性质，式(6)可以表示为

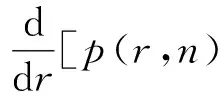
(6)

重复迭代对所有的脉冲进行移位并不断更新ARP，使其熵逐渐逼近全局最小值不再减小时，所得到的Δr(n)每次回波信号所需移位的偏移最终估值。由于式(6)中卷积运算可以利用FFT求解，因此全局最小熵距离对齐算法比传统的相关对齐法运算速度较快。算法流程图如图1所示。

1.2 归一化处理

高分辨距离像x(n)在距离像空间中是一个矢量点，其任意正倍数kx(n)(k>0)同样表示这个距离像。针对HRRP幅度敏感性的问题，一般用归一化的方法处理，使所有类别目标的距离像具有统一的尺度，方便待测HRRP样本与模版之间在尺度上比较。本文采用能量归一化方式，即每幅距离像x(n)对其总能量进行归一化处理，表达式如下

2 广义回归神经网络GRNN模型

广义回归神经网络(GRNN)由 Donald F. Specht 在1991年提出，它建立在数理统计非线性回归法的基础上，根据样本数据逼近其间隐藏的映射关系[9]。GRNN通过激活神经元来逼近目标函数，在局部逼近、全局最优及分类性能上比RBF具有更强的优势。网络收敛于数据样本量聚积较多的优化回归面，当样本数较少或样本数据不稳定时，回归预测效果十分明显[10]。此外，对于具体的网络样本训练而言，GRNN更显著的优势在于整个网络中需要根据样本数据调整的参数只有一个光滑因子spread，因此可以更快地预测网络且能在最大程度上避免人为因素影响，网络的学习全部依赖于输入的样本数据[11]。

2.1 GRNN的网络结构

GRNN网络结构如下图2所示，由4层模块组成，输入层将输入样本数据传递给模式层，其神经元数目与需要学习的输入样本中向量维数相同；数据通过模式层中各自对应的n个神经元传递函数处理后进入求和层；求和层中使用2种不同的神经元对输入数据加权求和；输出层中各神经元将求和层中处理后的数据相除，最终得到输出结果。

2.2 GRNN的理论原理

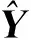
式中：n表示学习样本数据容量；p为随机变量x的维数；Xi，Yi为随机变量xi和yi的样本观测值；σ表示宽度系数，一般在神经网络中称作光滑因子spread，也就是网络的扩展速度。

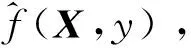
此时，根据神经网络的特性令

式中：Pi即为上图2中神经网络模式层第i个神经元的传递函数，其中X是神经网络的输入样本参数，Xi是第i个神经元所对应的学习样本参数。SD和SN则是神经网络求和层中2种神经元，SD负责对模式层所有神经元的输出值进行算术求和，连接权重值为1；而SN则是加权求和，权重值为输出样本Yi中各元素值。将上式带入，就可得到所对应的输出向量Y，即

GRNN模型只需要一个光滑因子σ参数所以结构简单，很大程度上减少了人为因素对模型参数选择的影响，因此网络结构的设计更加合理。从数学的角度来说，GRNN模型网络的优化实际上是参数σ确定的优化，找到了适用于网络的最优σ，也就能使经过网络训练后的样本输出值与实际值之间的均方差最小。参数σ取方法大多采用人工调整方法，存在着效率低、精度差的问题。

2.3 改进GRNN

针对GRNN神经网络光滑因子spread参数σ选择，本文采用了K重交叉验证法，根据最小均方误差(mean square error,MSE)寻找出的σ最优值，同时获得目标识别训练样本的最优输入输出值。

交叉验证(cross validation，CV)是数据分析时用来验证分类器模型性能的一种统计分析方法，基本思路是将数据重复使用以提高模型的精度，原理是将原始数据样本分组切割成较小子集，先在一个子集即训练集上作分析，再用其他子集即验证集或测试集分别用作选择模型和对学习方法的评估。交叉验证法主要的优点是将新数据代入训练好的模型时可以在一定程度上减小过拟合，并且可以从有限的数据中获取尽可能多的有效信息。

交叉验证法主要有以下3种方法：

(1) 简单交叉验证法：随机选取一部分样本为训练集，剩下做测试集，选择测试误差最小的模型。方法简单速度快，但浪费了部分数据，数据量较小时影响较大。

(2)K-重交叉验证法(k-folder cross validation，K-CV)：将样本数据集随机划分为k份，k-1份作为训练集，1份为测试集，依次轮换训练集和测试集k次[12]，验证误差最小的模型为所求模型，并将k次的平均交叉验证识别正确率作为分类器的性能指标。优点是所有的样本都被作为了训练集测试集，每个样本都被验证一次，结果更加客观，通常k取10也就是10重交叉验证。

(3) 留一法(leave one out cross validation，LOO-CV)：设原始样本数据集有N个样本，LOO-CV也就相当于K=N时的K-CV，即每一个样本都单独作为一次测试集，其余的N-1本作为训练集，所以LOO-CV会得到N个模型。优点是每个样本都用于训练模型，因此最接近原始样本的分布，且实验过程中没有随机因素的影响，评估所得的结果更加可靠。

上面3种方法中，LOO-CV评估结果是最客观可靠的，不过其计算成本高，运算时间长，在实际操作上很困难。综上，本文采用的是K-CV，其中k取10，即10重交叉验证法，算法的示意图如下图3。

本文将样本集随机划分为10份，其中9份作为训练数据，另1份作为测试数据，训练和验证10次。10次结果的正确率均值作为对算法精度的估计，具体方法如下：

(1) 将样本数据集S随机划分为10个不同的子集，分别记作S1,…,S10，每个子集中样本的数量为e/10个。

(2) 对于每个模型Ei，进行如下操作：使j从1至10循环；训练集为S1∪…∪Sj-1∪Sj+1∪…∪S10，训练模型为Ei，对应的假设函数为hij；验证集为Sj，得出泛化误差。

(3) 计算各模型的平均泛化误差，泛化误差最小的模型Ei即为系统的最佳模型。

本文选取均方误差(MSE)作为实验中的泛化误差，也就是神经网络的性能函数。若有n组样本数据，每组输入输出样本数据为[Pi,Ti],i=1,2,…,n，Yi为经网络训练后的输出数据，则MSE定义为每一组数据的误差平方和除以样本的总组数n式如下

3 系统仿真

为验证本文方法的有效性，将算法与运用径向基函数神经网络(RBF)雷达目标识别方法[13]进行了比较。仿真实验采用的数据为测量飞机数据，其脉冲重复频率为400 Hz，信号带宽为400 MHz，采用Dechirp接收，转换后信号的采样频率为10 MHz验数据飞机分别为, 大型喷气飞机“雅克Yark-42”、小型喷气飞机“奖状Jiang”和中小型螺旋桨飞机“安An-26”，为了更客观准确地验证识别方法准确性，训练和测试数据选取不同的数据段，其中每个HRRP样本含有256个距离单元，数据俯仰角有微小差别[14]。

实验基于目标中心散射模型[15]，主要用全局最小熵距离对齐算法对数据进行预处理，使用GRNN神经网络作为分类器，利用K重交叉验证法训练网络。将经过预处理后的数据随机抽取 12/13数据作为训练样本，剩下的则作为测试样本放入训练好的网络中进行训练计算目标识别准确率。

本实验使用Matlab将本文改进GRNN神经网络算法与传统RBF神经网络算法、GRNN神经网络算法进行对比，表1为3类飞机目标分别在3种算法下识别率。其中识别准确率的定义为正确识别样本个数/测试样本总数，识别率为仿真100次的平均识别率，每次的训练集和验证集均为随机选取。

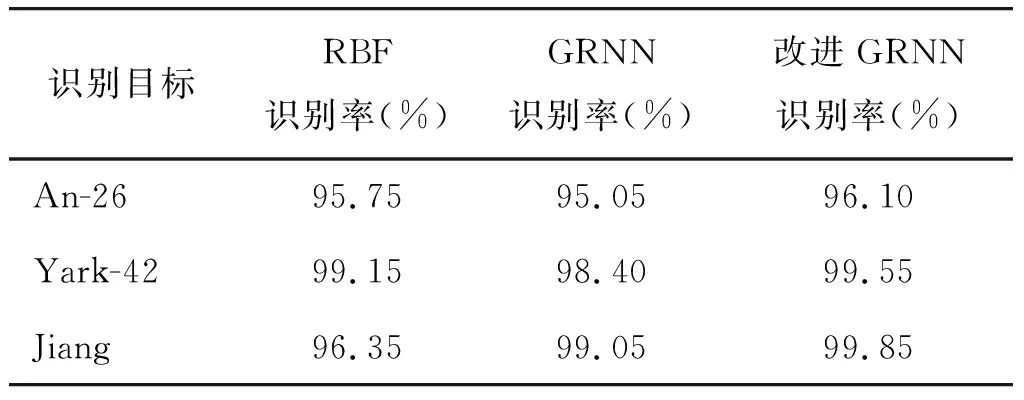
表1 针对不同飞机目标识别准确率Table 1 Target recognition accuracy for different aircrafts

仿真实验中网络光滑因子spread的最优值由最小均方误差(MSE)得出，图4所示为10-CV时不同Spread取值对神经网络MSE的影响。

由图4可以看出，在10次不同训练集和验证集情况下，虽然每次光滑因子spread最优位置即MSE的最低点位置都不同，但是大致位置基本在一定范围内，因此对图4的10重交叉验证后产生的10组数据进行累加，得出网络综合最优光滑因子spread的取值大小，如图5所示。

仿真主要从目标识别准确率和时间2个方面对应用了不同神经网络方法进行了比较，表2分别给出了采用不同神经网络时的识别准确率比较。从数据中可以看出，本文改进的GRNN神经网络算法与RBF网络以及原有GRNN网络算法相比具有相对较高的识别率。

表3对比了采用不同神经网络时的系统所用的运算时间，其中运算时间包括训练时间和测试时间。从表中可以看出，改进的GRNN神经网络算法运算时间明显少于RBF网络。

表2 几种算法对比的平均识别率Table 2 Average recognition rate of several algorithms

表3 几种算法对比的平均运算时间Table 3 Average computing time of several algorithms

4 结束语

本文对基于GRNN神经网络的雷达目标识别方法进行了研究，利用了全局最小熵距离对齐算法以及归一化等方法对数据进行了预处理，针对广义回归神经网络光滑因子spread参数采用K重交叉验证法对进行优化，并取得最优样本输入输出值。仿真实验结果表明，本文改进的GRNN神经网络解决了设计参数σ选取时的随意性，减少了人为因素对预测结果的影响，该方法模型的目标识别预测精度和稳定性上优于RBF神经网络模型，具有较高的识别率以及良好的识别效率。