大规模无人机遥感影像快速区域网平差
2018-08-22杜娟薛武赵蓓蕾
杜娟,薛武,赵蓓蕾
(航天工程大学,北京 101416)
0 引言
无人机(unmanned aerial vehicle,UAV)凭借机动灵活、性价比高的优势在航空遥感中发挥了重要作用,利用无人机影像进行目标定位成为遥感测绘与无人机应用领域的热点问题[1-4]。随着无人机遥感数据量越来越大,提高数据处理的效率成为不可回避的问题,特别是无人机影像的快速区域网平差是实现高精度对地定位的前提条件。因此,有必要研究无人机遥感影像的快速处理技术,为抢险救灾、军事行动等应急测绘保障提供技术支撑。
为了控制硬件成本,目前无人机遥感平台搭载的相机通常是消费级单反相机,其幅面一般从2 000万像素到5 000万像素,对于同样大小的测区,要想得到相同的立体覆盖的影像,所需要拍摄的影像数量是大面阵航测相机的数十倍。同样,受限于平台的载重能力,也为了降低成本,大多数无人机上没有搭载专业的POS(positioning and orientate system)设备,仅有用于平台本身姿态控制的导航级GPS(global positioning system)和INS(inertial navigation system)。因此不同于常规的载人遥感平台,无人机获取的数据无论是影像外方位元素还是加密点的数量均会增加很多。这就导致了区域网平差时待求参数的数量显著增多,对应误差方程和法方程的规模也明显增大。计算机处理时需要更多的RAM资源和更长的时间[5]。国内外学者针对光束法平差的收敛性、精度、鲁棒性等开展了诸多研究并取得了丰富的成果。但是,针对如何提高光束法平差的解算效率方面的研究相对偏少[4,6]。本文结合无人机遥感影像的特点,就如何提高无人机影像光束法平差的效率提出了一种解决方案。
为了解决无人机影像的“先天不足”,充分挖掘硬件平台的计算潜力,对大规模方程组的解算方法进行了改进,主要包括采用共轭梯度法迭代解算法方程,利用预条件矩阵减小法矩阵的条件数,计算矩阵的舒尔补减小计算量,并发挥计算机的计算优势对矩阵运算进行了并行化改进。
1 大规模无人机影像快速区域网平差
无人机搭载中小幅面数字传感器,其成像模型与传统航测面阵相机相同,即共线条件方程[7],如式(1)所示。
由于作业中各种误差的存在,式(1)并不严格成立,为了得到影像外方位元素和加密点的地面坐标的最大似然估计,将式(1)进行线性化,得到误差方程[8]:
vx=c11dXS+c12dYS+c13dZS+c14dφ+c15dω+
c16dκ+c17dX+c18dY+c19dZ-lx,
vy=c21dXS+c22dYS+c23dZS+c24dφ+c25dω+
c26dκ+c27dX+c28dY+c29dZ-ly.
(2)
光束法平差的目标是所有像方观测点的反投影误差平方和达到最小,其目标函数形式如下:
通常采用最小二乘方法对式(3)进行求解,式(2)的法方程如式(4)所示。求解法方程得到待求参数的最大似然估计,然后利用待求参数的更新值前方交会得到加密点地面坐标。
1.1 列文伯格-马夸尔特法
在实际的无人机遥感作业生产中,由于未知数的数量比较多,法方程系数矩阵具有奇异性,导致式(4)解算不稳定,本文采用参数估计中的列文伯格-马夸尔特(levenberg marquardt,L-M)方法克服法方程的奇异性。L-M方法能够自适应调整未知数的变化幅度,从而有效克服解的不稳定性,有些文献中也将其称为阻尼高斯牛顿法[9-10]。通过启发式方法,L-M在高斯牛顿法与梯度下降法之间自主转换,使得迭代运算快速收敛到全局极小值[1]。具体在无人机影像处理中,采用L-M方法后,能够在没有控制信息时自适应调整待求参数的变化幅度,克服法方程奇异带来的解的不稳定[11]。对式(4)应用L-M方法后,得到:
(5)
式中:λ1,λ2分别为对应于无人机影像外方位元素和加密点地面坐标的阻尼系数。
1.2 舒尔补矩阵简化法方程
无人机影像区域网平差时需要求解未知数较多,以n幅影像和m个加密点为例,待求参数的数量为6n+3m(6n个无人机影像外方位元素和3m个坐标)。尤其是为了得到更稠密的连接点,需要求解的地面点坐标往往超过百万级别,如此规模的方程组求解比较困难,直接解算会消耗大量的内存和计算时间,普通计算机也难以处理。
考虑到加密点坐标的数量远大于影像外方位元素的数量,因此借助Schur补方法将影像外方位元素和加密点坐标2类变量分开求解。在答解法方程时,首先解算无人机影像外方位元素,然后求解加密点坐标[12]。Schur补本质上是一种高斯消元法,通过分块的方式答解方程组,以下列方程组的答解为例:
未知数x,y的求解可以分为2步:利用高斯消元法,式(6)变换为如下形式:
得到未知数x的解后,带入式(6)求解未知数y,从而实现了2类变量的分离和分步求解,减少了未知数的数目。需要注意的是,对无人机影像处理而言,得到待求参数更新值之后可通过前方交会直接计算连接点三维坐标,无需回代到原来的方程进行计算,从而可以进一步减少计算量。
1.3 预条件共轭梯度法
处理大规模无人机数据时,式(7)是一个典型的大型稀疏矩阵,本文引入参数估计中的共轭梯度方法对其进行答解。如果按照求解方式划分,共轭梯度法是一种直接解法,但是运算中由于舍入误差的存在需要迭代求解,所以可以看作是正定方程组的迭代解法。共轭梯度法所需迭代次数与系数矩阵条件数是有关的,条件数越大需要的迭代次数越多。由于大规模无人机影像处理时未知数的数量多,而且系数矩阵的条件数比较大,因此在解算时会出现迭代次数多、收敛速度慢的情况。对此,本文采用预条件矩阵来降低式(7)的条件数[13],以下面的方程为例:
Ax=b.
(8)
为降低方程的条件数,等式两边各乘一个矩阵M-1可得:
M-1Ax=M-1b.
(9)
M-1的引入使得方程的条件数从A的条件数变为M-1A的条件数。如果M-1设计得当,可以大大降低式(8)的条件数,通常把矩阵M-1称为预条件矩阵。考虑到式(5)的雅克比矩阵是块状对角矩阵,容易构造和进行求逆运算,所以通常将其作为预条件矩阵。
1.4 截断牛顿法
预条件矩阵的引入能够在一定程度上减少共轭梯度法的迭代次数,如果处理海量数据、方程组规模非常大时,收敛速度依然比较慢。实际上,共轭梯度法在解算时,仅前面几次迭代对待求参数的修正量比较大,后面的迭代改正量较小。因此可以把消耗时间比较多、改正量不大的迭代运算舍去,仅保留前面几次改正量比较大的几次迭代。这样做还有一个重要原因就是在整个平差解算过程中,每次解算的结果均作为下一次迭代的初值,所以提前结束共轭梯度的迭代,用近似解代替严密解是可行的。
常用的共轭梯度法的近似解是截断牛顿法,顾名思义,截断牛顿法是牛顿法的一种改进方法,将迭代的终止条件从待求参数残差向量的阈值变为强制序列系数。强制序列系数的计算公式如(10),ηk表示第k次迭代的强制序列系数,c表示法方程常数向量,sk+1表示第k+1次迭代的残差向量。这样在进行法方程解算时,迭代的终止条件变为当前的强制序列系数小于阈值,从而有效减少了迭代次数,同时保持了迭代的收敛性。
1.5 CPU,GPU并行加速
当前消费级计算机都配置有多核CPU和GPU,可以充分发挥其计算潜力,在算法优化的基础上通过并行运算提高矩阵运算的效率。大规模无人机影像定位解算过程中消耗时间较多的步骤主要有:
(1) 像方残差计算;
(2) 稀疏矩阵计算;
(3) 预条件矩阵M构建;
(4) 矩阵相乘JcΔxc+JpΔxp;
(6) 矩阵相乘Mv。
以上运算中,(4)和(5)的时间开销最大,因为利用截断牛顿法迭代解算法方程时,每次迭代都进行一次运算,再考虑到定位解算整体迭代过程,其计算次数是十分可观的。而其他步骤虽然计算量也比较大,但仅在L-M的迭代求解时才运行一次,因此采用硬件对区域网平差过程进行加速的关键在于步骤(4)和步骤(5)。
从前文的介绍可以看出,无人机影像的定位解算过程需要频繁地读取和存储大型稀疏矩阵。如果按照传统数字摄影测量中的方式直接存储原始矩阵会消耗大量的内存空间,普通计算机难以满足需求,特别是大区域(上万幅)影像的处理将无法进行。为了解决这个问题,本文引入了一种更紧凑的矩阵存储形式——块压缩稀疏行(blocked compressed sparse row, BCSR)。BCSR本质上是压缩存储技术,其高度压缩、分块存储的特性能够大大减少对存储空间的需求[14]。BCSR利用4个向量
通过算法优化,区域网平差解算过程拆解为系列基础的矩阵计算,编程中结合使用SIMD (single instruction multiple data)和SSE(streaming SIMD extensions)以充分发挥当前计算机平台CPU和GPU的并行运算潜力[15-16],实现无人机影像的快速定位解算。
2 实验与分析
为对本文提出的大规模无人机影像区域网平差方案的效率进行验证,选择4组具有代表性的无人机影像进行实验,实验的软硬件环境如表1所示,实验数据情况如表2所示。为了体现本文加速方法的有效性,采用3种传统解决方案与本文方法进行对比实验,每种方案的技术流程如图2,3所示。具体来讲,方案1直接对Schur补矩阵进行Cholesky矩阵分解,方案2利用稀疏矩阵表示Schur补矩阵,方案3和方案4都采用本文方法对解算流程进行了算法优化,不同的是方案3在计算过程采用CPU多核并行进行了加速,方案4利用GPU并行对计算过程进行了加速。实验结束后,分别统计每种方法的时间消耗,结果见表3。
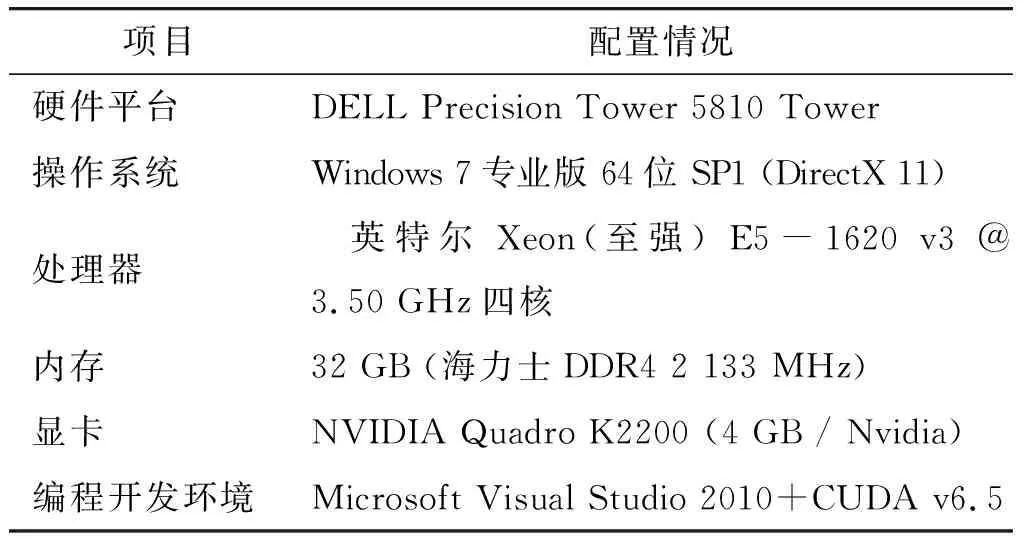
表1 实验软硬件环境Table 1 Experimental software and hardware environment

表2 实验数据情况Table 2 Experimental data situation
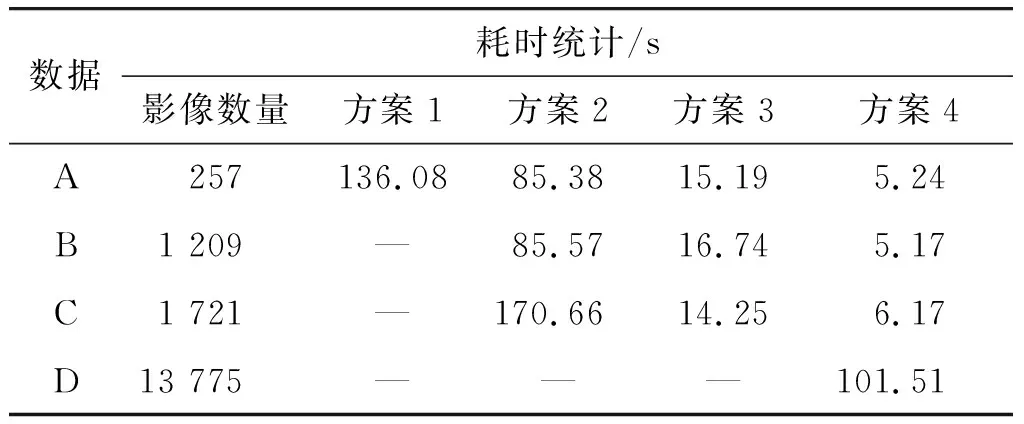
表3 时间消耗统计Table 3 Time consumption statistics
分析表3可以得出以下结论:
(1) 从不同方案的处理结果来看,方案1仅能处理几百幅量级的影像,方案2和方案3可以处理千余幅影像,而本文提出的方案4可以处理1万余幅影像。
(2) 从时间消耗来看,本文提出的方案计算效率很高,具有较高的加速比,能够快速处理大数据量无人机影像,具有重要的实用价值。
(3) 本文提出的解决方案在处理无人机影像时具有效率高、支持数量多的优势,对于无人机影像在应急测绘保障中的应用具有重要的实用价值。
3 结束语
无人机影像已经成为遥感探测的重要数据源,快速高效的无人机影像处理方案具有重要的研究价值和广阔的应用前景。本文为提高大规模无人机影像区域网平差的效率,分别从算法优化设计与硬件并行加速2个方面开展研究。算法优化方面采用矩阵的Schur补减少了未知数的数目,采用预处理矩阵减小了法矩阵的条件数,并利用共轭梯度的截断牛顿法答解法方程,同时利用块压缩稀疏行的紧凑方式存储稀疏矩阵,从而降低了对计算机内存和显存的开支。硬件加速方面分别采用CPU和GPU并行对矩阵运算进行了加速。通过几组有代表性的数据进行实验,证明了本文提出方法的有效性。下一步将针对无人机影像序贯平差开展研究,为无人机遥感数据的在线实时处理奠定技术基础。
