高超声速滑翔目标多层递阶轨迹预测

张凯，熊家军

(空军预警学院a.研究生管理大队；b.四系，湖北 武汉 430019)

0 引言

飞行器轨迹预测一直是态势与威胁评估、目标拦截的重大课题之一。高超声速滑翔目标(hypersonic gliding reentry vehicle, HGRV)作为新一代跨大气层空天飞行器，结合了航天器与航空器的特征，具有高空、高速、机动性强、跨度大等特点[1-2]，传统弹道目标预测方法难以对其轨迹准确预测。针对HGRV这类非惯性目标的轨迹预测问题，必须结合目标特点寻求新的思路。

轨迹预测的关键在于估计目标状态与构建预测模型，而这2类问题往往都是基于目标建模展开的[3]。当模型不能够准确反映目标运动特征时，会造成较大的预测误差。传统的CV (constant velocity)，CA (constant acceleration)，CT (coordinate turn)以及Singer等统计模型无需任何目标的先验信息，但也限制了预测模型精度[4-6]。受气动力影响，HGRV再入时往往受到特定环境、技术因素影响，具有显著的动力学特性，且在某些方面呈现出确定性特征。根据这些特征对目标进行动力学建模，可有效提高模型精度。此类方法一般根据观测数据辨识出目标的制导规律[7]、速度倾角[8]、升阻比[9]等参数，结合预测初始状态外推实现轨迹预测。作为非合作目标，防御方往往对HGRV缺乏深入认知，构建的模型难以描述目标真实运动状态。因此，模型误差是客观存在的，且不可避免。如果不对模型误差进行补偿，那么即使观测数据没有任何误差，轨迹预测的偏差也会相当“可观”。可见，面对量测和模型误差等问题时，在建模基础上对模型误差进行补偿是提高HGRV轨迹预测精度的有效途径。

为此，本文借鉴利用多层递阶理论将轨迹预测过程分离成2个部分：一部分是对时变的气动参数和模型误差进行预测，通过在动力学模型上加入附加噪声表示模型误差，将附加噪声与气动参数进行混合估计，实现模型随机补偿；另一部分是以参数预测值为基础，利用参数预测值的变化表征目标未来的制导规律进行轨迹预测。期望通过这种多层递阶预测思想为高超声速滑翔目标轨迹预测等提供一定理论指导。

1 多层递阶模型补偿

预测模型参数补偿实质上是系统辨识问题，对于这类满足某些基本规律、但又有些待定因素的建模问题，在系统辨识中称为“灰箱”问题。这就要求理论建模与数据建模相结合，对机理已知部分采用动力学建模；对机理不清楚部分采用数据建模，利用量测数据辨识出动力学模型的未知参数。

1.1 随机补偿原理

假设目标真实动力学模型为

X(k+1)=f(X,u,k),

(1)

式中：u表示时变参数向量。已知简化的线性动力学模型为

X(k+1)=F(k)X(k)+G(k)u(k)+(k).

(3)

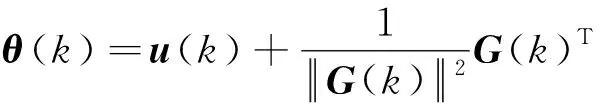
(4)

即有

X(k+1)=F(k)X(k)+G(k)θ(k).

(5)

1.2 多层递阶预测

多层递阶预测理论[11]一般将预测问题分成2部分，即预测模型时变参数的预测和在此基础上得出的对预测对象的预测。一般认为状态d步预测值可通过对式(5)积分获取：

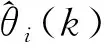
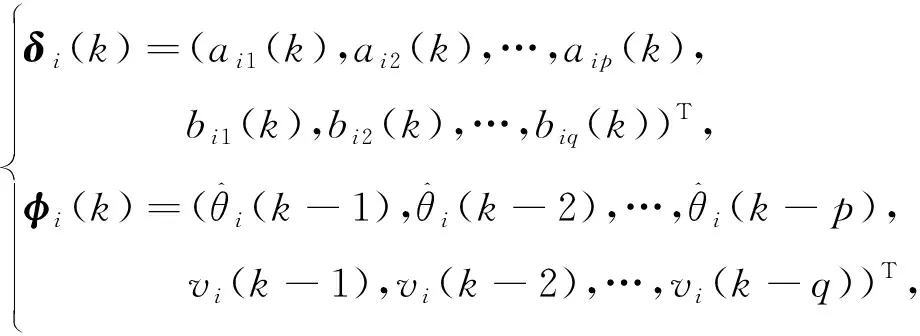
(9)

则有

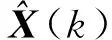
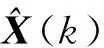
2 轨迹预测算法

2.1 动力学建模

对于HGRV这类机动再入目标的动力学建模问题，比较流行的做法是将气动参数作为未知机动输入增广到状态向量之中，构建扩展的动力学模型[13]。为此，首先应对气动加速度a进行分析。在半速度(velocity-turn-climb，VTC)坐标系中用矢量形式描述HGRV的气动加速度a的表达式为

a=-Duv+L(-utsinφ+uccosφ),

(12)

式中：

(13)

式中：uv，ut和uc分别为VTC坐标系中各坐标轴方向单位矢量；CD，CL分别为阻力系数和升力系数；φ为滚转角，是HGRV主要的控制参数；D为阻力加速度，L为升力加速度；S为目标等效截面积；m为目标质量；v为目标速度；ρ为大气密度。

在式(12)中，气动加速度a由3项组成：① 沿速度方向的阻力加速度D； ② 水平转弯方向的Lsinφ； ③ 爬升方向的Lcosφ。对于非合作目标而言，目标控制参数α和φ，以及CD,S和m等均为未知参数。为了减小参数估计的困难，可定义气动参数u间接表征目标的控制规律：

(14)

式中：αv，αt和αc分别为阻力参数、转弯力参数和爬升力参数。参照文献[14]在东北天(East-North-up，ENU)坐标系中建立气动加速度a与气动参数u的关系式：

(16)

式中：r为目标瞬时地心距；B为雷达站地理纬度；Re为地球半径。

2.2 未知参数混合估计

状态估计主要包括系统模型和量测模型。气动参数u为系统模型的未知量，附加噪声为系统模型与真实模型的偏差，根据上文模型补偿的论述，应对θ=u+进行混合估计。这里采用一种简单的做法：将附加噪声作为气动参数的噪声，即直接估计气动参数u。由于考虑了模型噪声，对气动参数进行估计时不能采用传统白噪声的统计特性，可采用一阶马尔科夫模型表示其统计特性：

(17)

式中：λv,λt和λc分别为对应气动参数的机动频率；wv,wt和wc分别为对应的零均值高斯白噪声。至此，面向状态估计的目标系统模型可表述为：对状态方程(17)进行离散化，且令未知参数θ=(αv,αt,αc)T，联立式(16)和(17)，即可得到离散形式的动力学模型式(5)。

3 轨迹预测流程

本文所提轨迹预测的基本思想可表述为：根据混合估计的历史气动参数数据训练时间序列预测模型，得到参数预测值。然后，基于参数预测值利用动力学模型(5)积分实现轨迹预测。具体流程为：

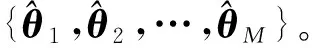
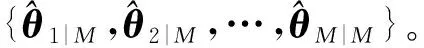
4 算法仿真与分析

仿真实例模型参考美国洛马公司的CAV-H的基本参数[16]。假定相控阵雷达采样间隔为0.1 s，距离量测标准差为500 m，角量测标准差为0.01 rad，选取跟踪滤波时间为120 s，轨迹预报时间为400 s，采用ARIMA模型对进行参数拟合和预测。假设以下仿真场景：飞行模式1为纵向跳跃飞行，目标滚转角始终为0，攻角为随速度线性变化的函数；飞行模式2横向转弯飞行，目标滚转角始终保持20°，攻角为随速度线性变化的函数。

4.1 纵向跳跃飞行仿真

图1给出了飞行模式1下气动参数跟踪与预测结果。可以看出，在目标始终保持0滚转角的飞行条件下，气动参数真实值呈近似直线变化。此时算法可以较好地跟踪气动参数，根据估计值训练ARIMA模型对气动参数的预测可以较好地逼近真实值，400 s内最大预测偏差分别为7%，4%和9%。

图2和图3分别给出了飞行模式1下目标轨迹的跟踪与预测结果以及跟踪时间与位置偏差的关系。从图2不难看出，轨迹跟踪值和预测值都能够较好地逼近真实轨迹，随着预测时间的增加，预测误差逐渐增大，但总体处于在0～5 km量级，预测误差在允许范围内。从图3中看出，跟踪时间较短时，预测偏差随时间呈指数增长，方法鲁棒性较差；跟踪时间较长时；随着跟踪时间的增加，时间序列模型可以通过量测数据获得更多关于目标控制规律的先验信息，预测偏差随时间呈线性增长，对气动参数预测精度有所提高。

4.2 横向转弯飞行仿真

图4给出了飞行模式2下气动参数跟踪与预测结果。可以看出，在目标始终保持20°滚转角的飞行条件下，气动参数真实值呈近似二次曲线变化，此时预测偏差随时间逐渐增大，400 s内最大偏差分别达到15%，9%和18%。同时，对比2种飞行模式，当目标发生横向机动，气动参数的预测性能会变差。

图5和图6分别给出了飞行模式2下目标轨迹的跟踪与预测结果以及跟踪时间与位置偏差关系。从图5不难看出，对于横向转弯飞行而言，虽然气动参数预测偏差会增大，但预测值仍然能较好地反映目标的运动趋势。从图6中可以得到类似飞行模式1中的结论，但不同的是，飞行模式2中轨迹预测误差总体处于在1～10 km量级。这是由于当目标发生横向机动时，时间序列模型难以准确预知气动参数的变化，从而导致方法预测误差显著增大。

5 结束语

本文研究了一种基于模型误差补偿的HGRV分层递阶轨迹预测方法。将HGRV轨迹预测问题分解为气动参数与模型误差的混合预测和在此基础上对飞行轨迹的预测，论述了方法流程及其合理性。

在假设HGRV按照一定规律飞行情况下设置2种飞行模式的仿真场景，分析了跟踪和预测时间等因素对预测精度的影响。仿真结果表明，所提方法具有稳定可靠的轨迹预测能力，但横向机动会造成方法误差增大。针对HGRV机动等不确定因素对轨迹预测问题带来的困难，课题下一步的研究方向是结合目标的当前状态和飞行意图，探索目标机动不确定条件下的轨迹预测方法。