延性节点钢框架结构的抗震性能分析
2018-08-21韩明岚
韩明岚,王 帅,牟 政,王 燕,刘 丹
(1. 青岛理工大学 蓝色经济区工程建设与安全协同创新中心,山东 青岛 266033; 2. 山东科技大学 土木工程与建筑学院,山东 青岛 266590; 3. 青岛理工大学 土木工程学院,山东 青岛 266033; 4. 鲁东大学 土木工程学院,山东 烟台 264025)
0引 言
钢结构强度高、延性好,具有良好的抗震性能,被广泛应用到多层和高层建筑中。结构水平位移随建筑高度增加而增大,为减小结构在水平荷载作用下的侧移,梁柱节点通常采用全焊接或栓焊连接,形成全刚性节点[1]。在20世纪末美国北岭地震与日本阪神地震中,传统的刚性节点发生了不同程度的脆性断裂现象[2-4],这促使工程界学者开始深入研究梁柱连接的受力性能及破坏机理,对钢框架梁柱节点抗震性能不断进行优化,设计并提出了两大类抗震性能良好的新型延性耗能节点[5-9],分别为加强型节点和削弱型节点。
对比普通节点,延性耗能节点构造较为复杂,尽管精细化有限元能够很好地完成高层或超高层延性节点钢框架结构动力计算,但比较繁琐,为节省计算时间,降低计算成本,有必要对延性节点框架结构进行合理简化,对简化后的结构模型进行数值计算,以期在节省资源的同时,得到较为准确的计算结果。
本文共设计了2个6层三跨和2个12层两跨的翼缘圆弧式削弱型节点(Reduced Beam Section Connection,RBS节点)框架和盖板加强型节点(Cover-Plate Reinforced Connection,CPR节点)框架,利用延性耗能节点简化模型对框架进行简化,对简化后的框架模型进行模态分析和动力时程分析,提取框架基本周期、框架柱顶位移和柱底剪力时程曲线,将计算结果和实际模型的计算结果进行对比,2种模型的计算结果吻合较好,说明利用延性耗能节点框架简化模型进行动力计算可有效分析框架结构的抗震性能。
1节点简化模型
普通节点简化模型研究历史较长且相对成熟,最早有学者提出一种三弹簧节点简化理论模型[10],见图1。施刚等[11]采用普通节点简化模型,并结合节点转角测量方法进行了框架静力分析,获得了较为精确的计算结果。

图1普通节点简化模型Fig.1Simplified Models of Ordinary Connection
对比普通节点,延性节点的最大特点是强震下塑性铰远离梁柱连接区域,因此延性节点简化模型要充分考虑塑性铰形成的位置。文献[12]提出了图2所示3种延性节点简化模型,相比图1(a)所示的普通节点简化模型,图2(a)所示的延性节点简化模型转动弹簧布置在塑性铰处,以模拟两侧连接组件的变形;图2(b)所示的模型中节点域采用转动弹簧来替代图2(a)中的斜拉弹簧,体现节点域剪切变形;图2(c)中的节点域设置为刚性,不考虑节点域剪切变形。
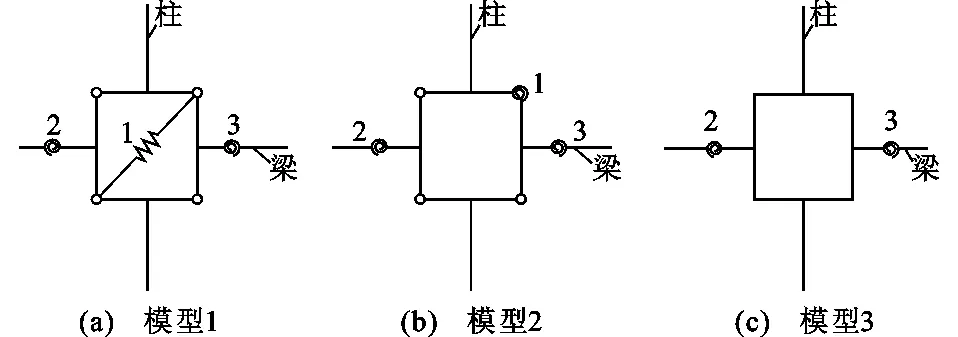
图2延性节点简化模型Fig.2Simplified Models of Ductile Connection
2框架和节点模型
2.1框架模型
根据抗震规范[13],分别设计6层和12层平面钢框架,框架节点形式为RBS节点与CPR节点,框架结构立面图见图3,框架梁、柱均为H型截面,选用Q345钢材,弹性模量为206 GPa,泊松比为0.3,材料弹塑性模型选用多线性等效强化MISO模型,应力-应变(σ-ε)曲线见图4,框架梁、柱几何尺寸见表1。
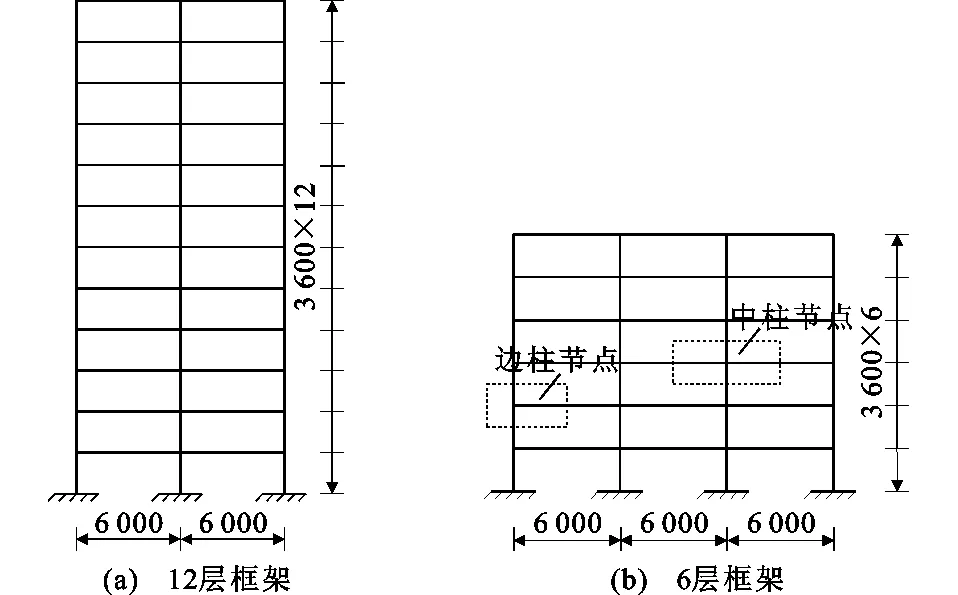
图3框架结构立面图(单位:mm)Fig.3Elevations of Frame Structures (Unit:mm)
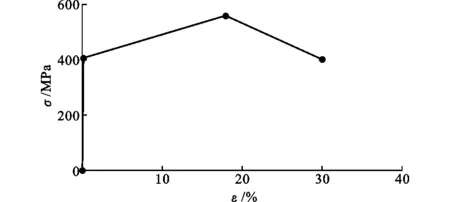
图4应力-应变曲线Fig.4Stress-strain Curve

构件名称截面尺寸长度/mm12层梁500 mm×250 mm×12 mm×16 mm6 00012层柱500 mm×500 mm×20 mm×24 mm3 6006层梁400 mm×180 mm×10 mm×14 mm6 0006层柱400 mm×300 mm×12 mm×18 mm3 600
2.2节点模型
图3所示框架结构中的节点分别为RBS节点与CPR节点,节点具体构造见图5,其中a为削弱起点至柱面距离,b为削弱长度,c为削弱深度,bf为梁翼缘宽度,hb为梁高度,l为盖板长度,t为盖板厚度,b1为梁上盖板宽度,hc为柱高度。
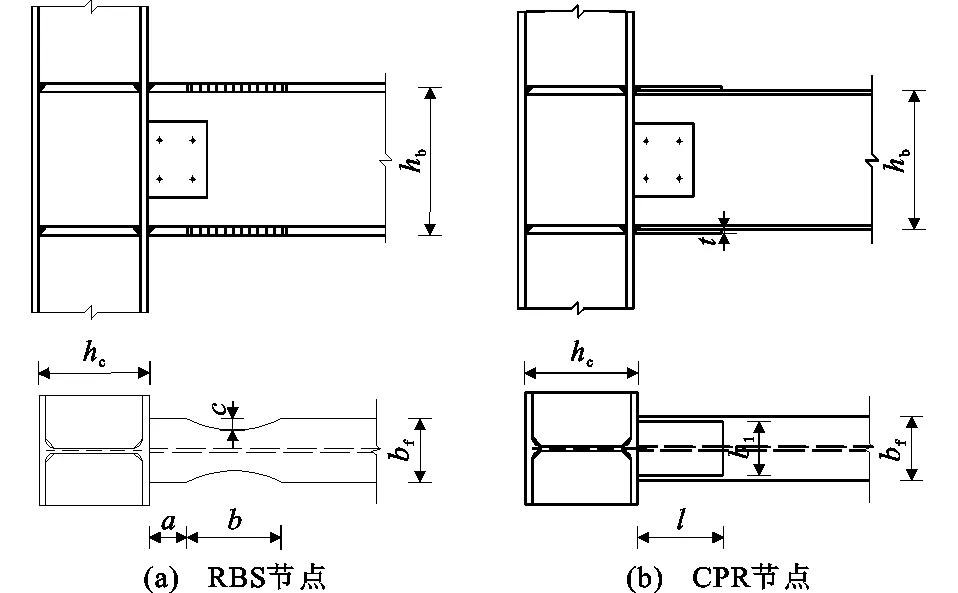
图5延性节点构造Fig.5Construction of Ductile Connections
根据文献[14],[15],RBS节点削弱处尺寸取值范围为
a=(0.5~0.75)bf,b=(0.65-0.85)hb,
c=(0.20~0.25)bf
根据文献[16],CPR节点盖板尺寸取值范围为
0.5hb≤l≤0.83hb,0.73tb≤t≤1.63tb,
b1=bf-2tb,b2=bf+2tb
式中:b2为梁下盖板宽度;tb为梁翼缘厚度。
依据上述取值范围并满足规范设计,各框架节点削弱处及盖板加强处几何参数见表2,3。

表2削弱处几何尺寸Tab.2Geometrical Dimensions of Reduced Section

表3盖板几何尺寸Tab.3Geometrical Dimensions of Cover-plate
3节点模型刚度设置
由于框架简化计算模型主要来源于延性节点的简化,因此首先要利用有限元对框架中的节点实体模型进行拟静力分析,提取节点简化模型中相应弹簧单元的刚度,再将弹簧单元刚度代入到框架简化模型中,从而得到一个符合实际受力特征的框架简化模型。本文选用图2(a)所示的节点简化模型,合理设置节点域斜拉弹簧和梁两侧弹簧的刚度是保证框架计算精度的关键因素。
3.1节点模型数值研究
以6层三跨框架为例,从梁、柱中点处对框架进行划分,把框架分成多个边柱节点单元和中柱节点单元,见图3。对图3所示RBS节点6层框架和CPR节点6层框架的边柱节点和中柱节点实体模型进行数值计算,采用Solid92实体单元划分网格,对节点域处、盖板加强处和削弱处网格加密,梁端节点垂直于梁轴线方向位移耦合,平面外位移约束,上下柱脚为铰接,通过位移控制在梁端施加低周往复荷载[17],计算后提取节点的滞回曲线和骨架曲线,分析边柱节点和中柱节点的本构关系,进而确定弹簧单元的荷载-变形曲线。6层框架中柱节点有限元模型见图6。

图66层框架中柱节点有限元模型Fig.6Finite Element Models of Mid-column Connections in 6-layer Frame
3.2节点域弹簧刚度
在侧向力作用下,忽略其他因素的影响,节点域以剪切变形为主,受力分析图7(a),等效剪力分析见图7(b),其中M1,M2为梁端弯矩,V1,V2为梁端剪力,M3,M4为柱端弯矩,V3,V4为柱端剪力,VA,VB分别为梁端等效剪力和柱端等效剪力,hcw,hbw分别为柱腹板高度和梁腹板高度。

图7节点域受力分析Fig.7Force Analysis of Panel Zone
等效剪力计算公式为[12]
VA=(M1+M2)/hbw-(V3+V4)/2
(1)
VB=(M3+M4)/hcw-(V1+V2)/2
(2)
图2(a)中轴向拉压弹簧刚度由节点域拉压弹簧力F和对角线伸缩量δ对应的关系给出,其表达式分别为[18-20]
γ=Mγ/(Ghcwhbwtp),Mγ=VAhcw=VBhbw
式中:γ为剪切角;Mγ为剪切力矩;tp为节点域厚度;G为剪切弹性模量。
3.3梁两侧弹簧刚度
普通节点简化模型中,梁两侧转动弹簧刚度可直接由节点处弯矩-转角关系确定,但对于延性节点简化模型,梁两侧弹簧单元设置在塑性铰处,弹簧刚度需要根据塑性铰处的弯矩-转角关系确定。
在节点实体模型有限元分析中采集节点转角,节点转角定义为荷载作用下梁柱夹角相对于无荷载时的改变值,在图8中位置1~4处分别提取位移,位置1,2处竖向位移分别用Δ1,Δ2表示,位置3,4处水平位移分别用Δ3,Δ4表示,节点转角θ的计算公式为[11]
θ=(Δ3-Δ4)/hbf-(Δ1-Δ2)/hcf
(3)
式中:hbf为梁上下翼缘中心线的距离;hcf为柱上下翼缘中心线的距离。

图8节点转角测量方法Fig.8Measuring Method of Connection Rotation
根据节点弹性转角和塑性转角导出塑铰处转角θ′为[12]
(4)
式中:θe为塑性铰处弹性转角;θp为塑性铰处塑性转角;e为塑性铰与柱翼缘的距离。
节点弯矩分布见图9,梁端弯矩Mc和塑性铰处弯矩Mp的对应关系为
(5)
梁两侧弹簧刚度由Mp-θ′关系确定,基于第3.1节中计算得到的节点滞回曲线和骨架曲线,根据公式(4),(5)计算塑性铰处转角和弯矩,其对应的弯矩-转角关系曲线见图10。

图9节点弯矩图Fig.9Bending Moment Diagram of Connection
4模态分析
模态分析是结构动力分析的基础,通过模态分析可确定结构的振动特性,包括基本周期和各阶振型。将6层框架采用Beam188单元建立数值分析实际模型,为便于后续说明,RBS节点框架与CPR节点框架实际模型编号分别为6rbf-1和6cpf-1,同时将6层框架利用图2(a)所示的节点简化模型进行简化,简化模型中梁、柱采用Beam188单元划分,节点域斜拉弹簧与梁两侧弹簧均采用Combin39单元模拟,框架简化模型编号分别为6rbf-2和6cpf-2;12层框架进行同样的数值建模,实际模型编号分别为12rbf-1和12cpf-1,简化模型编号分别为12rbf-2和12cpf-2。对框架模型进行模态分析,提取前3阶基本周期T1~T3进行对比,6层与12层框架模型的基本周期见表4,5。
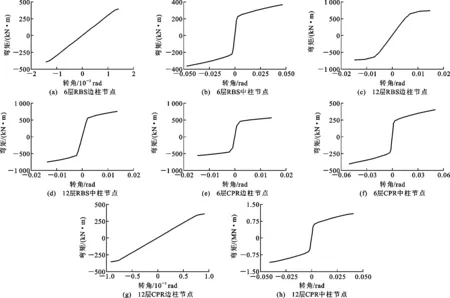
图10塑性铰处弯矩-转角骨架曲线Fig.10Moment-rotation Skeleton Curves in Plastic Hinge Location
从表4,5可以看出:框架简化模型计算得到的基本周期和实际模型计算值基本一致,其中RBS节点框架实际模型计算得到的前3阶基本周期比RBS节点框架简化模型的计算值稍大,两者相对误差在8.5%以内;CPR节点框架实际模型计算得到的基本周期比简化模型计算值稍小,两者相对误差在4%内。可见采用简化模型进行模态分析具有一定的可靠性。
5动力时程分析
场地为Ⅱ类场地,抗震设防烈度为8度,在罕遇地震下选取El Centro波与Taft波对框架进行弹塑性时程分析,将地震波加速度峰值均调整为400 cm·s-2。以6层RBS节点框架为例,框架有限元模型见图11。

表46层框架基本周期Tab.4Fundamental Periods of 6-layer Frame
注:T6r1,T6r2,T6c1,T6c2分别为框架模型6rbf-1,6rbf-2,6cpf-1,6cpf-2计算得到的基本周期。
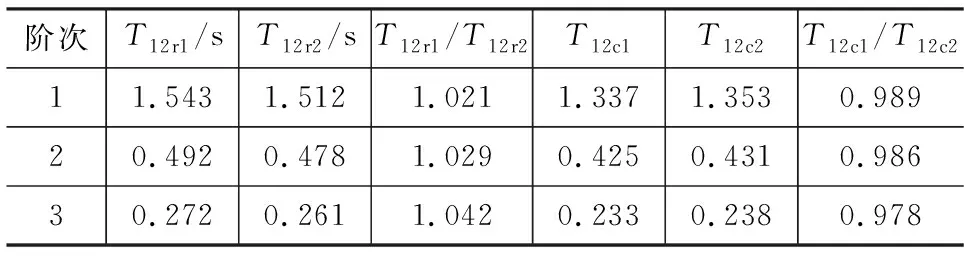
表512层框架基本周期Tab.5Fundamental Periods of 12-layer Frame
注:T12r1,T12r2,T12c1,T12c2分别为框架模型12rbf-1,12rbf-2,12cpf-1,12cpf-2计算得到的基本周期。
5.1El Centro波下弹塑性时程分析
El Centro波下对6层和12层框架实际模型和简化模型分别进行动力时程分析,将计算结果进行对比,框架柱顶水平位移时程曲线和柱底剪力时程曲线对比见图12,13。
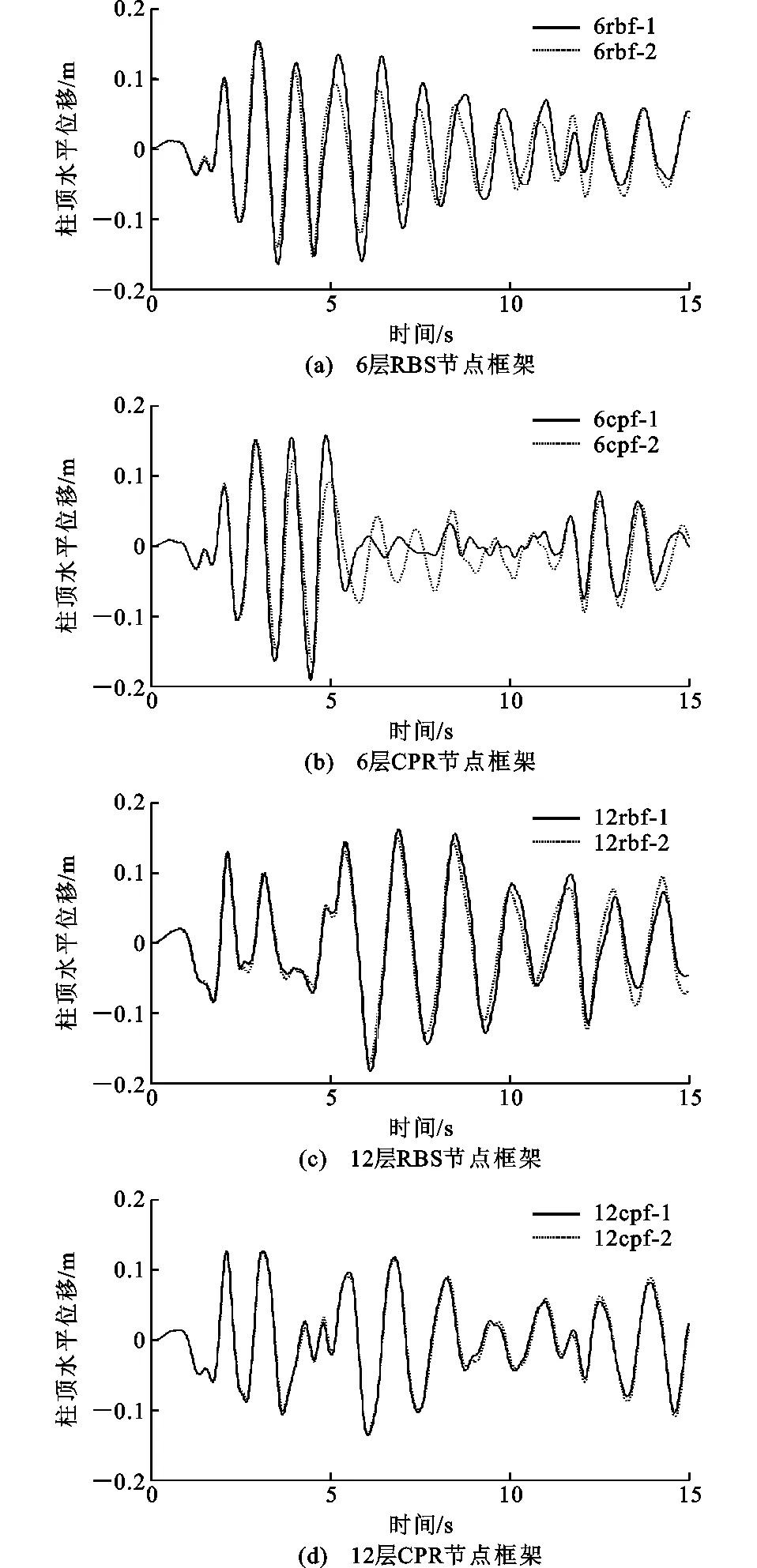
图12El Centro波下柱顶水平位移时程曲线Fig.12Horizontal Displacement Time-history Curves of Top Column Under El Centro Wave

图13El Centro波下柱底剪力时程曲线Fig.13Shearing Force Time-history Curves of Column Bottom Under El Centro Wave
从图12,13可以看出:2种框架模型计算得到的时程曲线变化规律基本一致,曲线幅值比较接近;模型12cpf-1和模型12cpf-2计算结果吻合最好,模型6rbf-1计算得到的时程曲线均滞后于模型6rbf-2计算得到的时程曲线,这是由于在El Centro波有效时间内,模型6rbf-1自振频率小于模型6rbf-2所致。
为进一步对比节点简化模型对框架动力计算的影响,以及削弱型节点和加强型节点对框架抗震性能的影响,提取El Centro波下6层框架和12层框架的柱顶位移极值和柱底剪力极值进行分析,如表6所示。
从表6可以看出:实际框架模型计算得到的柱顶位移与柱底剪力均比简化框架模型计算值略大,其中模型6cpf-1计算得到的柱顶位移极值比模型6cpf-2计算值大2.18 cm,比柱底剪力极值大26.13 kN,约增加13.8%;12层CPR节点框架比同尺寸RBS节点框架柱顶位移小且柱底剪力大,说明在强震下CPR节点框架抗震性能优于RBS节点框架。
5.2Taft波下弹塑性时程分析
Taft波下对所有框架模型进行动力时程分析,将计算结果进行对比,框架柱顶水平位移时程曲线和柱底剪力时程曲线对比见图14,15。
由图14,15可知:在Taft波作用下的大部分时间内,实际模型与简化模型计算得到的时程曲线变化规律基本一致;在经历地震波加速度峰值后的8~11 s时间段内,模型6rbf-1和模型6rbf-2计算得到的曲线差值较为明显。
提取Taft波下6层框架和12层框架的柱顶位移极值和柱底剪力极值进行分析,见表7。从表7可以看出:实际模型计算得到的柱顶位移与柱底剪力比简化框架模型计算值略大,其中模型12rbf-1和12rbf-2计算得到的柱顶位移极值和柱底剪力极值差别略大,其中位移相差3.95 cm,剪力相差57.69 kN;CPR节点模型比同尺寸RBS节点模型柱顶位移小且柱底剪力大,表现出更好的抗震性能。
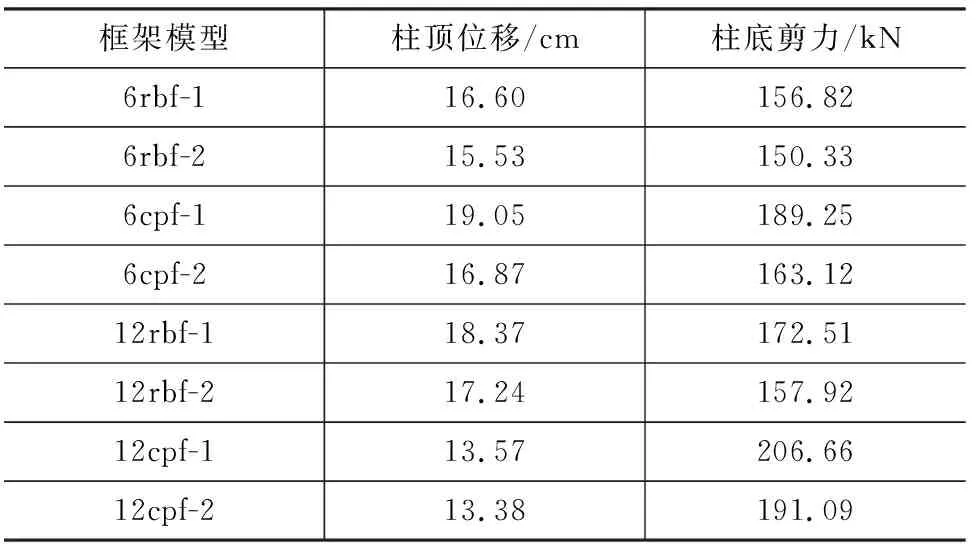
表6El Centro波下框架位移和剪力极值Tab.6Extreme Displacement and Shear Force of Frame Under El Centro Wave
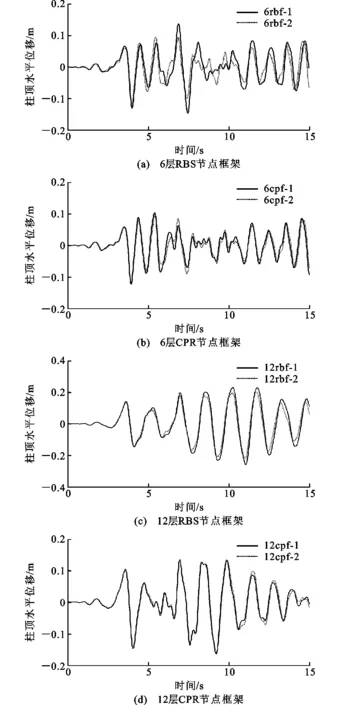
图14Taft波下柱顶水平位移时程曲线Fig.14Horizontal Displacement Time-history Curves of Top Column Under Taft Wave
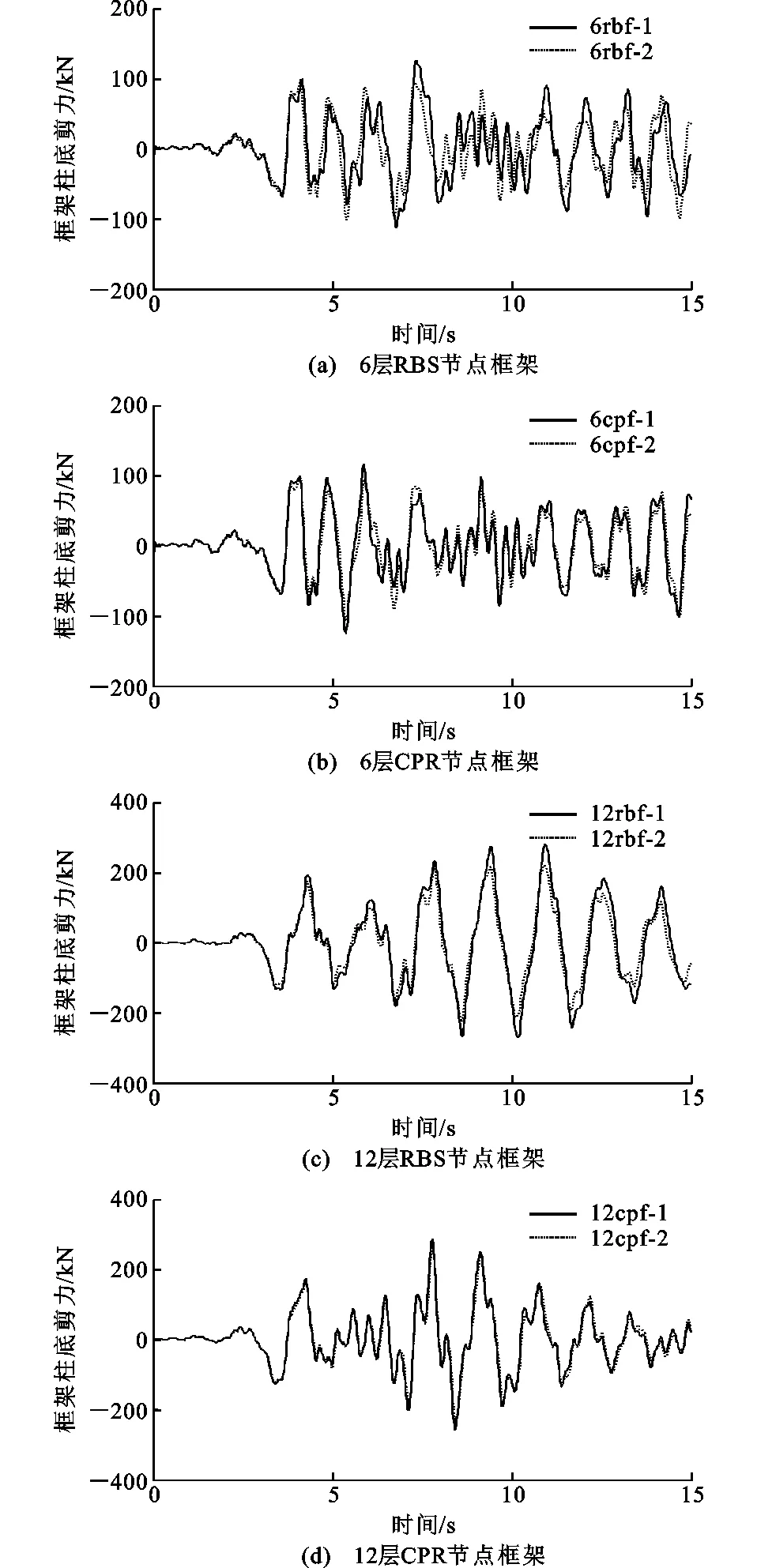
图15Taft波下柱底剪力时程曲线Fig.15Shearing Force Time-history Curves of Column Bottom Under Taft Wave

表7Taft波下框架位移和剪力极值Tab.7Extreme Displacement and Shear Force of Frame Under Taft Wave
6结语
(1)利用延性耗能节点简化模型对框架结构进行动力计算,框架的柱顶水平位移时程曲线和柱底剪力时程曲线的计算结果与实际框架模型的计算结果吻合良好,利用简化模型可在保证计算精度的前提下大幅提高计算效率。
(2)由于延性耗能节点充分考虑了节点域变形、节点组件变形以及塑性铰的位置等因素,能够较好模拟节点的力学特性,通过分析节点实体模型,提取合理的刚度赋予弹簧单元,使得节点简化模型与实际结构中节点的受力对应,因此在框架简化模型数值计算中能够得到较为准确的计算结果。
(3)简化模型的延性耗能节点可以取代较为复杂的削弱型或加强型实体节点,将复杂实体结构简化为简单模型进行数值计算,为框架结构的抗震性能分析提供可靠的方法。
