Observer-based control for the platform of a tethered space robot

Gung ZHAI,Heming ZHENG ,Bo ZHANG

a Aerospace Engineering School,Beijing Institute of Technology.Beijing 100081,China

b Aerospace System Engineering Shanghai,Shanghai 201109,China

KEYWORDS

Abstract This paper addresses the attitude control problem of a space tethered robot platform in the presence of unknown external disturbance caused by a connecting elastic tether.The tether generated unknown disturbance leads to tremendous challenges for attitude control of the platform.In this work,the perturbed attitude dynamics of the platform are derived with a consideration of the libration of the elastic tether,and then with the purpose of compensating the unknown disturbance,major attention is dedicated to develop a nonlinear disturbance observer based on gyros measurements,after which,an adaptive attitude scheme is proposed by combining the disturbance observer with a sliding mode controller.Finally,benefits from the observer based on an adaptive controller are validated by series of numerical simulations.

1.Introduction

Recently,the fast increment of debris in Earth’s orbit has received significant attentions.Evaluation on the orbital environment indicates that large space debris,such as nonfunctional satellites and upper stages,are ensured to impose the most serious impact to the orbit environment in the near future.With the purpose of suppressing the rapid growth of the debris population,different types of space robot systems are proposed for debris capture and removal.Lots of previous work in this field is focused on space robots with manipulators,1–5while other researchers6,7have proposed tethered space robots(TSRs)for large-size debris capture and removal.A TSR system is commonly composed of a maneuverable platform and a tether-connected net/gripper.Compared with a manipulator-based space robot system,a TSR achieves potential advantages due to its enhanced error tolerance,increasing capturing distance,and reliable safety.

There are many challenges arise from TSR practical implementation,one of which is the control problem for the post-capture system.Generally,the dynamic behaviors of a post-capture TSR are very similar to those of a typical tethered satellite system.Tethered satellites have been extensively studied in the past decades under the mass point and inelastic tether assumption.The dumbbell model is widely used to describe the tether libration within a local vertical local horizontal frame.For example,based on the dumbbell model,Williams8investigated the dynamics and control problem for a tethered system in an elliptical orbit,and his work indicates that certain combinations of parameters may lead to a tether slack.Motivated by the potential application for orbital transportation,Lorenzini9studied the problem of target rendezvous with a tether tip.To facilitate the relative motion analysis between the tether tip and a target,Takeichi et al.10extended his work to find a periodic solution of the tether librational motion in an elliptic orbit.Wen et al.11–13also studied the deployment and retrieval control problem based on tether tension regulation.Liu et al.14also extended the previous work to a tether satellite in a halo orbit,and a nonlinear output tracking control scheme based on the θ-D technique was proposed for system station-keeping control.

Due to the weakness of the dumbbell model,many researchers have tried to develop the detailed dynamics of a TSR by taking into account the tether elasticity.However,under the tether elasticity consideration,the longitudinal vibration of high frequency on a connecting tether makes the control problem even more challenging.With the efforts to guarantee TSR safeties,many researchers have dedicated their work to control techniques for the post-capture system.In order to avoid possible collisions between captured debris and the platform,Okazaki and Ohtsuka15developed a switching control scheme,and the safety insurance conditions for the post-capture TSR were analytically derived; finally,a satisfactory performance of the safety control scheme was validated by numerical simulations.By using Lagrangian theorem,Aslanov and Yudintsev16studied the dynamics of a post-capture TSR before a space tug,in which the influences from debris initial conditions and dynamic parameters,such as debris tumbling,tether elasticity,and thruster accelerations,were investigated and numerically demonstrated.With considerations of system uncertainties,Cleary and William17developed a wave-based control method to cope with the post-capture system,and this control scheme is easy to implement in practice due to its less relative measurement requirement.Huang et al.18–20presented a robust adaptive back-stepping controller to stabilize a tether-connected debris-gripper combination,and based on utilization of the auxiliary design and the optimal control scheme,the proposed controller effectively reduced possibilities of thruster saturation.

As well as guaranteeing system safety,platform attitude stabilization is also an important aspect for the post-capture system.In particular,the post-capture TSR is required to perform orbital maneuvers for debris removal.However,during the maneuvers,since attitude misalignment evidently leads to a remarkable increment on fuel consumptions,the attitude of the platform should be stabilized precisely with respect to the given reference.However,the tether-generated disturbance,which includes both long-term libration and elastic vibration,greatly increases the difficulties of platform stabilization.In the early 1990s,optimal control based on an integral linear quadratic regulator21(LQR)was proposed to suppress the resonances on flexible spacecraft,but LQR applications are very limited due to its dependency on accurate dynamic models.To cope with unknown external disturbances,robust attitude control techniques have attracted much attention in recent years.One of the robust attitude control methodologies is the observer-based control technique,which estimates external unknown disturbances based on necessary measurements for feed forward compensation.By incorporating a disturbance observer into the control loop,Yan and Wu22proposed a robust composited attitude control scheme for flexible spacecraft stabilization.Lee23addressed the problem of relative attitude control between two spacecraft subjected to an unknown disturbance,and a disturbance observer was also used to enhance the control performance.Liu et al.24also proposed a composite controller by combining a disturbance observer with a PD controller for attitude stabilization and vibration reduction of flexible spacecraft,and similar contributions are also available in the literature.25,26However,in the above mentioned works,an unknown disturbance is supposed to be slow time-varying,and sometimes approximately treated as a constant;therefore,for the case of disturbance with components of high frequency,perhaps the control performance will be greatly degraded.

In this paper,in order to enhance the attitude stabilization performance for a post-capture TSR platform,an adaptive controller is developed by combining a disturbance observer with a sliding mode controller to reject a disturbance from the elastic tether libration.Major attentions are dedicated to develop a nonlinear disturbance observer which only depends on gyros measurements.In comparison with the works in literature23,24,the proposed disturbance observer in this paper also works robustly in case of arbitrary time-varying disturbance,and meanwhile,the sliding mode controller in the control loop accounts for the residual disturbance after feed forward compensation.Finally,the benefits from the adaptive controller are analyzed and validated by numerical simulations.

2.Perturbed attitude dynamics of the platform of a TSR

2.1.System description

As shown in Fig.1,the TSR system under consideration is composed of a platform and debris of mass m connected by a straight massless tether,which is only capable of exerting force along the straight line connecting the debris.The debris is considered as a passive object without any active control.The tether’s unstrained length and longitudinal stiffness are l and EA,respectively.When the system operates in its orbit,the elastic tether is always kept taut due to the stiffening effects from the gravitational gradient and centrifugal force,and the stiffness-caused longitudinal elongation is characterized by ξ,which is defined as

Fig.1 Illustration of a Post-capture TSR system.

where Δl denotes the tension-caused elongation.

Furthermore,for simplicities,the following assumptions are also made during system dynamics development:(1)the system moves in a well-known non-eccentric orbit;(2)the passive debris is treated as a mass point and its attitude motion is beyond the scope of this work;(3)the mass of the debris is much smaller than that of the platform,and thus,the orbit center of the whole system can be assumed to coincide with the mass center of the platform;(4)the distance from the tether’s attach point to the mass center of the platform is much shorter than the length of the tether,(5)environmental perturbations,such as atmosphere resistance,earth oblateness,and sun pressure,are all neglected.

The reference frames used for dynamics modeling are also shown in Fig.1.The Earth inertial frame,represented by Oxyz,is a non-rotating frame with the origin point fixed at the mass center of the Earth.The local vertical local horizontal(LVLH)frame,represented by Oxoyozo,is a rotating frame,and its origin is located at the mass center of the platform.xo-axis is aligned with the orbital velocity,zo-axis is aligned with the vector from the Earth’s center to the mass center of the spacecraft,yo-axis is finally completed by following the right-hand principal.The body- fixed frame,denoted as Oxbybzb,is the frame to describe the attitude of the platform with respect to the LVLH frame.

2.2.Tether libration

In this section,elastic tether liberation equations will be developed within the LVLH frame,and the in-and out-of-plan librations and the tether longitudinal oscillation will also be described by the developed equations.Generally,to derive the equations of tether librations,the most effective approach seems to be the Lagrangian technique.The following equation represents Lagrange’s formula which provides an energy method based on finding expressions for the kinetic energy and generalized forces:

where qjand Qidenote the generalized coordinate and corresponding generalized force,while T and V represent the kinetic energy and potential energy,respectively.Seeing the geometric relations in Fig.1 and considering the 4th assumption,the position vector of the debris in the LVLH frame,denoted by ρ,can be approximately expressed as

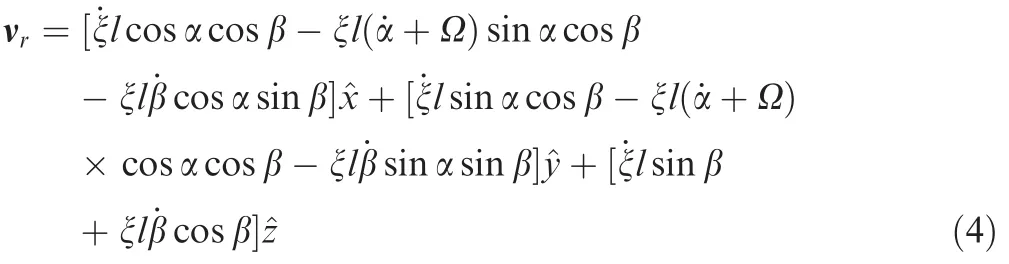
where Ω = ［0，-Ω，0］Tis the orbit velocity vector.Further,the absolute velocity of the debris with respect to the inertial frame can be calculated as

where vodenotes the orbital velocity,and in case of a circular orbit,it can be computed as

where R is the orbital position vector of the system and‖R‖=R.Then,the kinetic energy term can be written as

where M0is the total mass of the system.Then by substituting Eq.(4)and Eq.(6)into Eq.(7),one can obtain the explicit expression of the kinetic energy.To save the length of the paper,the kinetic energy expression will not be represented in detail.Next,the gravitational potential energy of the system can be formulated as

where μeis the constant gravitational coefficient.With Eq.(3),expandinginto a Taylor series and neglecting the highorder terms lead to

Then substitute Eq.(9)into Eq.(8),and the expression of the gravitational potential energy can also be achieved as

Additionally,consider the tether elastic elongation,the elastic potential energy terms can be written as

By combining Eq.(10)and Eq.(11),the total potential energy can be expressed as

Finally,applying Lagrangian equations with the expressions of the kinematic energy and the gravitational potential,the nonlinear equations for the tether libration can be formulated as

where c denotes the damping ratio of the tether,Fαand Fβare the non-dimensional forces for the in-and out-of-plane librations,while Flrepresents the external force acted along the tether.Eqs.(13)–(15)clearly indicate that the dynamics of the elastic tether are seriously nonlinear and coupled,so any perturbation acted on the system evidently leads to a longitudinal oscillation,and,as a result,generates an oscillated tensional force.Under the assumption of d≪l,then the tether tensional force vector,denoted as F,can be written within the body- fixed frame as

where Flis the tether tensional force,which can be calculated as

where Cobis the transformation matrix from the LVLH frame to the body- fixed frame,which can be calculated in terms of Euler angles of yaw ϑ,pitch θ,and roll ψ.When the platform is well controlled,the transformation matrix can be approximated as Cob≈ I3×3,in which I3×3∈ R3×3denotes the identity matrix.Meanwhile,

where f is the true anomaly of the system.Substituting Eq.(19)into Eq.(16),the tensional force for the inelastic tether can also be achieved as a vector within the LVLH frame.Peyman and Hassan27proposed an anti-sway control method to damp the attitude librations of main spacecraft,and the success of their method depends on accurate measurements of tether tension and in-plane libration angles;however,if the measurements are badly corrupted by inherent noises,the control performance will be significantly degraded.

2.3.Attitude dynamics of the platform

Next,the perturbed attitude dynamics of the platform will be derived by incorporating the tether-generated disturbance.Generally,by considering the platform as a rigid body,its nonlinear attitude dynamics can be given as

where J ∈ R3×3denotes the positive-definite inertia matrix,ω = ［ω1，ω2，ω3］Tindicates the angular velocity of the platform with respect to the inertial frame,and ω×denotes the skew-symmetric matrix of ω which can be calculated as

where uc∈R3is the active control torque,while ud∈R3denotes the disturbance torque caused by the librating tether.Here,it is worthy to note that the gravitational gradient disturbance torque will not be considered since it is much smaller than the tether-generated one.As shown in Fig.1,the disturbance torque can be written as

where d is the position vector of the attach point in the body fix frame.

Substitute Eq.(22)into Eq.(20),and then the perturbed attitude dynamics of the platform can be represented as

where ω×represents the skew-symmetric matrix of ω .Modified Rodrigues parameters(MRPs)are used to formulate the kinematics model of the platform,in which the MRPs represent a minimal parameterization with a singularity at 360°,avoid the normalization constraint associated with quaternion parameterization,and allow for rotations of greater than 180°.The attitude kinematics of the platform can be represented as

where σ×represents the skew-symmetric matrix of σ .The rotation matrix from the LVLH frame to the body- fixed frame is

3.Gyros-based disturbance observer

3.1.Gyros-based observer

As Eq.(22)shows,the attitude of the platform is always subjected to tether-generated perturbation,which adversely degrades the attitude stabilization performance after the debris capture.To stabilize the platform precisely,it is significantly important to develop a robust controller against the perturbation.Although Eq.(22)reveals that the disturbance torque could be obtained by measuring the vector of the tether tensional force,necessary sensors for the measurement,such as a tension sensor and a camera(measuring the liberation angle),will greatly complicate the system,and in addition,if measurements are badly corrupted by inherent noises,the control performance will be significantly degraded.In this section,a nonlinear disturbance observer(DO)will be developed to esti-mate the disturbance acted on the platform,and in the context,the proposed observer will be used to compensate for the disturbance torque by incorporating it into the control loop.The basic disturbance observer is constructed as follows:

As Eq.(28)shows,when the disturbance varies slowly via time,it is easy to find an appropriate Ψ and guarantee the estimation error to be bounded.Substituting Eq.(20)into Eq.(27),the basic disturbance observer can be expressed as

where φ（ω）is a vector function defined as

where Γ is a positive definite 3 × 3 matrix to be determined.Substituting Eq.(30)into Eq.(29),the basic observer can be reformulated as

Substituting Eq.(31)into Eq.(32),then we have

By examining the right-side terms,if the following conditions hold:

then the term associated with the angular acceleration can be canceled from the expression in Eq.(33),and the disturbance observer can be reconstructed as

Eqs.(35)and(30)provide a type of disturbance observer that only depends on ω,which could be acquired by using gyros with high qualities,and moreover,from Eqs.(30)and(35),it can be proven that the reduced-order observer has similar error dynamics to those of the basic one.

3.2.Observer stability

As Eq.(28)shows,the error dynamics are always affected by the disturbance rate,so in the following,the stability of the disturbance observer will be discussed based on Lyapunov stability criterion.Define the positive definite matrix as

In general,it is not difficult to find a positive matrix Mpthat satisfies

Then construct the Lyapunov candidate function as

Since both P and PTP are positive definite,thus the scalar function V（ω）is positive definite.Taking the first order of derivative with respect to time yields

For the time-varying disturbance,we suppose that the disturbance rate is bounded as

where τ is a constant real number.Eq.(30)is substituted into Eq.(39),and

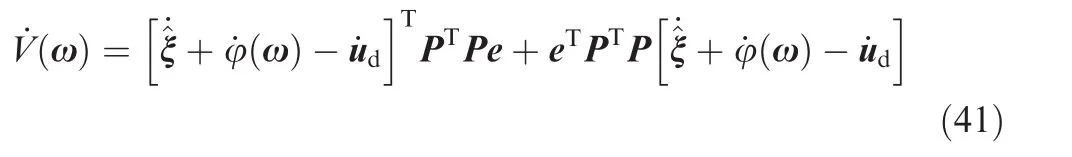
Further,with Eqs.(34)and(35),Eq.(41)can be rewritten as

Additionally,from Eq.(37),further yield

On the other hand,by employing Rayleigh inequality,it shows that the Lyapunov candidate function expressed in Eq.(38)is bounded as

Applying Rayleigh inequality,the inequality Eq.(43)can also be rewritten as

Combining the inequality Eq.(46)with the inequality Eq.(47)leads to

With the disturbance boundary inequality Eq.(40),then applying the Schwartz inequality yields

Then combining Eq.(47)with Eq.(49),we have

Define γ as

Then with Eq.(51),the inequality Eq.(50)can be reformulated as

Form the expression Eq.(46),if γ＞ 1,

which means that the error is always bounded,while for the case of 0≤γ≤1,

With Eq.(46),then we have

From Eq.(53)and Eq.(55),it can be confirmed that the error is always bounded.Furthermore,from Eq.(55),we can also get

where t denotes time.Further,substituting Eq.(56)into Eq.(44)and combining with Eq.(54) finally yield

The inequality Eq.(57)reveals that in case of time-varying disturbance,the error converges with an exponential rate of-and the steady error is bounded by the termConsidering the special case that both Γ and J are diagonal matrices,it is simple to find that by increasing the eigenvalues of Γ,the steady-state boundary of the disturbance estimation will be decreased,and accordingly,a more accurate estimation could be achieved.

4.Composite attitude controller

4.1.Structure of the composite attitude controller

With the purpose of stabilizing the attitude libration of the platform,a composite controller is proposed in this section.As shown in Fig.2,the basic structure of the composite controller(also named DO-based controller)consists of a feedback control loop and an observer-based feedforward compensation loop.The feedback control loop,which involves a sliding mode controller,works to stabilize the attitude motion,while the feedforward compensation loop’s task is to reject the disturbance torque caused by the librating tether.

4.2.Sliding mode controller

Sliding mode control is a type of variable structure control method that alters the dynamics of a nonlinear system.Rather than continuous controllers,a sliding mode controller switches from one continuous structure to another based on the current system state,with a discontinuous control force,and the system could be guaranteed to slide within the vicinity of prescribed switching manifolds.The major advantage of sliding mode control is low sensitivity to the uncertainties of system parameters and external disturbances.Although the proposed gyros-based disturbance observer has been adopted for closedloop control,still there is the residual disturbance,which is determined by the disturbance estimation error,that imposes a negative effect on the control performance.Therefore,by using sliding mode control,the attitude control performance could be further enhanced due to the robustness of a sliding mode controller against the residual disturbance.

By using the MRPs,the sliding manifolds are given as

where σdis the desired orientation,Λ is a diagonal matrix with negative elements,and G-1（σ）is calculated as follows:

Fig.2 Illustration of a closed-control loop structure.

Under a perfect control,the attitude of the platform moves on the surface of s=03×3.To enable decoupled sliding motions and exponential convergence toward the expected orientation,the sliding mode controller is constructed as

where Ksis a 3×3 positive definite diagonal matrix,ε is a small positive scalar,while sat（s，ε）represents the saturation used to minimize the chattering in the control input and is defined by

The attitude stabilization problem requires the final orientation with respect to the LVLH frame to be zero,and then the final desired orientation can be given as σd=0.To simplify the controller construction,the matrix Λ is assumed to be given by

Then Eq.(59)can be rewritten as

Eq.(64)can be further simplified significantly by taking some cross product operation,which leads to

Then taking the first order of derivative with Eq.(65)yields

Substitute Eq.(66)and Eq.(65)into Eq.(61),and finally the sliding mode controller can be completed.In addition,it is not difficult to prove the stability28of the controller by selecting a proper Lyapunov function.

5.Numerical results

In this section,the effectiveness of the proposed composite control scheme is validated by series of numerical simulations.The numerical model of a TSR after debris capture is constructed within Matlab,and the gyros-based disturbance observer and sliding mode controller are also incorporated into the control loop.For the purpose of comparison,the control performance in absence of the disturbance observer,so-called non-DO controller,is also investigated.Meanwhile,due to the disturbance estimation accuracy which significantly depends on the selected eigenvalues for the observer gain matrix,the sensitivities on the variation of the observer gain are also discussed based on numerical results.To facilitate the analysis on the observer performance,the uncertainties of gyros measurement are not considered.The entire simulation takes one orbit resolution,and the time step is set to be 1s.The parameters associated with the simulations are listed in Table 1.

Like the longitudinal libration,the post-capture system is supposed to experience both in-and out-of-plane librationsbecause of the non-zero relative velocity of the debris at the capture moment.The initial librations are described by the tether’s initial conditions listed in Table 1.It should be noted that,because the out-of-plane libration is unstable,therefore,during the simulation,a passive out-of-plane libration damper is assumed to void the continuous tumbling of the post-capture system,and both the libration angles and tether tensional force are also treated as unknown terms.Only the attitude angle velocities are measured by using gyros,and no active control is acted on the captured debris and the librating tether.

Table 1 Simulation parameters.

As shown in Fig.3,the libration trajectory of the captured debris is represented with respect to the LVLH frame,which clearly shows that the libration always remains bounded within the whole simulation,and the maximum libration amplitudes on both x and y directions are 10 m and 40 m.The in-and out-of-plane libration angles are also depicted in Fig.4.

Due to the dynamic coupling,the in-and out-of-plane librations naturally lead to a longitudinal libration and generate a tensional force on the connecting tether.The tensional forces for elastic and inelastic tethers are both presented in Fig.5.For the inelastic tether,the tensional force varies slowly within a range from 3 N to 4 N,while for the elastic tether,the tensional force dramatically oscillates around the tensional values of the inelastic tether,but the oscillation is gradually suppressed by the passive damping of the tether.The results for the tether tensional force illustrate that by comparing with the inelastic case,the disturbance generated by the elastic tether becomes more serious regarding to high-frequency longitudinal libration.Although by suffering a longitudinal oscillation,the tensional force remains positive and reveals that the tether is always maintained taut during the libration.Fig.6 shows the attitude motion of an uncontrolled platform;obviously,the platform becomes unstable under the disturbance from the librating tether.

Fig.3 Libration trajectory of the captured debris in the LVLH frame.

Fig.4 In-and out-of-plane libration angles.

To attain the unknown disturbance torque acted on the controlled platform,the proposed gyros-based observer is used for disturbance estimation.The estimated disturbance torque,as well as the modeled ones from Eq.(8),is simultaneously plotted in Fig.7.Since the tether attach point is located on the yaw axis of the body- fixed frame,the modeled disturbance torque component along the yaw axis always remains zero.From the results,one can see that the observer response,which is depicted with a red dash line,tracks the modeled disturbance accurately despite the initial short-term oscillation on the yaw axis.Actually,the short-term oscillation corresponds with the convergence of the observer from the initial condition to the true value,and it can be regulated by choosing different gain matrices and initial conditions for the disturbance observer.

Fig.5 Tensional force of the connecting tether.

Fig.7 History of disturbance estimation.

Fig.8 Errors of disturbance estimation.

The disturbance estimation errors are shown in Fig.8.One can see that the error along the yaw axis nearly falls to zero,while the ones along the pitch and roll axes gradually converge to zero,but they are subjected to high-frequency oscillations.Recalling the results from Fig.7,in addition to the highfrequency oscillation,the disturbance component along the pitch axis also experiences long-term variation,which results in a faster time-varying rate than that along the roll axis.Finally,according to Eq.(40),if all the observer parameters are fixed,the estimation error uniquely depends on the timevarying rate of the disturbance;hence,the estimation error along the pitch axis is greater than that along the roll axis.

In order to suppress the induced attitude libration from the connecting tether,the DO-based controller,which involves the disturbance observer within the control loop,is applied for the platform.In fact,the control torques,as shown in Fig.9,represent the combination output of the disturbance compensation and the sliding mode controller.From the result,one can see that the control torques nearly equal to the disturbance torque shown in Fig.7,which reveals that the control effort is mostly dedicated to the disturbance compensation.

Fig.9 Control torques of the DO-based controller.

Fig.10 Attitude control error of the platform.

Fig.11 Attitude control errors with different observer gain matrices.

The attitude control errors of the platform for both DO-based control and non-DO-based control cases are represented in Fig.10,in which obviously,the results represent the most important evidence that proves the benefits from the disturbance observer can be confirmed by incorporating the disturbance observer into the control loop,and finally,the control precision for attitude stabilization is remarkably enhanced.The negative effects from the tether-generated disturbance torque are effectively migrated after introducing the disturbance compensation,which illustrates the performance promotion of the attitude control system of the platform.

The quality of disturbance estimation significantly affects the DO-based control performance:the higher accuracy of disturbance estimation is,the better performance can be achieved.As analyzed earlier in Eq.(40),the eigenvalues of the observer gain matrix affect the disturbance estimation errors inherently.To validate the dependence of control accuracy on the observer gain matrix,the results in Fig.11 are dedicated to illustrate the control errors with different observer gain matrices;one can observe that with variations of the eigenvalues of Ψ from λi=0.2 to λi=0.1,the platform suffers degradation on control accuracy.The results also indicate that for higher stabilization accuracy expectation,greater eigenvalues should be selected to construct the observer gain matrix.

6.Conclusions

A spacecraft with tether-captured debris is a typical nonlinear system that is perturbed by a disturbance torque.Robustness against the disturbance is an important property required for platform attitude stabilization.With the purpose of improving the attitude stabilization accuracy,a gyros-based disturbance observer is proposed and incorporated into the control loop to compensate the tether-generated disturbance torque.The gyros-based disturbance observer only depends on the measurements of attitude angular velocities.Theoretical and numerical analysis indicates that compared with the case of non-observer-based control,the disturbance observer-based controller achieves remarkable performance promotion.Moreover,the dependence of control accuracy on the observer gain matrix is also validated by numerical simulations.

Acknowledgements

The authors are grateful to the editors and anonymous reviewers for their many constructive and helpful comments.This work was supported by the National Natural Science Foundation of China(11102018).