Damage localization eあects of the regenerativelycooled thrust chamber wall in LOX/methane rocket engines

Jiawen SONG,Bing SUN

School of Astronautics,Beihang University,Beijing 100083,China

KEYWORDS

Abstract To investigate the damage localization effects of the thrust chamber wall caused by combustions in LOX/methane rocket engines,a fluid-structural coupling computational methodology with a multi-channel model is developed to obtain 3-demensioanl thermal and structural responses.Heat and mechanical loads are calculated by a validated finite volume fluid-thermal coupling numerical method considering non-premixed combustion processes of propellants.The methodology is subsequently performed on an LOX/methane thrust chamber under cyclic operation.Results show that the heat loads of the thrust chamber wall are apparently non-uniform in the circumferential direction.There are noticeable disparities between different cooling channels in terms of temperature and strain distributions at the end of the hot run phase,which in turn leads to different temperature ranges,strain ranges,and residual strains during one cycle.With the work cycle proceeding,the circumferential localization effect of the residual strain would be significantly enhanced.A post-processing damage analysis reveals that the low-cycle fatigue damage accumulated in each cycle is almost unchanged,while the quasi static damage accumulated in a considered cycle declines until stabilized after several cycles.The maximum discrepancy of the predicted lives between different cooling channels is about 30%.

1.Introduction

In the twenty- first century,the market of the space launch industry is unceasingly increasing.According to the state of the satellite industry report presented by the Satellite Industry Association(SIA),the global revenues from commercial satellite launches in 2015 were estimated to be about 5.4 billion dollars,but there were only 65 launches worldwide throughout the year.1To make access to space less expensive,many countries have focused on Reusable Launch Vehicles(RLVs)in recent years to replace expendable ones.2Reusable Liquid Rockets(RLRs)are regarded as a practicable target for the present due to inheritable technologies,high thrusts,and low costs.3The propellant combination of Liquid OXygen(LOX)and methane has aroused interests in the aerospace community because of its advantages over conventional propellant combinations,such as high-density specific impulse,super maneuverability,and convenience for manufacture.4In an Interplanetary Transport System (ITS)proposed by SpaceX,LOX/methane rocket engines are considered as candidates for both first and second stages of an RLR.5In addition to the performance,the reusability must be available,if LOX/methane engines are applied to an RLV.It is necessary to extend the lifetime of LOX/methane engines on the basis of conventional expendable ones.Therefore,mitigating the damages of key components during operation is indispensable for the design of LOX/methane engines.6

As one of the key components,the thrust chamber is subjected to severe heat flux from the combustion of propellants,especially in the near-throat region.General materials could hardly survive from such heavy heat loads.Regenerative cooling achieved by flowing a liquid propellant into suitable cooling channels,which are machined in the thrust chamber wall,has been extensively used to maintain the thrust chamber.For LOX/methane thrust chambers,cryogenic methane is chosen as the coolant due to its superior cooling properties,higher coking limits,and less soot deposition.7,8Traditional cooling channels are milled in the copper liner and closed out by a nickel jacket through electroforming processes.9Quentmeyer10conducted experiments to explore the failure of the thrust chamber wall under cyclic work,and results indicated that a‘doghouse’-shaped failure characterized by the thinning and bulging of the inner wall appeared after several cycles.Jankovsky et al.11pointed out that potential failure factors are low-cycle thermal fatigue,thermal–mechanical ratcheting,and creep rupture.

Quantifying the damage of the thrust chamber wall is significant for the design of RLRs.Much research has been performed on this urgent problem to promote the practical use of LOX/methane engines.Miller12performed a plane strain finite element analysis for the throat section of a thrust chamber to identify the strain range of the thrust chamber wall under cyclic work.The low-cycle fatigue life of the thrust chamber wall was estimated based on isothermal fatigue test data.Arya and Arnold13employed Robinson and Swindeman’s viscoplastic model14to predict the stress and strain on the cross section of an experimental cylinder chamber wall,and the‘doghouse’-shaped failure observed in experiments10was qualitatively replicated.Yang et al.15performed a plane strain structural analysis with Robinson and Swindeman’s model to explain the damage process of the chamber wall.Their numerical results revealed the effects of startup and shutdown durations on predicted lives.Robinson and Swindeman’s model considers the creep strain at high temperature and its interaction with the plastic strain.However,this model uses a single internal state variable to represent the kinematic hardening behaviors of materials.Thus it is not applicable to modeling the cyclic plasticity and then estimating the damage caused by ratcheting.Riccius et al.16,17predicted the life of a Thermo-Mechanical Fatigue(TMF)panel based on the strain differences calculated by the Chaboche nonlinear kinematic hardening model,18which could accurately capture the ratcheting behavior of the copper liner under cyclic loading.Ferraiuolo et al.19used a simplified viscoplastic model combining an elastoplastic model with Norton’s creep law to investigate the nonlinear deformation of the inner liner.

Although much work has been carried out on the development of constitutive models for the copper liner,only little attention has been devoted to the nonlinear stress–strain responses of the inner wall under comprehensive Three-Dimensional (3-D) loads. In fact, injectors lead to substantial circumferential variations of the heat flux on the hot-gas-side wall.20,21The effects on the deformation and damage of the copper liner have not been well understood.The classical half-channel geometrical model simplified based on the circumferential periodicity of cooling channels cannot be competence in revealing them.Until recently,Riccius et al.17performed a thermal-structural finite element analysis with a three-channel plane strain model simplified based on the layout of the injectors in the outer row.Results indicated that circumferential differences of the heat flux caused the localization effects of damages characterized by a rapid increase of the damage in one of the cooling channels.As a consequence,the three channel model obtained a much shorter life than that by the half-channel model.However,assumed thermal boundary conditions were applied in their studies,instead of realistic heat loads obtained by experiments or numerical computations.

In this paper,the damage localization effects of the thrust chamber wall caused by combustions in LOX/methane rocket engines are characterized by a fluid-structural coupling computational methodology.Heat and mechanical loads are obtained by a validated finite-volume fluid-thermal coupling numerical method,in which the non-premixed combustion processes of propellants are simulated by a non-adiabatic flamelet model considering real- fluid properties.A nonlinear thermal structural finite element analysis is subsequently performed to obtain 3-D stress–strain responses of the thrust chamber wall under cyclic operation.To account for the influences of injectors,a multi-channel geometrical model simplified based on the layouts of injectors is employed.With numerical results,a post-processing damage analysis is performed to determine the service life of the thrust chamber wall.Ultimately,the effects of heat flux non-uniformity in the circumferential direction on the damage are discussed in detail.The modeling technique proposed in this paper may significantly improve the accuracy of the predicted lifetime of the thrust chamber wall.Moreover,the results presented here would provide engineers better insight to design the reusable thrust chamber of LOX/methane engines effectively.

2.Computational methodology

A typical sub-scale thrust chamber of LOX/methane rocket engines is investigated in the present paper.The geometrical parameters of the thrust chamber are available in our previous work.22Fig.1 shows the transverse section of the injectors in the chamber head and the cooling channels in the chamber wall.The chamber head consists of 18 shear-coaxial injectors.Meanwhile,30 cooling channels are milled axially in the inner liner.Because the layouts of injectors and cooling channels are periodic in the circumferential direction,the thrust chamber is reduced to 30°in the following computations by employing symmetrical boundary conditions,as shown in Fig.1.

Fig.1 Layouts of injectors and cooling channels.

Fig.2 shows the calculating procedure used in this paper.In Fig.2,Twgand qwgare the temperature and heat flux of the hot-gas-side wall,respectively.For reusable LOX/methane engines,a full work cycle consists of four phases including pre-cooling,hot run,post-cooling,and relaxation.Because the life of the thrust chamber wall is mainly limited by thermal induced inelastic strains at severe temperatures,a nonlinear thermal-structural analysis of the thrust chamber wall must be performed to estimate the service life.To make computations more effective and robust,we suppose that the flow and heat transfer are not influenced by the deformations of solid domains.Therefore,one-way coupling can be applied to the thermal-structural analysis.A precise fluid-thermal coupled heat transfer calculation considering combustion and regenerative cooling during the hot run phase provides requisite convection and mechanical loads for the thermalstructural analysis.

Fig.2 Schematic of calculating procedure.

2.1.Fluid-thermal calculation

The coupled heat transfer in the regeneratively-cooled thrust chamber consists of three key parts:(A)the heat transfer between the hot gas and the inner wall,(B)the heat conduction across the chamber wall,and(C)the convective heat transfer between the chamber wall and the coolant.In order to precisely obtain the temperature of the chamber wall,we could compute all three parts concurrently.However,this procedure may increase computational spending and numerical instability.A fluid-thermal coupling strategy in our previous work23is adopted in this study to deal with the conjugate heat transfer between the hot gas,the chamber wall,and the coolant.This strategy is characterized by relatively low computational spending and high numerical stability.

For an LOX/methane thrust chamber working over supercritical pressures,the transcritical flow behavior of injected oxygen in the near-injector region24results in dramatic changes of properties such as density and specific heat capacity even with small changes of temperatures and pressures.25In these processes,continuous mixing of propellants controlled by turbulent diffusion instead of atomization and vaporization was observed by published experiments.26The mixing and combustion of LOX/methane are greatly influenced by the so-called pseudo-boiling phenomena.24

In our previous work,23a non-adiabatic flamelet model considering real- fluid properties and finite-rate chemical reactions was developed to solve the non-premixed combustion of LOX/methane.In the flamelet model,turbulent flame is defined as an assembly of thin,laminar,locally onedimensional flamelet structures present within a turbulent flow field.Laminar diffusion flame equations can be transformed from a physical space to a mixture fraction space.27For non-adiabatic systems,equations of temperature,mass fractions of all species,and total enthalpy are solved.The solutions to flamelet equations are preprocessed by the CHEMKINCFD module.After that,mean scalars are stored in look-up tables through a series of logical steps,as Fig.3 depicts.In Fig.3,φ represents the temperature and species mass fractions,p is a probability density function,H is the specific enthalpy,f is the mixture fraction,and χstis the stoichiometric scalar dissipation rate.More details can be found in Ref.23.The flamelet model was validated by published experiments.26The validation suggested that the model could successfully describe the mixing and combustion processes for LOX/Methane thrust chambers with single-injector elements.The flamelet model was embedded in the fluid-thermal coupling calculation.Final simulation results for a thrust chamber with multi-injector elements have been compared with the results of finite-rate chemistry(eddy dissipation concept model)and the Bartz equation.The comparisons demonstrated that this method could obtain a more accurate and comprehensive 3-D temperature field.The results of this method also suggested that the transcritical combustion has a strong influence on the heat flux of the chamber wall.

Fig.3 Steps of look-up table generation.

In the subsequent research work,22the flamelet model was significantly improved to make it capable of predicting the heat transfer in thrust chambers quantitatively.The detailed chemical kinetic mechanism Ref.28was employed to model methane-oxygenfinite-rate chemical reactions.The Chung et al’s method29was embedded in the CFD solver by User Defined Functions(UDFs)to accurately predict thermophysical properties of the coolant,propellants,and hot gas.The validity and practicality of the calculation were assessed by a published test,30and numerical results were confirmed to be close to experimental heat flux data.With the sophisticated fluid-thermal coupling calculation method,the convection and mechanical loads on the fluid–solid interface surface can be thoroughly obtained.Therefore,the method was employed in this work to determine the loads for the following thermal-structural analysis of the thrust chamber wall.

Calculations were performed by applying the overall oxidizer-to-fuel mixture ratio O/F=3,and the pressure of the combustion chamber was 7 MPa.The inlet temperatures of the oxidizer and fuel streams were 120 and 300 K,respectively.The mass flow rates at the inlets of propellants were deduced by the NASA Chemical Equilibrium with Applications(CEA)program.At the coolant inlet,the mass flow rate was 2.2 kg/s,the static temperature was 120 K,and the static pressure was 11 MPa.

2.2.Thermal-structural analysis

2.2.1.Governing equation

The transient heat conduction of the thrust chamber wall is governed by

where ρ is the density,c is the specific heat capacity,k is the thermal conductivity,T is the temperature,and t is the time.The expression of the total strain is given by

where ε is the total strain, εthis the thermal strain, εelis the elastic strain,and εplis the plastic strain.Since thermal expansions of materials only cause normal strains,thermal strains for isotropic materials can be written as

where α is the isotropic secant coefficient of thermal expansion,and Trefis the reference temperature.The relationship between the elastic strain and the stress is described by generalized Hooke’s law as

where D is the elastic stiffness matrix,and σ is the stress.

The employed constitutive model for the cyclic plastic behavior of the inner liner is a rate-independent version of the kinematic hardening model proposed by Chaboche.18The constitutive equations are based on the von Mises yield criterion,the associated flow rule,and a nonlinear kinematic hardening law.All the model parameters have been carefully defined in our previous work.31

2.2.2.Numerical treatments

The numerical discretization and solving of the governing equations were executed by the ANSYS Parametric Design Language(APDL),32which is based on the finite element method.The overall equilibrium equations for transient thermal and static structural analysis are expressed as Eqs.(5)and(6),respectively.

where T is the temperature matrix,C is the specific heat matrix,K is the conductivity matrix in Eq.(5)or the total stiffness matrix in Eq.(6),Q is the applied heat flux,u is the displacement matrix,Fais the total applied load vector,and Fris the reaction load vector.

Owing to the inelastic relationship between stress and strain,coupled with the temperature-dependent material properties,the coefficient matrices(C and K)are functions of the unknown Degree Of Freedom(DOF)values(T and u).Consequently,Eqs.(5)and(6)are nonlinear equations.The incremental Newton–Raphson approach,33which performs iterations at each step until convergence is achieved,was used to solve nonlinear equilibrium equations.

In Eq.(5),the generalized trapezoidal rule34is assumed to predict the nodal DOF values at the next time step,which can be described as

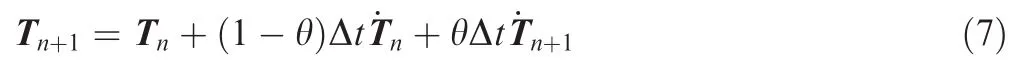
where Tnis the nodal temperature at time tn,˙Tndenotes the time rate of the nodal temperature at time tn,and θ is a transient integration parameter.

2.2.3.Grid generation and boundary conditions

In the finite element method,the geometry being computed must be approximated as an assembly of a finite number of elements connected by nodes.Three-dimensional,twenty-node solid elements applicable to both thermal analysis and structural analysis were generated in the computational domain.The elements employ higher-order interpolation functions33so that precision can be ensured with a relatively coarse mesh.A close-up shot of the computational grid is shown in Fig.4.

The initial temperature of the thrust chamber wall was equal to room temperature(295.15 K).The schematic of boundary conditions is shown in Fig.4,where T is the bulk temperature of the fluid,H is the convective film coefficient,and P is the pressure of the fluid.The subscripts ‘hot’,‘cool’,and ‘out’represent hot-gas-side,coolant-side,and out-side,respectively.Specified convective boundary conditions acted over the fluid–solid coupled wall surface.For symmetric surfaces,adiabatic boundary conditions were employed.

Table 1 shows the specific values of convective boundary conditions for transient thermal analysis.Both the values of Toutand Houtremained constant during the whole work cycle to model the sustained natural convection between the out-side wall surface and air.The convective film coefficients and bulk temperatures on the coupled wall surfaces obtained by the fluid-thermal coupling calculation described in Section 2.1 were used as convective boundary conditions during the hot run phase.Meanwhile,the convective loads on the coupled wall surfaces were assumed to be homogeneous during the other phases.It should be noted that the mass flow rate of the coolant during the pre-cooling and post-cooling phases is 1 kg/s.Accordingly,Hcoolduring the pre-cooling and postcooling phases can be deduced by the Gnielinski equation,35which is given by

Fig.4 Mesh and boundary conditions.

where Nu is the Nusselt number,Re is the Reynolds number,and,Pr is the Prandtl number.In addition,fDis the Darcy friction factor obtained from the correlation developed by Petukhov36as follows:

For the near-throat region,a cooling enhancement factor equal to 1.4 was employed to account for the influence of Dean vortices developing in the curved channel.9The Nusselt number obtained by Eq.(8)was multiplied by this factor to improve the accuracy.Meanwhile,all the convective film coefficients of natural convection in the thermal analysis were estimated to be 10 W/(m2·K).This value is consistent with the fact that the film coefficients of natural convection should be much smaller than those of coolant convection.

In the succeeding nonlinear structural analysis,the symmetric surfaces marked in Fig.4 were prevented from moving in the normal direction.The pressure distributions on the coupled wall surfaces obtained by fluid-thermal coupling calculations were applied as the mechanical loads during the hot run phase.For the pre-cooling and post-cooling phases,the uniform mechanical loads on the hot-gas-side wall were assumed to be normal atmospheric pressure,while the pressures on the coolant-side wall were 3 MPa.For the relaxation phase,all the mechanical loads were normal atmospheric pressure.On the other hand,the temperatures of the thrust chamber wall at each time step obtained by the transient thermal analysis were applied as thermal body loads.

The results independent of the finite element model will be adopted in the following research,which were obtained by comparison of the stress–strain responses of the identical location predicted with various grid levels and load sub steps.31

3.Results and discussion

With the fluid-thermal coupling calculation method,the heat flux of the entire thrust chamber wall influenced by transcritical mixing and combustion processes could be obtained.Fig.5 illustrates the predicted distribution of the heat flux on the hotgas-side wall with an azimuth angle of 30°.The wall heat fluxes near the throat region are much greater than those in other regions,which suggests that the chamber wall in the nearthroat region operates in harsh environments of extremely strengthened heat loads.As a result,the failure of the thrust chamber wall probably occurs in this region.Moreover,Fig.5 shows that the heat flux is highly non-uniform in the circumferential direction due to the effects of the layout of multielement injectors,which has been fully detailed in Ref.23.To predict the life of the thrust chamber precisely and efficiently,a 3-D thermal-structural analysis of the near-throat region with an azimuth angle of 30°should be conducted in this study.That is why two and a half cooling channels were included in the computational domain,as Fig.4 shows.

3.1.Transient thermal analysis

Fig.6 depicts the temperature distribution of the thrust chamber wall near the throat region at the end of the hot run phase.It should be noted that the hot gas flows in the+z direction.As Fig.6 shows,the inner wall in the throat region and its upstream area are under extreme high temperatures.Nonetheless,the temperatures in the inner wall are well below the service limit of copper alloy because of the effective cooling of cryogenic methane in cooling channels.The maximum temperature(536 K)is significantly lower than that of expendable chambers,but it is suitable for reusable chambers to achieve longer service lives.On the other hand,regenerative cooling brings about huge temperature differences across the thrust chamber wall during the hot run phase.It is clearly shown in Fig.6 that the temperatures in the outer jacket remain relatively low values because most of the heat from the combustion is absorbed by the coolant.

Table 1 Boundary conditions for thermal analysis.

Fig.5 Heat flux distribution of hot-gas-side wall.

Fig.6 Temperature distribution at end of hot run phase.

Fig.7 shows the temperature distributions of the chamber wall at the end of the hot run phase on the cross section where the maximum temperature appears.It can be observed that the circumferential non-uniformity of the temperatures in the inner wall is quite evident,which indicates that the thermal body loads of different cooling channels are not identical.For the cooling channels in this study,there are three kind of thermal body loads.However,the traditional thermalstructural analysis is generally based on a half-channel model with the assumption that the hot gas is almost homogeneous in the circumferential direction,which contradicts the fact that the flow and heat transfer of the hot gas are seriously affected by the layouts of injectors even if the combustion process is sufficiently completed.The results here suggest that the influence should be taken into account when thermal-structural analysis is conducted.

Fig.7 Cross-section of temperature distributions in near-throat region.

Fig.8 Temperature histories at different points on hot-gas-side wall.

In the classical half-channel model,the maximum temperature of the chamber wall during the hot run phase appears at point D of the cross section,which is the intersection between the hot-gas-side wall and the centerline of the cooling channel.31Fig.8 presents the transient temperature responses of points D in different cooling channels marked in Fig.7.As Fig.8 shows,the temperature responses of points D1,D2,and D3follow the same pattern throughout the full cycle.However,discrepancies between the temperatures at these points are not negligible during the hot run phase due to the inconsistence in the hot-gas-side wall temperature (see Fig.7),while the temperature profiles are confirmed to be close during other phases.For the full cycle,the temperature variation ranges of these points are much different.These findings further imply that the structural responses of these channels should be diverse under cyclic work.

3.2.Nonlinear structural analysis

3.2.1.Distributions of stress and strain

Because the nickel jacket of reusable thrust chambers owns a much greater yield strength and works in a much narrower temperature variation range than those of the copper liner,31the outer jacket is much safer than the inner liner so that the stress and strain of the inner liner would be the focus of the following research.Fig.9 depicts the total circumferential mechanical strain distributions in the near-throat region at the end of each phase of the first cycle.As shown in Fig.9,large compressive strains appear in the inner wall during the hot run phase,while large tensile strains appear in the same place during other phases.The result can be explained by the huge temperature difference resulting from the application of regenerative cooling(see Fig.6).As both Figs.6 and 7 exhibit,the inner wall operates at much higher temperatures than those of the rib and outer jacket during the hot run phase.Hence,the inner wall tends to expand compared with the rib and outer jacket.As a result,the thermal deformations of the inner wall are constrained,which leads to large compressive strains in the inner wall.Conversely,the inner wall operates at much lower temperatures during the pre-cooling and post-cooling phases,which results in large tensile strains.This result is understandable because the thrust chamber is shut down,while the coolant is supplied to cool down the chamber wall.During the relaxation phase,the thrust chamber wall returns to room temperature because the coolant is cut off.Tensile strains are gradually reduced during the relaxation phase.Nevertheless,significant tensile strains still remain in the inner wall,especially in the near-throat region.

Fig.9 Total circumferential mechanical strain distributions during first cycle.

Fig.10 shows the cross sections of total circumferential mechanical strain distributions of the chamber wall where the maximum strain appears.As Fig.10 shows,the strain distributions of different cooling channels are almost similar during the pre-cooling phase.However,differences between these channels develop since the hot run phase.The reason for this phenomenon is that the hot-gas-side wall heat flux during the hot run phase is inhomogeneous in the circumferential direction which results in a localization effect of the temperature in the inner wall.Although heat loads tend to be uniform since the post-cooling phase,the localization effect of the strain during the hot run phase seems to be persistent during the last two phases.It is clearly shown in Fig.10(c)that terrific tensile strains are concentrated in one of these inner wall ligaments while relatively small strains remain in the other two inner wall ligaments during the post-cooling phase.The localization effect is moderately relieved but still evident at the end of the relaxation phase,as shown in Fig.10(d).

As we know,the half-channel model has been widely applied to 2-or 3-D finite element analysis to obtain the strain of the thrust chamber wall.However,the results of 3-D thermal-structural analysis with the multi-channel model in this paper suggest that there are noticeable disparities between different cooling channels in terms of strain distributions.In our opinion,it is quite necessary to use a reliable multichannel model in the thermal-structural analysis of the regeneratively-cooled thrust chamber wall to take into account the effects of multi-element injectors.

3.2.2.Stress–strain responses of the first cycle

The results presented earlier indicated that the circumferential localization effects of strains were quite obvious in the thrust chamber wall.In order to reveal the mechanism of the effects,stress–strain responses of the first cycle will be presented and discussed in this section.Fig.11 depicts the stress–strain response at the maximum circumferential residual strain point.As Fig.11 shows,the temperature differences across the chamber wall always tend to compress the inner wall during the hot run phase,and tensile the inner wall during the pre-cooling and post-cooling phases.These findings are understandable because both the temperature and secant coefficient of thermal expansion are mismatched in the chamber wall,which has been expounded earlier.The maximum strain of the inner wall appears in the convergent part of Channel 3,which operates at relatively low temperatures during the hot run phase compared with those of other channels.Meanwhile,the maximum temperature is located in Channel 1(see Fig.7).It seems abnormal that the maximum temperature and residual strain appear in different channels.Nevertheless,the inconsistency could be explained when combined with the stress–strain responses of these channels.Fig.12 shows the stress–strain curves of the maximum residual strain points in different cooling channels.The stress–strain curves show similar tendencies during one cycle.It can be noted from this figure that the curves exactly coincide during the pre-cooling phase.However,discrepancies of the curves between these channels develop since the hot run phase.Ultimately,these channels have distinct residual strains.Compared to other channels,the point of Channel 3 has a much smaller compressive strain at the end of the hot run phase,leading to a much greater residual tensile strain at the end of the cycle,although the temperature fields of these channels tend to be identical since the postcooling phase.Accordingly,these channels also own different strain ranges of the first cycle,because the maximum tensile and compressive strains appear during the pre-cooling and hot run phases(see Fig.11),respectively.

Fig.10 Cross-sections of strain distributions of chamber wall near throat region.

Fig.11 Stress–strain responses of the maximum residual strain point during the first cycle.

Fig.12 Stress–strain responses of different cooling channels.

According to the linear damage rule,the low-cycle fatigue damage of one cycle can be evaluated by

where Ncis the number of cycles to failure,which,according to the famous Manson-Coffin law,37is negatively correlated with the strain range.This result reflects the diversity of low-cycle fatigue damages among these channels,which is one of the typical characteristics of damage localization effects.On the other hand,only minor differences can be observed between the stress–strain curves of Channels 1 and 2.A possible explanation for this is that the temperature history of Channel 1 is very close to that of Channel 2,as shown in Fig.8.In other word,the deformation localization effect should be closely related to the temperature localization effect.These findings imply that the circumferential localization effect in the thrust chamber wall would be palliative if the combustion is almost perfect.In general,circumferential temperature differences of the chamber wall in the near-injector region are much more obvious than those in the near-throat region,even though a high combustion efficiency is achieved in the thrust chamber.Therefore,further research might focus on the localization effect in the cylindrical part of the thrust chamber.

3.2.3.Stress–strain evolutions for multiple cycles

For reusable thrust chambers working periodically,the thermal–mechanical ratcheting of the inner wall is a major factor affecting their service lives.To explore the features of ratcheting behaviors,3-D thermal-structural analyses were extended to ten work cycles.Fig.13 illustrates the circumferential strain distribution in Channel 3 at the end of the tenth cycle.To clearly display the deformation trend of the inner wall,the displacements of nodes are magnified by a factor of 100.As Fig.13 shows,the residual tensile strains concentrates in the ligament have significantly grown at the end of the tenth cycle.Meanwhile,the maximum residual strain is fixed in the same place after ten cycles.With the tensile strain accumulates,thinning and bulging of the inner wall can be observed,which is consistent with the experimental results obtained by Quentmeyer.10Fig.14 shows the circumferential stress–strain response at the maximum residual strain point during the initial five cycles.The stress–strain loop of each work cycle is very similar in shape,and the loop shifts along the x direction when the work cycle proceeds.Fig.15 presents the circumferential maximum strain,minimum strain,and strain range evolutions at the maximum residual strain point.As shown in Fig.15,both the maximum and minimum strains of the considered cycle increase when the work cycle proceeds.Since the strain range is defined as the difference between these two parameters,it has been consistently maintained.These results suggest that the low-cycle fatigue damage in each cycle calculated by Eq.(10)almost remains unchanged.Thus the low-cycle fatigue damage under cyclic operating could be estimated based on the nonlinear structural analysis of the first cycle.

Fig.13 Strain distribution in inner wall at the end of the tenth cycle.

Fig.14 Stress–strain responses at the maximum residual strain point during five cycles.

Fig.15 Maximum strain,minimum strain,and strain range at the maximum residual strain point.

Fig.16 shows the variations of circumferential residual strains at the maximum residual strain points in different cooling channels.In this figure,the growth of the circumferential residual strain is nonlinear in the initial five cycles.However,the growth rates of residual strains drop quickly until they reach steady states.Inferred by it,the residual strain would be accumulated linearly in the subsequent cycles.This result is consistent with the general evolution law presented in our previous work,31in which a half-channel model was employed.In fact,it is controlled by the mechanical properties of copper alloy,which has been explained in detail in Ref.31.Fig.16 also shows that the discrepancies between the residual strains in different cooling channels increase with the work cycle proceeding,which means that the cooling channels have growth rates of the residual strains different from each other.Since the residual strain differences are enlarged gradually in the subsequent cycles,the circumferential localization effect of the residual strain would be significantly enhanced in reusable thrust chambers.

Fig.16 Residual strain as a function of cycle number.

The quasi static damage caused by the accumulation of residual strains can be predicted by38

where εendis the strain at the end of the considered cycle,εbeginis the strain at the beginning of the considered cycle,and εuis the ultimate strain of the considered material.According to Eq.(11),the quasi static damage accumulated in the considered cycle would remain constant as the work cycle proceeds.Although the residual strains in the subsequent cycles have not been presented in Fig.16,the quasi static damage could be estimated based on the residual strains during the initial ten cycles.To identify what roles different damages play on the failure of the inner wall,the damages accumulated in each cycle are summarized in Table 2.The low-cycle fatigue damages are predicted using the fatigue test data of NARloy-Z in Ref.39.As shown in Table 2,the low-cycle fatigue damage in each cycle is almost equivalent,while the quasi static damage accumulated in a considered cycle declines.Nonetheless,the accumulation of the quasi static damage seems to be stabilized after ten cycles.Because the quasi static damage is greater than the low-cycle fatigue damage by one order of magnitude,the total damage is dominated by the quasi static damage.It can be noted that the change pattern of the total damage withwork cycles is consistent with that of the quasi static damage.Since the predicted service life is simply a linear extrapolation cycle number from the total damages of the completed cycles,40as a result,the life obtained at the end of a considered cycle rises when the cycle number increases.The life obtained at the end of the first cycle is nearly twice as long as that of the second cycle.However,the predicted lives after ten cycles are likely to tend to be constant.These results demonstrate that the traditional single-cycle life prediction which regards the service life as the reciprocal value of the total damage15is a relatively conservative and safe method for engineering.As discussed above,the failure of the cooling channel in the nearthroat region would occur at the maximum residual strain point.Table 3 presents the predicted damages and service lives at the maximum residual strain points in different cooling channels based on the thermal-structural analysis of ten cycles.The quasi static damage of Channel 3 is apparently greater than those of other channels,while the low-cycle fatigue damage of Channel 3 is much smaller than those of other channels.Ultimately,Channel 3 has a much shorter life than those of other channels,which once again demonstrates that the service life is controlled by the quasi static damage resulting from the thermal–mechanical ratcheting.The maximum discrepancy of the predicted lives between different cooling channels is close to 30%.The data indicates that the damage localization effect is so noticeable that much attention should be paid to it in the design phase of thermal protection systems of thrust chambers.For a reusable thrust chamber taking account of both performance and safety,the life prediction in this paper based on the results of multi-cycle thermal-structural analysis with a multichannel model is expected to capture the damage localization effect and track its evolution.

Table 2 Predicted damages and service lives at the maximum residual strain point.

Table 3 Predicted damages and service lives of different cooling channels.

4.Conclusions

(1)The fluid-thermal coupling calculation in this paper indicates that the chamber wall near the throat region operates in significantly elevated heat fluxes.Owing to the effects of transcritical mixing and combustion processes,the heat loads of the thrust chamber wall are apparently non-uniform in the circumferential direction.

(2)The nonlinear thermal-structural analysis with a multichannel model in this paper reveals that there are noticeable disparities between different cooling channels in terms of temperature and strain distributions at the end of the hot run phase.Hence,the cooling channels own different temperature ranges,strain ranges,and residual strains.Circumferential non-uniformity of heat flux should be responsible for the deformation localization effect.

(3)The residual strains discrepancies between different cooling channels are enlarged gradually as the work cycle proceeds,and the circumferential localization effect of the residual strain would be significantly enhanced in reusable thrust chambers under cyclic operation.

(4)The post-processing damage analysis suggests that the low-cycle fatigue damage accumulated in each cycle is almost unchanged,while the quasi static damage accumulated in a considered cycle declines.Nonetheless,the growth rate of the quasi static damage seems to be stabilized after several cycles.The service life of the chamber wall is dominated by the quasi static damage.(5)The maximum differences of the predicted lives between different cooling channels is close to 30%.The damage localization effect cannot be ignored in the design phase of reusable thrust chambers.The damage analysis in this paper based on the results of multi-cycle thermalstructural analysis with a multi-channel model could comprehensively consider the effect.