Anti-disturbance attitude control of combined spacecraft with enhanced control allocation scheme

Jianzhong QIAO,Zhibing LIU,Wenshuo LI

School of Automation Science and Electrical Engineering,Beihang University,Beijing 100083,China

KEYWORDS

Abstract In this paper,we propose a novel anti-disturbance attitude control law for combined spacecraft with an improved closed-loop control allocation scheme.More specifically,a saturated approach is adopted to guarantee the global asymptotic stability under control input saturation.To enhance the robustness of the system,a nonlinear disturbance observer is constructed to compensate the disturbances caused by inertial parameter uncertainty and unmodeled dynamics.Next,the quadratic programming algorithm is used to obtain an optimal open-loop control allocation scheme,where both energy consumption and actuator saturation have been considered in the allocation of the virtual control command.Then,a modified closed-loop control allocation scheme is proposed to reduce the allocation error under the actuator uncertainty.Finally,stability analysis of the closed-loop system with the proposed allocation scheme is provided.Simulation results confirm the effectiveness of the proposed control scheme.

1.Introduction

Combined spacecraft refers to a class of cooperative or noncooperative target spacecraft that are combined together to accomplish certain space tasks such as space operation and space debris clearance.Combined spacecraft is gaining popularity due to its potential capacity in space missions that are beyond the capability of a single spacecraft.As one of the key technologies for combined spacecraft systems,highprecision and reliable attitude control has attracted increasing attentions among researchers throughout the world.For orbiting combined spacecraft,the attitude dynamics are strongly nonlinear and vulnerable to multiple sources of disturbances,including external disturbances,parametric uncertainties and modeling errors.Up to now,considerable results have been published on attitude stabilization control of the combined spacecraft.However,most of the existing results have not taken the actuator constraints into account,which may lead to actuator saturation and cause serious discrepancies between the expected and actual control signals.Moreover,an assembled spacecraft control system is over-actuated with redundant actuators.Therefore,it is important to study the problem of how to properly allocate the control command among the actuators.A major challenge in the control allocation problem is how to deal with the uncertainties caused by the misalignment of actuators and the measurement error of torque magnitudes.The difficulties mentioned above have significantly complicated the design of combined spacecraft attitude control system,especially when all these aforementioned issues are considered simultaneously.

Accounting for constraints such as input saturation in the controller design has been the focus of tremendous research efforts over the past decade(see Refs.1–10and references therein).Several inspiring and effective approaches,such as variable structure control,adaptive control and optimal control,have been developed to address the identified challenges.Specifically,a saturation control scheme has been proposed in Ref.11for an under-actuated rigid spacecraft,where a nonstandard representation of the attitude,allowing the general motion to be decomposed into two rotations,is adopted to facilitate the derivation of control law.An attitude stabilization scheme has been developed by Wallsgrove and Akella in Ref.12,where hyperbolic tangent functions are incorporated to guarantee a smooth control input.With the controller designed in Ref.12,we can adjust the sharpness of the control input by tuning a set of parameters,thus to a large extent avoiding the chattering phenomenon which is widely recognized as a critical disadvantage of the variable-structure method.A nonlinear bounded control has been developed in Ref.13by employing the back-stepping procedure and an inverse tangent-based tracking function.Due to its simplicity and effectiveness,the Proportional-Derivative(PD)or PD-like control methods have also been extensively investigated.Incorporating a standard hyper-tangent function,a simple saturated PD control scheme has been developed in Ref.14,where it is guaranteed that the attitude of rigid spacecraft is asymptotically stable regardless of the initial condition.As we all know,multiple sources of disturbances widely exist in spacecraft systems and will cause performance degradation or even instability of the control system.

The above mentioned control approaches,however,have not explicitly taken disturbance rejection into consideration.Popular approaches to anti-disturbance control include disturbance attenuation and disturbance compensation.The former is to design a feedback control law in order to reduce the effect of disturbances to a certain degree,while the latter constructs an observer to derive a disturbance estimate which is then used for feed-forward compensation.Among the disturbance compensation methods,a novel Nonlinear Disturbance Observer Based Control(NDOBC)method has been proposed in Ref.15for robotic manipulators and in Ref.16for missile control.The disturbance estimation error was guaranteed to converge to zero asymptotically under the condition that the disturbance varies slowly.A novel composite controller has been proposed in Ref.17to deal with multiple disturbances,where the DOB is used in the inner loop for disturbance compensation and the H∞controller is adopted in the outer loop to attenuate the effect remaining disturbances as well as disturbance estimation errors.The disturbance observer based composite intelligent learning control scheme has been proposed in Refs.18,19and shown to achieve enhanced performance in the presence of unknown nonlinearity.In Refs.20,21,the disturbance observer based approach has been combined with the game theoretical approach to achieve optimal performance.

The combination of multiple spacecraft has inevitably introduced more control effectors than what is actually required,which makes the combined spacecraft an overactuated system.It is known that the performance of an over-actuated system can be improved if the actuator redundancy is properly exploited.The control allocation(CA)technique is a common method to deal with the problem of control redundancy,where the command signals generated by the baseline controller are allocated to different actuators in order to meet the requirement of controller design.The existence of redundant actuators will certainly provide extra flexibility to the design of control system.An increase in the number of redundant control effectors,however,will lead to a more complicated design of control system.The issue control allocation is especially important when the actuator fails or when the control surface is damaged.In such cases,it is required that the control commands be reallocated among the remaining healthy control actuators to maintain an acceptable performance.Control allocation problem has been intensively studied in the past decades,with typical solutions including daisy chaining,22direct allocation,23,24linear or nonlinear programming-based optimization,23and dynamic control allocation.24–26In Ref.27,a pseudo-inverse method has been proposed,and a fixed-point based algorithm has been implemented and tested in a benchmark spacecraft model.In Ref.28,a mini-max control allocation scheme is developed to meet the multiple conflicting objectives simultaneously by finding a ‘Pareto’optimal solution.In Ref.29,a control scheme has been proposed,where the real-time structure is fed back and the structural load constraints are taken into consideration in the design of control allocation scheme.In Ref.30,constrained optimization based control allocation scheme has been employed to achieve desired torque without violating the specified constraints on monitored load points.The method proposed in Ref.30adopts the dynamic control allocation approach,where the resulting allocation scheme also depends on the allocation of the previous sampling instant.This method penalizes the actuator rates and can therefore be seen as an extension of the regular quadratic programming based allocation scheme.In Ref.31,a novel robust control allocation approach has been developed in the presence of partial or complete loss of control effects.Most of the above mentioned control allocation schemes,though successfully applied to certain tasks,are all open-loop schemes which have not fully exploited the real-time information.Among the few studies on the closed-loop allocation scheme,a detailed comparison has been made in Ref.32between open-loop and closed-loop performance for sixteen control allocation schemes.However,in Ref.32,stability issues have not been considered for the closed-loop system when the control allocation scheme is combined with the baseline controller.Having recognized this,Zhang and Chen proposed a closed-loop control allocation scheme in Ref.33based on the cascaded generalized inverse method,and provided sufficient and necessary conditions for the satellite system to be stable.In Ref.34,a novel saturated PD control law incorporated with Closed-Loop Control Allocation(CLCA)has been proposed by Hu and Li with guaranteed asymptotic stability of the closed-loop system.

In this paper,a novel control scheme,which combines the DisturBance Observer based Saturated Attitude Control law(SAC+DOBC)and a Modified Closed Loop Control Allocation(MCLCA)approach,is developed for attitude stabilization of the combined spacecraft.Specifically,the SAC+DOBC control law is designed to generate a virtual control command,which can ensure the attitude stability in the presence of disturbance and control input constraints.A modified closed loop control allocation scheme is used to allocate the virtual control command to each individual actuator with minimum allocation error on the condition of reduced energy consumption and actuator uncertainty.It is noted that the MCLCA method proposed in this paper differs from the conventional CLCA scheme(see Ref.34for details)in that the flow of allocation error signal has been modified to increase the error sensitivity of the control loop,which makes possible a higher convergence rate.Based on Ref.34,we prove,in a more rigorous manner,that the modified closed-loop control allocation system is stable.The contributions of this paper include:(A)the disturbance observer based saturated attitude control law is proposed to endow the attitude control system with enhanced robustness against disturbances,and(B)a modified closed loop control allocation scheme is developed to reduce allocation error in the presence of actuator misalignment.

This paper is organized as follows:Section 2 presents the combined spacecraft model and control problem formulation.The attitude control law combining a saturated method with DOBC is presented in Section 3.The modified closed-loop control allocation design and stability proof are shown in Section 4.Simulation results are provided to verify the theoretical results in Section 5.Finally,conclusions and future work are stated in Section 6.

2.Combined spacecraft modeling and problem statement

In this section,the dynamic model of the combined spacecraft is presented and the attitude control problem is formulated.

2.1.System setup

For a combined spacecraft,the combination of multiple objects will introduce strong nonlinearities into the attitude dynamics.In addition,the parameter uncertainty,such as the unknown inertia matrix,will severely affect the precision of attitude control.In order to simplify the modeling work of the combined spacecraft,the following assumptions are made:

Assumption 1.The tangential force between two objects is big enough to guarantee that relative attitude of the objects keeps stable when rotating rapidly.

Assumption 2.The combined object can be regarded as a rigid body and the issues like elastic vibration and shape variation resulting from mutual collision can be ignored.

Under the assumptions made above,attitude dynamics of the combined spacecraft with Euler parameters are given as follows35:

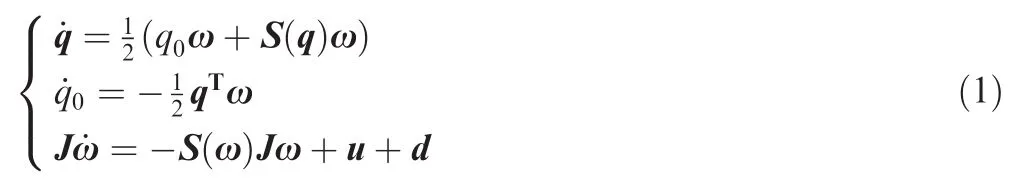
where q（t）and q0（t）are the vector element and the scalar element of the attitude quaternion respectively;ω（t）is the angular velocity vector with respect to the inertial frame;J is the inertia matrix of the combined spacecraft;u（t）is the control inputs;d represents the lumped disturbance consisting of inertia uncertainty and unmodeled dynamics;S（·）denotes a skewsymmetric matrix given by

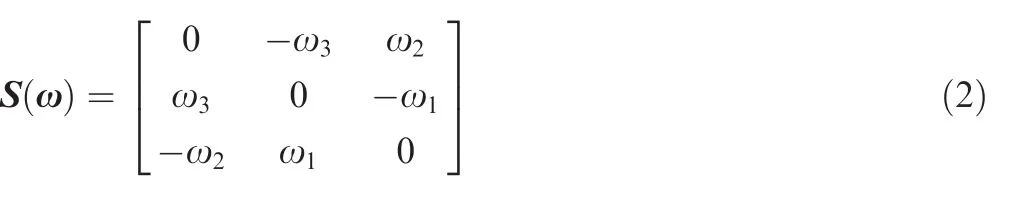
The control signals are constrained by a common maximum magnitude,that is,

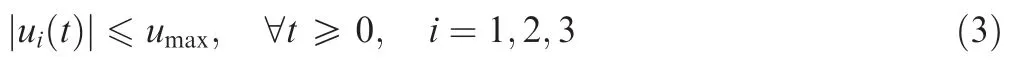
It is assumed that the disturbances vary slowly and are strictly dominated by the control signal,that is,

This assumption is quite common in practice and can also be found in Refs.15,16In fact,the first line in Eq.(4)makes sense because the uncertain environment should be taken into account in the design of the actuator,and the second line in Eq.(4)stems from the fact that it is easy to attenuate the high-frequency disturbance with a low-pass filter,and thus it is only the low-frequency,i.e.,slowly-varying,disturbances that will affect the control performance.For simplicity,dmaxand umaxare taken to be constants in the present formulations.Typically,there is a separate bound,umax（i）,for each component ui, but a common saturation constraintadopted here,which may be conservative but can help to streamline the analysis.

2.2.Control objective

Considering the spacecraft attitude control system given by Eq.(1)under the preceding reasonable assumptions,the objective of attitude control is to design u subjected to Eq.(3)such that,for all the physically realizable initial conditions,global asymptotic stability of the attitude control system is guaranteed,which can be expressed as

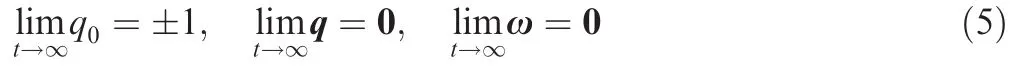
3.Composite controller design

To address the attitude control problem of the combined spacecraft,this paper borrows the idea of Refs.23,34where the baseline controller and the control allocation are designed independently.The structure of the closed-loop system with control allocation has been shown in Fig.1.Our control scheme consists of:(A)a virtual control law which specifies the total control effort to be produced,and(B)a control allocation scheme which maps the total control demand onto the individual effectors.Since the control law and the allocation scheme are designed independently,the controller can be reconfigured easily when the effectiveness of the actuators changes over time,and the control law does not have to be redesigned in the event of an actuator failure.Furthermore,the actuator uncertainty can also be taken into account.

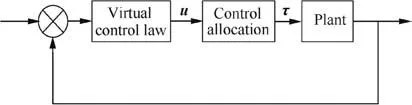
Fig.1 Control configuration when control allocation is used.

3.1.Saturated globally stabilizing control law design

First,let us consider the case where d=0.We assume that the attitude and angular velocity are both measurable for feedback.Inspired by Ref.12,a control law that satisfies Eq.(3)can be provided by the sum of a proportional attitude feedback term and a smooth switch-like mixed feedback term as follow:

where Tanh（·）denotes the hyperbolic function that is defined as

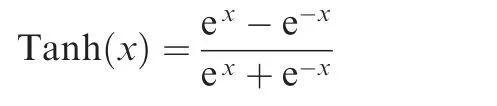
and the parameter β is selected to satisfy

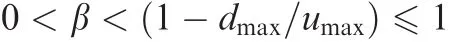
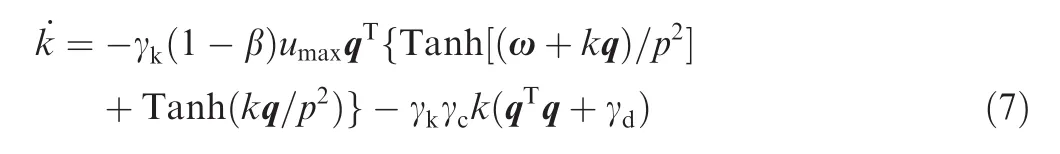
where k（0）=k0is an arbitrary scalar,γkand γdare both positive scalars,and γcis a scaling/conversion factor that allows consistent physically meaningful units.In Eqs.(6)and(7),p2is a nonzero constant scalar that governs the magnitude of the control rates.For detailed roles of k，p2，β and the stability proof,readers can refer to Ref.12.

The saturation limit is not difficult to guarantee since the Euler parameters and hyperbolic tangent functions are both bounded in nature(i.e.,|qi|≤ 1 and|tanh（·）|≤ 1):

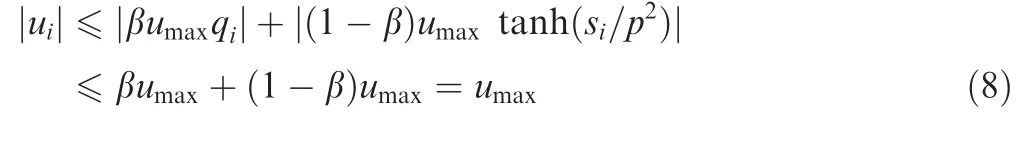
3.2.Composite controller design based on disturbance observer

The control law proposed above is effective only for the case when there is no disturbance,while in practice,the combination of multiple objects may lead to big uncertainty of inertial parameter and unmodeled dynamics.So in this part we will focus on designing a composite controller based on the nonlinear disturbance observer to compensate the disturbances.

Inspired by the ideas of Chen et al.15and Chen,16one can design a nonlinear disturbance observer to estimate the disturbances in Eq.(1)in the following way:

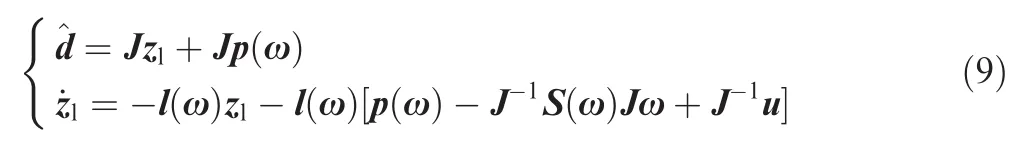
In this paper,p（x）is chosen as

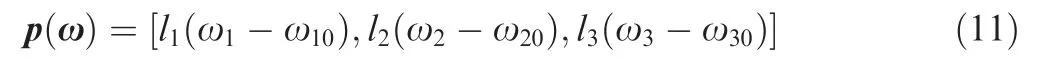
in which li＞ 0 （i=1，2，3） are positive constants,and ω10，ω20，ω30are the initial values of the angular velocity in each tunnel.Then the matrix l（ω）is

In the middle of the fields the parson24 met them, and when he saw the procession he said, For shame, you good-for-nothing girls, why are you running across the fields after this young man? is that seemly? At the same time he seized the youngest by the hand in order to pull her away, but as soon as he touched her he likewise stuck fast, and was himself obliged to run behind.

Remark.It should be noted that in the engineering practice,the spacecraft being controlled does not always start from the steady state.Therefore,the initial values of the angular velocity have been included in p（ω）to address this.Similar choices have also been adopted in Refs.15,16.

Define the estimate error as

Under the assumption in Eq.(4),combining Eqs.(1),(9),(10)and(11),one can get

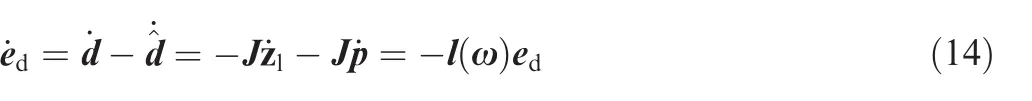
It can be derived from Eq.(14)thatconverges to d at an exponential rate if l（ω）is chosen such that Eq.(14)is globally exponentially stable.

After the disturbance is estimated by the observer in Eq.(9),d in Eq.(1)can be replaced byto design a composite controller where the control saturation and disturbances are simultaneously addressed.The composite controller is given as follows:

From Eq.(15),one can easily obtain

4.Optimal control allocation design

Although the attitude stability is guaranteed under the disturbances and control input constraint,it should be noted that other practical issues,such as energy consumption,actuator misalignments,actuator saturation,and rate saturation,should also be taken into consideration in the control system design.For an over-actuated system like the combined spacecraft,it is useful and convenient to deal with the actuator uncertainty by controlling re-allocation.28

Considering the actuator amplitude and T rate constraints,it is reasonable to give an overall actuator limit as follows:

where

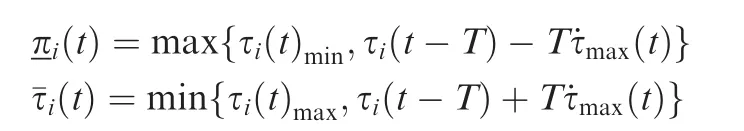
and τmax, τminare the upper and lower bounds on actuator amplitude,˙τmaxis the maximum admissible actuator rate,and is the sampling period.

In view of actuator misalignment error,we denote

Following Refs.23,34,the control allocation scheme can be developed in the following way:First,optimize the objective function,construct the open-loop constrained optimal control allocation scheme to allocate the control commands,and then give the closed-loop control allocation scheme by minimizing the allocation error caused by the actuator uncertainty.

4.1.Open-loop constrained optimal control allocation design

The dynamic control allocation method that we propose can be formulated as a sequential quadratic-programming problem:

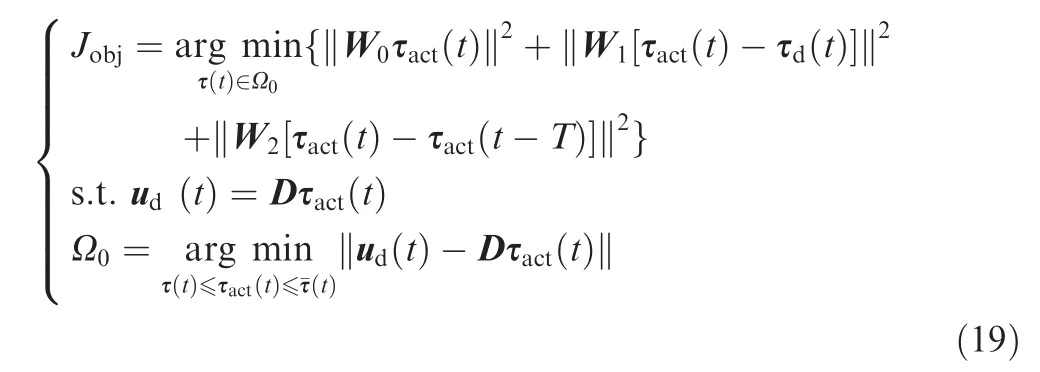
where W0,W1and W2are relevant diagonal positive weighting matrices,ud（t）and τd（t）are the desired system control torques and actuator torques respectively,and uact（t）and τact（t）are the actual system control torques and actuator torques respectively.The selections of the matrices Wi（i=0，1，2）have been elaborated in Refs.31,34.

If we ignore the actuator constraints and misalignments,the optimal control allocation problem in Eq.(20)has the following solution:

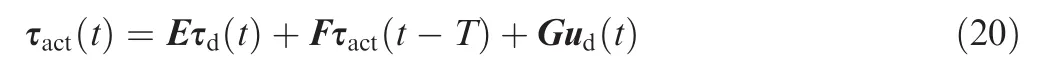
In view of Eq.(20),the actual actuator torque is the weighted sum of the three terms: τd（t）, τact（t-T）and ud（t）.A more detailed proof can be found in Ref.34.

4.2.Closed-loop constrained optimal control allocation design

Ideally,when there is no actuator constraint or misalignment error,Eq.(20)becomes an explicit solution of the optimization problem(19),that is,ud（t）=Dτact（t）.However,due to the presence of actuator uncertainty,only a least square solution can be provided,which means that the allocation errorwill affect the overall control system.

In this subsection,actuator constraints are taken into account though a control input limit has already been considered in Eq.(16).To make the synthesized torques τact（t）and the desired torques τd（t）within a pre-specified interval,two diagonal positive gain matrices R0and R1are introduced as

where r0and r1are selected according to the following rules:

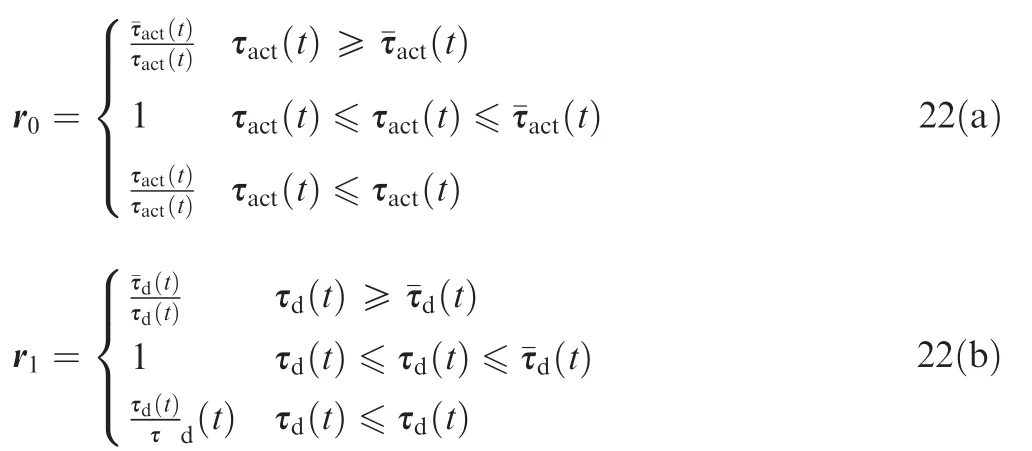
Accordingly,the optimal quadratic programming problem formulated in Eq.(19)becomes

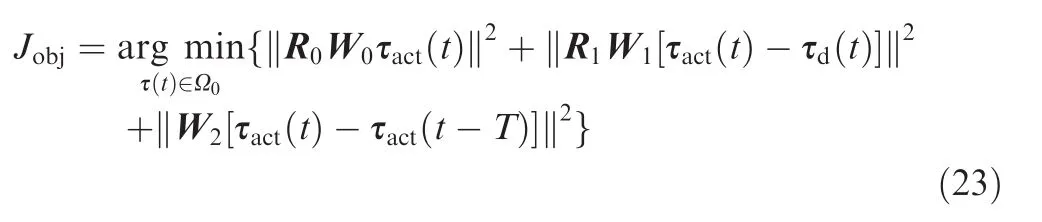
which has the following solution:

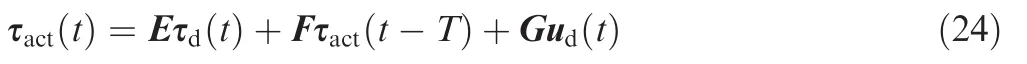
Fig.2 Modified closed-loop control allocation scheme.

To guarantee that uact（t）converges to ud（t）,a novel control allocation scheme,namely the modified closed-loop control allocation scheme,is proposed in this subsection.Borrowing the idea of feedback control,Hu and Li proposed a feedback control allocation scheme(see Ref.34for more details)to guarantee that uact（t）approached to ud（t）asymptotically and achieved great improvement in the allocation performance.However,as will be shown below,there is still huge space to minimize the allocation error.The modified closed-loop control allocation scheme has been presented in Fig.2,in which z-1is a delay or discretization operator.

Remark.It should be noted that the proposed closed-loop feedback scheme is quite different from the CLCA scheme proposed in Ref.34As shown in Fig.2,the dash dot line denotes the CLCA scheme,which means that the allocation error is only fed back to the terms E and F,and does not affect the term G.Actually,in most cases,G is a weighting part of the composition τact（t）compared to term E and F.Therefore,a modified loop structure is proposed,which is shown by the solid line in Fig.3.This scheme can achieve more effective error reduction since the influence of the allocation error is shared by all the three terms.

We are now in a position to show how to guarantee the stability of the closed-loop control allocation system by properly designing the system parameters.The main results are stated in the following theorem:

Theorem.For the combined spacecraft systems,the stability of the closed-loop control allocation system(shown in Fig.3)can be guaranteed if the allocation parameters are selected such that the characteristic equation of the system satisfies

Proof.To analyze the closed-loop system,the actuator torques can be described by the following discrete-time model:

where

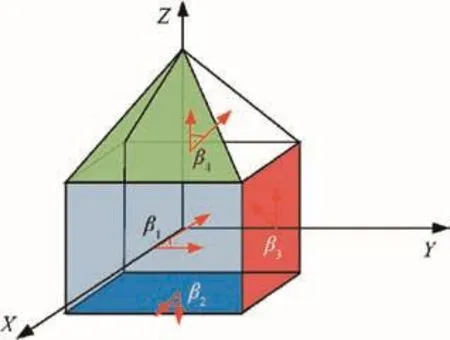
Fig.3 Combined spacecraft mode.

From Eqs.(24)and(25),one can obtain

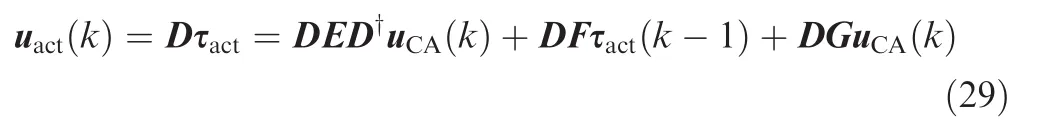
and further get

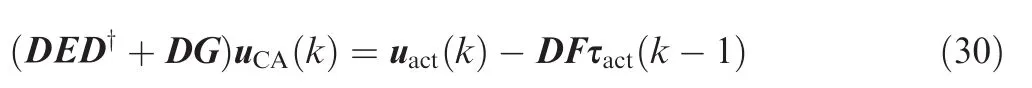
Then,by defining M=DED†+DG,Eq.(27)becomes

Multiplying M by Eq.(25),one can obtain

Combining Eq.(28)with Eq.(29),we have

Then,we transform Eq.(30)into a discrete-time model using the standard Z-transformation:

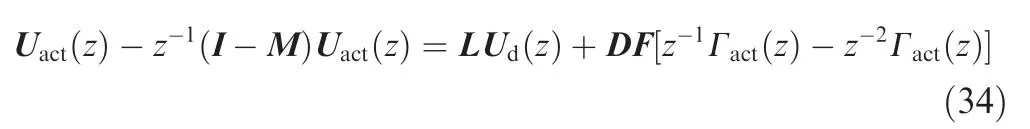
That is

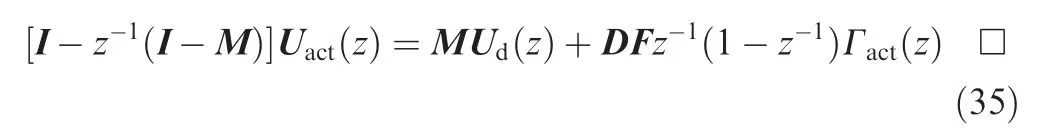
Now we introduce the following lemma which will be used for our stability analysis:

Lemma 1(Ref.36).For a matrix A ∈ Rn×nand a unit matrix I∈ Rn×n,the eigenvalues of A and I satisfy

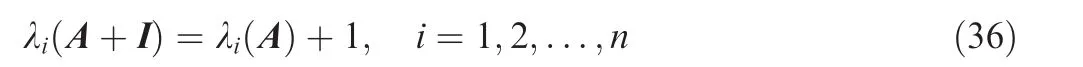
where λi（*）（i=1，2，...，n）denote the eigenvalues of a given matrix.

The characteristic equation of the closed-loop control allocation system from Eq.(25)can be obtained from8,34

which is

For a discrete-time system,the necessary and sufficient condition to stability is that the norms of all the characteristic roots are smaller than one.

The eigenvalues of the characteristic equation of the closedloop control allocation system can be calculated as follows:

where L=DED†.Referring to Refs.31,32,through a singular value decomposition of D and DW-1,one can easily conclude that the eigenvalues of L satisfy

Based on Lemma 1,it is obvious that

and further we have

From Eqs.(25)and(39),the norms of all the characteristic roots are smaller than one,which means that the system(25)is asymptotically stable.

5.Simulation and analysis

In order to verify the effectiveness and performance of the proposed composite controller and the modified closed-loop control allocation scheme,numerical simulations have been carried out using the MATLAB/Simulink platform.The model commonly used for combined spacecraft systems is shown in Fig.4,which has been adopted for our performance verification.The combined spacecraft system under consideration is composed of a square and a triangular shape craft,with four jet nozzles installed on it as actuators.To make the simulation more convincing,we calculate the simulation parameters like the inertial matrix from the model.In normal circumstances,three of the jets are used to generate thrust along with coordinate axis to drive attitude towards stability,and the fourth one is installed with inclined direction on the triangular craft to cooperate with the other three jets.

However,in practice,some alignment errors such as the jets’position and direction deviation will always exist due to the limited manufacturing precision.In this paper,it is assumed that the jets are tilted over nominal direction with constant angles Δβi（i=1，2，3，4）,and a constant distant ΔRi（i=1，2，3，4）is used to model the position uncertainty.Then the control signals with actuator misalignment can be expressed as

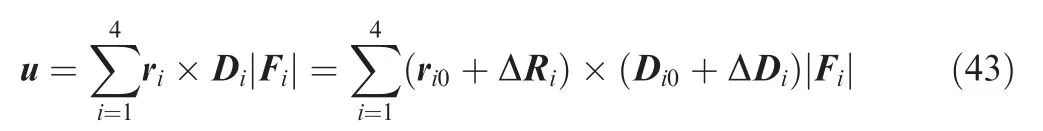
where

and

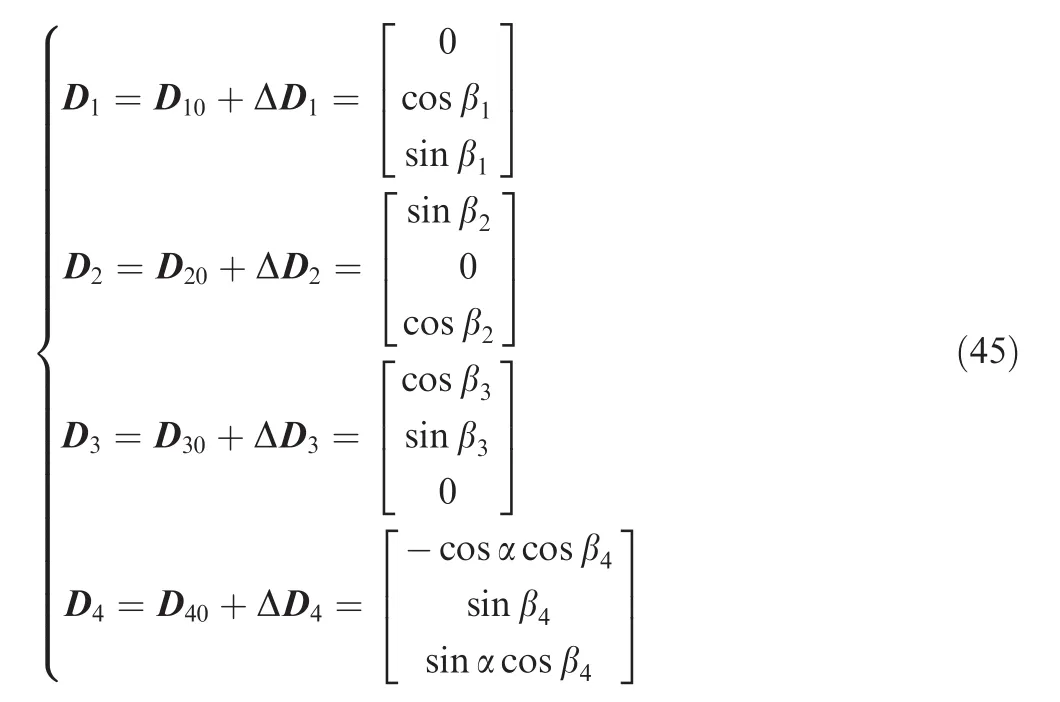
where α is the slant angle of the triangle.Generally,the misalignment angle errors are very small in practice.We therefore adopt approximation methods to simplify Eq.(45),that is,let sinβi= βiand cosβi=1.Then the virtual signals mapped to actuators are expressed as

where

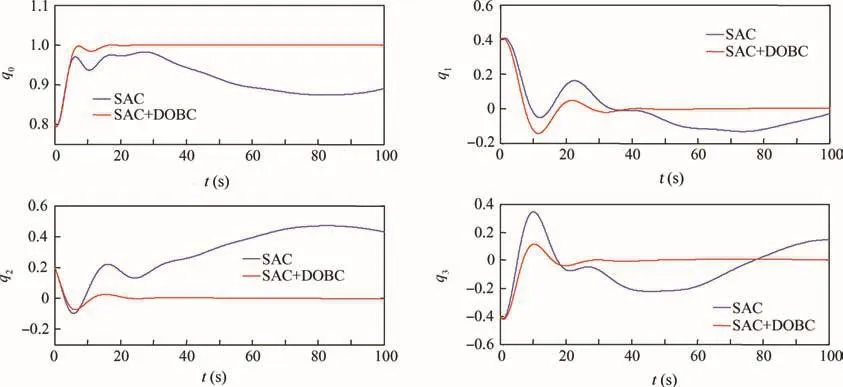
Fig.4 Time responses of attitude quaternion vector.

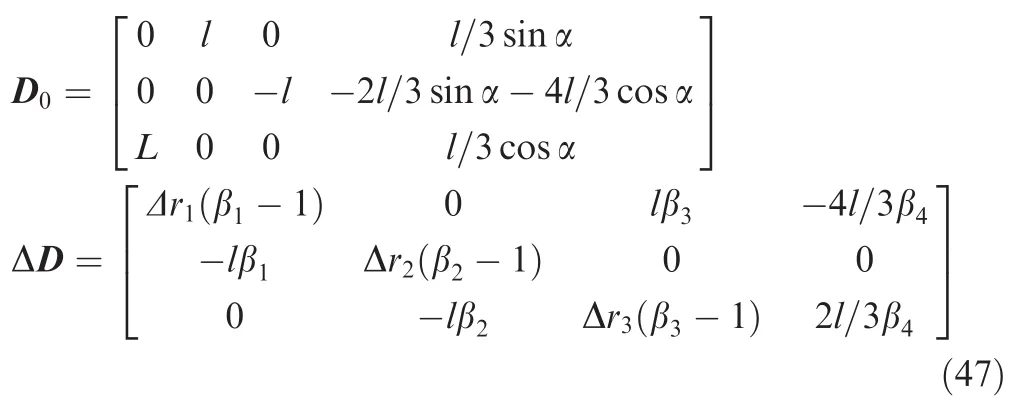
and ΔD denotes the joint effect of actuator misalignment and direction error.Other parameters used in the simulation are listed in Tables 1 and 2,and the disturbances consisting of inertial uncertainty and unmodeled dynamics are given by

The simulation works are completed in two steps:The first step is to verify the effectiveness of the composite controller under disturbances,and the next step is to verify the modified control allocation under the actuator misalignment and constraints.

Step 1.Attitude control with disturbances.In this simulation case,the SAC method in Ref.12is first presented as a comparison.Further,the composite anti-disturbance controller is applied with the same condition.Figs.4 and 5 show the time responses of the attitude quaternion vector and angular velocities under disturbances respectively.As shown in the figures,it is a sharp contrast that the composite controller achieves a more perfect performance while the SAD controller loses ef ficacy under the disturbances.With the composite controller,the spacecraft attitude quaternion qi（i=1，2，3）converge to 0 and scalar q0converge to 1 smoothly within 30 s while vibrate drastically with the SAD method under disturbances.Correspondingly,the spacecraft angular velocities converge to zero smoothly within 30 s with composite controller whilevibrate drastically with the SAD method under disturbances.Though a steady-state error less than 10-3rad/s exit because of the disturbances,it can satisfy most precision needs of the stability control.

Table 1 Main parameters of a combined spacecraft.

Table 2 Parameters used in simulations.

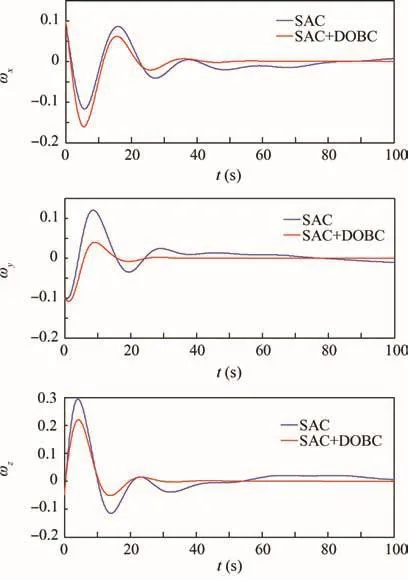
Fig.5 Time responses of angular velocities.

Fig.6 Disturbance and its estimation.

Fig.7 Disturbance estimate error.

The actual disturbances and its estimation by the disturbance observer are shown in Fig.6,and the estimate error is presented in Fig.7.It can be seen that even though there exists the estimation error,the estimated values can follow the actual disturbances within a short period of time.The estimation error results from the assumption that˙d≈0 while the actual disturbance rate˙dact≠0.This error will further cause steadystate error in attitudes and angular velocities.If a constant disturbance is added on the model,the composite controller will have more perfect performance.

The time responses of virtual signals under the composite controller have been shown in Fig.8.Obviously,the virtual control signals do not exceed the magnitude limit 2N·m.It should be noted that in order to compensate the effects of disturbances,the control inputs do not converge to zero even after the attitudes have converged to zero.

Fig.8 Control input signals.

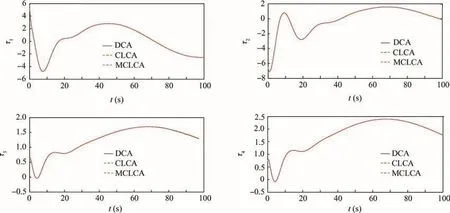
Fig.9 Time responses of actuators.

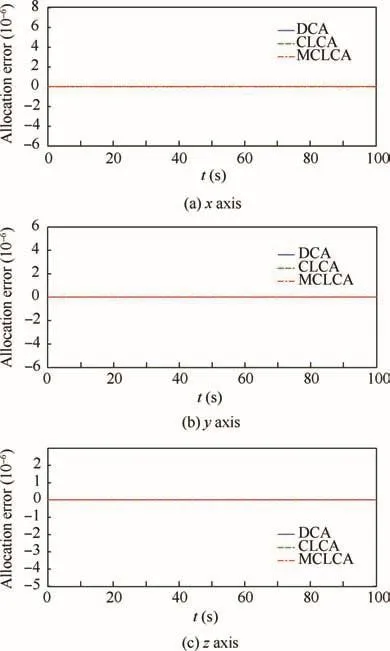
Fig.10 Allocation errors without actuator uncertainty.

Step 2.Modified optimal control allocation with actuator misalignment and saturation.Based on the virtual control commands synthesized by the composite controller under the disturbances in the last step,modified closed loop control allocation(MCLCA)scheme is verified in this step.The method proposed in Refs.30,34named DCA and CLCA is applied for comparison purpose.Fig.9 shows the time responses of the actuators without considering the actuator uncertainty.It can be seen that the three methods reach the same good performance under the same condition.This is not surprising because when there is no actuator uncertainty present,all three methods are optimal solutions to the problem under consideration.The allocation errors are shown in Fig.10,which further confirms that the three methods are equally effective when the actuator is uncertainty free.

Fig.11 Time responses of actuators.

Fig.12 Allocation errors.

The time responses of the actuators in the presence of actuator uncertainty have been presented in Fig.11.The control allocation errors have been presented in Fig.12.Obviously,the MCLCA scheme achieves a more desirable performance compared to the other two methods.Attitude stabilization can also be guaranteed by this effective control allocation scheme.The control allocation errors are negligible and will not violate the properties of the SAC+DOBC method.In addition,this control scheme is as energy-efficient as the CLCA method,which is a favorable feature for the spacecraft attitude control system.

6.Conclusions

In this paper,an anti-disturbance saturated control method incorporated with a modified closed-loop control allocation scheme has been proposed for attitude control of combined spacecraft.The disturbance observer based saturated control law is firstly proposed to achieve attitude stabilization in the presence of disturbances and control input constraints.Then,the modified closed-loop control allocation approach is derived to reduce the allocation error caused by the actuator uncertainty.Numerical simulations for the proposed schemes are presented to demonstrate the superiority of the proposed scheme compared to the existing methods.In the future research,theoretical analysis from the perspective of stability margin should be carried out to further demonstrate the advantages of this allocation scheme.

Acknowledgements

This study was co-supported by the National Natural Science Foundation of China(Nos.61627810,61320106010,61633003,61661136007,61603021),the Program for Changjiang Scholars and Innovative Research Team(No.IRT_16R03),and Innovative Research Team of National Natural Science Foundation of China(No.61421063).

Appendix A.Supplementary data

Supplementary data associated with this article can be found,in the online version,at https://doi.org/10.1016/j.cja.2018.06.009.