Multi-scale strength analysis of bolted connections used in integral thermal protection system

Heng LIANG ,Yuqing WANG ,Mingo TONG ,*,Junhu ZHANG

a College of Aerospace Engineering,Ministerial Key Discipline Laboratory of Advanced Design Technology of Aircraft,Nanjing University of Aeronautics&Astronautics,Nanjing 210016,China

b Shanghai Aircraft Design and Research Institute,Shanghai 201210,China

KEYWORDS

Abstract Efficient and accurate strength analysis of bolted connections is essential in analyzing the integral thermal protection system(ITPS)of hypersonic vehicles,since the system bears severe loads and structural failures usually occur at the connections.Investigations of composite mechanical properties used in ITPS are still in progress as the architecture of the composites is complex.A new method is proposed in this paper for strength analysis of bolted connections by investigating the elastic behavior and failure strength of three-dimensional C/C orthogonal composites used in ITPS.In this method a multi-scale finite element method incorporating the global–local method is established to ensure high efficiency in macro-scale and precision in meso-scale in analysis.Simulation results reveal that predictions of material properties show reasonable accuracy compared with test results.And the multi-scale method can analyze the strength of connections efficiently and accurately.

1.Introduction

Thermal Protection System(TPS)is a key structure of hypersonic vehicles to keep the temperature of internal structure in a certain range and ensure safety of the vehicles in the elevated temperature environment.Conventional TPS is incapable of bearing external loads and costly in maintenance due to its poor mechanic properties.With the increasing demand for structural efficiency,a new concept of TPS called‘integral thermal protection system(ITPS)’was proposed.1–3ITPS has the function of thermal insulation and the capability to withstand aerodynamic and structural loads;besides,it is reusable and can reduce the overall weight of hypersonic vehicles.

The materials of ITPS are mainly C/C and C/SiC because of their high specific strength,high specific stiffness and excellent ablation resistance.However,there is a contradiction in ITPS:the material with strong bearing capacity usually has good thermal conductivity,which is not conducive to structural thermal protection,while lightweight insulation material is low in bearing capacity.To find suitable materials,an enormous number of research including experiments and numerical simulations is needed.In numerical simulations,the Finite Element(FE)method is mainly considered,thanks to its efficiency and economy,to shorten development cycle and reduce research risk.

The strength of bolted connections in ITPS is a main concern because failures usually occur at the connections.The homogenization method,which uses macroscopic homogenized properties of composites to characterize the structure,is widely used in bolted connection strength analysis.Egan et al.4used the nonlinear finite element code to model the single-lap joints with countersunk fasteners,and analyzed the stress distribution at the countersunk hole boundary.The results showed that the finally compressive through-thickness stresses are presented at the damageable region of the countersunk hole,and increase with bolt-hole clearance.Li et al.5calculated the nonlinear stress distribution of C/SiC joints with pins or bolts and investigated the influences of hole parameters on the mechanical properties of C/SiC substrates.The simulation results were consistent with the experimental fracture loads and damage modes.Tang et al.6used the Hashin’s theory as the damage initiation criteria to study the mechanical property and failure mechanism of Carbon–Carbon braided composites(C–Cs)bolted joints structure subjected to unidirectional tensile load,the FEM results had a good agreement with the test values.Du et al.7investigated failure behavior of Pultruded Fiber Reinforced Polymer(PFRP)bolted joints and proposed a Progressive Damage Analysis(PDA)material model integrating nonlinear shear response,Hashin-type failure criteria and strain-based continuous degradation rules.Hu et al.8proposed an explicit finite element analysis to model progressive failure of bolted composite joints under high bearing strains,the results of which showed the errors could be acceptable if very fine mesh is employed around the bolted area.All material properties in the above studies were established by experiments or numerical methods based on the macroscopic strength theory.The modeling strategies and numerical approaches did not consider stress localization mechanisms in microscale constituents.Besides,corresponding macroscopic strength theory should be developed independently for different materials.

An alternative method is analyzing the mechanical behavior of bolted composite joints considering the heterogeneous mesostructure at mesoscopic scale based on micromechanics.Lomov et al.9,10proposed a finite element model,called meso-FE,to investigate the mechanical behavior of 3D orthogonal woven composite and 2D woven composite by modeling of meso-scale geometric representations.Tsukrov et al.11developed a meso-scale finite element model to predict cure-induced microcracking of 3D orthogonal woven.The model showed good agreement between areas of high parabolic stress within the orthogonal woven material and actual microcracking observed by micro-CT scans.Dai and Cunningham12developed a full finite element meso model and a mosaic macro model to simulate the elastic and damage progression behavior of the 3D woven composite architecture.Both models predicted the tensile modulus and strength within 20%of the experimentally measured values,and the predicted failure sequence was similar to the experimental observation.Warren et al.13developed a three-dimensional progressive damage meso-FE model to capture the onset and initial propagation of damage within a three-dimensional woven composite in a single-bolt,double-shear joint.The onset of damage and trends seen in the model were found to be in agreement with experimental findings.Although meso-FE is a powerful tool to study the relationship between damage patterns and local stress fields in meso-scale,it is very time consuming to establish and analyze the structure.

Thus,multi-scale method,in which information is shared across two or more different length scales,is an efficient method for heterogeneous composite materials.The method establishes the relationship between macro appearance and meso structure,so it has both advantages of high efficiency in macro-scale and high precision in meso-scale.Feng14and Wang15et al.used multi-scale methods to predict the effective modulus of 3D braided composites.Sˇmilauer et al.16predicted the fracture energy,Gf,and the effective length of the fracture process zone,cf,of two-dimensional triaxially braided composites using the multi-scale method.Mao et al.17presented a multi-scale modeling approach for the progressive failure analysis of carbon- fiber-reinforced woven composite materials.Kwon and Park18developed a generalpurpose micromechanics model for the multi-scale analysis of composite structures.Li et al.19proposed a new stressbased multi-scale failure criterion based on a series of offaxis tension tests,and determined their corresponding fiber failure modes and matrix failure modes.Zhang et al.20presented a mechanics based multiscale computational model to predict the deformation,damage and failure response of Hybrid 3D Textile Composites(H3DTCs)subjected to three-point bending.Nerilli and Vairo21developed a nonlinear multi-scale finite-element computational approach to analyze the pin-induced progressive damage of fiberreinforced laminates employed in composite bolted joints.The results showed a good agreement with experimental evidence.However,most of the publications were concentrated on studying material properties using the multi-scale method.There were a few investigations focusing on multi-scale strength analysis of bolted connections.

In this work,a multi-scale method was established to investigate the strength of bolted connections used in ITPS.The method was mainly based on Asymptotic Expansion Homogenization (AEH)method incorporating the global–local method.The AEH method,which is used to decompose a function into global and local components,offers a base tool for this modeling strategy.Bensoussan et al.22detailed the method as the application of mathematical expansion to describe the macroscopic behavior of a system from the description of structure at micro-scale.Many investigations of composite materials with 3D structures were presented by AEH method.14,15,23–26The homogenized solution from the AEH method can be used in a macro-scale analysis,and additionally the AEH method also allows determination of the meso-scale state from point conditions in a macro-scale analysis.The global–local method,based on Saint Venant’s principle,was used to reduce the modeling and computational complexity with reasonable accuracy,27–30as there were hundreds of bolted connections in ITPS.A global model was established with coarse mesh.The stress fields of global model were analyzed approximately with homogenized material properties.According to the stress results of the global model,the most highly loaded region was selected and modeled with refined mesh.The progressive failure analysis was applied for the most critical region by AEH method.Based on this method,the analysis has both advantages of high efficiency in macro-scale and high precision in meso-scale.

The sections are arranged as follows:Section 2 develops and explains the methods for the homogenization applied hereinafter and the failure criteria.A detailed analysis process and calculation codes are developed.The simulation results and comparison with results of material testing are presented in Section 3.Section 4 uses the multi-scale method to analyze the strength of the bolted connections in ITPS.

2.Methods

2.1.Asymptotic homogenization

C/C composite structures have different characteristics in two spatial scales,namely the heterogeneous mesostructure in mesoscopic scale and the homogeneous macrostructure in macroscopic scale.The AEH method is generally employed to correlate the two scales.The Repeating Unit Cell(RUC)of composite structure is the smallest unit in mesoscopic that can be repeated to form a macrostructure.The RUC is assumed to be much smaller than the macrostructure.The length-scale used in RUC is y,while that used in macrostructure is x.Both scales are correlated by a scale parameter ε:

When ε approaches zero,the heterogeneous mesostructure can be regarded as a homogeneous macrostructure,as shown in Fig.1.

Hassani and Hinton31elaborated on the analytic solution and numerical solution of AEH method,and established the relationship between macro appearance and mesostructure.The governing equations were as follows:

Fig.1 Basic representation of composite asymptotic homogenization.

where Y represents the domain of the unit cell,Vyis an arbitrary virtual displacement field in Y,and Vi（y）is its component.χ is the characteristic displacement field of the unit cell,which can be obtained by modeling and solving the RUC.E represents the properties of different materials in the unit cell,andthe homogenized property of the unit cell.Based on Eq.(3),the relationship between macro appearance and meso structure is established.

2.2.Periodic boundary conditions

When calculating the heterogeneous material in meso-scale,proper boundary conditions are the key to solve the problem accurately.Assuming that the yarns distributed in the matrix are ideally uniform,the structure is periodical in meso-scale.Thus,the periodic boundary conditions can be imposed on the outer surface boundaries of the RUC.For a RUC of 3D C/C orthogonal composites,the boundary conditions can be defined as:31

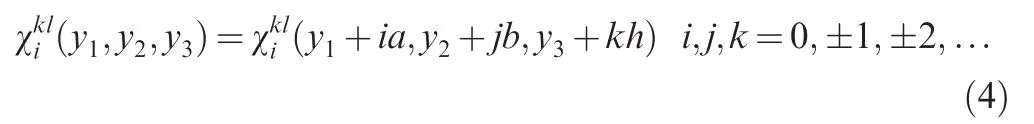
where a,b,h are the dimensions of the RUC in each axis.As the opposite faces of the RUC behave identically restrained by Eq.(4),the rotations and displacements of one arbitrary point of the RUC are fixed in order to prevent rigid body motion.

2.3.Failure criteria

The composite failure criteria can be divided into two categories,namely macroscopic failure criteria and mesoscopic failure criteria.In this work,the macroscopic failure criteria are used to determine whether the material is in the damaged state by establishing a macroscopic envelop of the material damage initiation.The mesoscopic failure criteria are used for progressive damage analysis of the mesostructure.

2.3.1.Macroscopic failure criteria

Three-dimension Tsai-Wu32second-order tensor polynomial was adopted to determine the damage initiation in macroscale:

where σiand τijare stress tensors,the second-order tensors Fiand Fijcan be calculated as:

where XT，YTand ZTare the tensile strengths of the composites in three directions,XC，YCand ZCare the compressive strengths of the composites in three directions,respectively.The S represents the shear strength of the composites.

2.3.2.Mesoscopic failure criteria

2.3.2.1.Matrix compressive failure.Based on Mohr–Coulomb compressive failure criterion,33,34the matrix fraction is determined by the stress on the fracture surface.The failure criterion is written as:

where σn，τTand τLare normal stress,transverse shear stress and longitudinal shear stress on the fracture surface,respectively,as shown in Fig.2.Assuming that the angle between the fracture surface and the normal direction is φ，σn，τTand τLcan be calculated as:

STand μT,which are independent of φ,represent the transverse shear strength of the fracture surface and the additional coefficient of shear strength,respectively.They are defined as:

where Ycrepresents the transverse compressive strength of the matrix,the φ0is the fracture angle which can be obtained by uniaxial compression experiments.

2.3.2.2.Matrix tensile failure.Tensile failure of the matrix is caused by the interaction of normal stress σnand shear stresses τTand τL.35The failure criterion is written as:

where Ytis the tensile strength of the matrix.σn，τTand τLare calculated by Eqs.(11)–(13).

2.3.2.3.Fiber compressive failure.Mayes and Hansen36considered that the fiber compressive failure is affected by the matrix shear stress around the fiber,denoted as:

where σ1is the compressive stress,Xcis the fiber compressive strength,Smis matrix shear strength.

2.3.2.4.Fiber tensile failure.The experiment results of World Wide Failure Exercise(WWFE)37,38show that fiber failure is mainly caused by tensile stress,and the maximum stress criterion is reasonable in fiber tensile failure,denoted as:

where σ1is the tensile stress,Xtrepresents the fiber tensile strength.

2.3.3.Material degradation

In the progressive damage analysis of mesostructure,if failure is detected in a particular element,the properties of that element must be adjusted according to a material property degradation model.A number of post-failure material property degradation models have been proposed for progressive damage analyses.39Most of these models belong to one of the three general categories:instantaneous unloading,gradual unloading,or constant stress,40as shown in Fig.3.In this work,an instantaneous unloading model is used.Once the failure is detected,the element stiffness matrix is multiplied by the degradation factors directly.The stiffness degradation factors are listed in Table 1.41

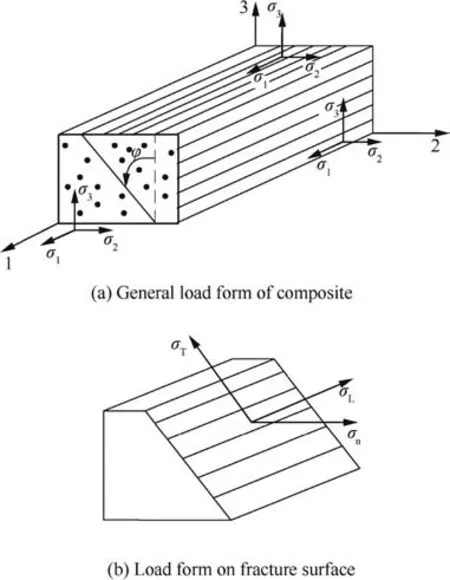
Fig.2 Stress transformation on fracture surface of composite material.

Fig.3 Post-failure degradation behavior in composites.

Table 1 Degradation factors of elastic properties.41

2.4.Analysis process

Under macro-scale loads,the yarns and matrix may be damaged in varying degrees in meso-scale.The damage will cause the reduction or failure of material constitution in meso-scale and redistribution of the macro-scale loads,which will affect the deformation and stress state of the structure directly.The multi-scale method allows for efficient and reasonably accurate predictions of the mechanical performance of the composites and the process is outlined in Fig.4.

(1)A RUC model for 3D C/C orthogonal composites is established to perform homogenization and localization analyses for obtaining homogenized mechanical properties.

(2)A composite structure model,which is a macroscopic model used to calculate global displacement and stress state,is established.The homogenized mechanical properties obtained from homogenization analysis of the RUC model and a phenomenological failure criterion is used in the model to determine the damage initiation in macro-scale.

(3)When a point stress state from the macro model causes damage,the macro-strain is applied directly to the RUC model.The meso-scale stress field and the damage of the RUC model are then calculated using the mesoscopic failure criteria mentioned in Section 2.3.2.The effective material properties are recalculated with damaged elements.

Fig.4 Analysis process.

(4)The macro-scale stress field of the structure is recalculated using the reduced effective material properties.And the macro-scale load can be incremented to the next load step.

The final failure of micro-scale element is determined by the reduction of the stiffness during the convergence iteration.In the unit cell case,a large reduction indicates that the material properties have degraded such that there is no continuous load path across the unit cell.In the numerical investigation,there was little difference found between the macroscopic predictions of the composite calculated by the value of 0.1(10%)and by the value of 0.01(1%).Value of 0.1(10%)leads satisfied precision and remarkable computing efficiency,so it is adopted in this study.

According to the strategy above,a computer code based on ABAQUS subroutine UMAT(User Defined Materials)and PDE(Python Development Environment)was developed for computing the homogenized stiffness,local stress in the RUC and the damage of 3D C/C orthogonal composites.

3.Simulations of mechanical properties

3.1.Meso-scale modeling

The different involved length scales of 3D C/C orthogonal composites are illustrated in Fig.5.In this work,crosssection of the warp,weft and Z- fibers are all fitted as rectangle approximately.Geometric parameters of the fiber yarns were recorded.For the warp and weft fiber yarns,side lengths of the cross-section rectangles are 0.62 and 0.235 mm,respectively.For the Z- fibers,both side lengths of the cross-section circulars are 0.5 mm.The smallest idealized RUC model of the 3D C/C orthogonal composite architecture was constructed,as shown in Fig.6.The length of the RUC model in x and y directions is 1.125 mm,and 0.48 mm in z direction.The total number of the elements in the RUC is 90506.

Material properties are applied in accordance with the parameters in Table 2.The yarn material is identical for warp,weft tows and Z- fibers.Symbol*refers to materials in absence of manufacturer data and the values are estimated by Eqs.(19)–(21)42and scaling data from other materials.The remainders are supplied by the manufacturer.

Fig.5 3D C/C orthogonal composites.

Fig.6 FE mesh of RUC and tows.

Table 2 Properties of yarn and matrix.

where Ft,Fc,and Fsrepresent transverse tensile strength,transverse compressive strength and shear strength of the yarns,respectively.Xmand Smare tensile and shear strengths of the matrix.and ηsare proposed as 0.5 by Cai empirical coefficient. andare stress concentration factors of the matrix and the values are in between zero and one.

3.2.Tests and simulations

3.2.1.Tests

In order to verify the RUC model and the failure criteria,a number of specimens were tested under one of the three monotonic loading conditions:tensile,compressive,and shear.The tests were designed and performed in strict accordance with ASTM C1275-10,43ASTM C1358-1344and ASTM D5379/D5379M-1245standards,respectively. The pictures of specimens and corresponding test facilities are shown in Figs.7 and 8.

Fig.7 Specimens photographs.

Fig.8 Test facilities photographs.

3.2.2.Simulation verification

The effective material properties of 3D C/C orthogonal composite were calculated utilizing the meso-scale model under unit loads in each of the six directions.The strength of the composites was also estimated by using the RUC model with failure criteria.The elastic and strength properties calculated in comparison with test results are presented in Table 3.It is verified that these values can be predicted with an acceptable level of accuracy.

Table 3 Comparison between predicted and measured values.

The diagrams of predicted stress–strain on the composite compared with test results are shown in Fig.9.The stress–strain diagrams(Fig.9(a)and Fig.9(b))on tensile and compressive loadings reveals that the predictions agrees well with the test.The response is characterized by a mostly elastic behavior,followed by a sudden brittle failure.The predicted failure stress under the tensile and compressive loadings falls within the range of values from the test specimen.But more non-linearity exhibits in the shear loading on the composite.After 60%of the ultimate failure load,the damages in RUC begins and this load level corresponds to the nonlinear start point measure in the test,as shown in Fig.9(c).The shear stiffness predicted is much lower than that obtained from the test.It is suggested that the shear modulus estimated in Table 3 may be lower than that used in the test.

A progressive failure distribution contour plot is shown in Fig.10 to illustrate how the damage affects the unit cells.The cells in red color represent the failed elements,while the blue ones represent non-failed ones.All the initial failure is generated on the interface between matrix and yarns in the three modes.The failed elements in RUC expand to the matrix first and then to the yarns in the tensile and shear loadings.However,they expend to the yarns directly in the compressive loading.It is suggested that the compressive strength listed in Table 2 is so much higher that the stress in matrix may not reach its limit.

Fig.9 Stress–strain plots under different loading conditions.

4.Multi-scale analysis of bolted connections

4.1.Global–local model

The ITPS used in hypersonic vehicle is divided into three layers,namely an upper panel,an insulation layer and a lower panel,as shown in Fig.11.The upper panel is the outer surface of the vehicle,which is made of C/C or C/SiC composites.The upper panel must be capable of bearing the critical thermal and aerodynamic loads.The insulation layer in the middle is made up of webs and lightweight insulation materials.The lower panel is made of metal alloy.The upper panel and the webs are connected using plenty of bolts.To improve calculation efficiency,a global–local finite element analysis of these bolted connections was carried out.

Fig.10 Progressive failure distribution of RUC.

The global–local analysis was performed in two steps.In the first step,the global FE model was constructed with coarse mesh.All the connections were modeled as fasteners based on mesh-independent technology in ABAQUS,46as shown in Fig.12.Two aerodynamic load cases were calculated using commercial CFD software FASTRAN,and applied sequentially to the surface of the vehicle to approximate expected flight scenarios.The flight conditions are list in Table 4.

In the second step,according to the stress results of the global model,a local FE model for the critical bolt with refined mesh was created,as shown in Fig.13.Two different bolt sizes,8 mm(M 8)and 10 mm(M 10)in diameter were considered.The element size is approximately 1.1 mm×1.1 mm×0.5 mm,which is similar to the volume of RUC.

Fig.12 Sketch of global–local model.

Table 4 Flight conditions of hypersonic vehicle.

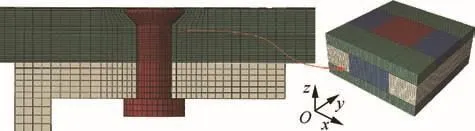
Fig.13 Section view of local model.

4.2.Boundary conditions and multi-scale simulation

The sub-model function was applied to the local model as boundary conditions to isolate the local structure to be analyzed.It uses automatic splicing to interpolate displacements and stresses at the global–local boundary.The aerodynamic loads calculated by FASTRAN were then loaded on the upper panel of ITPS.

In this work,the material used in the upper panel and bolts is 3D C/C orthogonal composite,the stiffness and strength of which were calculated as stated in Table 3.The multi-scale method was used in the region around the hole to calculate the failure process and stiffness reduction.The rest regions use the homogenization method to improve the calculation efficiency.The properties of webs and bolts are listed in Table 5.The multi-scale method was established to analyze the progressive damage of ITPS.The RUC model established in Section 3 was used to calculate the failure elements and homogenized properties,when the initial damage initiation was detected by three-dimension Tsai-Wu criteria.32

The load at which the damage begins to accumulate was not found in literature.The estimated values for prediction of damage initiation under tensile and compressive loads were 90%of the values of strengths listed in Table 3,and that for prediction of damage initiation under shear load was 60%of the values of shear strength.The estimation was based on the stress–strain plots shown in Fig.9.In tensile and compres-sive loadings,the composite exhibited brittle behavior and the RUC simulation found the damages of component phases usually initiate after 90%of ultimate failure load applied.Before the level of 90%of failure load,the damage in RUC believed trivial and ignorable.For computing efficiency,the damage analysis of RUC was launched after load level of 90%failure load.In shear loading,the composite exhibited significant nonlinear behavior.The calculation revealed that the damages in RUC began after 60%of the ultimate failure load was reached.So in this case,60%of failure load was set as the damage check point.These assumptions also corresponded to Ref.24.

Table 5 Properties of webs and bolts.

4.3.Results and discussion

Although the Mach number in load case 1 is higher than that in load case 2,the aerodynamic loads on the vehicle in load case 1 are smaller because the atmosphere is much thinner due to the higher altitude and the overload coefficient is lower.Results of both M 8 and M 10 holes of ITPS in load case 1 show no damage.On the contrary,the damages of ITPS in load case 2 are much more serious.

The circumferential stress distribution of the M 10 hole in load case 2 under a load of 40%of ultimate before the damage occurs is shown in Fig.14.The zero angle is parallel to the azimuth and pointing to the nose of the vehicle,which reveals that the connection is mainly subjected to the tensile load parallel to spanwise caused by the deformation of ITPS in windward.

Fig.14 Circumferential stress distribution of M 10 hole.

Fig.15 Section view of progressive damage of holes.

The progressive damage distribution contour plots are shown in Fig.15.Under a load of 65%of the ultimate load,the damage begins to accumulate for both M 10 and M 8 holes as illustrated in Fig.15(a)and Fig.15(b).The damage is caused by the compression between the bolt shank and the hole.The tensile damage occurs at the edge of the M 10 hole when the load reaches 81%of the ultimate,while the value of that in M 8 hole is 73%,as shown in Fig.15(c)and Fig.15(d).The comparison between the final damages is givenin Table 6.The holes of both sizes were completely damaged in the tensile direction.The damaged areas and the failed area of M 10 hole are both smaller than those in M 8 hole.It is suggested the connection with larger diameter may have a better resistance to damage.

Table 6 Damage comparison of holes of both sizes.

Fig.16 Damage distribution of M 10 with modification.

The compressive damage of the hole is caused by stress concentration at the corner,which can be reduced or eliminated by modifying the corner.As illustrated in Fig.16(a),a five-degree slope was shaped.The final damage distribution contour plot is shown in Fig.16(b).The compressive damaged area has been reduced a lot.However,the tensile damaged area increases as the whole stiffness of the connection is decreased.The damaged and failed areas increase to 4.03%and 2.10%,respectively.

5.Conclusions

In this work,an efficient multi-scale method based on the AEH method incorporating the global–local method was developed to analyze the strength of bolted connections in ITPS.A computer code was developed for computation of the homogenized stiffness,local stress in the RUC and the damage of 3D C/C orthogonal composites.The elastic behavior and failure strength of three-dimensional C/C orthogonal composites used in ITPS were also investigated and compared with the tests.The following conclusions can be drawn from this study:

(1)The longitudinal and transverse moduli along with the longitudinal Poisson’s ratio predicted by the RUC model are in close agreement with test results.The shear modulus is lower than the test result because of the underestimated yarn shear modulus.The structural strength of the 3D C/C orthogonal composites is estimated.The simulation results show an acceptable level of accuracy compared with the test results.The stress–strain plots and progressive failure distributions show that the matrix failure does not play a major role in the tensile and compressive failures.When the yarns fail,the stress–strain curve fails immediately.

(2)Based on the material properties investigated above,the strength of bolted connections used in ITPS was analyzed based on multi-scale method.Two load cases and two different bolt sizes are considered.The results show that the AEH method can be used in the strength analysis of connections to ensure high efficiency at macro-scale and precision at meso-scale.

(3)Results show the connection is mainly subjected to the tensile load parallel to spanwise.The hole failed completely in load case 2.The connection with larger diameter has a better resistance to damage in some extent.A large area of compressive damage at the corner of the hole is caused by stress concentration.An improved design is established to reduce the stress concentration.However,the tensile failures increase due to the reduction of the structure.It is concluded that the material used in ITPS cannot bear the stress in critical region.Alternatives to improve performance must be considered,including increasing the thickness of the ITPS,increasing the tensile strength of yarns and changing the architecture of the composite.

Acknowledgements

This study was co-supported by the Priority Academic Program Development of Jiangsu Higher Education Institutions and the National Natural Science Foundation of China(No.11302105).