电动汽车充电站选址规划研究

包 蕴，左忠义，殷 巍，牛 帅,邹德龙

(大连交通大学交通运输工程学院，辽宁大连 116028)

电动汽车是一种集绿色、环保、便捷于一身的交通工具，它的优势在于其本身具有节能、环保等优点。在我国大范围的推广和运用电动汽车有利于解决我国能源短缺和环境污染等问题，而电动汽车充电站可以为电动汽车大规模快速发展提供保障和动能支撑。

在环境和资源的双重约束下，电动汽车具有节能和利于环保的两大优势，这使其快速发展成为传统耗能汽车的替代产品[1]。作为支持电动汽车发展与运营所必须的配套基础设施，电动汽车充电站为电动汽车的运行提供了能源补给及维修等服务[2]。与专用停车场的规划建设不同，电动汽车充电站在布局规划过程中，不仅要考虑其建站规模和服务范围的大小，还要考虑用户充电的便捷性[3]。针对电动汽车市场发展的重要性，Hatton C E[4]提出了综合收费基础设施网络的建设，阐述了多种充电基础设施的建设规模和及其所针对的服务对象，给出充电基础设施满足的要求和条件。Sreten Davidov[5]提出了一种基于充电可靠性和服务质量要求的随机优化模型，可用于电动汽车充电基础设施的长期发展规划。刘峰等[6]针对极小极大选址的问题，提出了一种协同粒子群优化算法的选址问题求解方案，解决了基本粒子群算法易早熟、不易收敛以及缺乏多样性的问题，并用实验证明了方法的实用性。

从现有研究来看，不论国内还是国外，均侧重电动汽车及充电站的发展及作用、电动汽车充电站的设置原则以及充电设施网络构建等方面的研究，缺少针对区域经济发展以及用户充电的便捷性来进行选址的研究。鉴于上述情况，本文提出了一种考虑充电站建设成本及用户充电成本的目标优化模型，并将其代入到具有全局寻优能力的粒子群优化算法中。研究成果对城市电动汽车充电站的布局和选址具有一定的实用价值。

1 电动汽车充电站选址模型的建立

1.1 计算流程

本文在考虑电动汽车充电站选址影响因素的基础上建立数学模型，并将其代入到粒子群算法中进行最优站址的选取，具体计算流程如图1所示。

1.2 模型建立

1.2.1 电动汽车分布预测

城市内的车辆分布较为集中，大都分布在住宅区、办公区和商业区等地，城市区域内车辆(包括电动汽车)的保有量与该城市的经济发展、土地利用情况以及人口数量等因素息息相关。现假设规划区域内共有电动汽车NQ辆，小区C的电动汽车NC辆，NC计算公式如式(1)所示。

(1)

其中，fceil(·)为取整函数；RQ表示规划区域内的人口总负荷；Rc表示小区C的人口负荷。

规定划分出的每个小区的几何中心为电动汽车充电的需求点，一个充电站内的需求点到该充电站的距离为电动汽车充电的行驶距离。

1.2.2 电动汽车充电站选址模型

本文主要考虑用户充电途中和等候充电的耗时成本以及充电站建设和运营成本两方面来建立选址模型：

minZcost=FC1+FC2+FC3.

(2)

其中，Zcost表示电动汽车充电站的总成本；FC1、FC2、FC3分别表示电动汽车充电站建设成本和年运营成本、用户充电途中年耗时成本、排队等候年时间成本。

1.2.2.1 充电站年建设成本和运营成本

年建设成本常指充电站在初始建设时期的基础设施建设费用和设备购置费用，包括配电系统、充电系统、监控系统等[7]。建设成本主要与充电站数量有关，数量越多，成本越高[8]。运行成本主要包括设备折旧费用、充电站工作人员费用、日常运营维护与管理费用等[9],可按建设成本的一定比例取值。

(3)

TjsMj=αTjc(Mj).

(4)

其中，J表示充电站集合，Mj表示充电站j内设有的充电站数量，j∈J；Tjc(Mj)表示充电站j的年建设成本函数，通常取决于充电站内充电站的数量；Tjs(Mj)表示充电站j的年运行成本函数，一般按照建设成本一定比例核算；r0表示贴现率，指将未来资产折算成现值的利率；n为充电站的折旧年限；α表示运营成本与建设成本之间的折算系数。

1.2.2.2 用户充电途中年耗时成本

决定耗时成本的主要因素为用户从需求点到充电站所行使的距离，用户充电途中年耗时成本(一年以365天计)表示为：

(5)

其中，I表示需求点集合；δ表示城市内出行时间成本系数，它能将时间成本转换为价值成本；Ni表示需求点i内的电动汽车数量；tij表示充电车辆从需求点到达充电站的时间。

1.2.2.3 排队等候年时间成本

每个电动汽车充电站都可被描述成一个排队系统，文献[10-11]将电动汽车充电系统归结成是M/M/S模型，其进入充电站的过程符合泊松分布，而其充电过程服从负指数分布。但电动汽车在排队等待充电过程中对排队等候时间期望特别敏感，即待充车辆进入充电站后更关心排队等候时间，通常排队等候时间期望不应超过10min。

电动汽车用户排队等候时间期望：

(6)

电动汽车用户到站排队等候年时间成本计算公式为：

(7)

1.3 约束条件

1.3.1 充电站间距不等式约束

λijDpq≥Dmin,p,q∈J，p≠q.

(8)

其中，λij表示从需求点i到充电站j的非直线系数；Dpq为充电站p到q的直线距离；Dmin为充电站间最小距离。

1.3.2 需求点到充电站距离的不等式约束

(9)

其中，dij表示从需求点i到充电站j的空间直线距离；dmax为快充需求点到充电站的最大距离；ri为充电站的服务半径。

1.3.3 系统稳定性不等式约束

δj<μMj.

(10)

其中，μ表示充电机的平均服务速率。

2 案例分析

本文以大连市沙河口区为例进行充电站的选址规划。沙河口区是辽宁省大连市的一个市辖区，位于大连市区西部，总面积48.32平方千米，管辖9个街道办事处、89个社区居民委员会。根据沙河口区街道的划分，本文将其划分成9个交通小区，并在每个区域内选出一个合适的充电站站址。大连市沙河口区街道划分如图2所示。

2.1 相关参数的设定

在模型计算时，相关参数如下：区域总人口RQ=659015，区域电动汽车总数NQ=519，贴现率r0=0.08，折旧年限n=20年，折算系数α=0.1，出行时间成本系数β=30元/h，单车日快充概率q=0.05，非直线系数λij=1.2，充电站服务半径ri=3km。

权重改进的粒子群算法中参数如下：粒子种群数为24，学习因子c1=c2=2，惯性权重的范围为0.4～0.9，最大迭代次数为2000次。

2.2 优化结果

在以街道划分的每个区域内随机选取6个需求点，根据式(1)(2)的模型运用粒子群优化算法计算出沙河口区布局和选址结果,如表1所示。

表1 各区域电动汽车及充电机配置数量

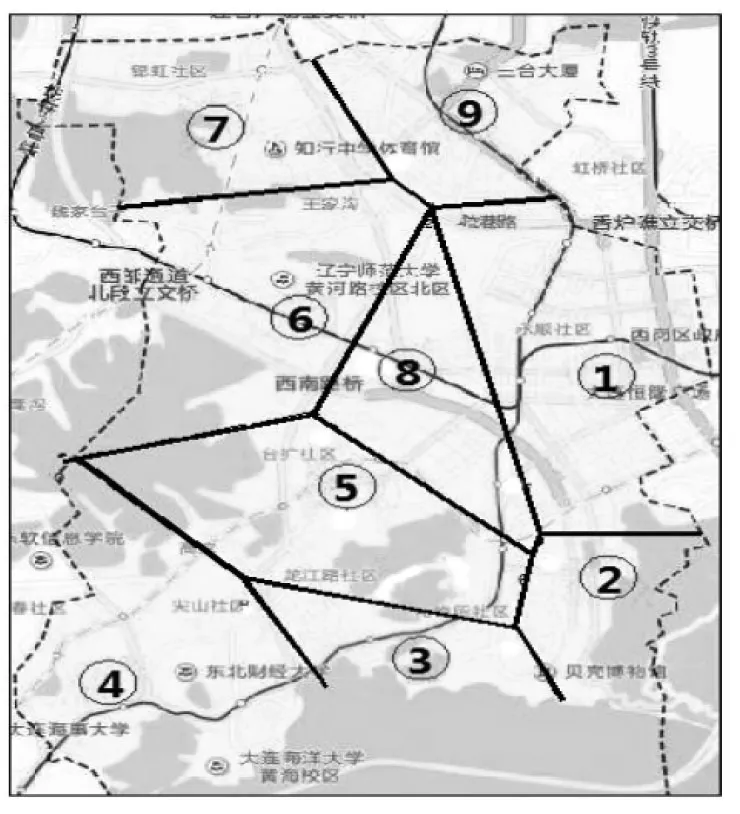
充电站服务范围如图3所示。图3中虚线内部为此次研究区域—沙河口区，①～⑨代表9个充电站的站址，内部黑色实线代表Voronoi图凸边形的边界，凸边形表示充电站的服务区域。可见充电站站址分布均匀，临近服务区域重心，且服务区域划分明确，能够有效地解决充电站选址规划问题。这里需要说明的是，已选取的充电站站址仅为计算所得到的结果，在实际建站时还应考虑土地实际使用性质，即是否适宜建立电动汽车充电站，若所选站址内不允许建立充电站，则应对充电站站址进行微调，考虑相关影响因素进行二次选址，这也是今后研究的一个思路方向。

充电站相关成本的计算如表2所示。由表2可知，由于不同区域内需求点位置、人口与经济情况等不同，从而建站费用、运营成本、途中年耗时成本和年排队等候时间成本也不同。其中建设成本是总成本的主要影响因素，充电机设置越多，其建设成本和运营成本越高，对应总成本就越高。而充电机的设置台数主要由该区域内人口及电动汽车数量来决定，因此在经济较发达地区其建设成本和运营成本都较高。

表2 充电站优化结果

3 结语

本文以大连市沙河口区作为选址对象，分别对其9个街道进行了电动汽车充电站的布局和选址，沙河口区属于大连市的核心区，经济较发达，因而本文在选址时主要考虑了其经济发展情况、人口数量以及用户充电过程的便捷性，使充电站的建设和运营成本以及电动汽车用户的充电成本最小。将得出的站址作为Voronoi图的基础点，划分出了9个充电站的服务范围。本文的选址模型符合沙河口区实际情况，验证了改进权重的粒子群算法在选址这一课题中的有效性，且证明了Voronoi图具有划分充电站服务范围的能力。寻求充电站内充电机的科学配置方法，在满足用户充电需求的情况下尽量减少充电站的成本支出是今后研究的重点。