简易帆板摆角控制系统建模与MATLAB仿真

李海霞

(忻州师范学院电子系，山西忻州 034000)

目前国内外有关帆板摆角控制系统的研究，大多侧重硬件电路的直接设计。这些设计由于存在被控对象模型的不确定性，也未提前对系统建立精确的数学模型，所以在PID参数调节和整定上带有一定盲目性[1]。

控制系统设计步骤是先对系统建立精确的数学模型，然后通过MATLAB仿真调整PID参数，从而为实际设计制作中PID参数具体数值提供参考，可大大缩短PID参数整定时间，给软件编程调试带来方便。当然如果遇到的控制系统比较复杂，数学模型就无法精确建立，可以通过模糊PID控制或者内模控制器来实现对系统较为理想的控制。考虑到帆板摆角控制系统的组成构件较为常见，可以借鉴相关的角度控制系统建模方法进行精确建模，故本文将尝试首先对被控对象(帆板摆角和执行器)建模，再通过MATLAB软件仿真，寻找最优PID控制参数。

帆板摆角控制系统属于多变量、线性控制系统。系统的输出受到多个变量的影响[2]。控制系统的建模是系统分析和设计的基础，只有对系统建立精确的数学模型，才能通过MATLAB软件的Simulink工具仿真得出最优的PID控制参数下的输出波形，从而为软件编程提供可靠的PID参数，缩短软件编程和调试时间[3]。

1 系统组成及工作原理

系统由主控模块、角度检测模块、风扇电机驱动模块、显示模块、按键输入模块、电源模块、声光报警模块等构成[4]，如图1所示。主控模块的核心是PID控制器，PID控制器的原理图如图2所示。角度检测模块通过角度传感器实时采集帆板摆角输出信号y(t)，通过对比测量角度与预先设置的角度r(t)，算出摆角偏差e(t)。风扇电机驱动模块采用L298N驱动芯片，L298N芯片是较常用的直流电机驱动芯片，能够对电机转速的快慢进行平滑调节，减小调节过程中电机本身对风扇的影响。

由图2可知，PID控制器是根据系统的被控量输出值y(t)与给定值r(t)进行比较，得到误差信号e(t)，控制器通过对其进行比例、积分和微分加权运算处理，获得控制器的输出信号u(t)，并将其作为被控对象的输入信号。PID控制器输出u(t)的表达形式为：

(1)

连续PID控制器的传递函数模型为：

(2)

其中,KP、Ki、Kd均为常数。

2 系统建模

直流电机电压U与电机转速n之间的关系：

(3)

风扇风速v1与直流电机的转速n的关系，可近似表示为：

(4)

为了简化推导过程，本文假设风是以一个柱状的形态行进，而且风是吹进一个管底关闭的管子中，当风到达管子的底端时，速度迅速降为0，且散到管底周围的力可以忽略不计。在管中取一段长为h的风柱，密度设为ρ，风速为v1，管底面积为s，则在时间t内会有质量为m的空气通过，且表达式为：

m=ρsh=ρsv1t.

质量为m的空气在管子的底部，假如F为管子底部受到的风力大小，那么应用动量定理可得：

Ft=mv1=ρsv1tv1=ρsv12t.

因此风力F与风速模型为：

F=ρsv12.

(5)

将式(3)代入式(4)得到电机转速n与风力之间的关系：

F=ρsKn.

(6)

在日常生活中，影响风力大小的因素不仅是电机转速，还有很多其它量,例如风扇叶片面积的大小、叶片的长短、叶片的厚度、叶片的数量、叶片的形状等因素都会影响风速。改变风扇扇叶的长度，可以改变风力大小；改变风扇的叶片数，也可以改变风力的大小；改变风扇扇叶的叶片形状，使其有更好的流线型和适当的弯曲度，以及其它的各种方法都能改变风扇的风力大小[5]。为了简化模型以利于仿真起见，本文只研究通过改变直流电机的转速来调节风速，从而改变风力的大小。

帆板摆角受力分析如图3所示。

设物体质量为m，其重力用G表示。当风扇打开时，便可产生一个风力，用F表示。重力与风力同时作用在帆板上，使帆板产生与竖直方向成θ的夹角。帆板的运动是在一定的摆角范围内的向心运动，船对帆板的拉力和重力与风力沿帆板方向的合力提供向心力。设帆板的速度为v，垂直于帆板斜向上，角速度为ω，加速度为a，帆板面积为S，长为r。设垂直于帆板方向为x轴，沿帆板的方向为y轴。

帆板沿x轴的受力分析：

Fx-Gx=Fcosθ-Gsinθ=max.

(7)

(8)

将式(3)代入式(8)可得：

空气密度ρ的确定：通常情况下空气密度的取值为1.225kg/m3。

帆板参数在本文预设值，其中质量m为3kg，长度r为1m，宽l为0.5m，面积S为0.5m2。

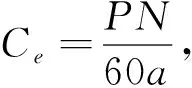
(9)

3 MATLAB仿真结果

仿真利用MATLAB的Simulink工具，运行框图如图4所示。

经过多次反复整定PID参数得出，在比例系数为Kp=90、积分系数为Ki=1、微分系数Kd=7.1的情况下可以获得最佳输出响应曲线图,如图5所示。

此时，调节时间为0.4s，超调量为2%。兼顾了响应的快速性和平稳性指标，稳态误差为0。

4 结语

本文从影响输出值-帆板摆角的最终因素出发，不断反推，最终找出电动机输入电压与帆板摆角之间确立的时域模型，经拉氏变换到频域，最终得到控制系统被控对象的传递函数模型。在确定被控对象数学模型的基础上，可通过MATLAB仿真寻找到PID控制器中最优的比例、微分、积分系数，从而指导实际控制器参数的设置，可以大力地缩减实际操作中PID控制器的整定时间，节省人力、物力。