基于反演设计的变质心飞行器滑模变结构控制器设计

陈升泽，张 旋，解春雷，郑小鹏

（中国运载火箭技术研究院研究发展中心，北京，100076）

0 引 言

变质心飞行器采用安装在内部的可移动质量块作为控制系统的执行机构，通过改变飞行器的质心位置达到气动配平和姿态控制的目的。变质心控制方式与传统的空气舵、推力矢量和姿控喷管等控制方式相比具有一定的优势：a）其控制装置安装在飞行器的内部，不会影响飞行器良好的气动外形；b）不需要考虑控制装置的烧蚀，避免了飞行过程中空气舵烧蚀引发的控制参数时变问题；c）避免了姿控喷管带来的侧喷绕流问题和燃料消耗导致的质心变化问题；d）采用一体化设计思想，利用飞行器的已有设备作为可移动质量块，如伺服系统的电池、战斗部等，有利于实现飞行器的轻小型化设计。在再入飞行器变质心控制技术方面，国外开展了大量的理论研究和工程实践。目前，中国对变质心飞行器的研究仍处于理论研究阶段。国内外学者针对单质量块滚动控制[1]、双质量块自适应控制[2]、三质量块动态拟控制[3]、变质心/RCS复合控制[4]等进行了相关研究。

变质心飞行器姿态控制系统存在强非线性、通道耦合和控制耦合等特性[5]；飞行器再入过程中气动烧蚀带来的气动外形变化难以用数学模型准确描述，这也给控制模型带来了不确定性因素；再入过程力学环境复杂，现有的风洞试验很难模拟高马赫数下的飞行环境，气动干扰难以估计。因此，控制系统要实现飞行器稳定、高精度控制，有一定困难，需对此进行深入研究。本文将一种基于滑模变结构[6]的强鲁棒控制技术用于变质心飞行器的姿态控制，旨在提高控制精度和飞行器抗干扰能力。

1 变质心飞行器动力学模型

1.1 问题描述

变质心飞行器建模与传统的再入飞行器系统建模存在区别，在伺服机构的作用下可移动质量块相对弹体发生相对运动，变质心飞行器在空间中的运动可以看作为弹体与质量块的组合运动，属于多刚体运动学范畴，利用Newton-Euler矢量力学的方法可以建立其运动学模型。

本文研究的变质心飞行器两侧安装一对水平差动副翼。俯仰、偏航通道用可移动质量块进行控制；水平差动副翼用于克服非对称烧蚀和质量块移动对滚动通道的耦合影响，实现滚动通道的稳定控制。在飞行过程中，飞行器没有推力的作用，利用空气动力完成机动飞行，因此，飞行器仅受地球引力和空气动力影响，飞行器结构外型与质量块安装位置[2]如图1所示。

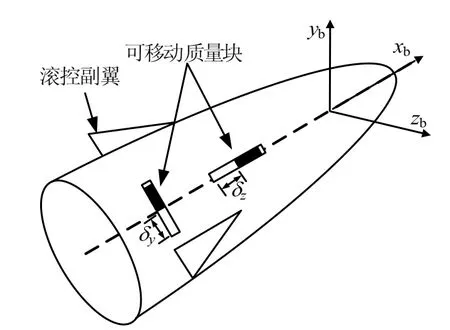
图1 变质心飞行器示意Fig.1 Moving Mass Control Vehicle Schematic

1.2 坐标系及变量符号定义

飞行器建模时所用的坐标系及符号定义如下[8,9]：

变量符号定义如下：

a）飞行器的质量为 m0，可移动质量块质量分别为m1， m2，系统的总质量为可移动质量块的质量比分别为：

b）设l1， l2表示可移动质量块在飞行器体坐标系下的轴向坐标，该参数可以设计但确定后不随时间变化；为控制参数。因此，滑块在飞行器体坐标系下的位置分别表示为和

1.3 动力学模型

为获得变质心飞行器俯仰、偏航通道的简化姿态控制模型，做出如下假设：a）飞行器安装有差动副翼，认为滚动通道稳定；b）由于飞行器内部结构布局的限制，可移动质量块位移和移动速度均为小量，它运动过程中的附加惯性力矩的影响与气动力相比可以忽略；c）由于飞行器在飞行过程中不进行大姿态机动，因此攻角α、侧滑角β、角速度yω和zω均为小量；d）飞行器为结构对称体，惯性积为零。

变质心飞行器俯仰、偏航通道的姿控动力学模型如式（1）至式（4）所示。

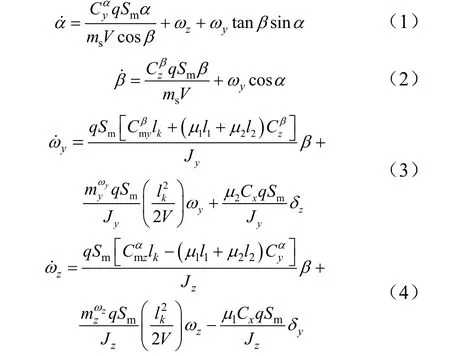
式中 Cx为阻力系数；为升力系数对攻角的导数；为侧向力系数对侧滑角的导数；为阻尼力矩系数；为力矩系数对侧滑角的导数；为力矩系数对攻角的导数；分别为飞行器的参考面积和参考长度；q为动压；V为飞行器速度。

为简化模型的形式，做出以下定义：

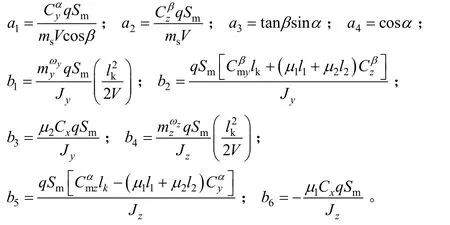
因此，式（1）至式（4）可以写为下式：

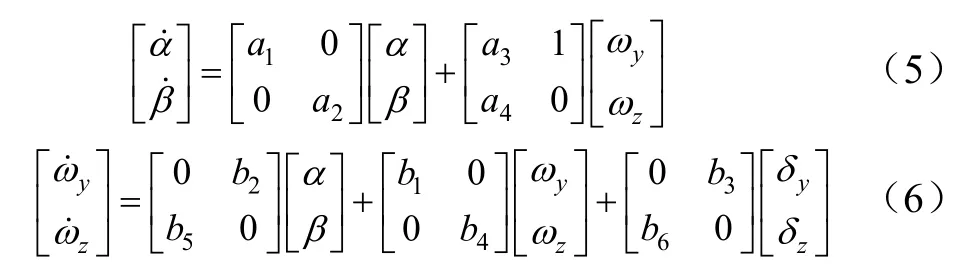
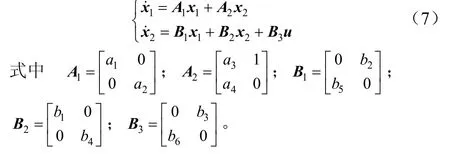
1.4 控制律设计

反演设计[7]通过从系统的最低阶次微分方程开始，在每一步设计中，通过引入虚拟控制使相应的子系统满足滑动条件，并最终设计出真正的控制律。

a）设计虚拟控制量。

对1z，2z求导得：

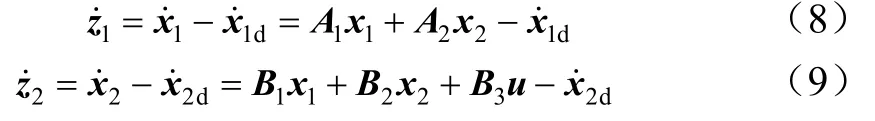
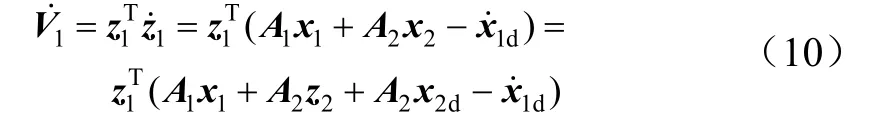
将设计的虚拟控制量2dx 代入式（10），可得：

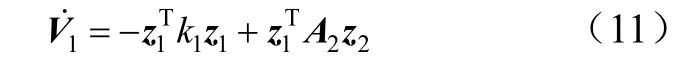
b）设计切换函数。

将第1步设计的李雅普诺夫函数 V˙1代入式（12），可以得到：

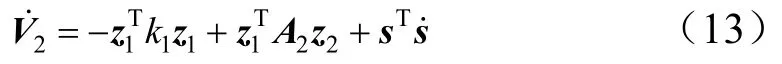
对切换函数求导后，代入式（13），可得：

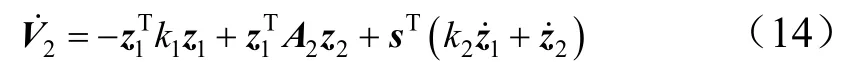
将式（8）和式（9）代入式（14）：

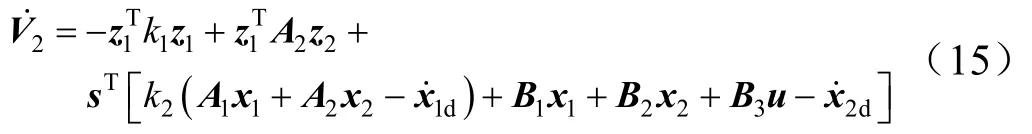
采用一种变指数趋近律[1]设计滑模控制器，其表达式为：变指数趋近律避免了指数趋近律的缺点，指数趋近律运动点逼近切换面是一个渐进过程，不能保证有限时间内到达。增加一个变速趋近项使运动到达切换面时速度很小，并缩短了趋近时间，可以保证有限时间内到达切换面。结合变指数趋近律设计如下：

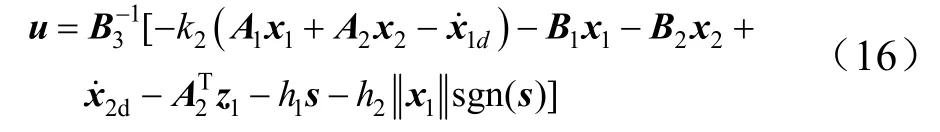
式中1h，2h为大于零的常数。

将所设计的控制律代入式（15），可以得到：

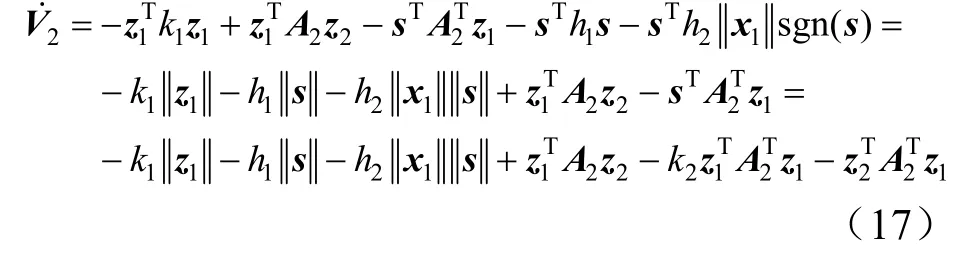
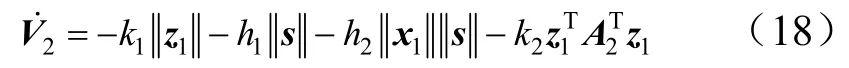
综上所述，20≤˙V，设计的控制器能够满足李雅普诺夫稳定性判据。

非连续滑模控制器在穿越滑模面时会出现抖振，为消除仿真中的抖振现象，缓解结构切换的不连续性，采用式（19）所示的连续函数将原有继电特性连续化：

式中 δ为边界层厚度，是很小的正常数且可调节参数。

将式（19）代入式（16）中，滑模变结构控制律如式（20）所示。

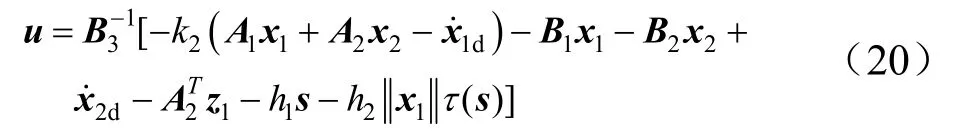
2 仿真分析

为验证本文提出的控制律合理有效，利用飞行过程中的特征点参数开展俯仰、偏航通道的仿真分析。飞行器的控制系统结构如图2所示。飞行器结构参数[2]如表1所示。

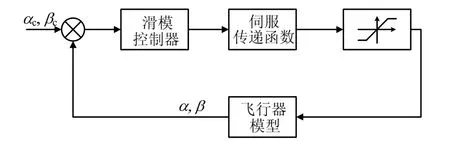
图2 飞行器控制系统结构Fig.2 Moving Mass Control Vehicle Control System Structure α—攻角；cα—飞行器攻角指令；β—侧滑角；cβ—飞行器侧滑角指令

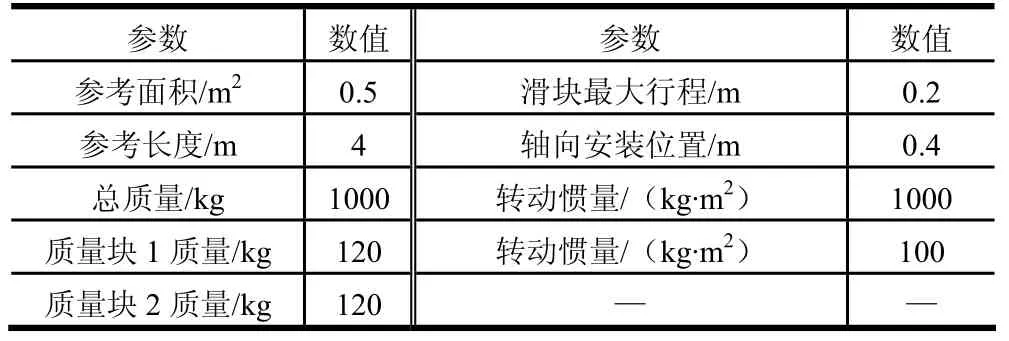
表1 飞行器参数Tab.1 Moving Mass Control Vehicle Parameter

飞行器初始攻角、侧滑角为0°，初始角速度yω，zω为0（°）/s。设攻角指令为10°、侧滑角指令为5°，仿真时长为5 s。为验证控制律的抗干扰能力，在2 s时给攻角一个随机扰动。根据式（16）未采用连续函数的控制律进行仿真，结果如图3～6所示。

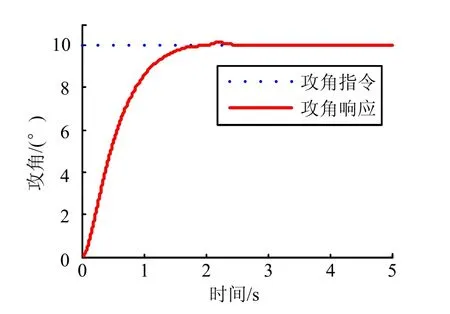
图3 攻角响应仿真曲线（未采用连续函数）Fig.3 Impact Angle Response Simulation Curve（No Continuous Function）

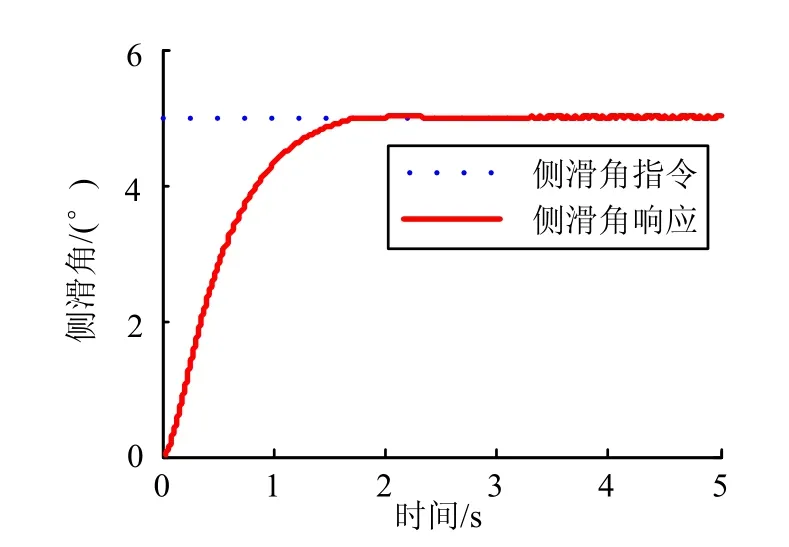
图4 侧滑角响应仿真曲线（未采用连续函数）Fig.4 Sideslip Angle Response Simulation Curve（No Continuous Function）

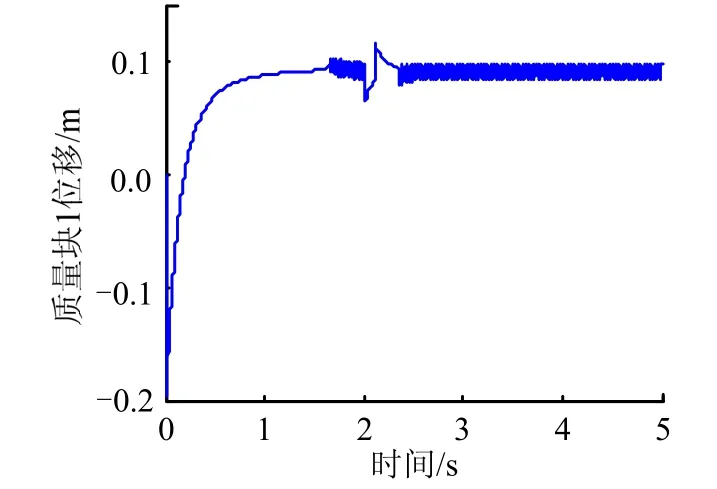
图5 质量块1位移仿真曲线（未采用连续函数）Fig.5 Mass 1 Displacement Simulation Curve（No Continuous Function）

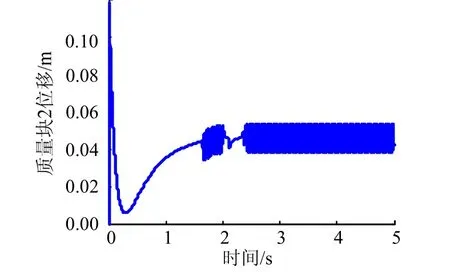
图6 质量块2位移仿真曲线（未采用连续函数）Fig.6 Mass 2 Displacement Simulation Curve（No Continuous Function）

从仿真结果可以看出，虽然式（16）给出的控制律能够使系统较快跟踪指令信号，但是质量块的位移出现了抖振的现象，导致攻角和侧滑角的响应也出现抖振。根据式（20）采用了改进的滑模变结构控制律进行仿真，结果如图7至图10所示。

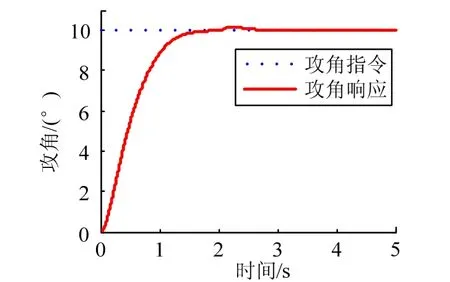
图7 攻角响应仿真曲线（采用连续函数）Fig.7 Impact Angle Response Simulation Curve（Using Continuous Function）

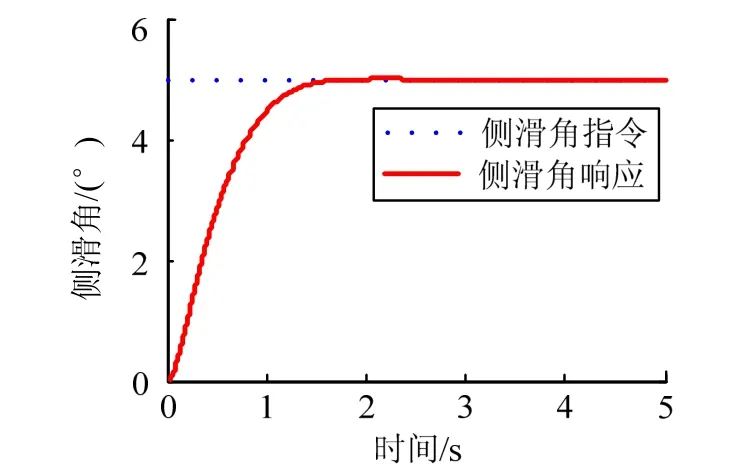
图8 侧滑角响应仿真曲线（采用连续函数）Fig.8 Sideslip Angle Response Simulation Curve（Using Continuous Function）

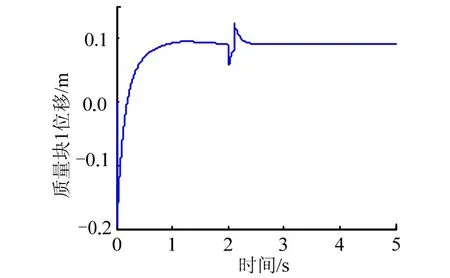
图9 质量块1位移仿真曲线（采用连续函数）Fig.9 Mass 1 Displacement Simulation Curve（Using Continuous Function）

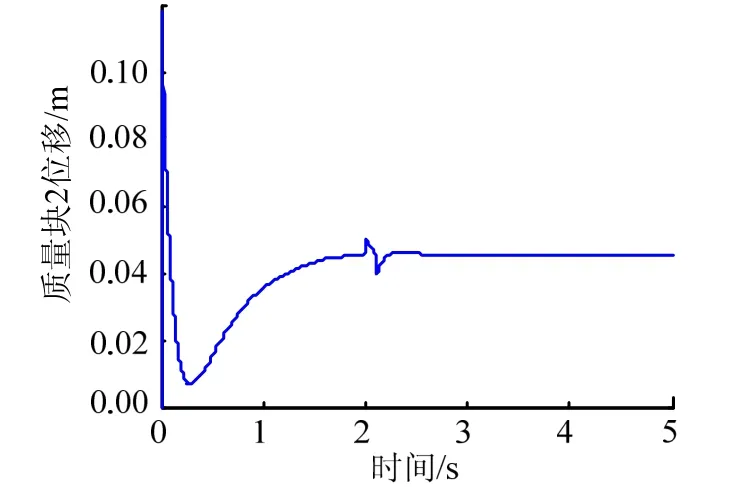
图10 质量块2位移仿真曲线（采用连续函数）Fig.10 Mass 2 Displacement Simulation Curve（Using Continuous Function）

从图7至图10可见，在1.5 s左右飞行器的攻角和侧滑角收敛至配平值，所设计控制律能够迅速跟踪指令信号，从质量块的位移可以知道，仍具有一定的控制余量。在2 s时由于加入了干扰信号，攻角和侧滑角响应曲线出现一定的波动，但波动的幅度不大，并能很快收敛至稳定值，证明控制律具有一定的鲁棒性，对外界的瞬时干扰能够及时响应并克服。仿真结果中并未出现抖振现象，表明采用改进的滑模变结构控制律，克服了原有继电特性的抖振，获得了良好的控制效果。

3 结 论

本文针对双滑块变质心再入飞行器的姿态控制问题，基于Newton-Euler矢量力学的方法，建立了飞行器俯仰、偏航双通道动力学模型；采用反演设计的思想，设计了一种基于滑模变结构的控制律，并采用连续函数取代原有控制律中的非线性函数，消除了仿真中出现的抖振现象；通过仿真分析表明，该控制律实现了飞行器的姿态稳定控制，其攻角和侧滑角能够快速跟踪指令信号，并具有一定的鲁棒性，能够克服外界的未知干扰。

本文的变质心飞行器的控制律设计方法仍需要进一步的研究：a）完善被控对象的模型，建立三通道动力学模型，考虑滚动通道对俯仰、偏航通道的影响；b）基于自适应的方法完善控制律的设计，进一步提高控制律的鲁棒性；c）考虑飞行器的六自由度运动，开展飞行器再入全程的制导与控制研究。