一类直线与圆问题及其解法的探析
2018-08-15李雅萍
李雅萍
(江苏省木渎高级中学 215156)
直线与圆的方程是解析几何的基础知识,它不仅涉及几何知识,也涉及代数知识,综合性较强.下面先从苏教版必修二课本的一道习题说起.
一、问题呈现
例1 已知圆C:x2+y2-2x+4y-4=0,是否存在斜率为1的直线l,使以l被圆C截得的弦AB为直径的圆过原点?若存在,求出直线l的方程;若不存在,说明理由.
二、解法探究
本题考查了直线和圆的位置关系,分析题目会发现,“以AB为直径的圆过原点”这句话,从不同的角度和切入点,可以有不一样的解法.设以AB为直径的圆为圆D,则AB有着三个身份:AB在直线l上,AB是圆C的弦,AB是圆D的直径.
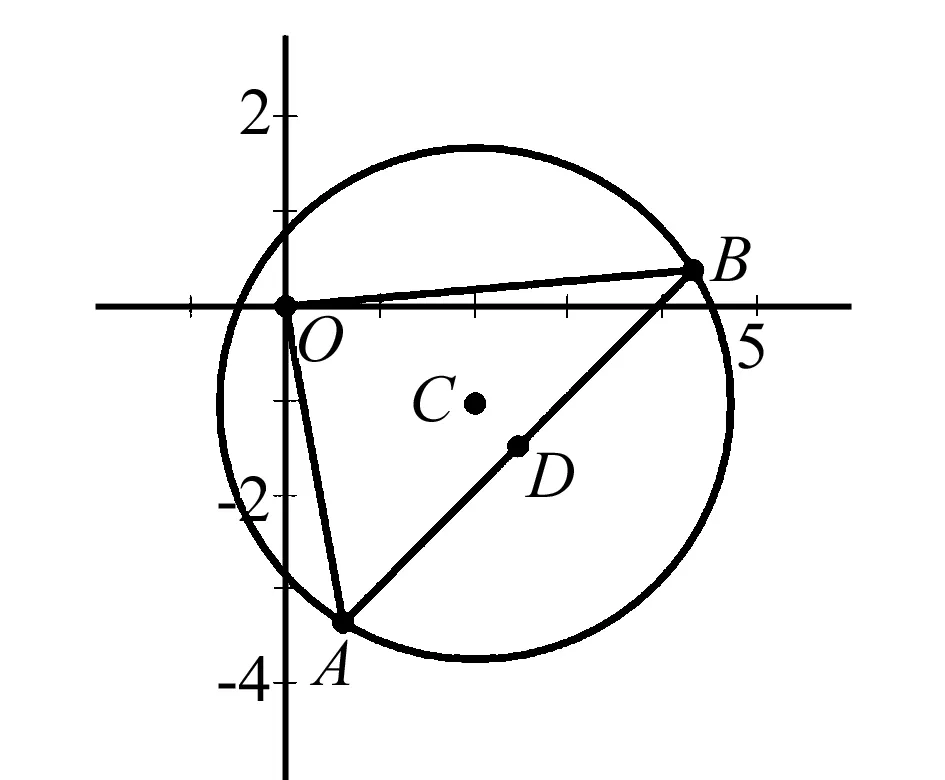
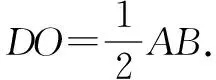
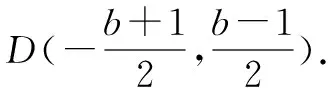
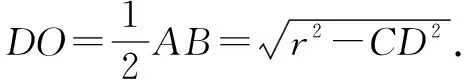
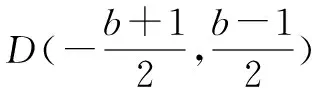
综上所述,存在满足条件的直线l,其方程为y=x+1或y=x-4.
解出b=1或b=-4后,还要记得检验直线l与圆C相交,这是很多同学解题时都容易忽略的.
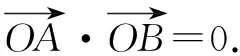

联立直线与圆的方程,消去y,得2x2+2(b+1)x+b2+4b-4=0②.
角度三从圆系方程出发,用点在曲线上、曲线与方程的关系来解题.由AB的身份一和身份二,除了联立方程组,还可以用圆系方程来解答.若直线Ax+By+C=0与圆x2+y2+Dx+Ey+F=0相交,则过两公共点的圆系方程为x2+y2+Dx+Ey+F+λ(Ax+By+C)=0(λ∈R).具体解题过程如下.
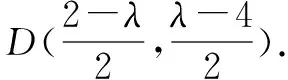
综上所述,存在满足条件的直线l,其方程为y=x+1或y=x-4.
不过,不少同学用解法三求解这道题时,大多中途受阻,一个重要的原因就是“AB为直径”未能转化成“圆心D在直线l上”这一隐含条件.
以上可见,遵循所归纳的思路原理,沿着任何一种思维路径都可解决问题.
三、反思感悟
三个角度的解法中,“以AB为直径的圆过原点”分别与垂径定理、勾股定理、数量积、韦达定理、点在直线上这些知识点联系起来,用了等量代换、设而不求、联立方程组、待定系数法等方法.
罗增儒教授将学会解题分为四个步骤:记忆模仿、变式练习、自发领悟、自觉分析.模仿是对基本模式加以认识并积累的过程;变式是在简单模仿的基础上主动实践;自发领悟是内化解题知识;自觉分析是对解题过程进行自觉反思,使理解进入到深层结构.对于一类问题的探析,首先是基于记忆模仿与变式训练的“模式识别”,然后是基于自发领悟与自觉分析的“算法设计”.数学题多似海,变化万千,但许多问题及其解法在本质上是一样的.如果我们能有效地抓住问题、方法的本质,就能实现举一反三.
