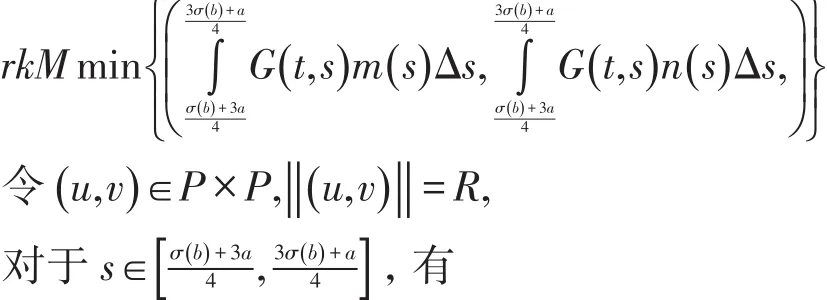时间模上二阶方程组边值问题多个非负解的存在性

张 英

(山西大同大学数学与计算机科学学院，山西大同037009)

时间模上的二阶非线性动力学方程组的边值问题研究的不多，给出方程组

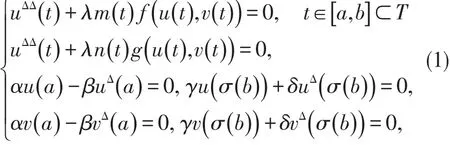
至少有两个正解的存在性，在2000年马如云讨论下面方程组解的存在性。[1]

引理1设E是一个巴拿赫空间，定义一个锥P⊂E,0＜r＜H＜R 是实数，D={ }x∈P|r≤‖x‖≤R,φ，D→P是一个紧的全连续算子，满足

则 φ有两个不动点 x1,x2满足

引理2令是方程组（1）的解，当且仅当

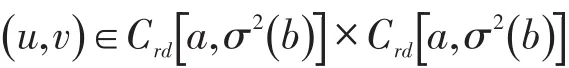
是下面积分方程组的解

引理3格林函数G(t,s)满足

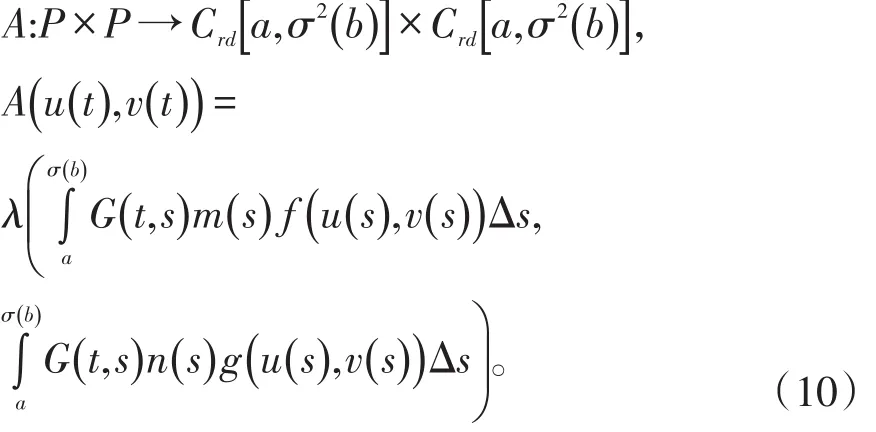
定理1让λ＞0,则方程组（1）至少有两个非负解u,v满足下面条件

(A3)存在一个H＞0 满 足其中，

证明分四步来证明：

第一步：设(A1)（1）成立，存在 r＞0,要么

这里M满足

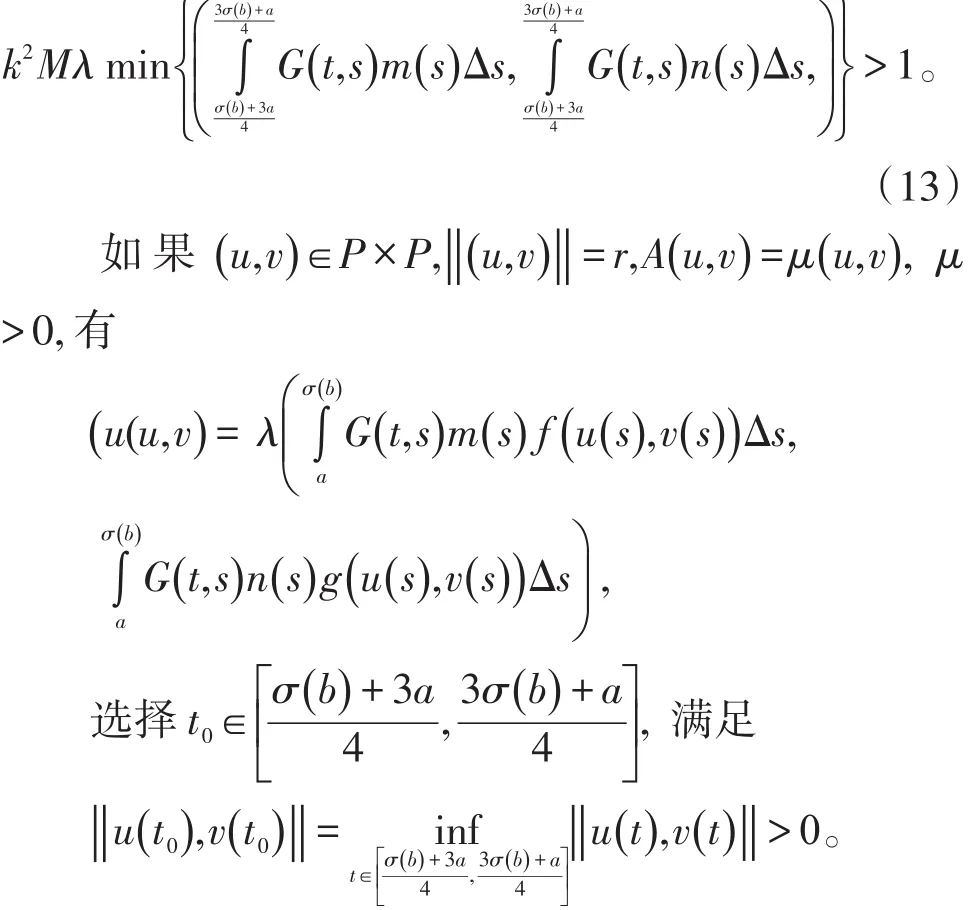
那么由（7），（11)和 (13)得到

第二步：设(A2)（1）成立，存在 R′＞0,要么

那么由（7），（16)和 (17)得到

所以 μ＜1。

第四步：设(u ,v) ∈P×P,‖( u ,v) ‖=r,如果 (A1)（1）成立，对于，有

无论哪种情况得到