指向学生高层次思维能力培养的行动研究*

◎ 陈 赣 黄自敏 丁 玉

高层次思维能力，是上海市绿色指标中的一个维度，主要测量学生在学科上的高级认知水平。高层次思维能力是学生适应未来社会所必备的能力，然而目前的教学中，重复机械的低层次思维学习活动占据了学生的大量时间。改变这样的现状需要从课堂教学入手，在学科的课堂教学中培养学生的高层次思维能力。为此，松江区课题组在厘清高层次思维内涵，形成高层次思维操作框架的基础上，设计课堂中培养学生高层次思维能力的干预路径，通过各学科教师的课堂教学实践，形成课堂中培养学生高层次思维能力的初步策略。

一、高层次思维的内涵及其操作框架

阅读已有文献，可将研究者对高层次思维的阐述分为以下几个方面：一是阐述高层次思维的特征；二是阐述高层次思维的类别，即哪些思维属于高层次思维（如批判性思维、创造性思维等）；三是阐述高层次思维的思维过程，即其思维过程应该是怎样的，具备怎样的特点；四是认为思维是具有一定层次的，并阐述高层次思维的层次和特点；五是认为思维是具有一定品质的，并阐述高层次思维的品质特点。

在归纳文献、各方访谈，以及学科专家和教育专家的研讨结论基础上，课题组提出了高层次思维的初步操作框架（见表1），该操作框架包括一级指标、二级指标，以及对二级指标的描述。各学科再在该通用框架的基础上，形成各学科的指标描述。

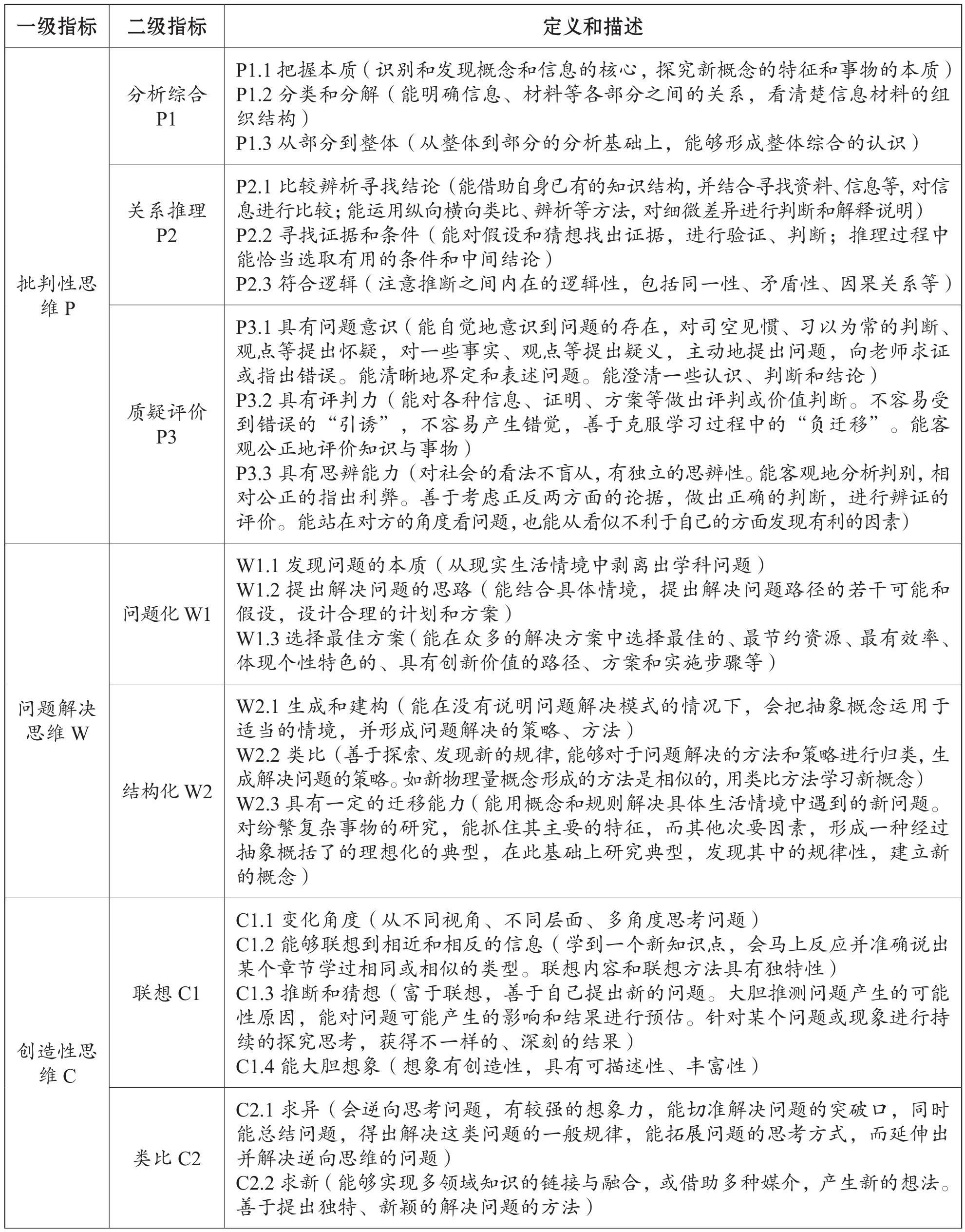
表1 高层次思维操作框架

（续表）

二、课堂中培养学生高层次思维能力的干预路径

形成高层次思维总体操作框架后，松江区各学科教研员根据学科特点形成各自学科高层次思维的框架，并根据操作框架进行课堂观察。在此基础上，课题组教师尝试在课堂教学中开展干预式的教学研究。干预研究的总体原则是在不影响教师正常教学安排的前提下，对某些内容的教学进行干预。根据高层次思维的框架，批判性思维的培养从分析综合、关系推理、质疑评价三个维度展开，创造性思维的培养从联想和类比两个维度展开，问题解决能力的培养从提出问题、将问题结构化、寻找策略三个维度展开，元认知能力的培养从纠错、优化两个维度展开。这些维度都是层层递进、彼此相连的。

以数学学科为例，开展教学实践研究的教师提前两周确定课堂教学干预点，并积累课堂中培养学生高层次思维能力的案例。干预点的设置示意图如图1所示。

案例的分析示意图见图2。

图1 课堂教学环节干预点示意图

三、课堂中培养学生高层次思维能力的策略

（一）通过质疑、比较和评价等，培养学生的批判性思维

思维批判性的高层次表现为思维的论证性。教师可以从以下几个方面着手促进学生批判性思维的发展：一是在教学目标的设定上体现批判性的要求。在设计教学目标时，使用涉及和体现“批判性思维”的目标动词，发挥教学目标的导向性，借助学科知识的载体，使批判性思维技能训练得到落实。另外，教师也可教授给学生一些运用批判性思维的具体方法，例如根据学科特点，通过思维导图、表格等方式提高学生的信息组织概括能力和问题解决能力。三是在作业中设计开放性问题，调动学生进行多角度思考。

图2 案例分析示意图

以七年级的一节数学课为例，教师在要求学生给出尽可能多的解法后，要求学生对方法的优缺点进行质疑、比较和分析，在质疑、比较分析中培养学生的批判性思维。

【课堂片段1】

例题 如图3所示，在△ABC和△A′B′C′中，当∠C=∠C′=90º，AB=A′B′，BC=B′C′时，证明：△ABC≌△A′B′C′。

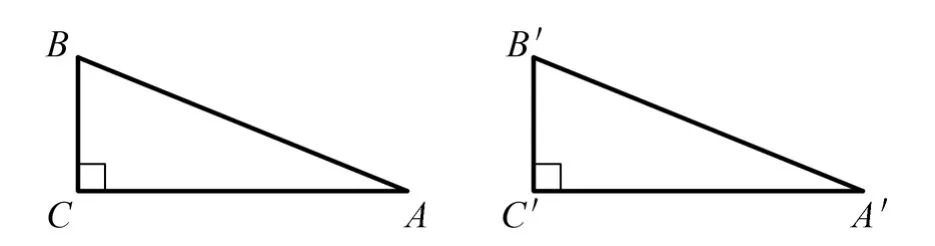
图3

生：估计会有4种组合图形。（动手操作，展示如图4所示的4种不同拼法。）

师：这4种能拼合吗？能拼合关键是什么？

师（追问）：在能拼合的4种图形里，你能证明哪几种？

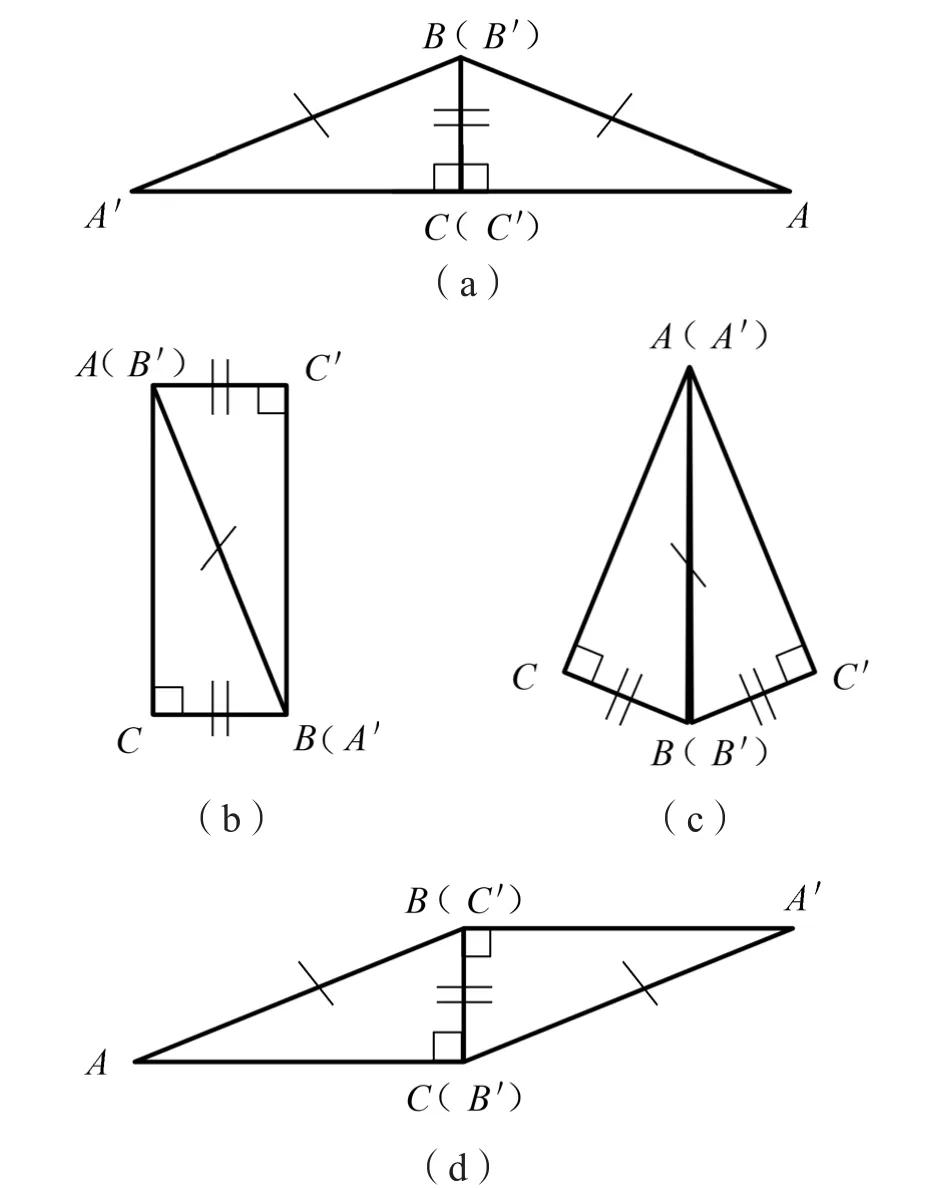
图4

证明步骤：

a.让学生说说图3的证明。

教师引导学生质疑：这位同学的证明过程，大家是否完全同意？ （留一些时间）

“等边对等角”这个定理前提是什么呢？那△A′BA是三角形吗？证明A A′是一条边也就是证明什么呢？那怎样证明点A、C、A′在一条直线上呢？

b.让学生说说图4的证明。

c.图4（b）（d）这两种拼法目前我们证不出，主要的困难在哪里呢？

师：由已知条件要想证明全等，只要再证明一个锐角或者一条直角边相等就可以了，而这两种拼法没有创设出边相等或者角相等的条件，所以目前不能证明，留待以后来解决。

让学生探究在给定了一条直角边和斜边以后，怎样把一个三角形画出来，强化了他们的动手能力，同时也增强了他们的团结合作能力，另外可以让他们经历知识从感性认识到理性认识这个过程。

本次课是设计了干预点的批判性思维培养的一次数学课，课堂中教师让学生经历操作—猜想—验证—归纳的知识形成过程，体会解决问题的常用方法。让学生懂得，有些证明方法是可以借鉴的，并渗透化归、演绎的数学思想。在对图4（a）进行证明时，学生很容易默认为三角形时，而忽视三点共线的证明。教师充分利用此处，通过几何推理的严密性，培养学生的批判性思维。

（二）鼓励学生敢于创新，培养学生的创造性思维

在课堂教学中，首先，作为教学的组织者，教师要具有创新意识和创造性教育的能力，能够触类旁通，举一反三；教学中能够从不同角度考虑问题，用多种方法和手段组织教学；要善于进行灵活多样、富有弹性的教学设计。其次，要让学生最大限度地参与教学活动，努力营造一个全体学生积极思考的氛围，鼓励学生积极参与教学活动的全过程，利用课堂讨论、小组活动、探究实验等方式，刺激学生大脑思维，培养学生思维的灵活性和深刻性。第三，利用形式丰富的课外活动培养学生的创造性思维，让学生在好奇中探索知识，在活动中锻炼思维。

有机化学是高中化学学习中难点，课题组教师以有机化学最核心的知识碳碳键的连接方式为引，由学生来按照价键规则创造物质的方式来消除学生对有机物的陌生感，从而引领学生正式踏入有机化学的学习之门。而创造物质的过程，就是一个创造性思维和提升的过程。课堂片段示例如下。

【课堂片段2】

教师首先抛出问题：只有碳、氢两种元素，你能组合成多少种物质？规则：①碳元素只能形成4条共价键；②氢元素只能形成1条共价键。接着教师首先呈现出甲烷的结构式，目的在于为学生创造时提供思路。

【活动一】由学生创造碳碳间单键连接。教师评价学生创造出的碳碳间单键连接，剩余价键被氢饱和的乙烷、丙烷等，并鼓励学生继续创造下去。

（说明：教师首先对不符合价键规则的地方进行纠正，强调创造一定要符合规则，加深规则意识的体验。最主要的是总结创造点，碳碳间可以连接成键。总结的意义在于，学生可能是顿悟式无意识地创造出新物质，通过学生的反思总结，寻找出内在的原因和逻辑，让创造性更上一个层次，并用于指导接下来的创造过程。）

【活动二】评价学生创造出的环状物质和有支链的链状物质。鼓励学生继续创造过程。（说明：体验原创性思维和模仿性创造的差异。强调原创性创造固然可喜，模仿性创造也是一种重要的创造方式。从分层教学的角度来说，一个开放性的问题可能适合更多同学，能力强的可以是原创性思维，能力弱的可以是模拟性创造。）

【活动三】学生呈现出类似立方烷这样的结构，然后师生共同总结创作历程。

（说明：从一个碳原子的甲烷，到链状，到环状，到立方烷这样的结构，内在的逻辑是碳原子间连接方式沿着从“点—维—二维—三维”逐渐演变的过程，体现了创造思维的有序性。）

【活动四】跳出定势，再次创造

（说明：当学生认为创造已经走到尽头的时候，教师再次提出，还有很多种可能。此时，教师适时地点拨：创造最怕的是定势和僵化，点线面体一路走下来，表明有序性既有利于我们的创造，也可能是阻挡创造的绊脚石。一条路走不通时，一定要回到原点，思考问题的本质和核心——碳碳间的连接方式。于是，含双键的乙烯出现了，炔也出现了。至此，学生对于仅有两种元素可以构成多种元素的元素观，价键的规则意识，碳碳间连接方式的多样性是构成有机物种类繁多的原因有了亲身的感受和直接的认识。）

（三）让学生学会反思和总结，培养学生的元认知能力

元认知具体包括对自身的反省和对学习策略的思考，如明确自己哪些方面做得好，哪些地方需要改进，能及时自我调整，总结错误经验，通过反思找到适合自己的学习方法等。教师可通过训练学生反思自己的学习活动，来提高学生的元认知能力。一方面要将学习反思贯穿于日常的教学活动中，如利用每节课下课前的几分钟，引导学生回忆本课的主要内容并对自己的掌握情况进行自我评价，明确哪些内容是自己掌握的，哪些内容是没有理解的。另一方面是在作业和练习中落实学习反思，如要求学生写好当天所学知识的主要内容和重难点，同时写出学习中遇到的困难。这样做既便于教师在批改时，有效地了解学生对知识的掌握情况，从而更有针对性地帮助学生克服难题；又督促学生对自己的学习进行反思，并不断调整学习行为，以提高学习效果。

【课堂片段3】在英语阅读课中，教师常常遇到的一个难题就是生词太多，如何解决这类难题，课题组教师给学生充足的时间，自己先理解，并对自己理解错误的地方进行自我修正，培养学生思维的反思性。以初中英语7BU5为例，以下是教授生词the Luck Fairy的教学片段：

T: There were three people in the story.Who were they?

S1: They were Fred, Dor is and the Lucky F...

T: The“Lucky” or “Luck”？（等待10秒）

S1: ‘Luck’.（学生思考并修正）

T: Good.The Luck Fairy.Eyes on the screen（仙女图片）.She is the Fairy and ‘Luck’ is her name.What does the Luck Fairy usually do?Do you know? （ 等 待 10秒）She has magic powers.（继续等待5秒）

S1: She usually helps poor people.

T: Very good.The Luck Fairy usually brings people what? （继续等待10秒）

S2: Good luck.

T: And wishes.What else? She usually helps people realize...? （继续等待8秒）

Ss & T: Their dreams and wishes.

正确读出仙女的名字看似简单却实属不易，学生一开始回答便把Luck读成Lucky，说明他不清楚这两个词的词性，形容词lucky修饰Fairy表示仙女是幸运的，而the Luck Fairy中名词Luck是幸运仙女的名字。课题组教师对于学生的错误没有忽视或跳过，先停顿并发问（The “Lucky” or “Luck”?），等 待 10秒旨在留有时间给学生思考自己的答案并修正；再用英文解释帮助学生理解仙女的名字，并引导他们进一步回答问题“What does the Luck Fairy usually do?”旨在为下文要求学生回答仙女想要帮助Fred和Doris，要给他们带来好运等问题作铺垫。

课题组教师在这个问题上等待10秒换来的是学生自己思考后的优质答案，这样的课堂问答模式应该得到更多的尝试，这是训练学生在回忆和理解的基础上进行再度思考，培养学生思维的反思性，它也证明了等待时间的运用对学生和教师都是受益无穷的。

（四）培养学生的高层次思维能力需要给学生充分讨论和思考的时间

由于教学时间紧、教学任务重，许多教师养成了迅速前进的习惯，没有认识到让节奏慢下来鼓励学生思考的潜在价值，尤其是当学生回答不出或犯错时，教师一定要留足够的时间供学生思考作答，并根据教师的反应和反馈对自己的答案进行再思考和修正。

当学生想出一种方法后，教师可以再提出进一步的要求“还有其他方法吗？”若看学生一下子想不出来，可以说：“相信同学们经过仔细思考肯定还会有新的解题方法，课后你们可以把想出来的方法告诉我。”课后，总是有几个同学又想出了几种方法。可用延时评价的方法，对学生提出的或回答的问题不予即时评价，创设积极和谐的教学氛围，留给学生充裕的时间和广阔的思维空间。

【课堂片段4】关于八年级数学“二元一次方程练习”研究课

问 题1： 已 知 关 于x的 方 程（k-3）x+kx+1=0，求证：不论k取何值，方程总有实数根。生A回答：“要使方程有实数根，需要证明△=k-4（k-3）≥0。”大部分学生都同意生A的这种解法。针对他们由于思维定势而产生的错误解答，教师没有做出即时评价，只是微微一笑，然后快速地扫视全班，注意到平时沉稳细心的生B一脸疑惑，于是问：“你是否有不同的见解？”生B怯怯地而又肯定地质疑道：“老师，该不会是您出错题了吧？这道题是要在k≠3的条件下方程才有实数根。”生B话音刚落，生A也立刻反应过来：“是啊，我刚才的解法忽略了二次项系数不为零这个条件了。老师，难道您出错题了？”看着学生沉浸在“成功”的喜悦中，教师没有急于做出即时评价，而是想让他们自己找出“错误”，体验别样“成功”。“老师到底有没有出错题呢？先看看下面这道题。”

问 题 2： 已 知 关 于 x的 方 程（k–3）x+kx+1=0，当x取何值时，该方程分别为一元一次方程和一元二次方程，并判断此时该方程是否存在实数根。学生很快完成解答。因为上一题还“驻守”在黑板上，这时有的学生已经明白了老师的暗示，思维又转回上一题中，开始了热烈的讨论。“老师没有出错题，是我们错了！”教师微笑点头，请生A分析错误：“此题没有说给出的是一元二次方程，如果k=3时，方程为一元一次方程，同样有实数解x= –1/3 ,而且我们在证明△≥0时已经要求k≠3，不符合题目的求证。”教师追问：“同学们能细心观察，发现问题，勇于质疑，通过类比联想，得出解决问题的正确方法。那么，请同学们反思刚才的错误，对于日后的解题有何启示？”学生从思维定势及知识点的掌握等方面追根溯源，各抒已见，畅所欲言。

因此，我们在课题实践研究中，一方面要求教师精设提问，不追求问题的数量，提高问题的质量，提一些能引发学生深入思考，能培养学生高层次思维能力的、开放性的问题。另一方面，教师在提出需要学生思考的问题后，应该留给学生充足的时间进行思考、讨论。各学科由于教学内容多，不是所有的内容都允许学生有充足的时间进行思考和讨论，但至少要选择一部分的内容，教师引导学生思考、争辩、得出和验证结论等，让学生学会思考的方法。