大跨度RPC铁路简支箱梁有效宽度研究

吴延伟

(中铁第一勘察设计院集团有限公司 西安 710000)

近年来，随着我国高速铁路的迅速发展，活性粉末混凝土(reactive power concrete, RPC)这一具有高耐久性、高抗压强度、高抗裂性[1]等优异力学性能的高性能新型复合材料受到铁路桥梁专业越来越广泛的关注和研究。RPC超低高度T形梁也已成功应用于我国铁路工程中，如迁曹铁路和蓟港铁路[2]。而高速铁路对桥梁的刚度要求较高，箱梁相校于T形梁整体性能好、材料布置合理、动力性能好而在高速铁路中更广泛应用，但是目前铁路工程中RPC箱型梁的应用还处于空缺。RPC由于其优异的力学性能可以将传统箱梁构件尺寸做的更轻薄从而降低梁体自重，增大简支箱梁的跨越能力，从技术、经济和景观各方面较目前的普通预应力混凝土箱梁有较大的提升和改善，因此，对RPC箱梁的研究具有重要的工程意义。

RPC材料强度及性能介于钢材与常规混凝土之间，其截面构造尺寸也处于钢箱梁与常规混凝土箱梁之间，现行设计规范对有效宽度计算是否可应用于RPC箱梁，尚无相关结论。本文针对RPC双线简支梁，结合薄壁箱梁基本理论，通过有限元程序数值分析，研究了不同荷载工况、高跨比、顶板厚度、横隔板数量对跨中断面顶、底板的剪力滞效应的影响规律，并计算出对应的有效宽度系数。同时与《公路钢结构桥梁设计规范》《公路钢筋混凝土及预应力混凝土桥涵设计规范》相关有效宽度计算结果比对。从而为大跨度RPC双线简支梁设计研究工作提供参考及依据。

1 剪力滞效应及规范计算有效宽度

1.1 剪力滞效应机理及剪力滞系数

带肋梁结构在外力作用下产生的弯曲内力可通过梁肋的剪切变形传递给板。事实上，剪应变在向板内传递的过程中是不均匀的，在梁肋与翼缘板的交接处最大，随着与梁肋距离的增加而逐渐减小，这种由于翼板的剪切变形而造成的弯曲正应力沿梁宽度方向不均匀分布的现象称为剪力滞(后)效应[3-4]。

图1显示了沿翼缘板宽度方向的弯曲正应力变化规律。

图1 板单元应力与应变示意图

在板上表面取一微小单元体，初始形状为方形，加载后变成菱形。假定τxy作用在dxdydz单元的一边，在其对边则为τxy+ dτxy，其不平衡力dF可用泰勒级数展开，然后略去第二项及以后各项，得到Y轴的剪应力的变化值

(1)

利用单元体x方向力的平衡，可以得到

(2)

消去dzdxdy,得到一维平衡方程

(3)

式(3)揭示了剪应力与正应力的关系，由于翼板剪切变形的不均匀性，引起在弯曲作用下远离梁肋翼板纵向位移滞后于靠近梁肋的翼板之纵向位移，所以其弯曲正应力的横向分布呈曲线形状。

为了方便分析比对，采用式(4)和式(5)计算截面有效宽度和有效宽度系数。

(4)

(5)

式中：be为桥面板有效宽度；b为桥面板实际宽度；σ为截面应力；σmax为截面最大正应力；λ为有效宽度系数。

1.2 规范计算有效宽度

国内现行铁路桥梁设计规范有关有效宽度的计算在TB 10092-2017 《铁路桥涵混凝土结构设计规范》(以下简称《混凝土规范》)有对应计算表格，在钢结构设计规范中未有明确表述，但在JTG D64-2015 《公路钢结构桥梁设计规范》(以下简称《钢桥规范》)中有详细的计算公式，故分别采用公路钢结构与铁路混凝土结构计算有效宽度，如式(6)和表1所示。

(6)

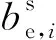
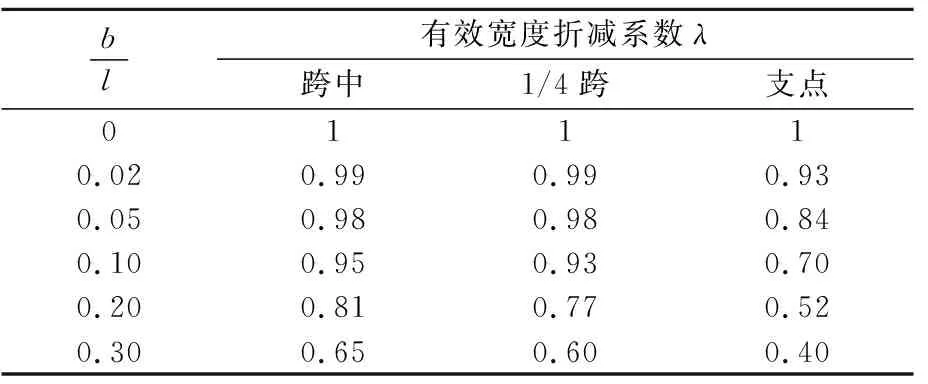
表1 简支箱梁有效宽度折减系数

2 截面形式及计算模型

受刚度、强度、经济性，以及施工便利性等因素控制，RPC箱梁截面形式各异。本次研究截面形式为单箱单室结构[5]，箱梁跨度72 m，顶宽12.6 m、底板宽6.0 m，具体截面见图2。

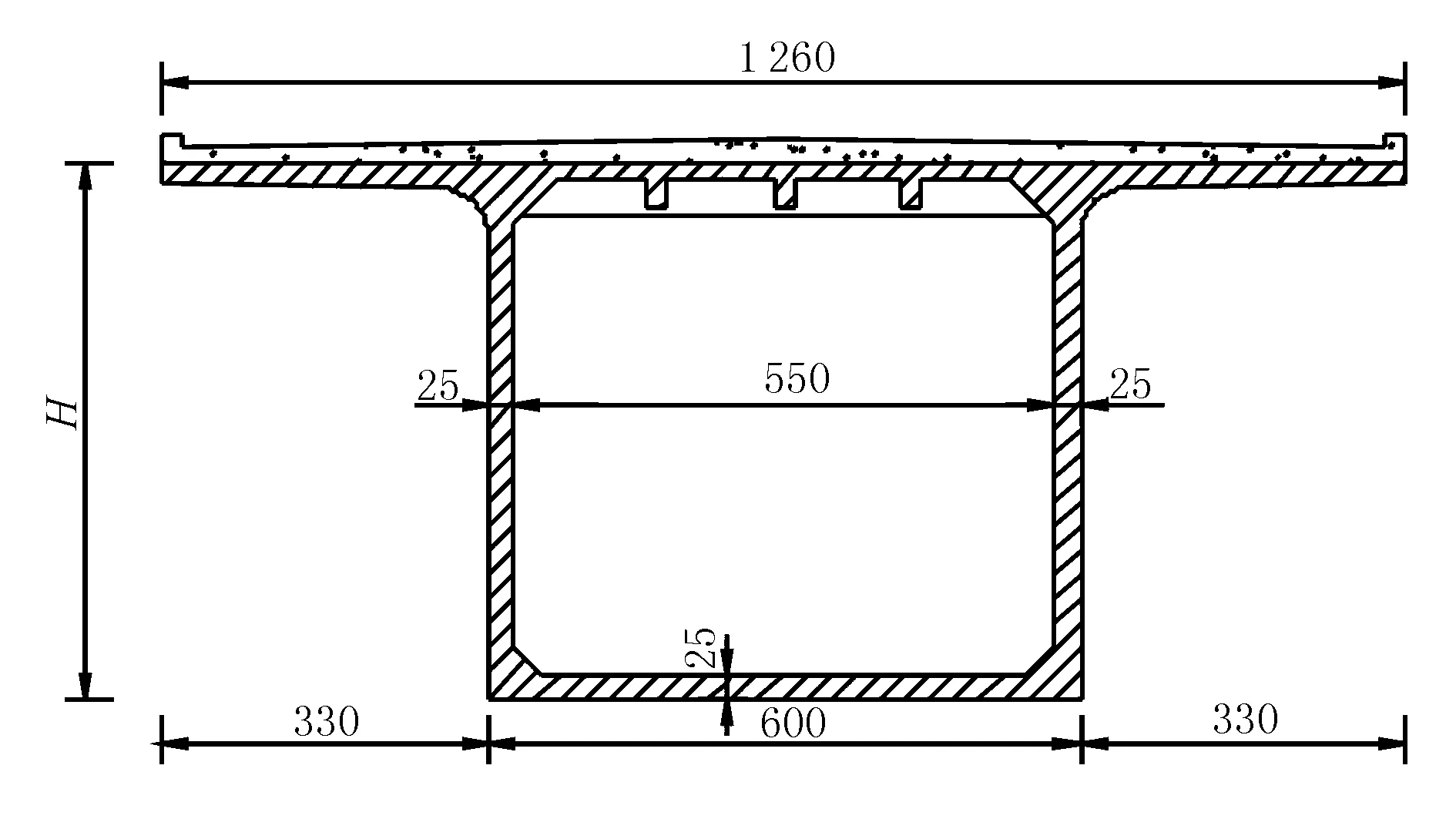
图2 截面构造图(单位：cm)

活性粉末混凝土容重取26 kN/m3；二期恒载按350 km/h高速铁路有砟轨道设置，为200 kN/m；活载采用高速铁路ZK活载。

活性粉末混凝土材料力学参数：弹性模量E=48 GPa；立方体强度fck=120 MPa；轴心抗压强度fc=80 MPa，轴心抗拉强度fct=6 MPa[6]。

分析采用大型有限元软件ANSYS 15.0，顶、底板及腹板采用薄板单元来模拟，选取SHELL63单元。

模型见图3。

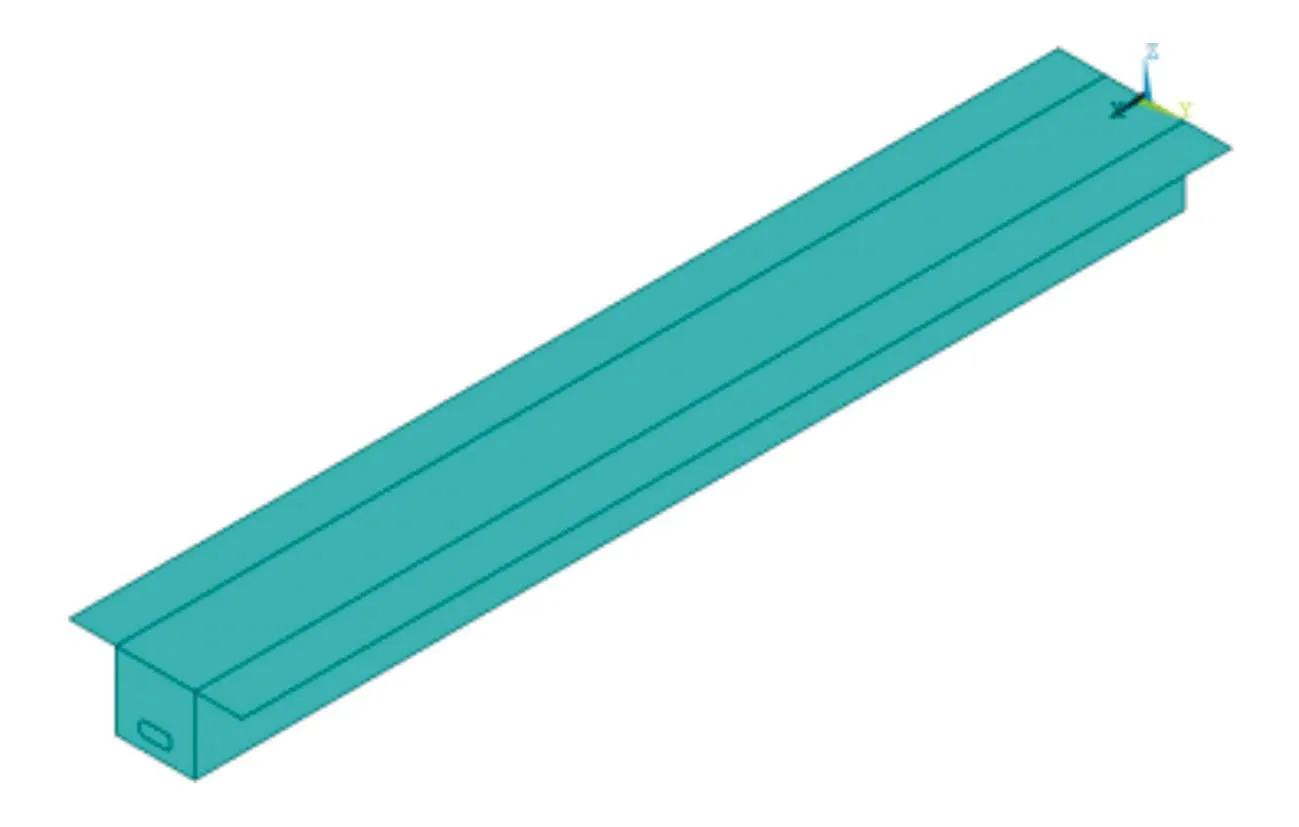
图3 有限元模型

3 剪力滞效应分析

3.1 自重、二期、活载作用下剪力滞效应

为了使自重、二期、活载作用下顶、底板剪力滞效应方便比对，将3种荷载工况下跨中顶、底板正应力标准化，即将3种荷载工况下跨中顶、底板正应力均除以其绝对值最小值，标准化后跨中顶、底板的“正应力”横桥向分布见图4，其中，以顶板中点为横坐标原点。

图4 顶板正应力标准化

由图4可见，跨中顶板在二期荷载作用下剪力滞效应最为显著，有效宽度系数达到0.70，自重和ZK活载的剪力滞系数分别为0.89，0.98。

图5显示跨中底板在自重荷载作用下剪力滞效应最为显著，有效宽度系数为0.95，二期和ZK活载的有效宽度系数均为0.99，其中以底板中点为横坐标原点。

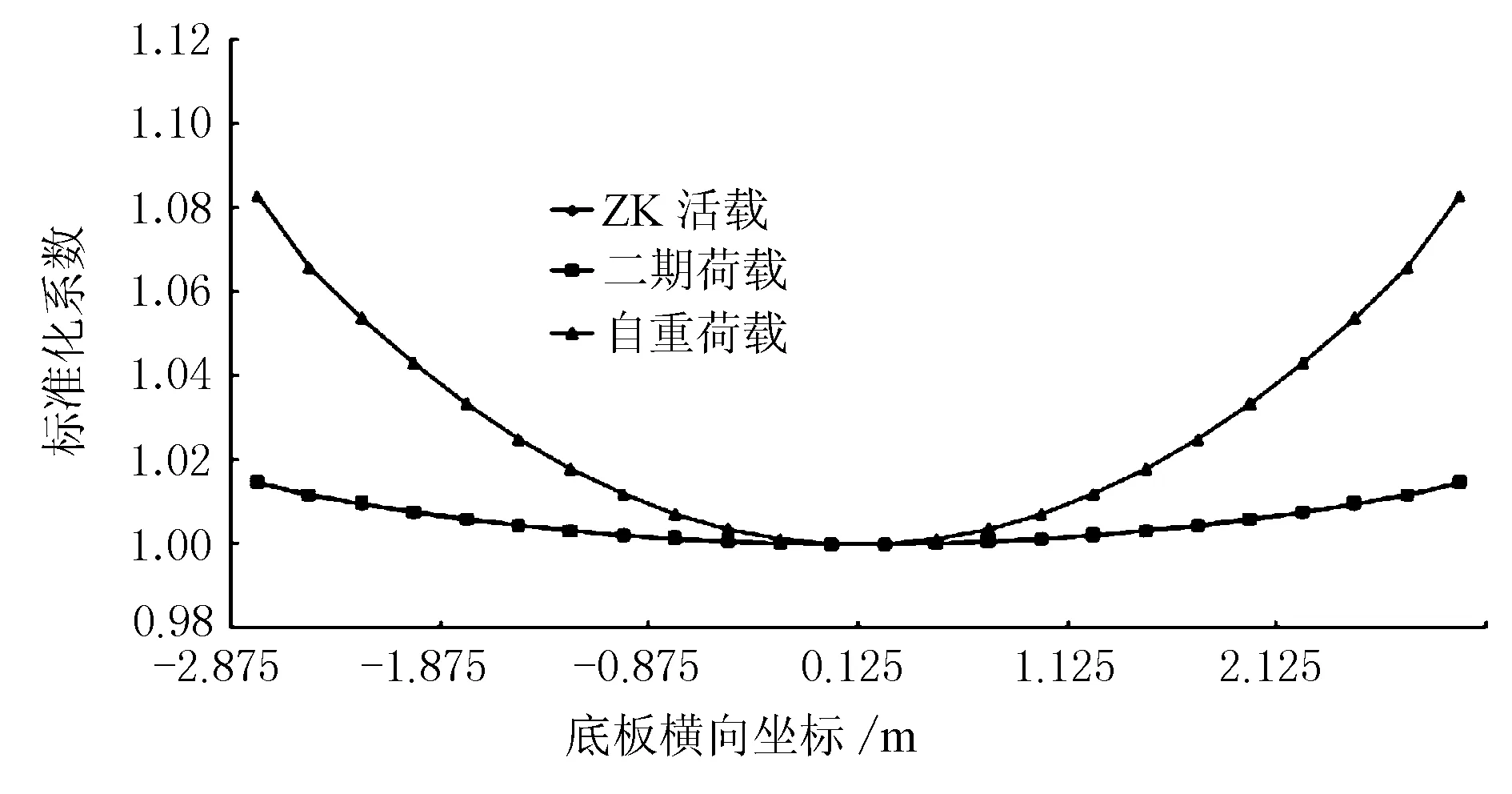
图5 底板正应力标准化

3.2 梁高对剪力滞效应影响

由3.1知跨中顶板剪力滞效应在二期荷载下最为显著，因此，本节以及后面2节的剪力滞效应分析均在二期恒载下进行。本节保持箱梁截面各尺寸不变，分析梁高在4.8，5.2，5.6，6.0 m 4种情况下跨中截面顶、底板的剪力滞效应。

跨中顶、底板的正应力横桥向分布标准化见图6、图7，横坐标原点定义方式同图4、图5。

图6 顶板正应力标准化

图7 底板正应力标准化

由图6、图7可见，随着梁高增加，顶板有效宽度系数从0.73减小到0.68；梁高增加了25%，有效宽度系数减小6.8%；底板有效宽度系数保持0.95不变。在工程实际中，对应跨径的梁高受刚度及构造等控制,变化幅度较小,因此梁高变化对跨中顶、底板剪力滞效应影响可忽略不计。

3.3 顶板厚度对剪力滞效应影响

本节保持箱梁截面其他尺寸不变，分别分析顶板在0.12，0.16，0.20，0.24 m厚度时，二期荷载下跨中顶、底板剪力滞效应。跨中顶、底板的正应力横桥向分布标准化见图8、图9，横坐标原点定义方式同图4、图5。

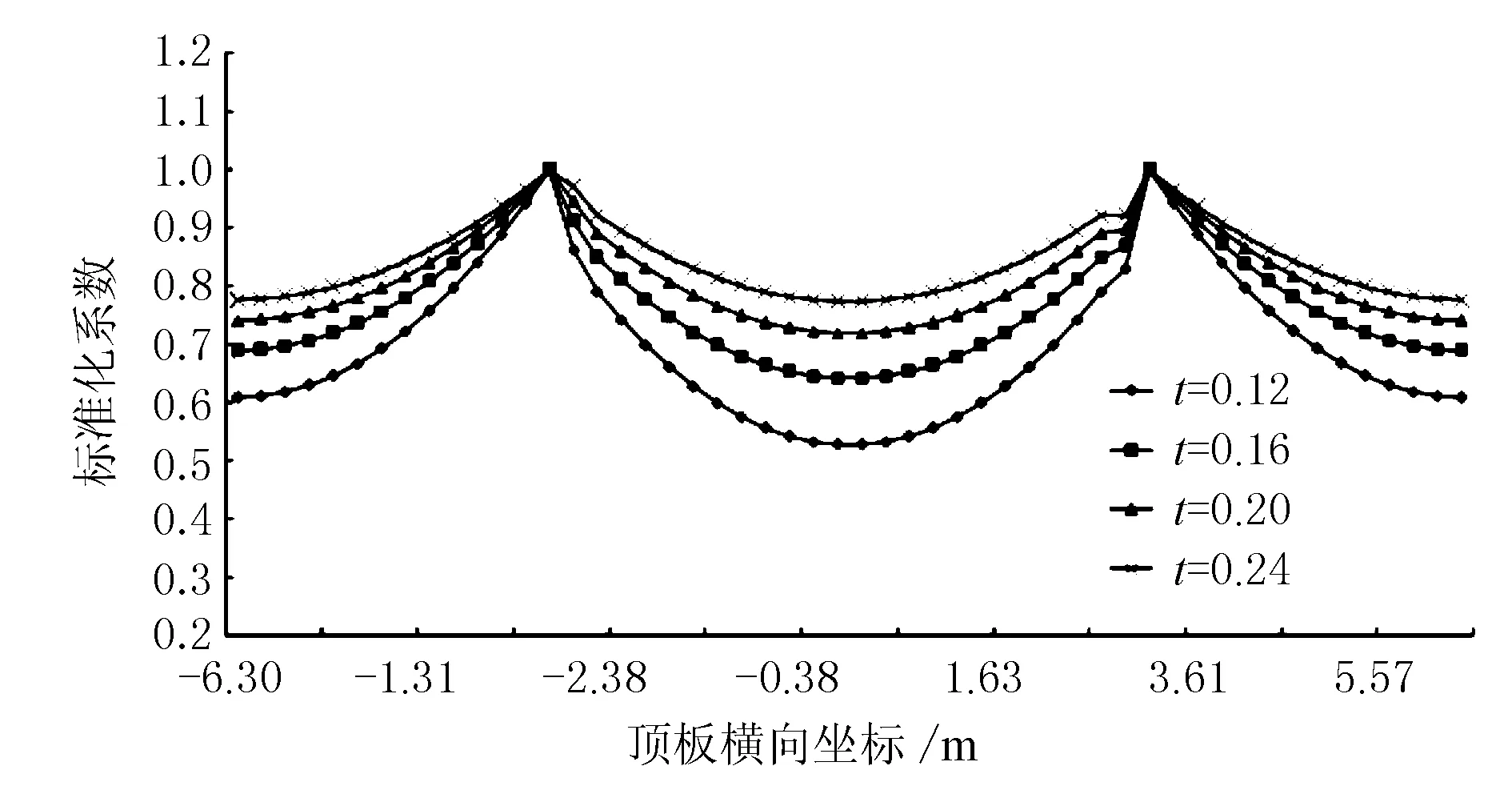
图8 顶板正应力标准化

图9 底板正应力标准化

由图8、图9可见，随着顶板厚度增加，顶板有效宽度系数从0.70增大到0.85，底板有效宽度系数保持1.0不变。增大顶板厚度不但可以有效降低顶板正应力，而且可以减小剪力滞效应，使得截面应力水平更均匀。

4 有效宽度计算结果对比

由1.2中规范公式及表格计算出模型有效宽度，并将3.1中各种情况下顶、底板的有效宽度列于表2。

表2 有效宽度比较

在3.1讨论的3种荷载工况下，自重、二期恒载、ZK活载在跨中产生的弯矩比值约为1.3∶1.0∶1.6，按此比例加权平均求得的顶、底板有效宽度系数分别为0.88和0.98。与2种规范对比发现RPC箱梁顶板的有效宽度较规范计算偏小11%，而底板有效宽度基本吻合《混凝土规范》。

5 结论

1) 箱梁自重、二期恒载、ZK活载3种荷载工况下，二期恒载作用下剪力滞效应最为显著。

2) 随着梁高增加，跨中断面剪力滞效应逐渐增大。但由于实际工程中众多因素的控制，梁高取值变化幅度较小，认为梁高变化对跨中断面剪力滞效应的影响可忽略不计。

3) 增加顶板厚度可减小顶板剪力滞效应且有效减小压应力。

4) RPC箱梁顶板有效宽度较规范计算偏小，按现行规范设计偏不安全。

5) 降低二期恒载可以改善顶板有效宽度折减。

综上所述，RPC箱梁在剪力滞效应方面较常规混凝土箱梁有所差异，现行规范对有效宽度的计算在RPC箱梁中能否直接应用需要进一步深入研究。