考虑土层剪切模量径向变化的锚杆受力变形特性分析*
2018-08-14梁冠亭肖开乾
梁冠亭 肖开乾 张 兵
(1.武汉市市政建设集团有限公司 武汉 430000; 2.湖北秭兴长江大桥建设开发有限公司 武汉 430023)
锚杆支护广泛应用在工程建设的高边坡和深基坑开挖支护中。常见的锚杆受力变形计算分析方法有规范法、荷载传递法[1]、剪切位移法[2]等,其中剪切位移法由于考虑锚杆周边土的变形,更符合锚杆的实际工作状况,在理论上更为精准严谨。但是,由于其涉及的计算参数较多,取值困难,因而未能够被广泛推广。在运用剪切位移法进行锚杆受力变形分析时,需应用到一个重要的计算参数,即土体剪切模量G,该参数在同一地层中是基本不变的,但随着锚杆的压力注浆施工,浆液对土体产生一系列的渗入、劈裂和压密作用[3-5],将会导致钻孔一定径向范围内土体的力学性质产生改变,土体剪切模量G也会随之改变,在靠近钻孔边缘出现一定的增长。
本文基于剪切位移法,考虑剪切模量G沿孔径径向呈常数、线性、指数、抛物线4种不同的大小分布模式,推导锚杆沿轴向方向的轴力、剪应力和位移的解析解,并结合实例分析比较其中的变化规律及演变趋势。
1 荷载传递方程的建立
建立计算模型见图1,锚杆长度为L,选取dz锚固微段作为研究对象,根据锚杆长度方向z截面上的轴力P(z)与应力、应变之间关系可得
(1)
式中:u(z)为锚杆z方向上的位移;r0为锚杆半径;Ea为锚固体弹性模量。
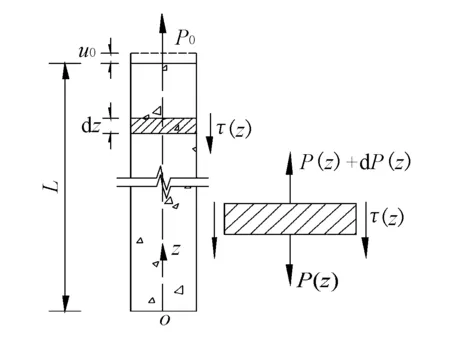
图1 计算模型简图
由锚固体单元沿轴向方向力的平衡方程得
dP(z)/dz-2πr0τ(z)=0
(2)
式中:τ(z)为锚杆z方向上的剪应力。
将式(1)代入式(2)得
d2u(z)/dz2-2τ(z)/r0Ea=0
(3)
为了能够反映锚杆锚固段周边土体的软化特性,界面剪应力与剪切位移之间的关系采用一次跌落模型,其中τf为峰值剪切强度,uf为τf对应的位移,τr为残余剪切强度,模型表达式为
(4)
式中:k为界面弹性剪切刚度;η为残余剪切强度与剪切峰值强度的比例系数。
2 锚固体弹塑性分析
2.1 弹性阶段
当锚杆的外荷载P0较小时,锚固段周边土体全部处于弹性阶段,由剪应力和剪切位移之间的关系可得
(5)
式中:rm为土体变形可以忽略不计的最大半径,一般取值为10倍r0;G(r)为土体剪切模量。
由于前述注浆效果对土体剪切模量产生的影响,剪切模量沿锚杆的径向分布是不均匀的,令
(6)
式中:ξ为土体剪切模量影响系数,具体的求解过程见本文第3节。
则由式(3)、式(4)和式(5)可得
d2u(z)/dz2-β2u(z)=0
(7)
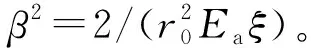
式(7)为二阶常微分方程,其通解为
u(z)=c11eβ z+c12e-β z
(8)
式中:c11,c12为微分方程待定系数。
根据锚杆的受力特点,可得其边界条件为
P|z=0=0,P|z=L=P0
(9)
可得
(10)
(11)
(12)
可得锚固段周边土体处于弹性阶段时锚杆全长的剪应力τ(z)分布表达式
(13)
2.2 塑性阶段
当锚杆继续向外拉拔,锚头的位移增大,靠近锚头的锚-土剪切界面开始出现塑性状态,且塑性区会随着拉拔荷载的增大继续发展。锚-土剪切界面分为弹性区和塑性区两部分,见图2,外荷载由此两部分可表示为
P0=Pe+Pp
(14)
式中:Pe为弹性区承担的外荷载;Pp为塑性区承担的外荷载。
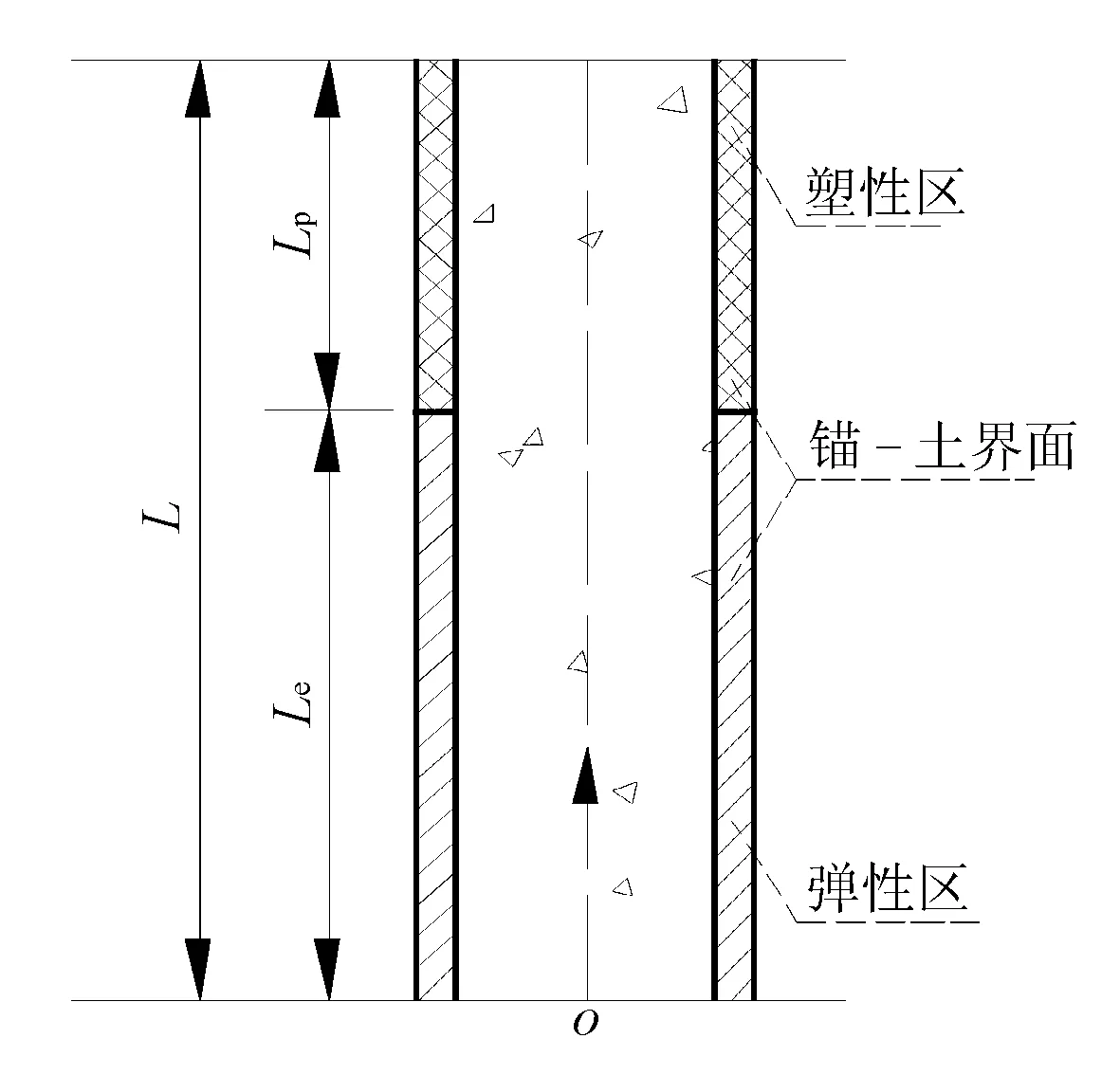
图2 锚土界面部分进入塑性状态
令式(11)中u(Le)=uf,可得Pe的表达式为
(15)
式中:Le为锚土界面的弹性区长度。
又因为锚土界面的塑性区的剪应力恒为剪切残余强度τr,故Pp的计算式可表示为
Pp=τrπD(L-Le)
(16)
对式(14)~(16)求解,采用迭代法即可求得Le。
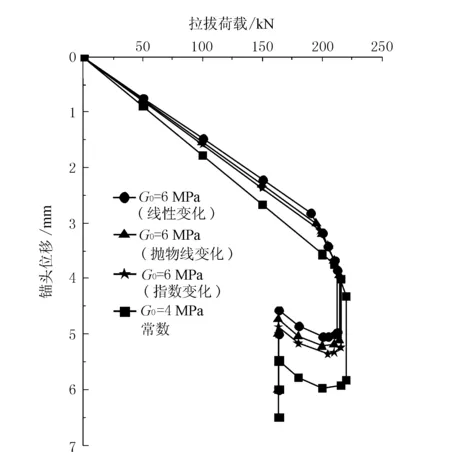
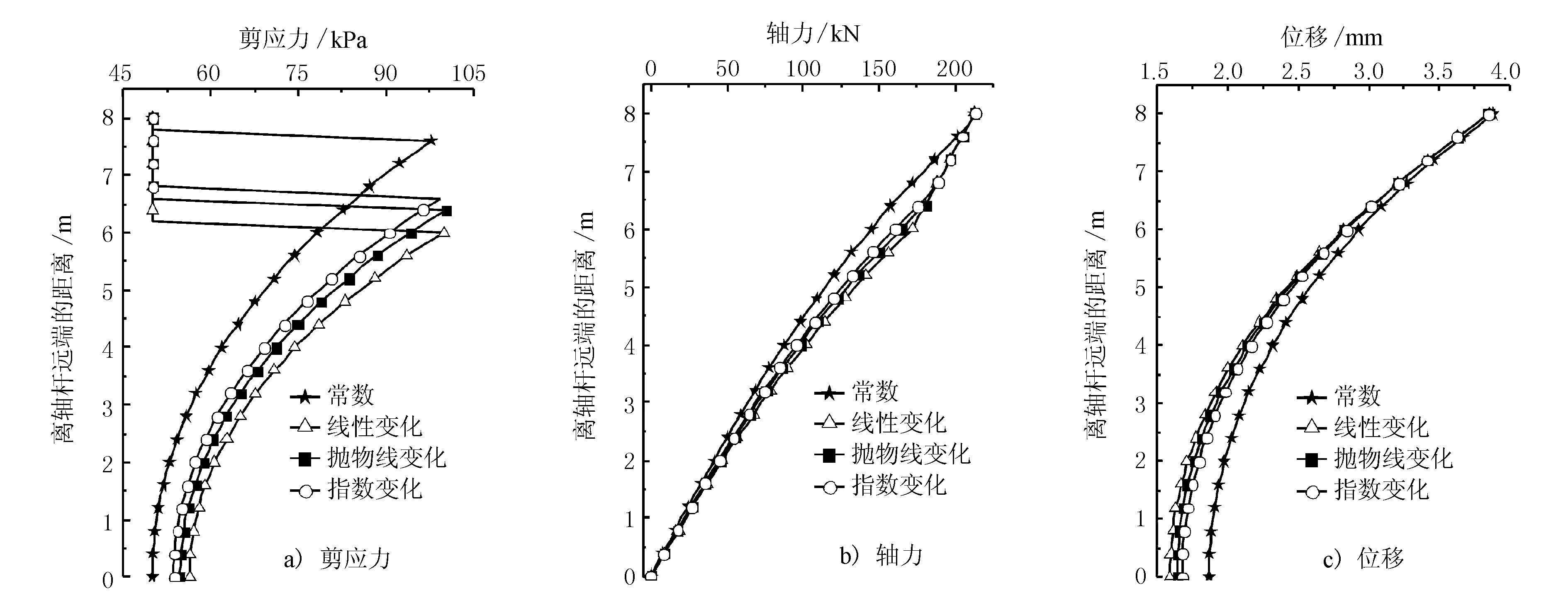
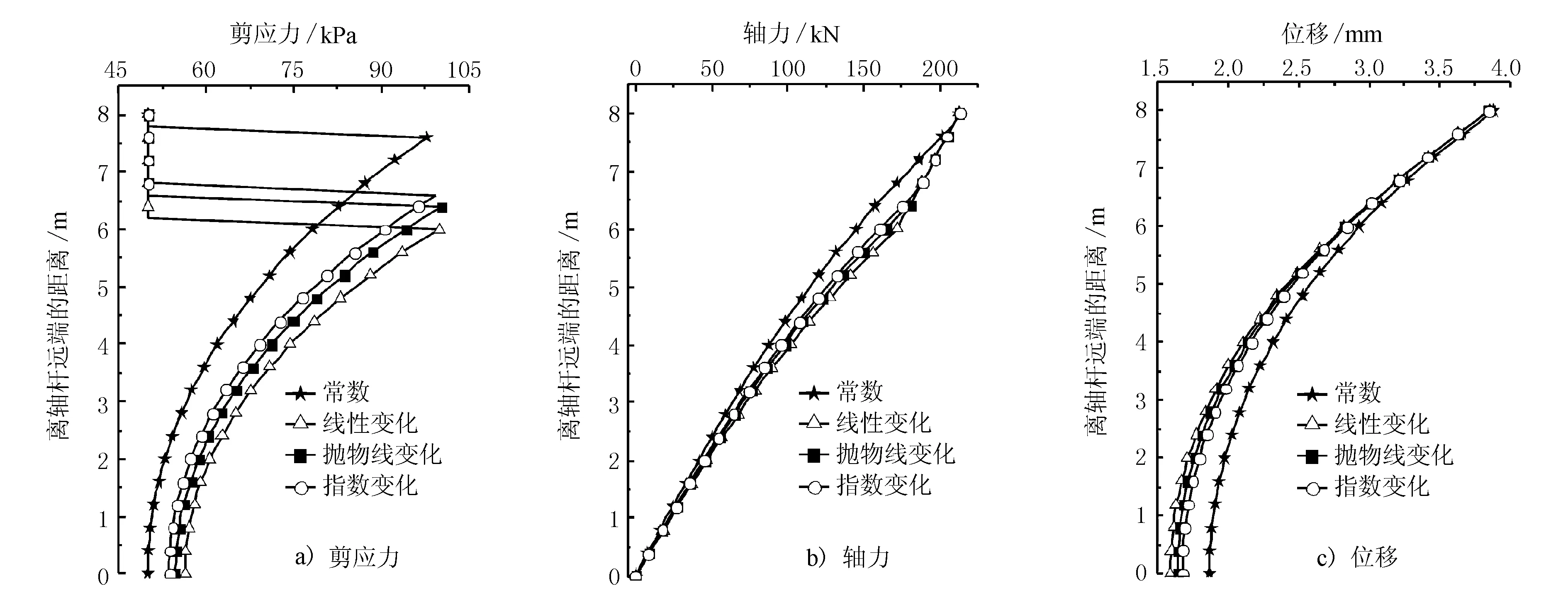
对于弹性区求解(即0 莽草酸分子中NBO分析的化学键二级微扰能数据列于表4,非常明显地C(4)C(5)的反键对分子构型有较大的影响,同时,含有O原子的键的二级微扰能均不少,表明碳碳双键、醇羟基、羧酸官能团是整个分子的核心. 而对于塑性区求解(即Le d2u(z)/dz2-2c1=0 (17) 式中:常系数c1=2τr/(r0Ea)。 由边界条件 P|z=L=P0,u|z=Le=uf (18) 可得塑性区位移表达式 u(z)=0.5c1z2+c2z+c3 (19) 至此,锚-土剪切界面进入弹塑性阶段后的位移u(z)表达式推导完毕,轴力P(z)、剪应力τ(z)表达式可参照本文第1部分求得。 从前述推导过程可知,锚杆的受力变形取决于如何求解式(7),不同的ξ值影响了整个锚杆的荷载-位移曲线发展规律。由于锚杆注浆的影响半径作用因素复杂,涉及到注浆压力、土体渗透系数、浆液初始黏度、注浆时间、浆液初凝时间和注浆高度等因素,而本文所关注的重点是注浆后锚杆钻孔径向范围内剪切模量的变化对锚杆受力变形的影响,在缺乏实测资料和相关已有成果的条件下,可作如图3所示的假定,注浆的影响半径与土体变形可以忽略不计的最大半径rm一致,即径向rm处土体的剪切模量与天然状态下土体的剪切模量一致,用符号Gm表示;而在锚杆和土体的交接界面r0处,土体的剪切模量由于注浆的影响可能发生改变,以符号G0表示;从G0到Gm的径向变化,假设为4种分布情况,即不考虑变化(常数)、线性变化、抛物线变化和指数变化。 图3 土体剪切模量沿径向的不同分布假设 当土体视为不受注浆作用影响时,其剪切模量与原状土的剪切模量一致,大小为Gm,可对式(6)进行直接积分求解,系数ξ0表达式为 ξ0=ln (rm/r0)/Gm (20) 如图3所示,若土体的剪切模量受注浆的影响,靠近锚杆处的剪切模量为G0,而径向远端处土体的剪切模量为Gm,且在锚杆的影响范围内,土体的剪切模量以线性形式变化分布,则土体剪切模量影响系数ξ1表达式可表示为 (21) 若土体的剪切模量以抛物线形式变化分布,其余条件如2.2,则其土体剪切模量影响系数ξ2表达式可为 (22) 若土体的剪切模量以指数形式变化分布,其余条件如2.2,则其土体剪切模量影响系数ξ3表达式可为 (23) 式中:B3=ln (G0/Gm)/(rm-r0);A3=G0/e-B3r0。 式(23)无法进行直接的积分运算求解,可通过数值分析软件进行简单的数值积分求得。 通过本节的理论推导,得到了土体剪切模量沿径向不同变化分布下,土体剪切模量影响系数ξ的不同表达式。至此,考虑土体剪切模量变化的锚杆受力变形特性理论分析体系建立完毕。 下文借助某算例,探讨由注浆等因素造成剪切模量沿径向变化从而导致锚杆受力变形所产生的差异。假设有一黏结锚杆长8 m,钻孔直径130 mm,锚杆受力的影响半径rm为钻孔半径r0的10倍,锚固体的的模量由杆体和胶凝体各自的模量按照面积加权平均计算取值为28.4 GPa,土体在天然状态下的剪切模量Gm为4.0 MPa,界面剪切模型服从一次跌落模型,峰值剪切强度τf为100 kPa,残余剪切强度τr为50 kPa。现考虑因注浆的渗入和劈裂等作用,界面处(r=r0)土体的剪切模量G0提高至6.0 MPa,注浆影响范围与锚杆受力影响范围一致,因此,rm处土体的剪切模量仍为Gm,假设在注浆的影响范围内,剪切模量沿径向的变化规律分别呈现为线性、抛物线和指数形式的衰减。 通过本文理论推导,分析锚杆的荷载-位移(P0-u0)曲线在这3种变化规律下的异同,见图4,同时将不考虑剪切模量沿径向变化所得的P0-u0也绘于图4中。 图4 剪切模量沿径向变化下的P0-u0曲线(Gm=4 MPa) 由图4可见,若考虑剪切模量因注浆有所提高并沿径向衰减,其峰值拉拔荷载P0f会小于不考虑剪切模量变化的情况,剪切模量变化最为剧烈的线性变化情况,其峰值拉拔荷载为213.2 kN,而不考虑剪切模量变化情况下的峰值拉拔荷载为220.7 kN,前者比后者小3.4%,这是由于剪切模量的提高,根据式(5)不难发现界面峰值剪切强度对应的位移uf会变小,造成锚杆剪应力的发挥程度会降低,若本算例假设uf,则对应的τf会有所不同,这是由剪切位移法自身的特点所决定的。而锚杆的残余拉拔荷载P0r在各种情况下完全一致均为163.4 kN,这是因为在位移足够大时,剪切界面每一点处的剪应力为恒定的残余剪切强度。至于锚杆锚头的位移情况,在同一拉拔荷载水平下(如200 kN),考虑剪切模量线性变化情况下的锚头位移和不考虑剪切模量变化下的锚头位移分别为3.18 mm和3.56 mm,前者比后者小10.7%,同时对于各曲线刚出现峰值拉拔荷载时对应的锚头位移u0f,考虑剪切模量线性变化的情况u0f为3.85 mm,而不考虑剪切模量变化的情况u0f为4.32 mm,前者比后者小10.9%。 由图4可见,在峰值拉拔荷载附近,1个确定的拉拔荷载会对应2个不同的锚头位移,这是由于当锚土界面进入塑性状态时拉拔荷载降低所导致的必然现象。 图5~6绘出了同一拉拔荷载水平下不同阶段所对应的锚杆受力变形指标分布图。 图5 锚杆部分进入塑性状态的受力变形指标分布图(Q0=213 kN,弹性段>塑性段) 从图5a)可知,此时锚杆在靠近锚头的一段已经进入塑性状态,但塑性段的长度小于弹性段的长度,由于各种情况下的界面残余强度一致,因此,塑性段的剪应力均一致,只是考虑剪切模量线性变化情况下的锚杆塑性段最长,剪切模量分别以抛物线变化、指数变化和常数变化情况下锚杆塑性段长度将依次减小。而弹性段同一深度处的剪应力情况,不考虑剪切模量变化对应的大小小于考虑剪切模量变化对应的大小。从图5b)可知,不同剪切模量分布情况下的轴力分布曲线大致为直线型,但在弹性段和塑性段的分界点有一定的差异,这是由于该处剪应力的急剧变化所导致的。从图5c)可知,不同剪切模量分布情况下的锚杆在锚头处的位移一致,但在锚杆远端处,不考虑剪切模量变化情况下的位移大于考虑剪切模量变化情况下的位移。由于假定剪切模量分别为线性、抛物线和指数形式时曲线变化不大,因此对应的锚杆位移、轴力和剪应力分布曲线差异很小。 图6 锚杆部分进入塑性状态的受力变形指标分布图(Q0=213 kN,弹性段<塑性段) 图6为对应Q0等于213 kN时另一种情况的锚杆受力变形指标分布图,此时锚杆的塑性段已逐渐向锚杆远端发展,塑性段的长度大于弹性段的长度,剪切模量分别按照线性、抛物线和指数形式变化时,所得到的塑性段长度差别已小于0.2 m,因此在图6a)中表现为塑性段长度完全一致,而不考虑剪切模量变化情况下的塑性段长度也仅略大于考虑剪切模量变化的情况,此阶段各种情况下的弹塑段长度可认为已基本一样。对于锚杆的轴力分布,不同剪切模量分布情况对于轴力分布曲线已影响不大,轴力分布曲线基本上由2段直线组成,在弹性段和塑性段的分界处有1处转折,如图6b)所示。从图6c)还可知,不同剪切模量分布情况下对应的锚杆位移曲线关系大致为平行的曲线,不考虑剪切模量变化的情况与考虑剪切模量变化的情况有较大的差异,而剪切模量分别按照线性、抛物线和指数形式变化时,其相应的锚杆位移曲线差异较小。 本文基于剪切位移法,考虑注浆作用对周边土体的加固效应及其导致土体剪切模量提高的状况,假定提高后的土体剪切模量以线性、抛物线和指数3种分布方式沿径向衰减至土体自然状态下的剪切模量,建立了考虑剪切模量径向变化的锚杆受力变形分析理论,分析计算表明剪切模量的提高对锚杆峰值拉拔荷载影响不大,而残余拉拔荷载完全相同,但锚头的拔出位移量有一定的减小。工程上可考虑这一有利因素,在准确获取锚杆周边土层径向剪切模量的前提下,减少采用锚杆支护方式的高边坡和深基坑位移量,保证建筑物的安全。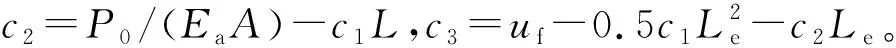
3 土体剪切模量沿径向不同变化分布的影响
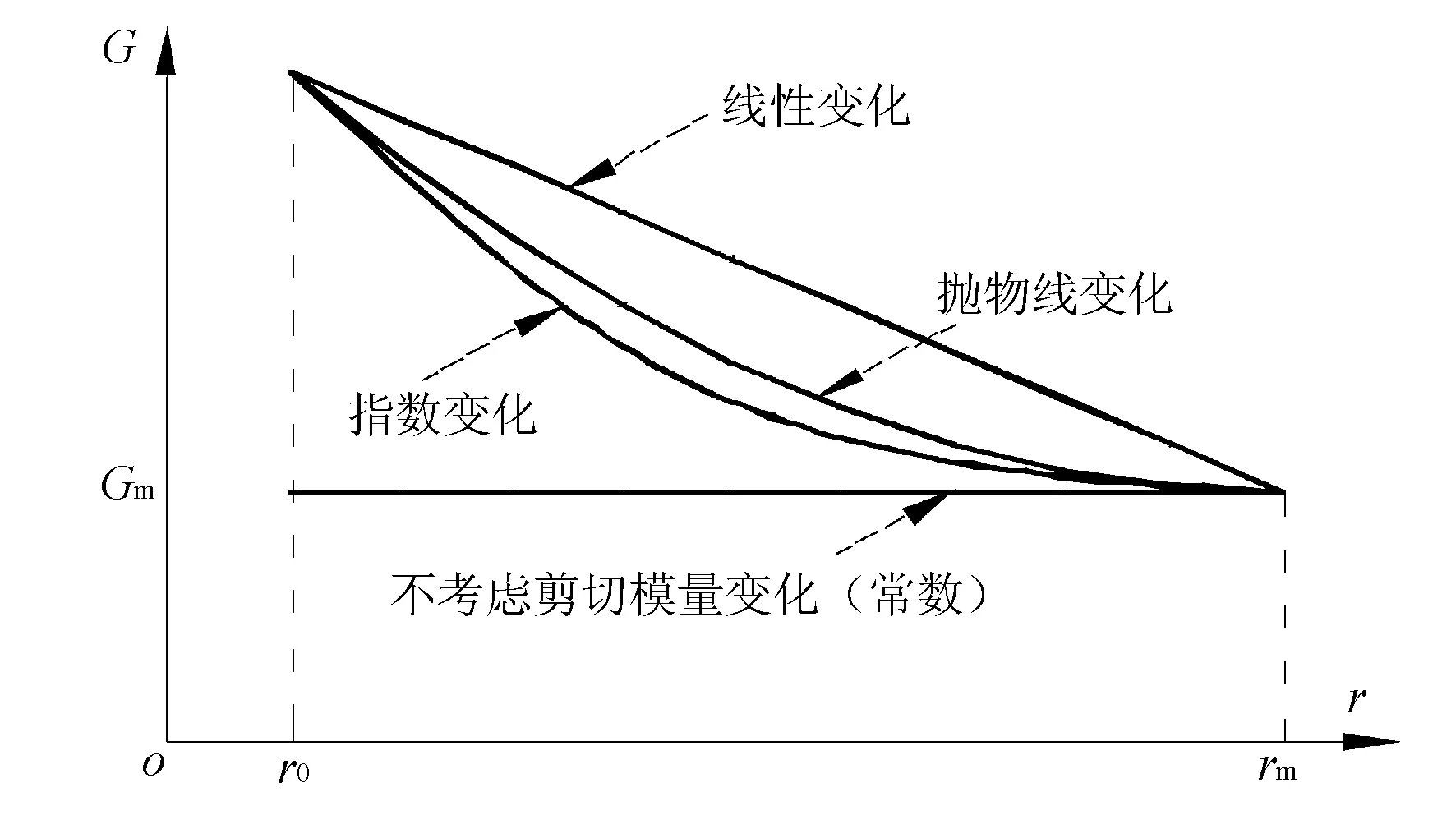
3.1 土体剪切模量沿径向不变
3.2 土体剪切模量沿径向以线性形式变化分布
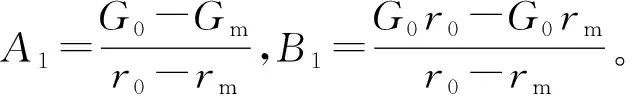
3.3 土体剪切模量沿径向以抛物线形式变化分布
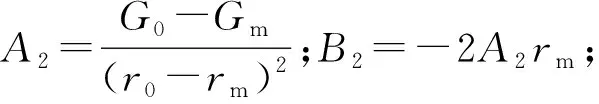
3.4 土体剪切模量沿径向以指数形式变化分布
4 算例分析与讨论
5 结语
