铁路路基承载力与路堤稳定性及沉降关系的探讨

毛晓辉

(中铁十五局集团第一工程有限公司 西安 710000)

在铁路路基的设计过程中，最为重要的3个控制指标参数分别是：地基承载力、稳定性及基础沉降[1]。为保证工程项目的安全性，确保铁路运输的畅通高效，这3个参数在工程建设中必须满足相关要求。

目前，我国已颁布的公路、铁路相关规范，明确了路堤稳定性、工后沉降要求，与其相比，路基承载力的规定则较为宽泛。其中，在行的铁路规范中，《铁路工程地基处理技术规程》 《铁路路基设计规范》等在规定条款上存在一定差异[2]。并且在我国铁路工程的学术研究中，有关铁路路基承载力与路堤稳定性及基础沉降之间关系的研究成果相对较少，与美国、日本等其他国家还存在差距。

在铁路路基设计中，基底承载力验算与否需要认真探讨，工程师有各自的见解。从设计角度来说，承载力验算是保证基础稳定的先决条件，而对铁路工程造价而言，承载力验算结果也有间接影响。在实际工程中，不同工程师根据经验在承载力与路堤稳定性的关系上有着相反的观点，部分人认为，路堤稳定性与沉降是重要因素，地基承载力验算与否取决于路堤稳定性与沉降是否满足工程实际的要求，若路堤稳定性与沉降均满足工程要求时，便可不验算地基承载力；某些工程师认为路基承载力若不满足要求，稳定性和沉降是否满足要求则无法保证，即路基承载力与路堤稳定性和沉降是充分条件关系，因此必须进行路基承载力验算。

基于上述问题，本文以国内铁路路基承载力规范规定为基础，根据地质勘查数据和相关规范，计算铁路荷载作用下的铁路路基承载力，研究路基承载力、路堤稳定性及基础沉降3者关系，以此讨论路基承载力验算结果是否影响路堤稳定与沉降。

1 铁路路基承载力要求及计算

1.1 铁路路基承载力要求

在我国当前铁路路基设计规范中，对铁路路基承载力有不同的要求。例如在TB 10001-2016 《铁路路基设计规范》[3]中，路基承载力要求应按照具体地质条件确定；在TB 10106-2010 《铁路工程地基处理技术规程》[4]中针对处理后的地基，其承载力需满足第3.3.2条文要求，即复合地基处理后的地基承载力应满足

pk≤k[σ]

(1)

式中：pk为基底压力，kPa；[σ]为处理后的地基容许承载力，kPa；k为地基承载力计算修正系数，对于路堤、场坪等柔性基础地基可取1.2～1.5。按上述要求，处理后的地基容许承载力应满足

[σ]≥pk/k=(0.66～0.83)pk

(2)

1.2 铁路路基承载力计算

由于对路基承载力计算的研究成果较多[5]，本文依据设计常用准则，对地基承载力可以采用太沙基承载力计算公式。其计算式为

Fu=c·Nc+q·Nq+1/2·γ·B·Nγ

(3)

式中：c为土的黏聚力，kPa；q为基础侧面超载，kPa；γ为土的容重，kN/m3；B为路基宽度，m；Nc，Nq，Nγ为承载力系数。

2 工程背景

潜江铁路支线地处湖北，位于江汉平原腹地，属于江汉平原货运系统的重要组成部分。线路全长36.952 km，路基全长27.824 km，占全线长度75.03%。在铁路路基设计中，路基横断面设计采用三角形路拱，由路基中心线向两侧设置坡度为4%的人字排水坡，利于雨水排出，以免浸泡路基面降低其强度。当铁路设计曲线需要加宽时，加宽段路基面的形状仍保持三角形不变。路堤标准横断面见图1。

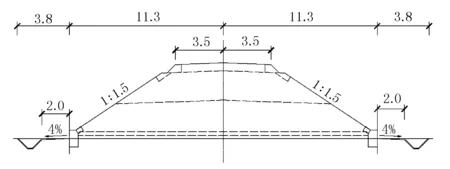
图1 路堤标准横断面(单位：m)

下面以潜江铁路支线工程为实例，通过具体计算以分析本工程内影响路基承载力的因素，并探讨其与路堤稳定性及沉降的关系。

3 路堤稳定性与路基基底承载力的关联

路堤稳定性分析由路堤堤身稳定性分析、路基和地基整体稳定性分析、路基沿斜坡地基或软弱层带滑动的稳定性分析3部分组成。影响路堤稳定性的因素多且复杂，无法在稳定性计算中完全考虑到。因此对于稳定性计算结果，还应结合场地条件和工程地质类比法进行判断以综合分析评价。较为常用的分析方法主要为简化Bishop法和瑞典条分法[6]。

图2是瑞典条分法简图。

图2 瑞典条分法简图

假定圆柱面为土体的滑动面，截面形状为圆弧，将滑动面以上土体视为刚体，并以它为脱离体进行分析，不考虑土条之间侧面上的相互作用，稳定系数计算公式为

(4)

式中：ci为第i个土条的黏聚力，kPa；φi为第i个土条的内摩擦角，(°)；li为第i个土条的滑弧长度，m；αi为第i个土条的坡角，(°)；Wi=γibihi，其中：γi为第i个土条的重度，kN/m3；bi，hi为宽度及高度，m。

以潜江铁路支线工程为背景，选取典型横断面进行分析，根据工程情况，假定路堤填料及路基基底地基土的黏聚力c值、内摩擦角φ和重度γ数值相同，以此分析路基在不同填土高度(3，5，8 m)时路基承载力情况，并分析其与路堤稳定性之间存在的关系。

定义路基承载力与路基高度相关的参数λ如下

λ=γH/Fu

(5)

式中：γ为填料容重，kN/m3；H为路堤高度，m。

在相同参数下，通过有关数据的计算和分析整理，得出λ与路堤稳定系数F的关系，见表1。

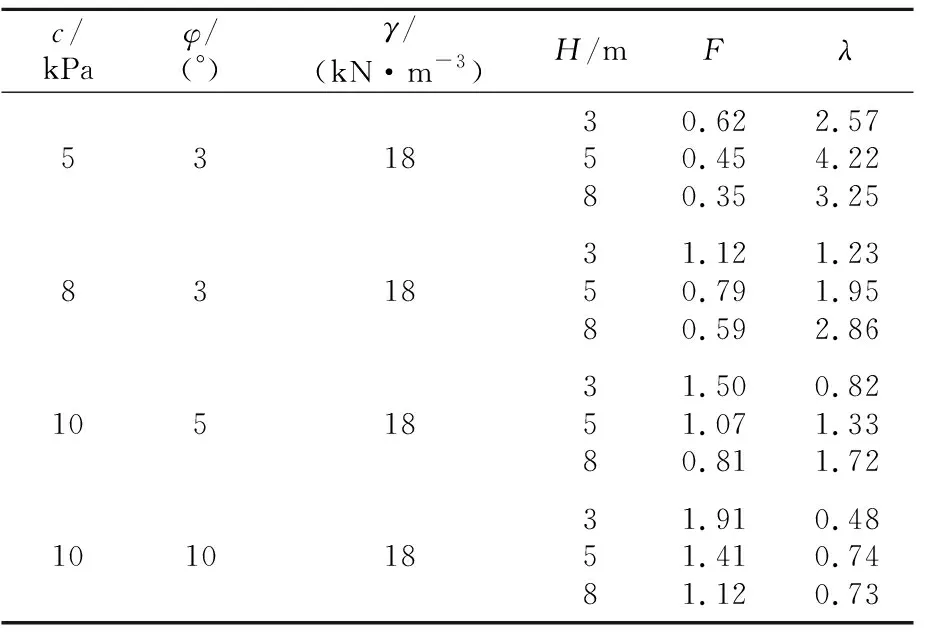
表1 λ与路堤稳定系数F计算表

由表1可见：①当λ逐渐增大，路堤稳定系数F逐渐减小，两者存在很好的相关性；②当λ>1时，此时基底承载力不满足要求且并未发生失稳，路堤仍可能处于稳定状态(F>1)。而在实际中，当作用在路堤的荷载大于地基所能承受的极限承载力时，地基将会遭到严重的剪切破坏进而产生失稳破坏。

从上述结果对比得知，当作用在路堤的荷载大于地基所能承受的极限承载力时，此时采用瑞典条分法分析的结果为路堤仍处于稳定状态，与采用承载力计算方法的路堤稳定性结果不一致，表明瑞典条分法得出的结果偏于不安全。而瑞典条分法和简化Bishop法相比，前者更偏于安全。基于上述原因，采用简化Bishop法验算路堤稳定性满足规范要求的情况下，并不能保证路堤仍会处于稳定状态而不发生失稳破坏。

根据潜江铁路支线工程计算结果可知，地基承载力与路堤稳定性无直接关联。该段路基承载力满足安全要求的前提是土条内摩擦角为5°时，堤高度不小于5 m或土条内摩擦角为10°；而稳定性满足要求则相对要宽泛的多。这主要是进行地基承载力验算时，假定条件与实际情况产生一定差异。当路堤的荷载大于地基极限承载力时，路堤仍可能保持稳定状态，并未发生失稳，因此，地基承载力验算是进行路堤设计时必不可少的重要环节。

4 路堤沉降与路基基底承载力的关联

路堤沉降主要由路堤填筑部分沉降和地基沉降2部分组成。地基在长期荷载作用下产生的最终沉降量可分为3个部分：瞬时沉降、主固结沉降及次固结沉降。次固结沉降是指地基在长期荷载作用下土体中有效应力不变，超孔隙水压力已完全消散的情况下，由土体骨架缓慢蠕变所产生的沉降。瞬时沉降是指施加荷载后，土体在很短的时间内产生的沉降。在实际工程的计算中，次固结沉降和瞬时沉降往往利用主固结沉降乘以修正系数m得出。根据压缩实验得到计算参数，主固结沉降Sc在计算沉降时应采用分层总和法进行计算。

当采用e-p曲线作为参数进行计算时，主固结沉降的沉降量Sc计算式为

(6)

式中：n为压缩土层内土层分层的数目；e1i为地基中各分层在自重应力作用下的稳定孔隙比；e2i为地基中各分层在自重应力和附加应力共同作用下的稳定孔隙比；hi为地基中各分层的初始厚度，m。

总沉降的计算公式为

S=mSc

(7)

式中：m为综合经验修正系数。

式(6)中的参数e-p曲线是在有侧向限制的条件下通过压缩试验得到的，由于存在侧向限制，式(6)计算得到的主固结沉降中，地基侧向变形产生沉降可以忽略不计。虽然式(7)在计算总沉降时侧向变形产生的沉降通过综合经验修正系数考虑了，但地基不发生破坏是式(7)适用的前提条件。据目前的研究可知，当作用在路堤的荷载大于地基所能承受的极限承载力时，地基将产生较大的侧向变形[7-8]。当作用上部荷载大于地基的极限承载力时，地基有可能发生失稳破坏，因此，计算路基的沉降时式(7)将不再适用。所以考虑地基侧向变形时，只有地基承载力满足实际要求时，地基沉降计算公式才能适用；否则，计算出的地基沉降也不准确。

根据上述适用原则，倘若采用式(7)进行沉降计算得到的结果满足设计要求，而地基侧向变形过大、地基破坏等情况也可能会发生，因此，在进行路堤沉降前应对地基极限承载力进行验算。只有当地基承载力验算满足规范要求时，才能科学、准确地判定路堤沉降计算结果。

5 结论

1) 当作用在路堤的荷载大于地基所能承受的极限承载力时，此时采用瑞典条分法计算的结果为路堤仍处于稳定状态，路堤稳定性结果在采用承载力计算和瑞典条分法分析时不一致，应分别计算路堤稳定性与地基承载力，以满足设计要求。

2) 只有地基承载力满足实际要求时，地基沉降计算公式才能适用，地基极限承载力满足实际要求是路堤沉降计算公式适用的前提。

3) 保证路堤稳定性及减小路堤沉降的前提条件是基底承载力满足设计要求，在路基设计中对路基基底承载力进行验算是必不可少的。